
第八章机械优化设计实例 第一节应用技巧 一、机械优化设计的一般过程 机械设计的全过程一般可分为: 1.建立优化设计的数学模型。 2.选择适当的优化方法。 3.编写计算机程序。 4.准备必须的初始数据并上机计算。 5.对计算机求得的结果进行必要的分析
第八章机械优化设计实例 第一节应用技巧 一、机械优化设计的一般过程 机械设计的全过程一般可分为: 1.建立优化设计的数学模型。 2.选择适当的优化方法。 3.编写计算机程序。 4.准备必须的初始数据并上机计算。 5.对计算机求得的结果进行必要的分析

二、建立数学模型的基本原则 数学模型的建立要求确切、简洁的反映工程问题的客 观实际。 数学模型的三要素:设计变量、目标函数、约束条件。 1.设计变量的选择 在充分了解设计要求的基础上,应根据各设计参数 对目标函数的影响程度分析其主次,应尽量减少设计 变量的数目,以简化优化设计问题。 应注意各设计变量应相互独立,否则会使目标函数 出现“山脊”或“沟谷”,给优化带来困难
二、建立数学模型的基本原则 数学模型的建立要求确切、简洁的反映工程问题的客 观实际。 数学模型的三要素:设计变量、目标函数、约束条件。 1.设计变量的选择 在充分了解设计要求的基础上,应根据各设计参数 对目标函数的影响程度分析其主次,应尽量减少设计 变量的数目,以简化优化设计问题。 应注意各设计变量应相互独立,否则会使目标函数 出现“山脊”或“沟谷”,给优化带来困难

3.约束条件的确定 2.目标函数的确定 把最重要的指标作为目标函数,其余的次要的指标可 作为约束条件。 对于一般机械,可按重量最轻或体积最小的要求建立目标函数; 对应力集中现象尤其突出的构件,则以应力集中系数最小为追 求的目标。 对于精密仪器,应按其精度最高或误差最小的要求建立目标函 数。 约束条件是就工程设计本身而提出的对设计变量取值 范围的限制条件
3.约束条件的确定 2.目标函数的确定 把最重要的指标作为目标函数,其余的次要的指标可 作为约束条件。 对于一般机械,可按重量最轻或体积最小的要求建立目标函数; 对应力集中现象尤其突出的构件,则以应力集中系数最小为追 求的目标。 对于精密仪器,应按其精度最高或误差最小的要求建立目标函 数。 约束条件是就工程设计本身而提出的对设计变量取值 范围的限制条件
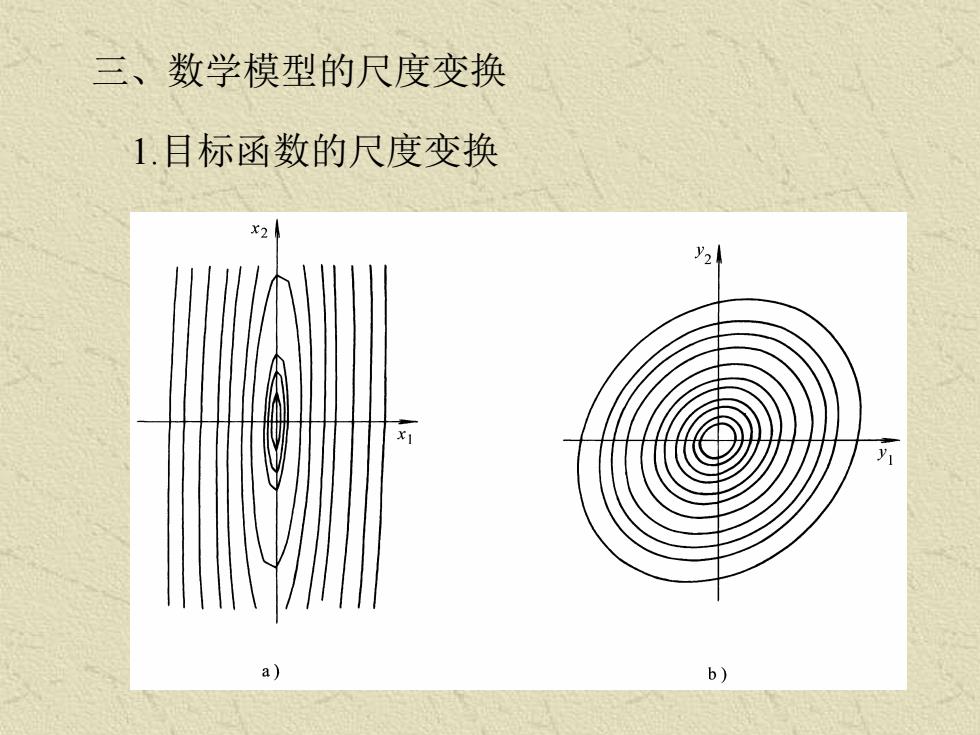
三、数学模型的尺度变换 1.目标函数的尺度变换
三、数学模型的尺度变换 1.目标函数的尺度变换

2.设计变量的尺度变换 当各设计变量之间在量级上相差很大时,在给定的搜索 方向上各自的灵敏度相差也很大。灵敏度大的搜索变化 快,灵敏度小的搜索变化慢。为了消除这种差别,可以 对设计变量进行重新标度。使它成为无量纲或规格化的 设计变量,这种处理称设计变量的尺度变换。 i i i y k x = 0 1/ i i k x = * * / i i i x y k =
2.设计变量的尺度变换 当各设计变量之间在量级上相差很大时,在给定的搜索 方向上各自的灵敏度相差也很大。灵敏度大的搜索变化 快,灵敏度小的搜索变化慢。为了消除这种差别,可以 对设计变量进行重新标度。使它成为无量纲或规格化的 设计变量,这种处理称设计变量的尺度变换。 i i i y k x = 0 1/ i i k x = * * / i i i x y k =

3.约束函数的规格化 约束函数的尺度变换称规格化。 由于各约束函数所表达的意义不同,使得各约束函数 值在量级上相差很大。 例如某热压机框架的优化设计中,许用应力为 [σ]= 150MPa,而下横梁的许用挠度[δ]=0.5mm,约束函数 为: ( ) ( ) 1 2 150 0 0.5 0 g x g x = − = −
3.约束函数的规格化 约束函数的尺度变换称规格化。 由于各约束函数所表达的意义不同,使得各约束函数 值在量级上相差很大。 例如某热压机框架的优化设计中,许用应力为 [σ]= 150MPa,而下横梁的许用挠度[δ]=0.5mm,约束函数 为: ( ) ( ) 1 2 150 0 0.5 0 g x g x = − = −

两者对数值变化的灵敏度相差很大,这对优化设计 是不利的。 例如采用惩罚函数时,两者在惩罚项中的作用相差 很大,灵敏度高的约束条件在极小化过程中首先得到 满足,而灵敏度小的几乎得不到考虑。 ( ) ( ) 1 2 / 1 0 / 1 0 g x g x = − = − 这样,各约束函数得取值范围都限制在[0,1]之 间,起到稳定搜索过程和加速收敛的作用
两者对数值变化的灵敏度相差很大,这对优化设计 是不利的。 例如采用惩罚函数时,两者在惩罚项中的作用相差 很大,灵敏度高的约束条件在极小化过程中首先得到 满足,而灵敏度小的几乎得不到考虑。 ( ) ( ) 1 2 / 1 0 / 1 0 g x g x = − = − 这样,各约束函数得取值范围都限制在[0,1]之 间,起到稳定搜索过程和加速收敛的作用
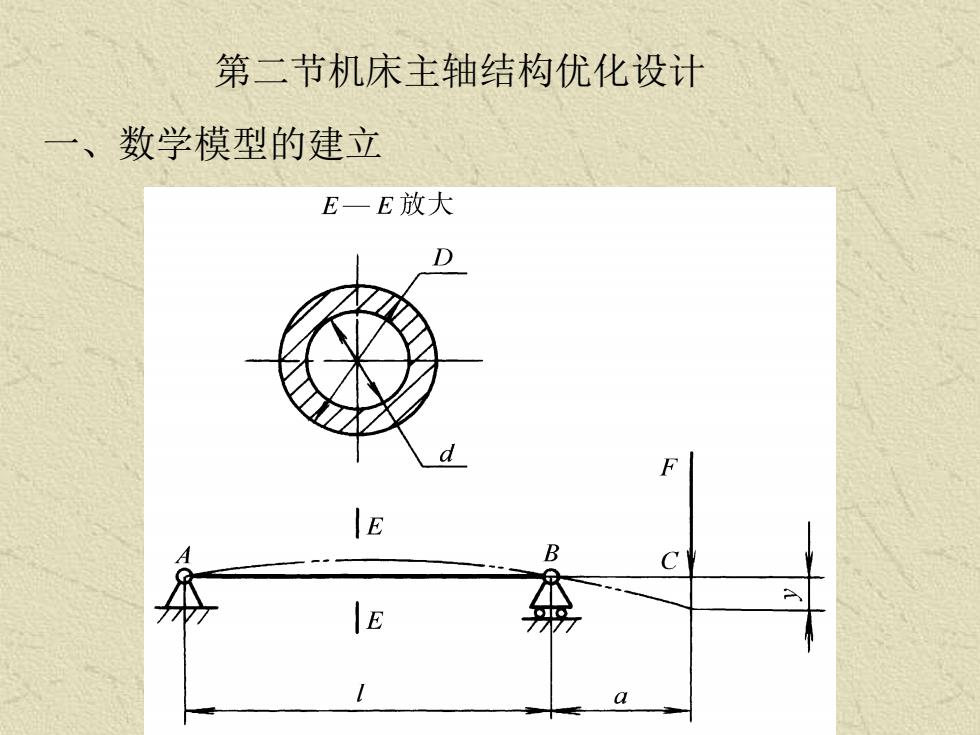
第二节机床主轴结构优化设计 一、数学模型的建立
第二节机床主轴结构优化设计 一、数学模型的建立

在设计这根主轴时,有两个重要因素需要考虑。一 是主轴的自重;一是主轴伸出端c点的挠度。 对于普通机床,不要求过高的加工精度,对机床主 轴的优化设计,以选取主轴的自重最轻为目标,外伸 端的挠度为约束条件。 当主轴的材料选定时,其设计方案由四个设计变量决 定。孔径d、外径D、跨距l及外伸端长度a。由于机床 主轴内孔用于通过待加工的棒料,其大小由机床型号 决定。不作为设计变量。故设计变量取为
在设计这根主轴时,有两个重要因素需要考虑。一 是主轴的自重;一是主轴伸出端c点的挠度。 对于普通机床,不要求过高的加工精度,对机床主 轴的优化设计,以选取主轴的自重最轻为目标,外伸 端的挠度为约束条件。 当主轴的材料选定时,其设计方案由四个设计变量决 定。孔径d、外径D、跨距l及外伸端长度a。由于机床 主轴内孔用于通过待加工的棒料,其大小由机床型号 决定。不作为设计变量。故设计变量取为

1 2 3 T T x x x x l da = = ( ) ( )( ) 2 2 1 3 2 1 4 f x x x x d = + − 机床主轴优化设计的目标函数为 再确定约束条件 ( ) 0 g x y y = − 0 在外力F给定的情况下,y是设计变量x的函数,其值按 下式计算 ( ) 2 3 Fa l a y I + =
1 2 3 T T x x x x l da = = ( ) ( )( ) 2 2 1 3 2 1 4 f x x x x d = + − 机床主轴优化设计的目标函数为 再确定约束条件 ( ) 0 g x y y = − 0 在外力F给定的情况下,y是设计变量x的函数,其值按 下式计算 ( ) 2 3 Fa l a y I + =