
第一章 机械优化设计概述 第一节 应用实例 机械优化设计问题来源于生产实际。 现在举典型实例来说明优化设计的基本问 题。 图1-1所示的人字架由两个钢管构成,其顶点受外力 2F=3× N。人字架的跨度2B=152cm,钢管壁厚T=0.25cm, 钢管材料的弹性模量E=2.1 × Mpa,材料密度ρ=7.8 × / ,许用压应力 = 420MPa。求在钢管压应力 不超过许用压应力 和失稳临界应力 的条件下,人字 架的高h和钢管平均直径D,使钢管总质量m为最小。 5 10 5 10 3 10 kg 3 m y y e
第一章 机械优化设计概述 第一节 应用实例 机械优化设计问题来源于生产实际。 现在举典型实例来说明优化设计的基本问 题。 图1-1所示的人字架由两个钢管构成,其顶点受外力 2F=3× N。人字架的跨度2B=152cm,钢管壁厚T=0.25cm, 钢管材料的弹性模量E=2.1 × Mpa,材料密度ρ=7.8 × / ,许用压应力 = 420MPa。求在钢管压应力 不超过许用压应力 和失稳临界应力 的条件下,人字 架的高h和钢管平均直径D,使钢管总质量m为最小。 5 10 5 10 3 10 kg 3 m y y e
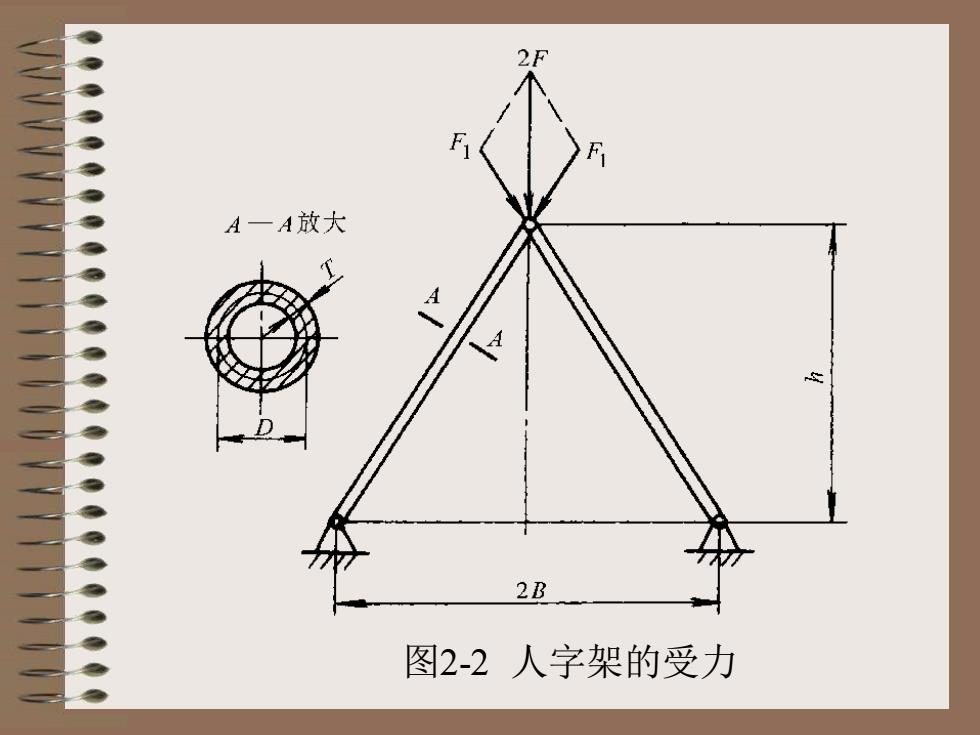
图2-2 人字架的受力
图2-2 人字架的受力

人字架的优化设计问题归结为: T x D H = 使结构质量 m x( ) → min 但应满足强度约束条件 ( ) y x 稳定约束条件 ( ) e x
人字架的优化设计问题归结为: T x D H = 使结构质量 m x( ) → min 但应满足强度约束条件 ( ) y x 稳定约束条件 ( ) e x

钢管所受的压力 1 2 2 2 1 FL F B h ( ) F h h + = = 失稳的临界力 2 e 2 EI F L = 钢管所受的压应力 ( ) 1 2 2 2 1 F F B h A TDh + = =
钢管所受的压力 1 2 2 2 1 FL F B h ( ) F h h + = = 失稳的临界力 2 e 2 EI F L = 钢管所受的压应力 ( ) 1 2 2 2 1 F F B h A TDh + = =

钢管的临界应力 ( ) ( ) 2 2 2 2 2 8 e e F E T D A B h + = = + 强度约束条件 ( ) y x 可以写成 ( ) 1 2 2 2 y F B h TDh + 稳定约束条件 ( ) e x 可以写成 ( ) ( ) ( ) 1 2 2 2 2 2 2 2 2 8 F B h E T D TDh B h + + +
钢管的临界应力 ( ) ( ) 2 2 2 2 2 8 e e F E T D A B h + = = + 强度约束条件 ( ) y x 可以写成 ( ) 1 2 2 2 y F B h TDh + 稳定约束条件 ( ) e x 可以写成 ( ) ( ) ( ) 1 2 2 2 2 2 2 2 2 8 F B h E T D TDh B h + + +

人字架的总质量 ( ) ( ) 1 2 2 2 m D h AL TD B h , 2 2 = = + 这个优化问题是以D和h为设计变量的二 维问题,且只有两个约束条件,可以用 解析法求解。 除了解析法外,还可以采用作图法求解
人字架的总质量 ( ) ( ) 1 2 2 2 m D h AL TD B h , 2 2 = = + 这个优化问题是以D和h为设计变量的二 维问题,且只有两个约束条件,可以用 解析法求解。 除了解析法外,还可以采用作图法求解
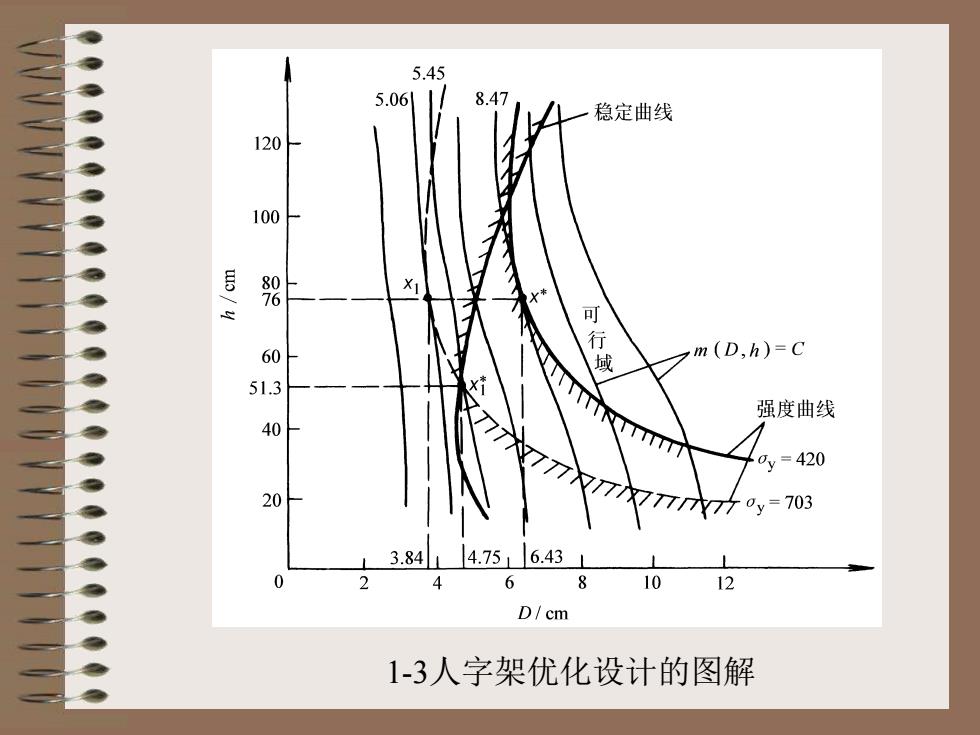
1-3人字架优化设计的图解
1-3人字架优化设计的图解

第三节优化设计问题的数学模型 一、设计变量 在优化设计的过程中,不断进行修改、调整, 一直处于变化的参数称为设计变量。 设计变量的全体实际上是一组变量,可用一 个列向量表示: 1 2 . T n x x x x =
第三节优化设计问题的数学模型 一、设计变量 在优化设计的过程中,不断进行修改、调整, 一直处于变化的参数称为设计变量。 设计变量的全体实际上是一组变量,可用一 个列向量表示: 1 2 . T n x x x x =

图2-4 设计空间
图2-4 设计空间

二、约束条件 一个可行设计必须满足某些设计限制条件, 这些限制条件称作约束条件,简称约束。 约束 性能约束 侧面约束 针对性能要求 只对设计变量的取值范 围限制(又称边界约束) (按性质分) 按数学表达形式分:
二、约束条件 一个可行设计必须满足某些设计限制条件, 这些限制条件称作约束条件,简称约束。 约束 性能约束 侧面约束 针对性能要求 只对设计变量的取值范 围限制(又称边界约束) (按性质分) 按数学表达形式分: