《金融投资学》教学资源（英文文献）Survivorship Bias in Performance Studies.pdf_大学文库

The Review of Financial Studies /v 5n 4 1992 on a risk-adjusted basis.While more recent evidencel qualifies this negative conclusion somewhat [Grinblatt and Titman (1989),Ippolito (1988)1,there is still no strong evidence that manager performance over and above the market indices can justify the fees managers charge and the commission costs they incur. The fact that managers as a group perform poorly does not preclude the possibility that particular managers have special skills.Given the high turnover of managers,it is conceivable that the market selects out those managers with skills.Skillful managers are those who suc- ceed and survive.It is this view,fostered by annual mutual fund performance reviews of the type published by Barrons,Business Week, Consumer Reports,and other publications,that leads to the popular investment strategy of selling shares in mutual funds that underper- form the average manager in any given year,and buying shares in those funds with superior performance.Despite the popular impres- sion that"hot hands"'exist among mutual funds,there has been very limited empirical evidence to address this issue. Past performance is usually a highly significant input into the deci- sion to hire or fire pension fund money managers.However,Kritzman (1983)reports that for fixed-income pension fund money managers retained for at least 10 years,there is no relationship either in returns or in relative rankings between the performance in the first five years and the second five years.In an unpublished portion of the same study,this finding also extended to equity managers.Similar results are found for institutional funds by Dunn and Theisen (1983)and for commodity funds by Elton,Gruber,and Rentzler (1990).2 In con- trast to these findings,Elton and Gruber(1989,p.602)conclude on the basis of a Securities and Exchange Commission (1971)study that mutual funds which outperform other funds in one period will tend to outperform them in a second.Grinblatt and Titman(1988)suggest that five-year risk-adjusted mutual fund returns do contain some pre- dictive power for subsequent returns.Lehmann and Modest report similar results for the period 1968-1982,but suggest that this finding is sensitive to the method used to compute risk-adjusted performance measures. On the basis of data for the period 1974-1988 both Hendricks, Patel,and Zeckhauser (1991)and Goetzmann and Ibbotson (1991) obtain far stronger results.The first study is limited to 165 equity Some of this evidence is controversial in nature.See Elton et al.(1993)for a discussion of the Ippolito findings :The commodity fund result applies to returns on funds.However,Elton,Gruber,and Rentzler (1990)find evidence of persistence in performance of different funds managed by the same general partner.It would be interesting to discover whether dispersion in risk across surviving managers would suffice to explain this result. 554

Survivorship Bias in Performance Studies funds for the period 1974-1988,while the latter study considers a much larger sample of 728 mutual funds for the period 1976-1988, 258 of which survived for the entire period.The major conclusions of the two studies are similar.Performance persists.3 While the experimental designs and data of these studies differ considerably,the generic results may be illustrated on Tables 1 and 2.The relationship between successive three-year growth equity fund risk-adjusted total returns for the period 1976-1987 is documented in Table 1.The 2 x 2 contingency tables show the frequency with which managers who performed in the top half of all managers [on a Jensen (1968)a risk-adjusted basis]for a given three-year interval also performed in the top half in the subsequent three-year interval. For every period studied,the results are similar.If a manager wins in the first three years,the probability is greater than 50 percent that the manager will win in the second three years.These results are also statistically significant in at least two of the three successive three- year intervals. Goetzmann and Ibbotson (1991)report contingency tables similar to those given in Table 1 for a variety of time periods and performance horizon intervals.The data on which Table 1 is based are similar to those of the Hendricks,Patel,and Zeckhauser (1991)study.An alter- native approach is to regress second-period Jensen's a's against first- period Jensen's a's.A significantly positive slope coefficient is evi- dence of persistence.The result of this exercise is presented in Table 2.The results correspond with those reported in Table 1.The evi- dence of persistence is strongest in the first and third subperiod of the data.Hendricks,Patel,and Zeckhauser (1991)suggest computing the returns on a self-financing portfolio strategy,a methodology they Note that the Kritzman (1983)and Dunn and Theisen (1983)results apply to pension fund money managers,while the other studies that indicate persistence all refer to mutual funds.Representatives from Frank Russell Company and other pension fund consulting companies indicate that efforts to replicate the mutual fund persistence results using pension fund data have to this date been unsuccessful.Part of the reason for this difference might be that mutual fund returns are measured after fees,while pension fund returns typically are measured before commissions (see note 6). One has to be a little careful interpreting the statistical significance of the x'values.The identi. fication of managers as winners or losers is actually ex post.For this reason,we expect to find the winners-following-winners result at least 50 percent of the time.This ex post conditioning also implies that the standard x2 tests (with or without the Yates 2 x 2 continuity correction)will be misspecified.Fortunately,an alternative statistic,the cross-product ratio (given as the ratio of the product of the principal diagonal cell counts to the product of the off-diagonal counts in the 2 x 2 table),has well-known statistical properties.Statisticians prefer the cross-product ratio (or mea- sures closely related to it)because it simultaneously provides a test of the hypothesis that the two classifications are independent,as well as giving a measure of the dependence (Bishop et al.(1975 p.373ff.)]In the present case,row and column,sums of each 2 x 2 contingency table are fixed because of ex post conditioning.Thus,the winner-winner cell count determines all other cell counts,and is distributed as the hypergeometric distribution conditional on row and column counts. Thus,the p-value of the cross-product ratio statistic is given by the sum of hypergeometric prob- abilities of cell counts at least as great as the observed winner-winner count [Agresti (1990,p.60)]. This is known as Fisher's exact test. 555

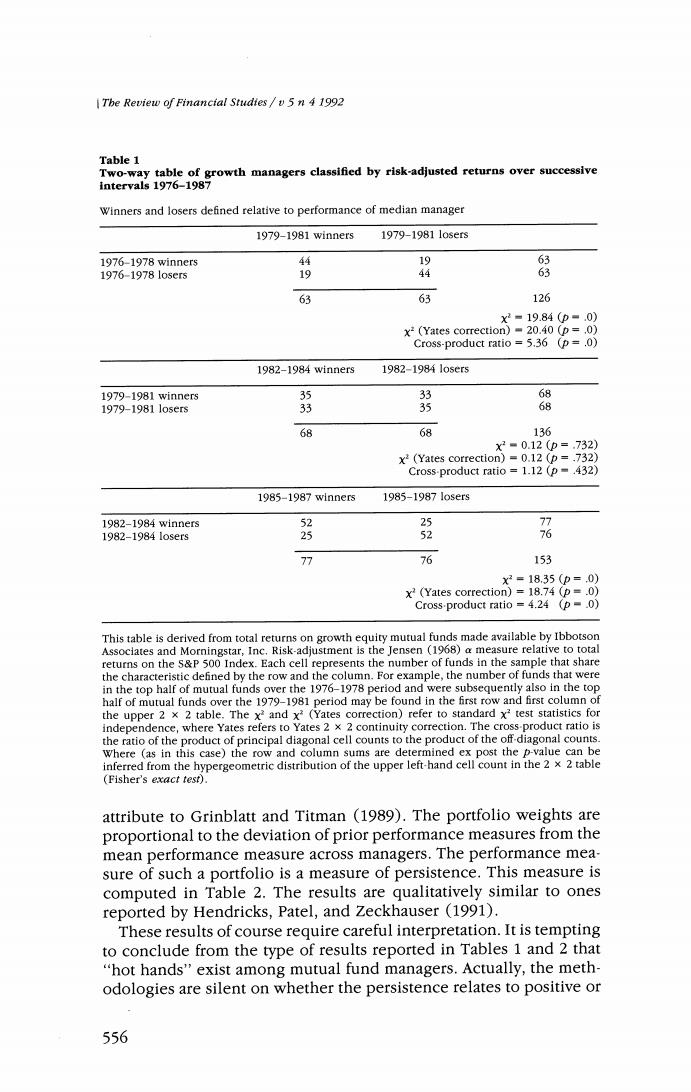
The Review of Financial Studtes/v 5n 4 1992 Table 1 Two-way table of growth managers classified by risk-adjusted returns over successive intervals 1976-1987 Winners and losers defined relative to performance of median manager 1979-1981 winners 1979-19811 osers 1976-1978 winner5 44 19 63 1976-1978105er5 19 63 63 126 X2=19.84(p=.0) x2(Yates correction)=20.40 (p=.0) Cross-product ratio 5.36 (p=.0) 1982-1984 winners 1982-19841o5er5 1979-1981 winners5 35 33 68 1979-19811o5er5 33 35 68 68 68 136 X2■0.12(p=.732) x2(Yates correction)=0.12 (p=.732) Cross-product ratio =1.12(p-.432) 1985-1987 winners 1985-19871 osers 1982-1984 winners 52 5 77 1982-19841 osers 25 52 76 77 76 153 x2=18.35(p=.0) x2(Yates correction)=18.74 (p=.0) Cross-product ratio =4.24 (p=.0) This table is derived from total returns on growth equity mutual funds made available by Ibbotson Associates and Morningstar,Inc.Risk-adjustment is the Jensen (1968)a measure relative to total returns on the s&P 500 Index.Each cell represents the number of funds in the sample that share the characteristic defined by the row and the column.For example,the number of funds that were in the top half of mutual funds over the 1976-1978 period and were subsequently also in the top half of mutual funds over the 1979-1981 period may be found in the first row and first column of the upper 2 x 2 table.The x2 and x?(Yates correction)refer to standard x?test statistics for independence,where Yates refers to Yates 2 x 2 continuity correction.The cross-product ratio is the ratio of the product of principal diagonal cell counts to the product of the off-diagonal counts. Where (as in this case)the row and column sums are determined ex post the p-value can be inferred from the hypergeometric distribution of the upper left-hand cell count in the 2 x 2 table (Fisher's exact test). attribute to Grinblatt and Titman (1989).The portfolio weights are proportional to the deviation of prior performance measures from the mean performance measure across managers.The performance mea- sure of such a portfolio is a measure of persistence.This measure is computed in Table 2.The results are qualitatively similar to ones reported by Hendricks,Patel,and Zeckhauser (1991). These results of course require careful interpretation.It is tempting to conclude from the type of results reported in Tables 1 and 2 that "hot hands"exist among mutual fund managers.Actually,the meth- odologies are silent on whether the persistence relates to positive or 556

Survivorsbip Bias in Performance Studies Table 2 Regression-based measures of persistence in performance,1976-1987 Cross-section regression approach' Period January 1976-December 1981: a2=,0885+.4134a1 (5.38)(6.47) R2=2.53;n=126 Period January 1979-December 1984: c1■-.0831+.0070a, (-3.69)(0.07) R2=.000:n=134 Period January 1982-December 1987: a=-.0753+.3052a, (-6.53)(5.28) R2=.156:n=153 Time-series self-financing portfolio approach? Period January 1977-December 1987: m=0018-.0078r (2.88)(-.61) 2=.003;n=132 (t-values in parentheses) Jensen's a is computed for the sample of funds described in Table 1 for each of four three-year subperiods of data starting in 1976-1978.Each panel reports results from the cross-section regres sion of performance measures on prior performance measures.The first panel gives results from the regression of Jensen's a measures estimated on the basis of data for the period January 1979- December 1981 on similar measures estimated for the period January 1976-December 1978. This corresponds to the measure employed by Hendricks,Patel,and Zeckhauser (1991)with four quarter evaluation and holding periods.For each year starting in 1976,Jensen's a measures are computed.The deviation of these measures from their mean corresponds to a self financing port- folio,which is then applied to excess returns on funds measured for the subsequent year.The portfolio is updated at the end of each year.The regression reports results from the time-series regression of the resulting monthly excess returns on market excess returns.The intercept corre- sponds to a performance measure for this portfolio strategy. negative performance.This is most readily apparent in Table 1 when we observe that the row and column sums are specified ex post given the sample of money managers.In other words,given the row and column sums and the"winner-winner"cell count,the"loser-loser" count is simply the residual.Given the "loser-loser'count,the "win- ner-winner"is the residual.When we measure risk-adjusted perfor- mance relative to zero (Table 3),we find that persistence can just as easily relate to negative performance as it does to positive perfor- mance.Sometimes (1976-1981)good performance is rewarded by subsequent good performance."Hot hands"are evident.Sometimes (1982-1987)it is the case that bad performance is punished by further bad news.This result is also apparent examining the intercepts of the cross-section regressions reported in Table 2.Results reported in Table 4 indicate that the persistence of poor performance serves to explain some but not all of the results reported in the previous tables. This table gives regression-based measures of persistence excluding those managers who experienced negative average Jensen's a for the 5571

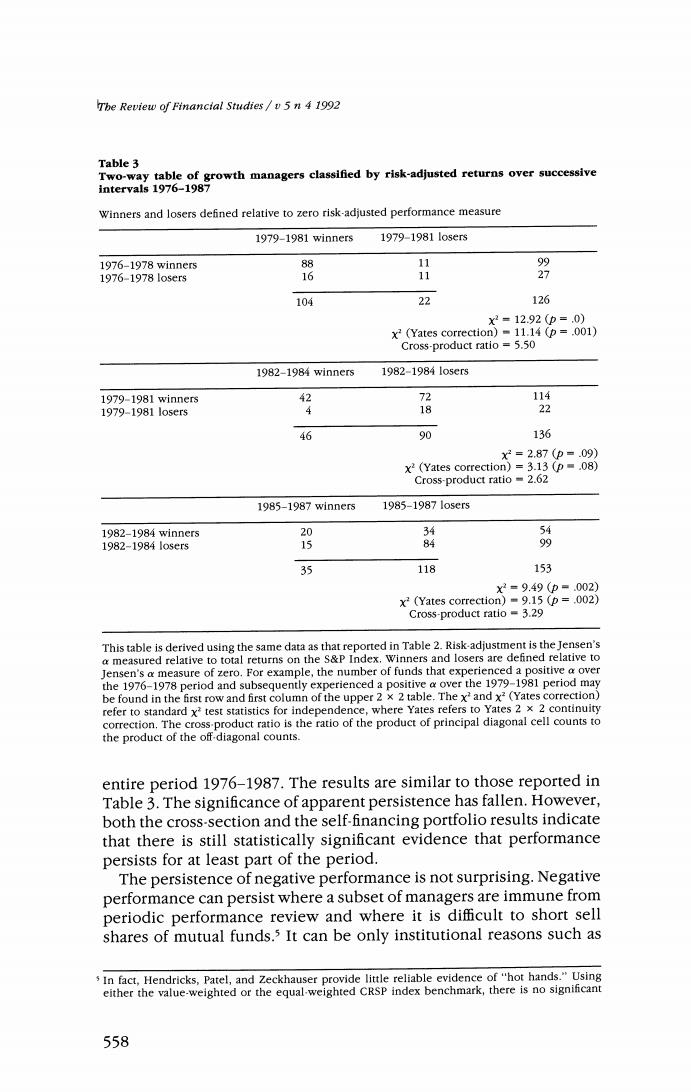
The Review of Financial Studies /v 5 n 4 1992 Table 3 Two-way table of growth managers classified by risk-adjusted returns over successive intervals 1976-1987 Winners and losers defined relative to zero risk-adjusted performance measure 1979-1981 winners 1979-19811o5ers 1976-1978 winner5 88 11 1976-1978lo5ers 16 11 27 104 22 126 x2=12.92(p=.0) x2 (Yates correction)=11.14 (p=.001) Cross-product ratio =5.50 1982-1984 winners 1982-19841o5er5 1979-1981 winners 2 72 114 1979-1981o5ers 18 22 46 90 136 xX2=2.87(p-.09) x2(Yates correction)=3.13 (p=.08) Cross-product ratio 2.62 1985-1987 winners 1985-19871osr5 1982-1984 winners 20 4 河 1982-19841o5er5 15 84 35 118 153 x2=9.49(p=.002) x2 (Yates correction)=9.15(p=.002) Cross-product ratio -3.29 This table is derived using the same data as that reported in Table 2.Risk-adjustment is the Jensen's a measured relative to total returns on the S&P Index.Winners and losers are defined relative to Jensen's a measure of zero.For example,the number of funds that experienced a positive a over the 1976-1978 period and subsequently experienced a positive a over the 1979-1981 period may be found in the first row and first column of the upper 2 x 2 table.The x'and x2(Yates correction) refer to standard x'test statistics for independence,where Yates refers to Yates 2 x 2 continuity correction.The cross-product ratio is the ratio of the product of principal diagonal cell counts to the product of the off-diagonal counts. entire period 1976-1987.The results are similar to those reported in Table 3.The significance of apparent persistence has fallen.However, both the cross-section and the self-financing portfolio results indicate that there is still statistically significant evidence that performance persists for at least part of the period. The persistence of negative performance is not surprising.Negative performance can persist where a subset of managers are immune from periodic performance review and where it is difficult to short sell shares of mutual funds.3 It can be only institutional reasons such as In fact,Hendricks,Patel,and Zeckhauser provide little reliable evidence of"hot hands."Using either the value-weighted or the equal-weighted CRSP index benchmark,there is no significant 558

Survivorsbip Bias in Performance Studies Table 4 Regression-based measures of persistence in performance,1976-1987(excluding poor performers) Cross-section regression approach' Period January 1976-December 1981: 2=.1463+.2736à1 (5.48)(3.13) R2=.113;n=79 Period January 1979-December 1984: a■.0317-.18158 (1.04)(-1.55) 2=.029:n=82 Period January 1982-December 1987: 3=-.0334+.0521a (-3.09)(.81) R2=.008:n=88 Time-series self-financing portfolio approach? Period January 1977-December 1987: rw=.0008.-,0015rm (2.15)(-.20) 2=.000:n=132 (t-values in parentheses) This table is intended to show the effect that different standards of performance review might have on measures of persistence in returns.The procedures and data are the same as those presented in Table 2,with the exception that managers are excluded whose average value of Jensen's a is negative over the entire period for which data is available. "Jensen's a is computed for the sample of funds described in Table 1 for each of four three-year subperiods,of data starting in 1976-1978,excluding those funds that performed poorly over the entire period.Each panel reports results from the cross-section regression of performance measures on prior performance measures. This corresponds to the measure employed by Hendricks,Patel,and Zeckhauser (1991)with four quarter evaluation and holding periods,excluding poor performing funds. these that allow a fund with sustained poor performance to survive.6 It is the persistence of positive returns that would be remarkable,if true.The problems of interpretation caused by the ex post definition of winners and losers suggests that the results may also be sensitive to the most obvious source of ex post conditioning:survival. It is clear that all managers depicted in the 2 x 2 tables have passed the market test,at least for the successive three-year periods.We have no data for the managers who did not survive.If the probability of persistence of positive performance.The only benchmark for which they find any statistically significant evidence of persistence in positive performance is a self-created benchmark consisting of an equal-weighted average of returns on the mutual funds in their sample. Hendricks,Patel,and Zeckhauser(1991)give the example of the 44 Wall Street funds that survived the period 1975-1988 with a negative annual a of -1.90 (relative to the value-weighted CRSP index)and -4.27 (relative to the equal-weighted CRSP index).One potential explanation for the persistence of negative performance might be that mutual fund data compute returns after fees but before sales and load charges.The negative performance may simply reflect the persistence of high fees. 5591

Tbe Review of Financial Studtes/v 5 n 4 1992 survival depends on past performance to date,we might expect that the set of managers who survive will have a higher ex post return than those who did not survive.Managers who take on significant risk and lose may also have a low probability of survival.This observation suggests that past performance numbers are biased by survivorship; we only see the track record of those managers who have survived. This does not suggest,however,that performance persists.If anything, it suggests the reverse.If survival depends on cumulative perfor- mance,a manager who does well in one period does not have to do so well in the next period in order to survive.Certainly,this survi- vorship argument cannot explain results suggested by Table 1.More. over,there is a general perception that the survivorship bias effect cannot be very substantial.In a recent study,Grinblatt and Titman (1989)report that the survivorship effect accounts for only about 0.1 to 0.4 percent return per year measured on a risk-adjusted basis before transaction costs and fees.We shall see that the survivorship bias in mean excess returns is small in magnitude relative to a more subtle, yet surprisingly powerful,survival bias that implies persistence in performance. A manager who takes on a great deal of risk will have a high prob- ability of failure.However,if he or she survives,the probability is that this manager took a large bet and won.High returns persist.If they do not persist,we would not see this high-risk manager in our sample.7 Note that this is a total risk effect;risk-adjustment using B or other measure of nonidiosyncratic risk may not fully correct for it. To illustrate this effect,observe in Table 3 that the additional 10 firms that come into the database in 1979-1981 are all ex post successful. The average value of residual risk (0.0323)for the new entrants is significantly greater than that of the population of managers(0.0242), with a t-value of 2.02.The new entrants who survived took on more risk and were successful. The magnitude of the persistence will depend on the precise way in which survivorship depends on past performance and whether there is any strategic risk management response on the part of sur- viving money managers.8 The intent is to show that the apparent Hendricks,Patel,and Zeckhauser (1991)argue that because fund data is eliminated from their database as the fund ceases to exist or is merged into other funds,their sample is free of survivorship bias effects.However,all funds considered at each evaluation point survived at least until the end of an evaluation period that could extend from one quarter to two years.They are excluded from the analysis subsequent to the evaluation period.The numerical example given in Section 2 of this article matches this experimental design,and provides a counterexample to a presumption of freedom from survivorship bias effects.The results of such a study would be free of survival bias only if it can be established that the probability of termination or elimination from the sample is unrelated to performance.However,Hendricks,Patel,and Zeckhauser indicate (note 5)that,in fact,funds that go under do quite poorly in the quarter of demise. .We show in the Appendix that the effect is mitigated somewhat where cumulative performance 560

Survivorsbip Bias in Performance Studies persistence of performance documented in Tables 1 and 2 is not necessarily any indication of skill among surviving managers. To the extent that survivorship depends on past returns,ranking managers who survive by realized returns may induce an apparent persistence in performance.Survivorship implies that managers will be selected according to total risk.One way of explaining the Table 1 results is to observe that the set of managers studied represent a heterogeneous mix of management styles.Each management style is characterized by a certain vector of risk attributes.By examining the survivors,we are really only looking at those styles that were ex post successful.It may appear that one resolution of this problem is to concentrate on only one defined management style.There are two problems with this approach.In the first instance,we have to be careful to define the style sufficiently broadly that there are more than a few managers represented.In the second instance,we may exac- erbate the effect if our definition of manager style is synonymous with taking high total risk positions. We only observe the performance of managers who survive per. formance evaluations.The purpose of this article is to examine the extent to which this fact is sufficient to explain the magnitude of persistence we seem to see in the data.In Section 1,we examine the relationship between total risk differentials and survivorship-induced persistence in performance.In Section 2,we present some numerical results that show that a very small survivorship effect is sufficient to generate a strong and significant appearance of dependence in serial returns.We conclude in Section 3. 1.Relationship between Volatility and Returns Induced by Survivorship There are many possible quite complex sample selection rules.We will look at the implications of one class of these rules.Our purpose in this section is to demonstrate that sample survivorship bias is a force that can lead to persistence in performance rankings.For sim- plicity,assume all distributions are atomless.Our tool is the following lemma. rather than one-period performance is used as a survival criterion.The analysis of a strategic response is beyond the scope of this article.A possible strategic response is for surviving managers who are subject to the same survival criterion to converge in residual risk characteristics.The results in the next section require only that the ranking of managers by residual risk be constant.This kind of strategic response would also tend to mitigate the effect.This analysis is complicated by the fact that survival criteria are not necessarily the same for all managers. 5611