
On the Impossibility of Informationally Efficient Markets By SANFORD J.GROSSMAN AND JOSEPH E.STIGLITZ* If competitive equilibrium is defined as a Jectures concerning certain properties of the situation in which prices are such that all equilibrium.The remaining analytic sections arbitrage profits are eliminated,is it possible of the paper are devoted to analyzing in that a competitive economy always be in detail an important example of our general equilibrium?Clearly not,for then those who model,in which our conjectures concerning arbitrage make no (private)return from the nature of the equilibrium can be shown their (privately)costly activity.Hence the to be correct.We conclude with a discussion assumptions that all markets,including that of the implications of our approach and for information,are always in equilibrium results,with particular emphasis on the rela- and always perfectly arbitraged are incon- tionship of our results to the literature on sistent when arbitrage is costly. “efficient capital markets.” We propose here a model in which there is an equilibrium degree of disequilibrium: I.The Model prices reflect the information of informed individuals(arbitrageurs)but only partially, Our model can be viewed as an extension so that those who expend resources to ob- of the noisy rational expectations model in- tain information do receive compensation. troduced by Robert Lucas and applied to How informative the price system is de- the study of information flows between pends on the number of individuals who are traders by Jerry Green (1973);Grossman informed;but the number of individuals (1975,1976,1978);and Richard Kihlstrom who are informed is itself an endogenous and Leonard Mirman.There are two assets: variable in the model. a safe asset yielding a return R,and a risky The model is the simplest one in which asset,the return to which,u,varies ran- prices perform a well-articulated role in con- domly from period to period.The variable u veying information from the informed to the consists of two parts, uninformed.When informed individuals ob- serve information that the return to a secur- (1) u=0+e ity is going to be high,they bid its price up, and conversely when they observe informa- where 6 is observable at a cost c,and e is tion that the return is going to be low.Thus unobservable.Both 0 and e are random the price system makes publicly available variables.There are two types of individu- the information obtained by informed indi- als,those who observe 0(informed traders), viduals to the uniformed.In general,how- and those who observe only price (unin- ever,it does this imperfectly;this is perhaps formed traders).In our simple model,all lucky,for were it to do it perfectly,an individuals are,ex ante,identical;whether equilibrium would not exist. they are informed or uninformed just de- In the introduction,we shall discuss the pends on whether they have spent c to ob- general methodology and present some con- tain information.Informed traders'de- mands will depend on and the price of the .University of Pennsylvania and Princeton Univer- risky asset P.Uninformed traders'demands sity,respectively.Research support under National Sci- ence Foundation grants SOC76-18771 and SOC77- An alternative interpretation is that 0 is a "mea- 15980 is gratefully acknowledged.This is a revised surement"of u with error.The mathematics of this version of a paper presented at the Econometric alternative interpretation differ slightly,but the results Society meetings,Winter 1975,at Dallas,Texas. are identical. 393

394 THE AMERICAN ECONOMIC REVIEW JUNE 1980 will depend only on P,but we shall assume which the informed can gain relative to the that they have rational expectations;they uninformed-is reduced. learn the relationship between the distribu- (b)Even if the above effect did not tion of return and the price,and use this in occur,the increase in the ratio of informed deriving their demand for the risky assets.If to uninformed means that the relative gains x denotes the supply of the risky asset,an of the informed,on a per capita basis,in equilibrium when a given percentage,入,of trading with the uninformed will be smaller. traders are informed,is thus a price function We summarize the above characterization P.(,x)such that,when demands are for- of the equilibrium of the economy in the mulated in the way described,demand following two conjectures: equals supply.We assume that uninformed Conjecture 1:The more individuals who traders do not observe x.Uninformed are informed,the more informative is the traders are prevented from learning via price system. observations of P(,x)because they can- Conjecture 2:The more individuals who not distinguish variations in price due to are informed,the lower the ratio of expected changes in the informed trader's informa- utility of the informed to the uninformed. tion from variations in price due to changes (Conjecture I obviously requires a defini- in aggregate supply.Clearly,P(,x)reveals tion of "more informative";this is given in some of the informed trader's information the next section and in fn.7.) to the uninformed traders. The equilibrium number of informed and We can calculate the expected utility of uninformed individuals in the economy will the informed and the expected utility of the depend on a number of critical parameters: uninformed.If the former is greater than the the cost of information,how informative the latter (taking account of the cost of infor- price system is (how much noise there is to mation),some individuals switch from being interfere with the information conveyed by uninformed to being informed (and con- the price system),and how informative the versely).An overall equilibrium requires the information obtained by an informed indi- two to have the same expected utility.As vidual is. more individuals become informed,the ex- Conjecture 3:The higher the cost of pected utility of the informed falls relative information,the smaller will be the equi- to the uninformed for two reasons: librium percentage of individuals who are (a)The price system becomes more in- informed. formative because variations in a have a Conjecture 4:If the quality of the in- greater effect on aggregate demand and thus formed trader's information increases,the on price when more traders observe 0.Thus, more their demands will vary with their more of the information of the informed is information and thus the more prices will available to the uninformed.Moreover,the vary with 0.Hence,the price system be- informed gain more from trade with the comes more informative.The equilibrium uninformed than do the uninformed.The proportion of informed to uninformed may informed,on average,buy securities when be either increased or decreased,because they are "underpriced"and sell them when even though the value of being informed has they are“overpriced'”(relative to what increased due to the increased quality of 0, they would have been if information were the value of being uninformed has also in- equalized).As the price system becomes creased because the price system becomes more informative,the difference in their in- more informative. formation-and hence the magnitude by Conjecture 5:The greater the magni- tude of noise,the less informative will the price system be,and hence the lower the 2The framework described herein does not explicitly model the effect of variations in supply,i.e.,x on expected utility of uninformed individuals. commodity storage.The effect of futures markets and Hence,in equilibrium the greater the magni- storage capabilities on the informativeness of the price tude of noise,the larger the proportion of system was studied by Grossman (1975,1977). informed individuals

VOL.70 NO.3 GROSSMAN AND STIGLITZ:EFFICIENT MARKETS 395 Conjecture 6:In the limit,when there is the conjectures provided above can be veri- no noise,prices convey all information,and fied.The next sections are devoted to solv- there is no incentive to purchase informa- ing for the equilibrium in this particular tion.Hence,the only possible equilibrium is example.> one with no information.But if everyone is uninformed,it clearly pays some individual II.Constant Absolute Risk-Aversion Model to become informed.3 Thus,there does not exist a competitive equilibrium. A.The Securities Trade among individuals occurs either be- cause tastes (risk aversions)differ,endow- The ith trader is assumed to be endowed ments differ,or beliefs differ.This paper with stocks of two types of securities:Mi focuses on the last of these three.An inter- the riskless asset,and Xi,a risky asset.Let P esting feature of the equilibrium is that be- be the current price of risky assets and set liefs may be precisely identical in either one the price of risk free assets equal to unity. of two situations:when all individuals are The ith trader's budget constraint is informed or when all individuals are unin- formed.This gives rise to: (2) PX,+M,=Wo≡M,+PX Conjecture 7:That,other things being equal,markets will be thinner under those Each unit of the risk free asset pays R conditions in which the percentage of indi- “dollars'”at the end of the period,while viduals who are informed (A)is either near each unit of the risky asset pays u dollars.If zero or near unity.For example,markets at the end of the period,the ith trader holds will be thin when there is very little noise in a portfolio (M,X )his wealth will be the system(so A is near zero),or when costs of information are very low (so A is near (3) W=RM +ux unity). In the last few paragraphs,we have pro- B.Individual's Utility Maximization vided a number of conjectures describing the nature of the equilibrium when prices Each individual has a utility function convey information.Unfortunately,we have V(W).For simplicity,we assume all indi- not been able to obtain a general proof of viduals have the same utility function and any of these propositions.What we have so drop the subscripts i.Moreover,we been able to do is to analyze in detail an assume the utility function is exponential, interesting example,entailing constant ab- i.e., solute risk-aversion utility functions and normally distributed random variables.In V(Wu)=-e-ow, a>0 this example,the equilibrium price distribu- where a is the coefficient of absolute risk tion can actually be calculated,and all of aversion.Each trader desires to maximize expected utility,using whatever information is available to him,and to decide on what 3That is,with no one informed,an individual can information to acquire on the basis of the only get information by paying c dollars,since no consequences to his expected utility. information is revealed by the price system.By paying Assume that in equation (1)0 and e have c dollars an individual will be able to predict better than the market when it is optimal to hold the risky a multivariate normal distribution,with asset as opposed to the risk-free asset.Thus his ex- (4) Ee=0 pected utility will be higher than an uninformed person gross of information costs.Thus for c sufficiently low (5) E0e=0 all uninformed people will desire to be informed. 4See Grossman (1975,1977)for a formal example of (6) Var(u*0)=Vare*=02>0 this phenomenon in futures markets.See Stiglitz(1971, 1974)for a general discussion of information and the SThe informational equilibria discussed here may possibility of nonexistence of equilibrium in capital not,in general,exist.See Green (1977).Of course,for markets. the utility function we choose equilibrium does exist

396 THE AMERICAN ECONOMIC REVIEW JUNE 1980 since 0 and e are uncorrelated.Throughout Then,we can write for the uninformed this paper we will put a above a symbol to individual emphasize that it is a random variable. Since Wi:is a linear function of e,for a given portfolio allocation,and a linear func- (7)E(v(Wi)IP)=-exp-aE[WilP-] tion of a normally distributed random vari- able is normally distributed,it follows that -2 var[WilP"]) Wi;is normal conditional on 0.Then,using (2)and (3)the expected utility of the in- formed trader with information 0 can be --exp-a(RWo+Xu(E[u*lP*]-RP) written (7) E(V(W)川8)= -号xar[u*p*]}] -exp(-afE[Wil]-var[wi])) The demands of the uninformed will thus be a function of the price function P*and the actual price P. --cxp(-aRWo+X,(E(u*l0)-RP) (8)Xu(P;P*) =E[*P*(0,x)=P]-RP -x好varu*o)]) a var[u*P*(0.x)=P] C.Equilibrium Price Distribution --exp(-aRWo+x(0-RP) If A is some particular fraction of traders who decide to become informed,then define -x]) an equilibrium price system as a function of (0,x),P(0,x),such that for all (0,x)per capita demands for the risky assets equal where X,is an informed individual's de- supplies: mand for the risky security.Maximizing (7) with respect to X,yields a demand function (9) 入X(P(8,x),9) for risky assets: X,(P.0)=0-RP +(I-入)X(P(9x):P*)=x (8) a03 The function P(6,x)is a statistical The right-hand side of(8)shows the familiar equilibrium in the following sense.If over result that with constant absolute risk aver- time uninformed traders observe many re- sion,a trader's demand does not depend on alizations of (u,P),then they learn the wealth;hence the subscript i is not on the joint distribution of (u*,P*).After all learn- left-hand side of(8). ing about the joint distribution of (u*,P*) We now derive the demand function for ceases,all traders will make allocations and the uninformed.Let us assume the only form expectations such that this joint dis- source of "noise"is the per capita supply of tribution persists over time.This follows the risky security x. from (8),(8),and (9),where the market- Let P*()be some particular price func- clearing price that comes about is the one tion of (,x)such that u*and P*are jointly which takes into account the fact that unin- normally distributed.(We will prove that formed traders have learned that it contains this exists below.) information

VOL.70N0.3 GROSSMAN AND STIGLITZ:EFFICIENT MARKETS 397 We shall now prove that there exists an For each replication of the economy,0 is equilibrium price distribution such that p* the information that uninformed traders and u*are jointly normal.Moreover,we would like to know.But the noise x* shall be able to characterize the price dis- prevents w*from revealing 0.How well- tribution.We define informed uninformed traders can become from observing P*(equivalently w*)is (10a) @-0-笑x- measured by Var[w*0].When Varlw]is zero,w*and are perfectly correlated. Hence when uninformed firms observe w, forλ>0,and define wo(9,x)as the number: this is equivalent to observing 6.On the other hand,when Var[w]is very large, (10b)wo(0.x)=x for all (0,x) there are "many"realizations of w*that are associated with a given 0.In this case the where w,is just the random variable 0,plus observation of a particular w*tells very noise.6 The magnitude of the noise is in- little about the actual which generated it.7 versely proportional to the proportion of From equation (11)it is clear that large informed traders,but is proportional to the noise (high Varx*)leads to an imprecise variance of e.We shall prove that the price system.The other factor which de- equilibrium price is just a linear function of termines the precision of the price system wa.Thus,if A>0,the price system conveys (a'a/A2)is more subtle.When a is small information about 0,but it does so imper- (the individual is not very risk averse)or o fectly. is small (the information is very precise),an informed trader will have a demand for D.Existence of Equilibrium and risky assets which is very responsive to a Characterization Theorem changes in 0.Further,the larger A is,the more responsive is the total demand of in- THEOREM 1:If (0*,e*,x*)has a nonde- formed traders.Thus small (aoA2)means generate joint normal distribution such that that the aggregate demand of informed 0*,e*,and x*are mutually independent,then traders is very responsive to 6.For a fixed there exists a solution to (9)which has the amount of noise (i.e.,fixed Varx*)the form P(0,x)=a+a2wa(0,x),where a and larger are the movements in aggregate de- a are real numbers which may depend on入, mand which are due to movements in 0,the such that a2>0.(If入=0,the price contains more will price movements be due to move- no information about 0.)The exact form of ments in 0.That is,x*becomes less im- P,(0,x)is given in equation (A10)in Appen- portant relative to 0 in determining price dix B.The proof of this theorem is also in movements.Therefore,for small (ao3/A2) Appendix B. uninformed traders are able to confidently know that price is,for example,unusually The importance of Theorem 1 rests in the high due to 6 being high.In this way infor- simple characterization of the information mation from informed traders is transferred in the equilibrium price system:P*is infor- to uninformed traders. mationally equivalent to w*.From (10)w* isa“mean-preserving spread”off;i.e, E[w]=0 and (11) Var[wxle]= doi Varx λ2 7Formally,w is an experiment in the sense of Blackwell which gives information about 0.It is easy to show that,ceteris paribus,the smaller Var(w)the more "informative"(or sufficient)in the sense of 6If y'=y+Z,and E[Zly]=0,then y'is just y plus Blackwell,is the experiment;see Grossman,Kihlstrom, noise. and Mirman (p.539)

398 THE AMERICAN ECONOMIC REVIEW JUNE 1980 E.Equilibrium in the Information Market F.Existence of Overall Equilibrium What we have characterized so far is the Theorem 2 is useful,both in proving the equilibrium price distribution for given A. uniqueness of overall equilibrium and in We now define an overall equilibrium to be analyzing comparative statics.Overall equi- a pair (A,P*)such that the expected utility librium,it will be recalled,requires that for of the informed is equal to that of the unin- O1, ness of Woi,u,6,and x. then (0,P)is an overall equilibrium.For all In evaluating the expected utility ofW, price equilibria P,which are monotone func- we do not assume that a trader knows which tions of wx,there exists a unique overall realization of he gets to observe if he equilibrium(入,P). pays c dollars.A trader pays c dollars and then gets to observe some realization of * PROOF: The overall expected utility of W averages The first three sentences follow im- over all possible 0*,e*,x*,and Woi.The mediately from the definition of overall variable Wo:is random for two reasons. equilibrium given above equation (12),and First from(2)it depends on P(,x),which Theorems I and 2.Uniqueness follows from is random as (,x)is random.Secondly,in the monotonicity of y()which follows from what follows we will assume that X,is ran- (All)and (14).The last two sentences in dom. the statement of the theorem follow im- We will show below that EV(W)/ mediately. Ev(W)is independent of i,but is a func- tion of入,a,c,anda.More precisely,.in In the process of proving Theorem 3,we Appendix B we prove have noted THEOREM 2:Under the assumptions of COROLLARY 1:Y(A)is a strictly mono- Theorem 1,and if X:is independent of tone increasing function of A. (u*,0*,x*)then This looks paradoxical;we expect the (13 EV(WA) Var(u*0) ratio of informed to uninformed expected utility to be a decreasing function of A.But, EV(W) Var(u*wa) we have defined utility as negative.Therefore
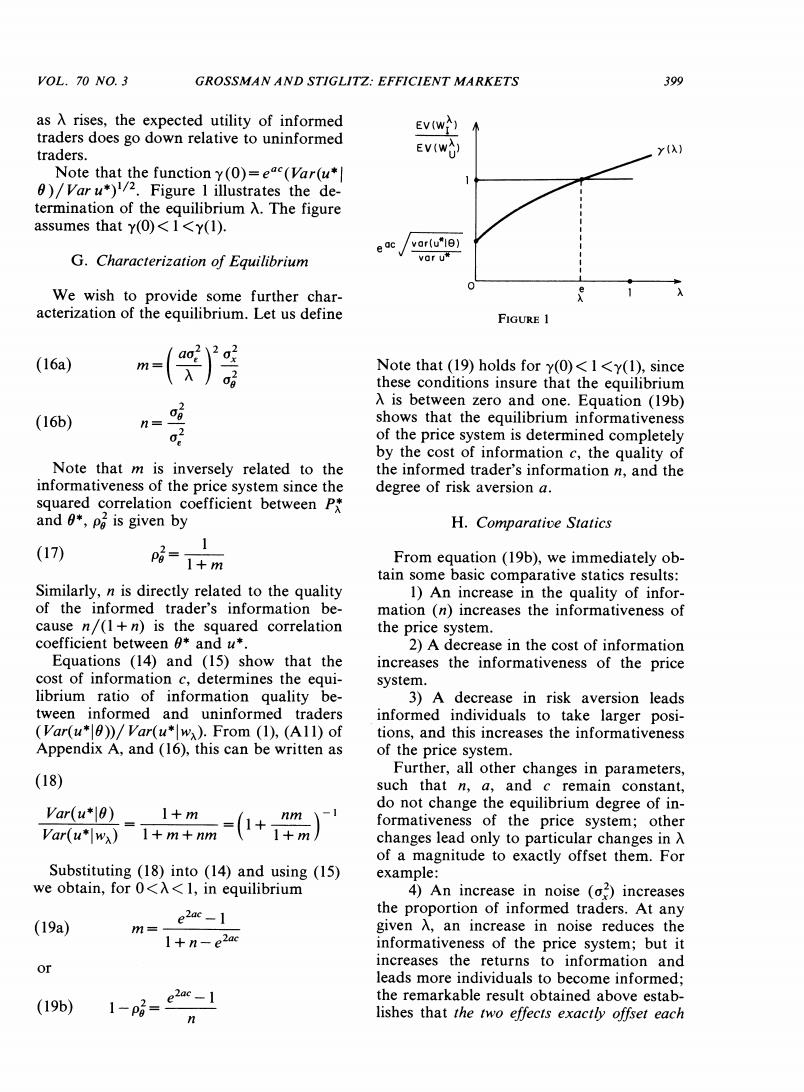
VoL.70N0.3 GROSSMAN AND STIGLITZ:EFFICIENT MARKETS 399 as A rises,the expected utility of informed EV(W) traders does go down relative to uninformed traders. EV(W) Note that the function y(0)=eac(Var(u* 0)/Var u*)1/2.Figure 1 illustrates the de- termination of the equilibrium A.The figure assumes that y(0)<1<y(1). e ac var(u"1e) G.Characterization of Equilibrium vor u We wish to provide some further char- acterization of the equilibrium.Let us define FIGURE 1 (16a) Note that (19)holds for y(0)<I<y(1),since these conditions insure that the equilibrium A is between zero and one.Equation (19b) (16b) n= shows that the equilibrium informativeness of the price system is determined completely by the cost of information c,the quality of Note that m is inversely related to the the informed trader's information n,and the informativeness of the price system since the degree of risk aversion a. squared correlation coefficient between P* and 0*,pa is given by H.Comparative Statics 1 (17) p6=1+m From equation(19b),we immediately ob- tain some basic comparative statics results: Similarly,n is directly related to the quality 1)An increase in the quality of infor- of the informed trader's information be- mation (n)increases the informativeness of cause n/(1+n)is the squared correlation the price system. coefficient between and u*. 2)A decrease in the cost of information Equations (14)and (15)show that the increases the informativeness of the price cost of information c,determines the equi- system. librium ratio of information quality be- 3)A decrease in risk aversion leads tween informed and uninformed traders informed individuals to take larger posi- (Var(u*))/Var(u*wa).From (1),(A11)of tions,and this increases the informativeness Appendix A,and (16),this can be written as of the price system. Further,all other changes in parameters, (18) such that n,a,and c remain constant, do not change the equilibrium degree of in- formativeness of the price system;other Var(u*wx)1+m+nm changes lead only to particular changes in A of a magnitude to exactly offset them.For Substituting(18)into (14)and using (15) example: we obtain,for 0<A<1,in equilibrium 4)An increase in noise (o)increases e2ac-I the proportion of informed traders.At any (19a) m=- given入,an increase in noise reduces the +n-e2ac informativeness of the price system;but it or increases the returns to information and leads more individuals to become informed; the remarkable result obtained above estab- (19b) lishes that the two effects exactly offset each

400 THE AMERICAN ECONOMIC REVIEW JUNE 1980 other so that the equilibrium informative- improvement in the precision of informed ness of the price system is unchanged.This traders'information,with the cost of the can be illustrated diagrammatically if we information fixed,increases the benefit of note from(l6a)that for a given入,anin- being informed.However,some of the im- crease in o raises m which from(18)lowers proved information is transmitted,via a (Var(u*0))/Var(u*wa).Thus from (14)a more informative price system,to the unin- rise in o:leads to a vertical downward shift formed;this increases the benefits of being of the y(A)curve in Figure 1,and thus a uninformed.If n is small,both the price higher value ofλe. system m is not very informative and the 5)Similarly an increase in o2 for marginal value of information to informed a constant n (equivalent to an increase in traders is high.Thus the relative benefits of the variance of u since n is constant)leads being informed rises when n rises;implying to an increased proportion of individuals that the equilibrium A rises.Conversely becoming informed-and indeed again just when n is large the price system is very enough to offset the increased variance,so informative and the marginal value of infor- that the degree of informativeness of the mation is low to informed traders so the price system remains unchanged.This can relative benefits of being uninformed rises. also be seen from Figure I if (16)is used to 7)From (14)it is clear that an increase note that an increase in o2 with n held in the cost of information c shifts the y(A) constant by raising og leads to an increase in curve up and thus decreases the percentage m for a given A.From (18)and (14)this of informed traders. leads to a vertical downward shift of the The above results are summarized in the Y(A)curve and thus a higher value of A. following theorem. 6)It is more difficult to determine what happens if,say og increases,keeping o con- THEOREM 4:For equilibrium A such that stant (implying a fall in o2),that is,the 00 and price is negative so that A falls due to an increase in the fully informative. precision of the informed trader's information.Simi- larly if n is sufficiently small,the derivative is positive 1)As the cost of information goes to and thus入rises. zero,the price system becomes more infor-

V0L.70N0.3 GROSSMAN AND STIGLITZ:EFFICIENT MARKETS 401 mative,but at a positive value of c,say c,all while ifλ>0,by(l8) traders are informed.From (14)and (15)6 satisfies EV(WA) Var(u*0) EV(W) 1+n =I m+1 Var(u*w) But if o2=0 or o2=0,then m=0,nm=0 for λ>0,and hence 2)From (19a)as the precision of the informed trader's information n goes to in- EV(WA) finity,i.e,a→0 and o→o,o2 held fixed, (21) lim =eac the price system becomes perfectly informa- EV(W) tive.Moreover the percentage of informed traders goes to zero!This can be seen from It immediately follows that (l8)and(15).That is,asoe→0,nm/(1+m) must stay constant for equilibrium to be THEOREM 5:(a)If there is no noise (2= maintained.But from (19b)and (17),m 0),an overall equilibrium does not exist if falls as o2 goes to zero.Therefore nm must (and only if)eae0 is (19a)implies that m does not change as o2 not an equilibrium since by (21)Y(A)>1. changes,the informativeness of the price (b)If o2=0 and og=o so that informa- system is unchanged as o20. tion is perfect,.then forλ>0,nm=0by(l6) Assume that c is small enough so that it is and hence y(A)>I by (21).From(20)Y(0)= worthwhile for a trader to become informed 00 is not an is less than unity so that A=0 cannot be an equilibrium.On the other hand,if no equilibrium;but when A>0,it is greater traders are informed,then each uninformed than unity.That is,if o2=0 or o2=0,the trader learns nothing from the price system, ratio of expected utilities is not a continuous and thus he has a desire to become in- function of入at入=0. formed (if eac<(1+n)2).Similarly if the This follows immediately from observing informed traders get perfect information, that at入=0,Var(u|wo)=Varu*,and thus then their demands are very sensitive to by(14) their information,so that the market-clear- (20) EV(W) ing price becomes very sensitive to their information and thus reveals a to the unin- EV(WO) 02+0 formed.Hence all traders desire to be un- informed.But if all traders are uninformed, each trader can eliminate the risk of his portfolio by the purchase of information,so +n each trader desires to be informed

402 THE AMERICAN ECONOMIC REVIEW JUNE 1980 In the next section we show that the non- ples'beliefs differ slightly,then the competi- existence of competitive equilibrium can be tive equilibrium allocation that an individ- thought of as the breakdown of competitive ual gets will be only slightly different from markets due to lack of trade.That is,we will his initial endowment.Hence,there will show that as o gets very small,trade goes only be a slight benefit to entering the com- to zero and markets serve no function.Thus petitive market.This could,for sufficiently competitive markets close for lack of trade high operating costs,be outweighed by the “before”equilibrium ceases to exist at cost of entering the market. 02=0. The amount of trade occurring at any date is a random variable;a function of 0 III.On the Thinness of Speculative Markets and x.It is easy to show that it is a normally distributed random variable.Since one of In general,trade takes place because the primary determinants of the size of traders differ in endowments,preferences, markets is differences in beliefs,one might or beliefs.Grossman (1975,1977,1978)has have conjectured that markets will be thin, argued that differences in preferences are in some sense,if almost all traders are either not a major factor in explaining the magni- informed or uninformed.This is not,how- tude of trade in speculative markets.For ever,obvious,since the amount of trade by this reason the model in Section II gave all any single trader may be a function of A as traders the same risk preferences (note that well,and a few active traders can do the job none of the results in Section II are affected of many small traders.In our model,there is by letting traders have different coefficients a sense,however,in which our conjecture is of absolute risk aversion).In this section we correct. assume that trade requires differences in We first calculate the magnitude of trades endowments or beliefs and dispense with as a function of the exogenous parameters,0 differences in risk preference as an explana- and x.Let h=o2,=Ex*,and 0=E0* tory variable. (The actual trades will depend on the dis- There is clearly some fixed cost in operat- tribution of random endowments across all ing a competitive market.If traders have to of the traders,but these we shall net out.) bear this cost,then trade in the market must Per capita net trade is 10 be beneficial.Suppose traders have the same endowments and beliefs.Competitive equi- (22) librium will leave them with allocations 名-x=-(m+)x- which are identical with their initial endow- ments.Hence,if it is costly to enter such a +[(m+1)n-1](0-0)+xm competitive market,no trader would ever enter.We will show below that in an im- +[1+m+m] portant class of situations,there is continu- ity in the amount of net trade.That is,when 10Calculation of distribution of net trades initial endowments are the same and peo- 入 (0-RP) 9In the model described in Section II it was assumed (-[(-RR1+m)n+0--(x-x that an individual's endowment X:is independent of the market's per capita endowment x*.This was done ah(1+m+nm)n primarily so there would not be useful information in an individual's endowment about the total market en- 9-RB+-+m dowment.Such information would be useful in equi- ah 1+m+m librium because an individual observes P(,x).If due to observing Xi,he knows something about x,then by observing P(,x),X.is valuable in making inferences about 0.To take this into account is possible,but would add undue complication to a model already (-m+)n-0-)+(x-) overburdened with computations. ah(1+m+Anm)n