
A Theory of Fads,Fashion,Custom,and Cultural Change as Informational Cascades Sushil Bikhchandani,David Hirshleifer, and Ivo Welch University of California,Los Angeles An informational cascade occurs when it is optimal for an individual, having observed the actions of those ahead of him,to follow the behavior of the preceding individual without regard to his own in- formation.We argue that localized conformity of behavior and the fragility of mass behaviors can be explained by informational cas- cades. Let them alone:they be blind leaders of the blind.And if the blind lead the blind,both shall fall into the ditch. [Matthew 15:14] I.Introduction One of the most striking regularities of human society is localized conformity.Americans act American,Germans act German,and Indi- We thank Daniel Asquith,Christopher Barry,Gary S.Becker,Michael J.Brennan, Colin Camerer,Darrell Duffie,Robert Ellickson,Dan Friedman,Stephen J.Gould, Jack Hirshleifer,David Hull,Timur Kuran,Steve Lippman,John Mamer,Hubert Markl,Robert May,David Nachman,Jonathan Paul,Tom Philipson,Ivan P.L.Png, Thomas Schelling,Max Steuer,Sheridan Titman,Gordon Tullock,the editor,two anonymous referees,the members of the Rational Choice seminar at the University of Chicago,and seminar participants at University of California,Berkeley,Hebrew University,Jerusalem,the National Bureau of Economic Research,National Taiwan University,Northwestern University,the University of Pittsburgh,and the University of Utah for helpful comments and discussions.Parts of this paper subsume parts of an earlier paper,"Sequential Sales,Path Dependence,and Cascades"(September 1989 version)by Welch. [Journal of Polirical Ecomomy,1992.vol.100.no.5] 1992 by The University of Chicago.All rights reserved.0022-3808/92/0005-0001$01.50 992

INFORMATIONAL CASCADES 993 ans act Indian.At one school teenagers take drugs,but at another they"just say no."English and American youths enthusiastically en- listed to fight in World War I,but pacifist sentiments prevailed prior to World War II and in the 1960s. Four primary mechanisms have been suggested for uniform social behavior:(1)sanctions on deviants,?(2)positive payoff externalities,3 (3)conformity preference,4 and(4)communication.5 The first three theories can explain why society may fix on undesirable choices,or at least why the social outcome may be history-dependent.Sanctions can enforce a malevolent dictatorship,payoff externalities can drive a better technology to extinction (e.g.,the beta video system),and people with a direct preference for conforming may jump on the bandwagon for fairly arbitrary behavior (e.g.,bell-bottom jeans). These effects tend to bring about a rigid conformity that cannot be broken by small shocks.Indeed,the longer the bandwagon continues, the more robust it becomes.The fourth theory implies convergence toward the correct outcome if communication is credible and costless. It does not explain why mass behavior is error-prone. None of these theories explains why mass behavior is often fragile in the sense that small shocks can frequently lead to large shifts in behavior.6 For example,cohabitation of unmarried couples was viewed as scandalous in the 1950s,was flaunted in the 1960s,and was hardly noticed in the 1980s.Colleges in which students demonstrated and protested in the 1960s became quiet in the 1980s.The recent rejection of communism began in Poland and later spread rapidly among other Eastern European countries.Religious movements,re- vivals,and reformations,started by a few zealots,sometimes sweep across populations with astonishing rapidity.Addiction to and social attitudes associated with alcohol,cigarettes,and illegal drugs have fluctuated widely. This paper offers an explanation not only of why people conform but also of why convergence of behavior can be idiosyncratic and I Boyd and Richerson(1985)examine several general models of cultural transmis- sion that could be consistent with these mechanisms.Becker(1991)analyzes conformity in product demand in a model that is also consistent with several of these mechanisms See,e.g..Akerlof (1980).Bendor and Mookherjee (1987),Coleman (1987). Hirshleifer and Rasmusen (1989),and Kuran(1989). 3See,e.g..Schelling (1960,1978).Dybvig and Spatt(1983).Farrell and Saloner (1986),Katz and Shapiro (1986),and Arthur (1989).For example,conventions such as driving on the right-(or left-)hand side of the road are self-enforcing,once a few individuals follow the convention. 4 In Jones(1984),individuals inherently wish to conform with the behavior of others. 5 Conformity can be achieved if early individuals explain the benefits of alternatives to later ones (see,e.g.,Rogers 1983). 6 In Kuran(1989),sanction-enforced behavior for specific sets of exogenous parame- ter values can be sensitive to small shifts

994 JOURNAL OF POLITICAL ECONOMY fragile.In our model,individuals rapidly converge on one action on the basis of some but very little information.If even a little new information arrives,suggesting that a different course of action is optimal,or if people even suspect that underlying circumstances have changed(whether or not they really have),the social equilibrium may radically shift.Our model,which is based on what we call "informa- tional cascades,"explains not only conformity but also rapid and short-lived fluctuations such as fads,fashions,booms,and crashes.In the theories of conformity discussed earlier,small shocks lead to big shifts in mass behavior only if people happen to be very close to the borderline between alternatives.Informational cascades explain why society,on the basis of little information,will systematically tend to land close to the borderline,causing fragility. An informational cascade occurs when it is optimal for an individ- ual,having observed the actions of those ahead of him,to follow the behavior of the preceding individual without regard to his own information.Consider the submission of this paper to a journal.The referee will read the paper,assess its quality,and accept or reject it. Suppose that a referee at a second journal learns that the paper was previously rejected.Under the assumption that the referee cannot assess the paper's quality perfectly,knowledge of the prior rejection should tilt him toward rejection.Suppose now that the second journal also rejects and that when the paper is submitted to a third journal, the third referee learns that the paper was rejected at two previous journals.Clearly,this further raises the chance of rejection. In a fairly general setting with sequential choices,we show that at some stage a decision maker will ignore his private information and act only on the information obtained from previous decisions.Once this stage is reached,his decision is uninformative to others.There- fore,the next individual draws the same inference from the history of past decisions;thus if his signal is drawn independently from the same distribution as previous individuals',this individual also ignores his own information and takes the same action as the previous indi- vidual.In the absence of external disturbances,so do all later indi- viduals. The paper submission example is special in that only one journal can accept the paper,ending the submission process.Thus the only possible cascade that can arise is one of rejection.In many situations cascades can be either positive-wherein all individuals adopt-or negative-wherein all individuals reject.Consider a teenager decid- ing whether or not to experiment with drugs.A strong motive for experimenting with drugs is the fact that friends are doing so.Con- versely,seeing friends reject drugs could help persuade a youth to stay clean

INFORMATIONAL CASCADES 995 Although the outcome may or may not be socially desirable,a rea- soning process that takes into account the decisions of others is en- tirely rational even if individuals place no value on conformity for its own sake.Imitation is,of course,an important social phenomenon, as has been documented by numerous studies in zoology,sociology, and social psychology.Our contribution is to model the dynamics of imitative decision processes as informational cascades. We examine (1)how likely it is that a cascade occurs,(2)how likely it is that the wrong cascade occurs(can a good paper be unpublish- able?),(3)how fashions change (why were college students of the 1980s pre-business "achievers,"whereas those in the 1960s flirted with "alternative cultures"?),and (4)how effective are public infor- mation releases (e.g.,a campaign to publicize the health effects of smoking). There are several related papers in which private information causes individuals to imitate the actions of others.In Conlisk's(1980) evolutionary model,optimizers-who incur a decision cost-coexist with imitators-who avoid this cost but make inferior decisions be- cause of observational lags.Welch(1992)examines the likelihood of cascades and optimal pricing in the market for initial public stock offerings.'Banerjee(in press)independently models"herd behavior" as cascades.Conceptually,our paper differs from Welch's and Baner- jee's in emphasizing the fragility of cascades with respect to different types of shocks;cascades can explain not only uniform behavior but also drastic change such as fads.8 The remainder of the paper is structured as follows.Section II presents the basic model,shows that cascades can often be mistaken, and provides conditions under which a cascade will almost surely start.It then examines how a few early individuals can have a dispro- portionate effect and how small parameter shifts can transform an imitator into a fashion dictator.Section III examines the effect of prior disclosure of public information and shows that cascades are fragile when new public information can arrive.Section IV discusses several examples.Section V shows how the possibility of changes in the underlying value of alternative decisions can lead to"fads,"that is,to drastic and seemingly whimsical swings in mass behavior without obvious external stimulus.Section VI concludes the paper. 7 Becker(1991)examines pricing decisions under demand externalities that might arise from informational sources. 8 In Scharfstein and Stein (1990)and Zwiebel(1990),conformity is an agency phe- nomenon.Scharfstein and Stein show that a manager may imitate the action of a preceding manager in order to improve his reputation for high ability.Zwiebel shows that relative performance evaluation may cause managers to adhere to inferior indus- try standards.Bhattacharya,Chatterjee,and Samuelson(1986)provide an interactive learning model of research and development

996 JOURNAL OF POLITICAL ECONOMY II.The Basic Model Information transmission among individuals can take many forms. For example,individuals may observe all other individuals'informa- tion,only the signals of predecessors,or only the actions of predeces- sors.Our analysis concentrates on the least informative case in which individuals observe only the actions of previous individuals.Since "ac- tions speak louder than words,"the information conveyed by actions may also be the most credible. A.A Specific Model For expositional clarity,we begin with a specific model.Assume that there is a sequence of individuals,each deciding whether to adopt or reject some behavior.Each individual observes the decisions of all those ahead of him.The ordering of individuals is exogenous and is known to all.3 All individuals have the same cost of adopting,C,which for now we set to l.The gain to adopting,V,is also the same for all individuals and is either zero or one,with equal prior probability .10 Individuals differ in their positions in the queue.Each individual privately observes a conditionally independent signal about value. Individual i's signal X;is either H or L,and H is observed with proba- bility p>if the true value is one and with probability 1-;if the true value is zero.Table 1 describes this binary signal case. We examine the special case of identically distributed signals(p:= p for all i).The expected value of adoption is just E[V]=y.1 (1 -y).0=Y,where y is the posterior probability that the true value is one.As a tie-breaking convention,an individual indifferent between adoption and rejection adopts or rejects with equal proba- bility. Thus the first individual adopts if his signal is H and rejects if it is L.The second individual can infer the first individual's signal from his decision.If the first individual adopted,the second individual adopts if his signal is also H.However,if his signal is L,the second individual computes the expected value of adoption(given one H and one L signal)to be 12.Being indifferent,he adopts with probability Similarly,if the first individual had rejected,the second individual rejects if his signal is also L and accepts with probability if his sig- nal is H.The third individual is faced with one of three situations: (1)both predecessors have adopted (in which case even an L signal induces him to adopt and thus creates an UP cascade),(2)both have 9 In Sec.IIC,we briefy discuss the determination of the order of moves. 10 The model also applies to the choice between two arbitrary actions,where V and C are the differences in values and in costs

INFORMATIONAL CASCADES 997 TABLE 1 SIGNAL PROBABILITIES Pr(X;=HV) Pr(Xi=L|V) V=1 1- V=0 1- Pi rejected (in which case even an H signal induces him to reject and thus creates a DowN cascade),or(3)one has adopted and the other rejected.In the last case,the third individual is in the same situation as the first individual:his expected value of adoption,based only on his predecessors'actions,is 2,and therefore his signal determines his choice.Should this come about,then a similar analysis shows that the fourth individual would be in the same situation as the second individual,the fifth as the third,and so forth. With this decision rule,we can derive the unconditional ex ante probabilities of an Up cascade,no cascade,or a DowN cascade after two individuals, 2p-p31-p+p 1-力+2 2 and 1-(中-p2)m2 1-(中-p2)n2 9 ,( -p)3 2 (1) after an even number of individuals n.1 Equation(1)shows that the closer p is to l,the later a cascade is likely to start.A reduction in p toward is equivalent to adding noise to the signal;at p=,the signal is uninformative.In other words,cascades tend to start sooner when individuals have more precise signals of the value of adoption.2 Moreover,according to(1),the probability of not being in a cascade falls exponentially with the number of individuals.Even for a very 11 After two individuals,no cascade occurs if there is one H and one L.This value can be calculated assuming V=1 (or 0).The occurrence of either HL or LH involves a coin flip,so the total probability is 'p(1-p)+p(1-p)=p(1 -p).For the other two values,it suffices to note that since these probabilities are not conditional on V,Pr(up)=Pr(DOwN)=[l -Pr(no cascade)].For the expressions in eq.(1),note that the probability of an Up cascade after four individuals is the probability of an up cascade after two individuals plus the probability of not being in a cascade after two individuals multiplied by the probability of an UP cascade after another two individuals. In contrast,the probability of not being in a cascade after four individuals is simply the probability of not being in a cascade after two individuals multiplied by the proba- bility of not being in a cascade after another two individuals. 1Specifically,higher-precision p raises the probability of histories that lead to the correct cascade
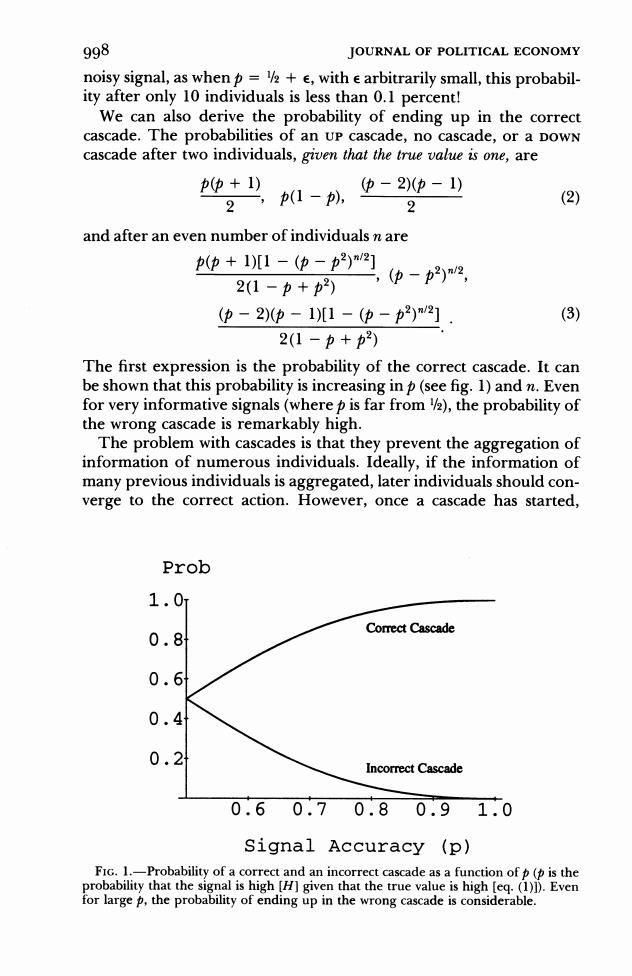
998 JOURNAL OF POLITICAL ECONOMY noisy signal,as whenp=+e,with e arbitrarily small,this probabil- ity after only 10 individuals is less than 0.1 percent! We can also derive the probability of ending up in the correct cascade.The probabilities of an Up cascade,no cascade,or a DowN cascade after two individuals,given that the true value is one,are 中+1) 2p1-, 中-2)中-1) 2 (2) and after an even number of individuals n are 中+1[1-(中-2)2] ,(中-2)2, 2(1-p+2) (中-2)(中-1)[1-(中-2)2] (3) 2(1-p+2) The first expression is the probability of the correct cascade.It can be shown that this probability is increasing in p(see fig.1)and n.Even for very informative signals(where p is far from )the probability of the wrong cascade is remarkably high. The problem with cascades is that they prevent the aggregation of information of numerous individuals.Ideally,if the information of many previous individuals is aggregated,later individuals should con- verge to the correct action.However,once a cascade has started, Prob 1.0 Correct Cascade 0.8 0.6 .41 2 Incorrect Cascade 0.60.70.80.91.0 Signal Accuracy (p) FIc.1.-Probability of a correct and an incorrect cascade as a function ofp(p is the probability that the signal is high [H]given that the true value is high [eq.(1)1).Even for large p,the probability of ending up in the wrong cascade is considerable

INFORMATIONAL CASCADES 999 actions convey no information about private signals;thus an individ- ual's action does not improve later decisions. Rogers and Shoemaker (1971)summarize research on the ability of outsiders(or"change agents")to bring about the adoption of desir- able innovations within communities.They offer the general proposi- tion that"change agent success is positively related to his efforts in increasing his clients'ability to evaluate innovations"(p.247).This is consistent with the prediction of this binary example that as the preci- sion of the signal,p,increases,a correct cascade starts with higher probability and,on average,earlier. It is instructive to compare the outcome in the previous-actions- observable(PAO)regime to that of the more informative previous- signals-observable(PSO)regime.In the binary signal case,PAO leads to a more uniform outcome.Following any given sequence of signal realizations,the two regimes lead to precisely identical outcomes,un- til a cascade begins in the PAO regime.However,in the PAO regime, after a cascade starts it is never reversed.In the PSO regime,even if an individual does not follow his private signal,it joins the common pool of knowledge.Hence,a long enough series of opposing signals will eventually cause people's behavior to switch.Thus the PAO leads to greater uniformity.We shall argue in Section V that this uniformity is brittle:small shocks can easily shift the behavior of many indi- viduals. B.A General Model We now show that under mild assumptions on the signals and values, cascades will always arise.Let there be a sequence of individuals i 1,2,...,n,...,each deciding whether to adopt some behavior or to reject it.Each individual observes the decisions of all those ahead of him.The order of individuals is exogenous and is known to all.All individuals have the same cost of adopting,C,and gain to adopting,V.The gain V has a finite set of possible values,v<v2 <..<vs,and the decision is not trivial (v<C<vs).The prior probability that V =v is denoted We use the concept of perfect Bayesian equilibrium.Since an indi- vidual's payoffs do not depend on what later individuals do,there is no incentive to make an out-of-equilibrium move to try to influence a later player.Thus,without loss of generality,we assume that if any player is observed to deviate from the equilibrium,either by rejecting when he should have adopted regardless of his signal realization or by adopting when he should have rejected regardless,then subsequent individuals have the same beliefs as though he had chosen his correct (equilibrium)action

1000 JOURNAL OF POLITICAL ECONOMY Individuals differ not only by their positions in the queue but by the signals they privately observe.Each individual i observes one of a conditionally independent and identically distributed sequence of signals X;with possible values x0 for all g and l.Let P be the cumulative distribution of X;given V=v,that is, P=Pr(,=xlV=-之r Let J;be the set of signal realizations that lead individual i to adopt. His decision communicates to others that he observed either a signal in the set J;or its complement.IfJi=x1,x2,...,xg}or if Ji is empty,then individual i's action conveys no information about his realization. DEFINITION.An informational cascade occurs if an individual's ac- tion does not depend on his private information signal. If an individual i is in a cascade,then his action conveys no informa- tion and individual i+1 draws the same inference from all previous actions.Since the signal Xi+is drawn from the same distribution as Xi,individual i+1 is also in a cascade.Thus,by induction,all individ- uals after i are in a cascade.Consequently,a cascade once started will last forever,even if it is wrong.We shall see later that this fallibility causes cascades to be fragile.For instance,if individuals'signals have different distributions,as in Section IIC,if public information is re- vealed at a later date,as in Section IIIA,or if underlying values can change,as in Section V,then cascades can easily be broken. Let a;be individual i's action (adopt or reject)and let A;=(a1,a2,..., a,)represent the history of actions taken by individuals 1,2,...,i. Given history A:-1,leti(A:-1,a)be the set of signal realizations that lead individual i to choose action a;.Then individual n l's condi- tional expectation of V given his own signal realization x and the history An is Vn+1(cgAn)=E[VlXn+1=xg,X,∈J(A:-,a),for alli≤l. Individual n 1 adopts if1s V+1(A)C.Therefore,the infer- ence drawn from n I's action a+1 is that X+1En+(An,an+), where n+1(An,adopt)=[x such that V+1(A)=Ch, n+1(An,reject)={x such that V+1(xA)<C). is Since we are no longer restricting ourselves to a symmetric example,we use a tie-breaking assumption (indifferent individuals adopt)slightly different from the one in the previous section (indifferent individuals randomize).This reduces notation but not generality

INFORMATIONAL CASCADES 1001 We impose two regularity conditions.The first is that the condi- tional distributions Pr(XilV =v)are ordered by the monotone likeli- hood ratio property.4 This ensures that if an individual observes a higher signal realization,he infers that the value of adoption is higher (in a first-order stochastic dominance sense). AssUMPTIoN 1.Monotone likelihood ratio ordering.-For all l<S, L≥for all<R, Pg+1.1Pg+1,1+1 with strict inequality for at least one g. Assumption 1 ensures that the conditional expectation of each indi- vidual increases in his signal realization.Thus if individual i is not in a cascade and he adopts,later individuals conclude that X;=x for some q.If i does not adopt,then the conclusion is that X:< The second assumption ensures that if individuals learn enough about value by observing predecessors,then they are not indifferent between adopting and rejecting.15 ASSUMPTION2.No long-run ties..一M≠C for all, A major result of this section is that a cascade eventually begins. Suppose that an individual late in the sequence is still making a deci- sion based on his own information.Then the decisions of earlier individuals convey some information about their signals.If this indi- vidual is far enough down the line,then,by the strong law of large numbers,with probability close to one he can infer the true value of adoption with almost perfect certainty.But then his own signal contributes arbitrarily little to his information set,and he acts ac- cording to the information conveyed by the actions of previous indi- viduals.Therefore,he ignores his private information and starts a cascade. PRoposrTIoN 1.If assumptions 1 and 2 hold,then as the number of individuals increases,the probability that a cascade eventually starts approaches one. While we have shown that cascades must eventually occur,perhaps the more interesting point is that they will often be wrong.16 In an 1 The monotone likelihood ratio property is a standard assumption in models in which inferences must be drawn from a noisy signal.Milgrom(1981)provides a presen- tation and applications. i5 It is a mild assumption.If v,v,...,vs and C are drawn randomly from any nonatomic probability measure,assumption 2 is satisfied with probability one.This assumption prevents asymptotic indifference but is not a tie-breaking convention. 16 The proof of proposition 1 is based on the idea that many observations of informa- tive actions would lead with high probability to nearly perfect knowledge of value. Thus with high probability a cascade must start at or before such a point,but this cascade will often be an incorrect one that started much earlier.As fig.I in Sec.IIA shows,the probability of an incorrect cascade in the specific model can be close to.5 if the signal is noisy enough