
上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY Engineering Thermodynamics I Lectures 15 Spring,3/25/2019 Prof.,Dr.Yonghua HUANG 强 月是A http://cc.sjtu.edu.cn/G2S/site/thermo.html 1日G
Engineering Thermodynamics I Lectures 15 Spring, 3/25/2019 Prof., Dr. Yonghua HUANG http://cc.sjtu.edu.cn/G2S/site/thermo.html
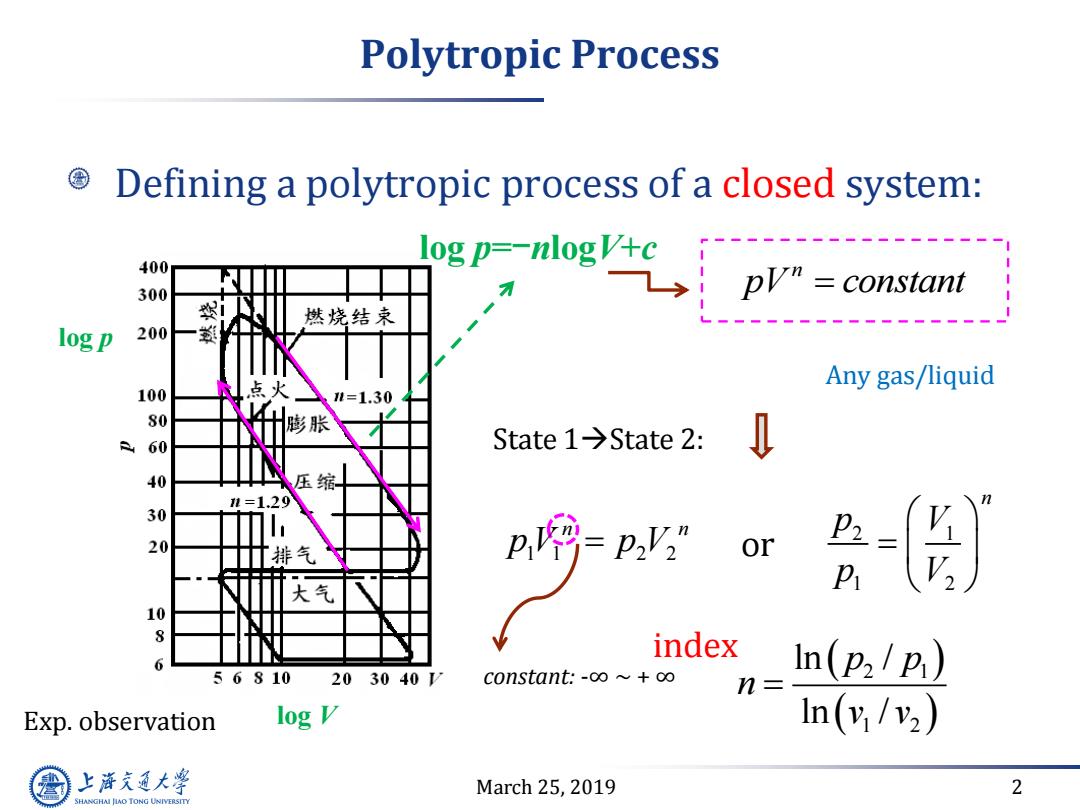
Polytropic Process Defining a polytropic process of a closed system: 400 300 燃烧结束 Logog'气,p=consn log p 200 点火 Any gas/liquid 100 =1.30 60 膨胀 State1→State2: 40 压缩 1=1.29 30 20 排气 p网p,”or 大气 10 8 index 6 56810 203040V constant.-o∞~+o∞ In(p2/p) n= Exp.observation log V In(v/v2) 上游充通大 March 25,2019 2 SHANGHAI JIAO TONG UNIVERSITY
March 25, 2019 2 Polytropic Process Defining a polytropic process of a closed system: n pV constant constant: -∞ ~ + ∞ State 1State 2: 1 1 2 2 n n p V p V or 2 1 1 2 n p V p V log p Exp. observation log V 2 1 1 2 ln / ln / p p n v v Any gas/liquid log p=-nlogV+c index
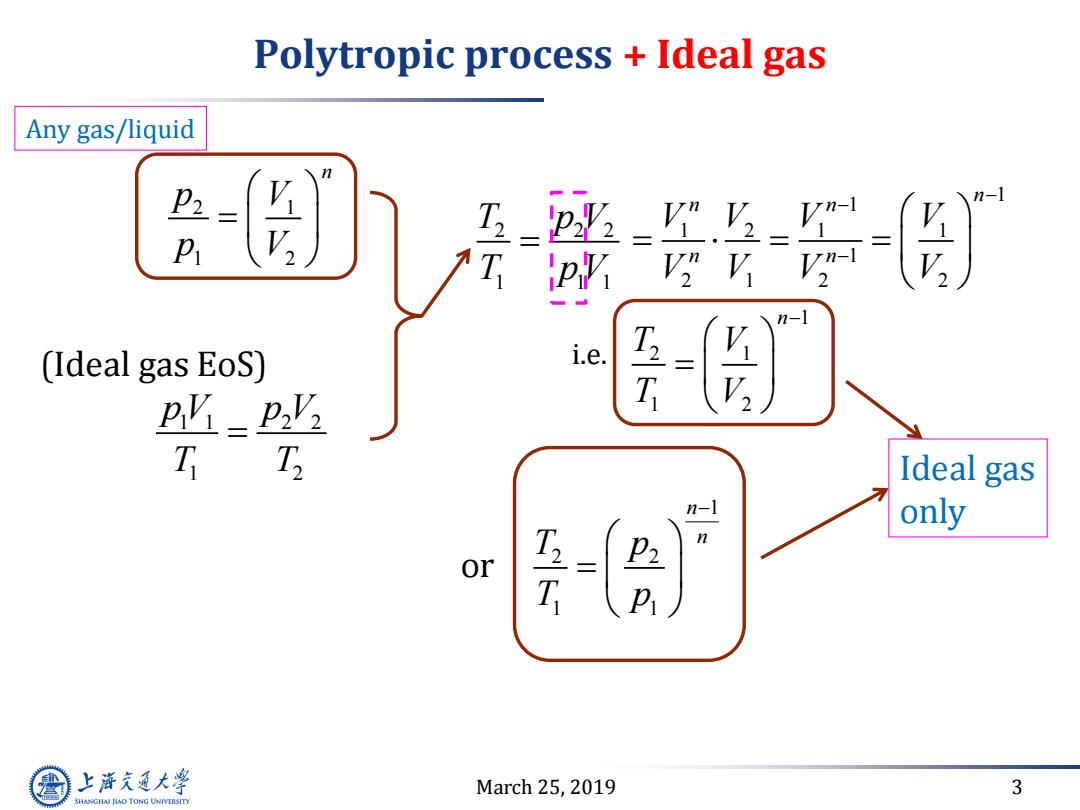
Polytropic process Ideal gas Any gas/liquid P2 P V 1- (Ideal gas EoS) i.e. pyPVz T Ideal gas n-1 only or P2 上游充通大学 March 25,2019 3 SHANGHAI JIAO TONG UNIVERSITY
March 25, 2019 3 Polytropic process + Ideal gas 1 1 2 2 1 2 pV p V T T (Ideal gas EoS) 2 2 2 1 1 1 T p V T pV 1 2 2 1 1 n n T p T p 2 1 1 2 n p V p V or Ideal gas only 1 1 1 2 1 1 1 2 1 2 2 n n n n n V V V V V V V V Any gas/liquid 1 2 1 1 2 n T V T V i.e

Four particular cases n=0 D=const. (isobaric process;constant pressure process) n=1 pv =const. (isothermal process;constant temperature process) pV"=p2'2” n=K DyA =const. (isentropic process;reversible adiabatic process) For ideal gas:adiabatic index K =k(specific heat ratio) n=士o∞ V=const. (isometric/isochoric process;constant volume process) 上游充通大学 March 25,2019 4 SHANGHAI JIAO TONG UNIVERSITY
March 25, 2019 4 Four particular cases 1 1 2 2 n n p V p V n p 0 const. n pv 1 const. n pv const. n v const. (isobaric process; constant pressure process) (isometric/isochoric process; constant volume process) (isentropic process; reversible adiabatic process) (isothermal process; constant temperature process) For ideal gas: adiabatic index = k (specific heat ratio)
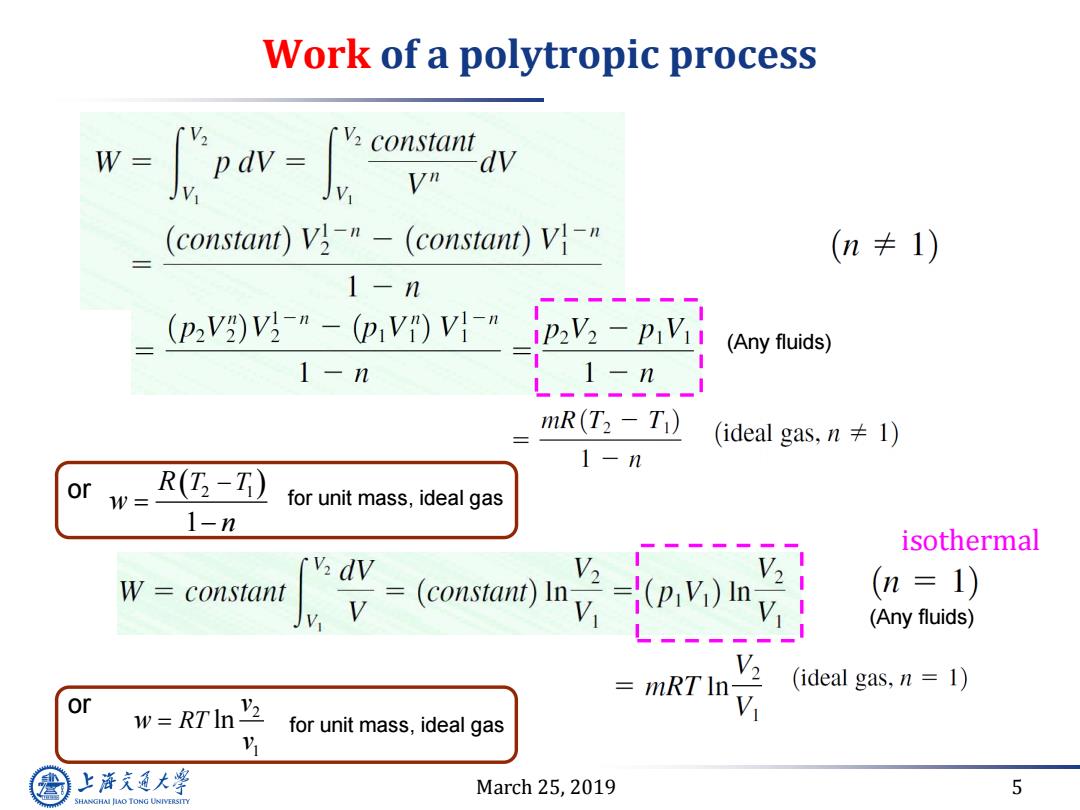
Work of a polytropic process w- Vn (constant)Vg-"-(constant0)V-n (n≠1) 1-n (p2V)vI-"-(piV)VI-" (Any fluids) 1-n mR(T2-T) (ideal gas,.n≠1) 1-n or w= R(T-T) for unit mass,ideal gas 1-n isothermal [v:dv W constant v= (n=1) (Any fluids) (ideal gas,n 1) or w-RTn业 mRT In V for unit mass,ideal gas y 上降文通大学 March 25,2019 5 SHANGHAI JIAO TONG UNIVERSITY
March 25, 2019 5 Work of a polytropic process isothermal (Any fluids) (Any fluids) 2 1 1 R T T w n or for unit mass, ideal gas for unit mass, ideal gas 2 1 RT ln v w v or
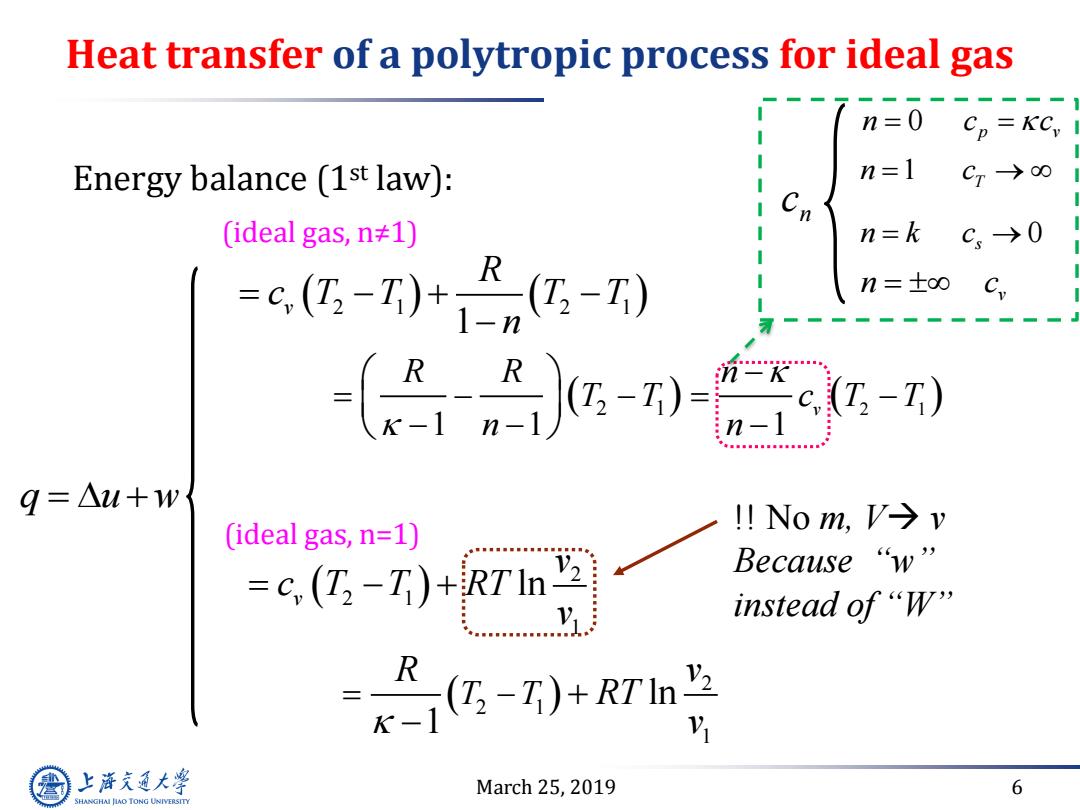
Heat transfer of a polytropic process for ideal gas n=0 Cp =KCy Energy balance (1st law): n=1 Cr→0 (ideal gas,n≠1) n=k C,→0 -c西-)-0 n=士oo C --0 n- G-T) n-1 q=△u+w !No m,V→v (ideal gas,n=1) =c (G-T)+RTI Because“w' instead of“W" =x是g-)+rh R V 上游充通大 March 25,2019 6 SHANGHAI JIAO TONG UNIVERSITY
March 25, 2019 6 Heat transfer of a polytropic process for ideal gas 2 1 2 1 2 1 2 1 1 1 1 1 v v R R n T T c T T n n R c T T T T n Energy balance (1st law): (ideal gas, n≠1) q u w n c 0 p v n c c 1 T n c 0 s n k c v n c (ideal gas, n=1) 2 2 1 1 2 2 1 1 ln ln 1 v T T v c T T RT v R v RT v !! No m, V v Because “w” instead of “W

Energy relationship w/q of polytropic process …} (ideal gas,n≠1) R W K-1 0 >0 W nK <0 w<0 膨胀,放热;压缩,吸热 K-n 9 Expan.,Reject;Compr.,Absorb 上游通大学 March 25,2019 7 SHANGHAI JIAO TONG UNIVERSITY
March 25, 2019 7 Energy relationship w/q of polytropic process 1 2 1 2 2 1 1 1 1 1 v v R w T T c T T n n n q c T T n 0 0 1 q w n n w 1 q n 0 0 1 q w n n (ideal gas, n≠1) 膨胀,吸热; 压缩, 放热 Expan., Absorb; Compr., Reject 膨胀,放热; 压缩, 吸热 Expan.,Reject; Compr., Absorb
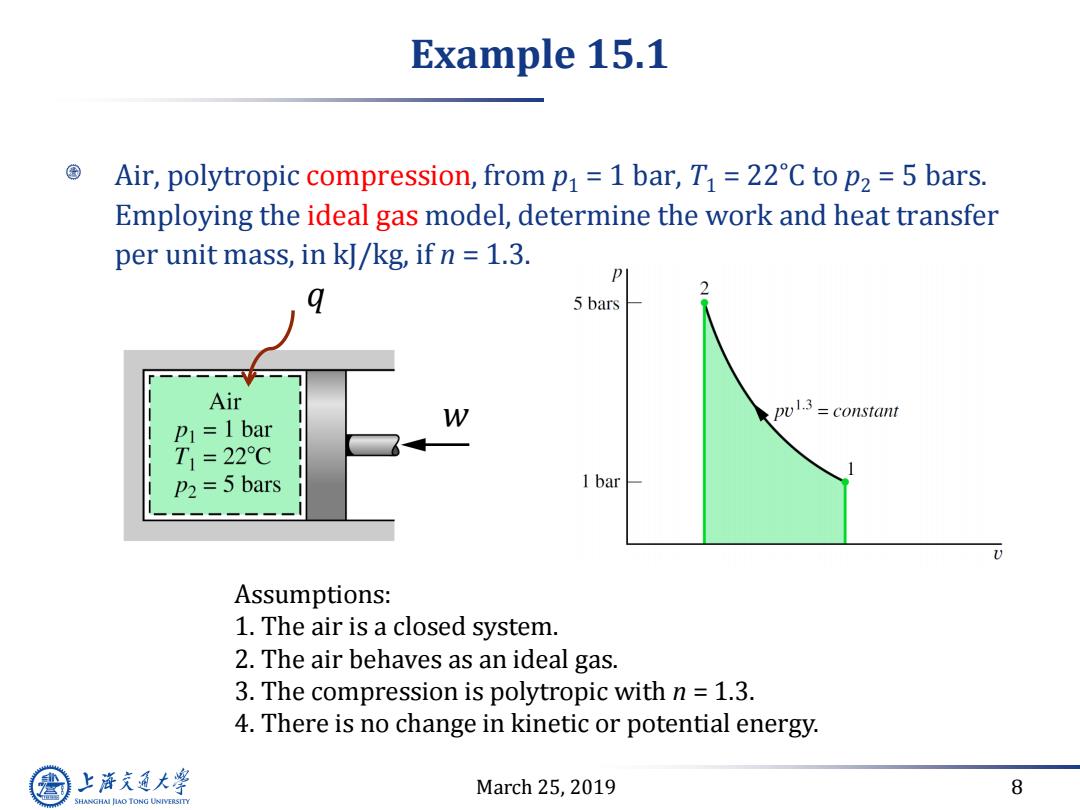
Example 15.1 Air,polytropic compression,from p=1 bar,T1=22C to p2 =5 bars. Employing the ideal gas model,determine the work and heat transfer per unit mass,in kJ/kg,if n 1.3. 5 bars Air W pul3=constant P1=1 bar T1=22℃ P2=5 bars 1 bar Assumptions: 1.The air is a closed system. 2.The air behaves as an ideal gas. 3.The compression is polytropic with n 1.3. 4.There is no change in kinetic or potential energy. 上游充通大 March 25,2019 8 SHANGHAI JLAO TONG UNIVERSITY
March 25, 2019 8 Example 15.1 Air, polytropic compression, from p1 = 1 bar, T1 = 22˚C to p2 = 5 bars. Employing the ideal gas model, determine the work and heat transfer per unit mass, in kJ/kg, if n = 1.3. q w Assumptions: 1. The air is a closed system. 2. The air behaves as an ideal gas. 3. The compression is polytropic with n = 1.3. 4. There is no change in kinetic or potential energy
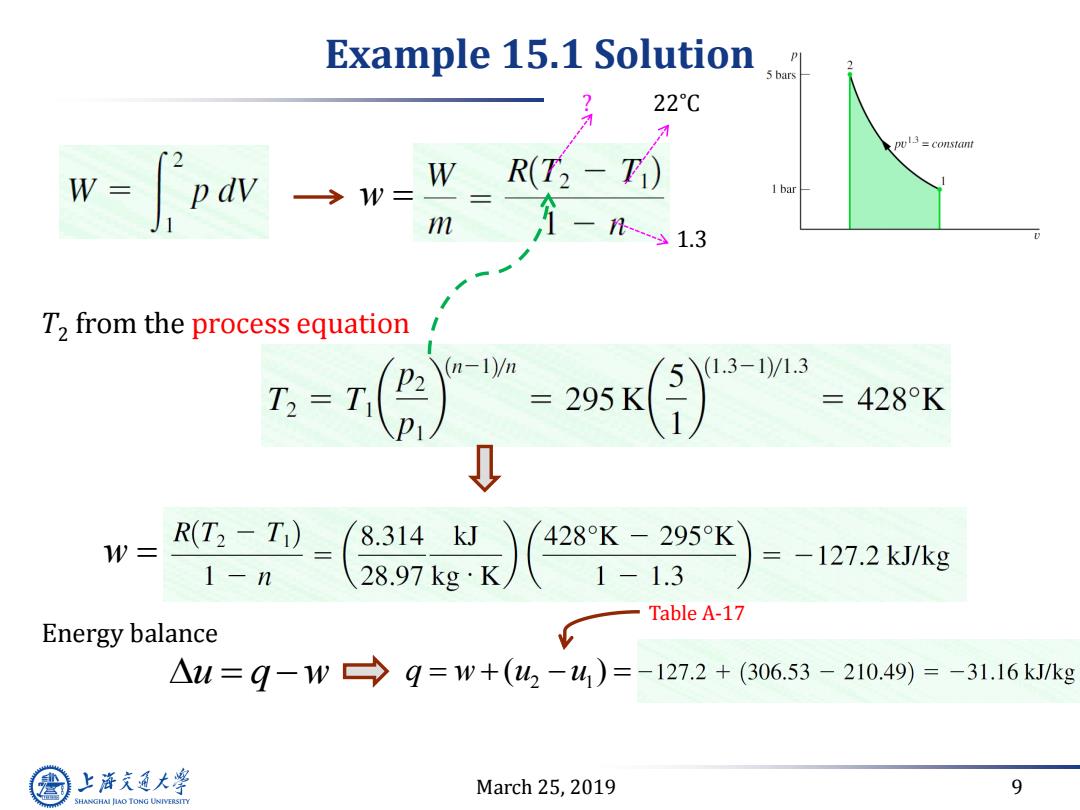
Example 15.1 Solution P s bars 22C pul3 =constant w-fow →w= W R(T2-F) 1 bar m -313 T2 from the process equation (n-1)/m (1.3-1)/1.3 =295K =428K W= R(T2-T) 8.314kJ 428K-295K =-127.2kJ/kg 1-n 1-1.3 Table A-17 Energy balance △2u=q-1w→9=w+(42-4)=-127.2+(306.53-210.49)=-31.16kg 上游充通大 March 25,2019 9 SHANGHAI JIAO TONG UNIVERSITY
March 25, 2019 9 Example 15.1 Solution 22˚C 1.3 ? T2 from the process equation Energy balance u q w w w 2 1 q w u u ( ) Table A-17

Reversible polytropic process on p-v diagram Reversible adiabatic process py"= const T dv → 业 tn =0 p v n=0 Slope (n=0) 0 n=1 → =-n P (n=1) 1n=0 n=k (n=K) 一 n=±oo 00 上游充通大 March 25,2019 10 SHANGHAI JIAO TONG UNIVERSITY
March 25, 2019 10 Reversible polytropic process on p-v diagram . n pv const d d 0 p v n p v n p p n v v Slope n v p n v p n n ( ) ( 1) ( 0) 0 Reversible adiabatic process