
上游充通大学 SHANGHAI JIAO TONG UNIVERSITY Engineering Thermodynamics I Lecture 28 Chapter 7 Entropy (Section 7.1) Spring,4/16/2019 福 Prof.,Dr.Yonghua HUANG 月是 http://cc.sjtu.edu.cn/G2S/site/thermo.html 1日G
Engineering Thermodynamics I Lecture 28 Spring, 4/16/2019 Prof., Dr. Yonghua HUANG Chapter 7 Entropy (Section 7.1) http://cc.sjtu.edu.cn/G2S/site/thermo.html

Chapter objective Up to this point,2nd law concerning systems undergoing thermodynamic cycles 国 To introduce means for analyzing systems using 2nd law for processes 国 To introduce entropy 上游充通大学 April 16,2019 2 SHANGHAI JIAO TONG UNIVERSITY
April 16, 2019 2 Chapter objective To introduce means for analyzing systems using 2nd law for processes To introduce entropy Up to this point, 2nd law concerning systems undergoing thermodynamic cycles
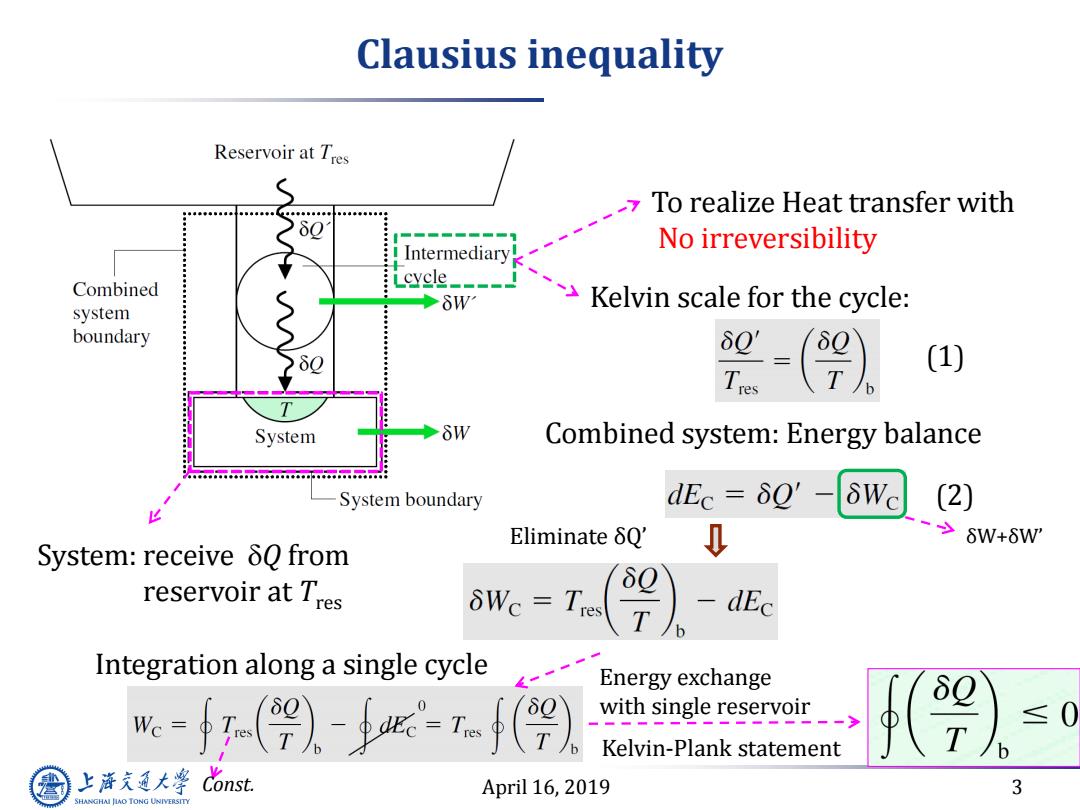
Clausius inequality Reservoir at Tres To realize Heat transfer with No irreversibility Intermediary! Combined cycle Kelvin scale for the cycle: system boundary 60' Tres (1) System Combined system:Energy balance w.o.baacoobaace...a.a.ceobeacoooo System boundary dEc=δQ' δWc (2) EliminateδQ' ->6W+6W' System:receive 80 from 0 reservoir at Tres δ0 WC =Tres -dEc Integration along a single cycle Energy exchange Wc with single reservoir Kelvin-Plank statement 上海充通大学 Cons April 16,2019 3 SHANGHAI JIAO TONG UNIVERSITY
April 16, 2019 3 Clausius inequality System: receive Q from reservoir at Tres To realize Heat transfer with No irreversibility Kelvin scale for the cycle: Combined system: Energy balance Eliminate δQ’ δW+δW’ Integration along a single cycle Const. Energy exchange with single reservoir Kelvin-Plank statement (1) (2)

Clausius inequality boundary Reservoir at Tres 80 ≤ T Intermediary cycle_- Kelvin-Plank statement Combined system δW --A corollary of the 2nd law boundary Applicable to any cycle System δW "="no irreversibility within the system System boundary “<“:internal irreversibilities are present No irreversibility for irreversibility only the intermediary cycle within the system 上游充通大 April 16,2019 4 SHANGHAI JIAO TONG UNIVERSITY
April 16, 2019 4 Clausius inequality -- A corollary of the 2nd law Applicable to any cycle No irreversibility for the intermediary cycle “=”: no irreversibility within the system “<“: internal irreversibilities are present Kelvin-Plank statement irreversibility only within the system boundary

General form of Clausius inequality (9-园 "strength"or degree of the inequality Ocyele= 0 no irreversibilities present within the system Ceycle irreversibilities present within the system Ceycle <O impossible 上游充通大学 April 16,2019 5 SHANGHAI JLAO TONG UNIVERSITY
April 16, 2019 5 General form of Clausius inequality “strength” or degree of the inequality

Recall definition of property 1m3 d 3 3m3 Example:the cyclic integral of volume (or any other property)is zero. 1m3 A quantity whose cyclic integral is zero depends on the state only and not the process 中dV=AVeycle=0 path,and thus it is a property. 上游充通大 April 16,2019 6 SHANGHAI JLAO TONG UNIVERSITY
April 16, 2019 6 Recall definition of property Example: the cyclic integral of volume (or any other property) is zero. ↓ A quantity whose cyclic integral is zero depends on the state only and not the process path, and thus it is a property

Entropy definition 2 A quality is a property,if,and only if,its change in value between two states is independent of the process. Two cycles: Cycle #1:"1-A-2"(internal reversible) +"2-C-1"(internal reversible) (9)。+(2)= Cycle #2:"1-B-2"(internal reversible) +"2-C-1"(internal reversible) 1 (》+(9)。=f… (9)-() 上游究通大学 April 16,2019 7 SHANGHAI JLAO TONG UNIVERSITY
April 16, 2019 7 Entropy definition A quality is a property, if, and only if, its change in value between two states is independent of the process. Two cycles: Cycle #1: “1-A-2” (internal reversible) + “2-C-1” (internal reversible) Cycle #2: “1-B-2” (internal reversible) + “2-C-1” (internal reversible)
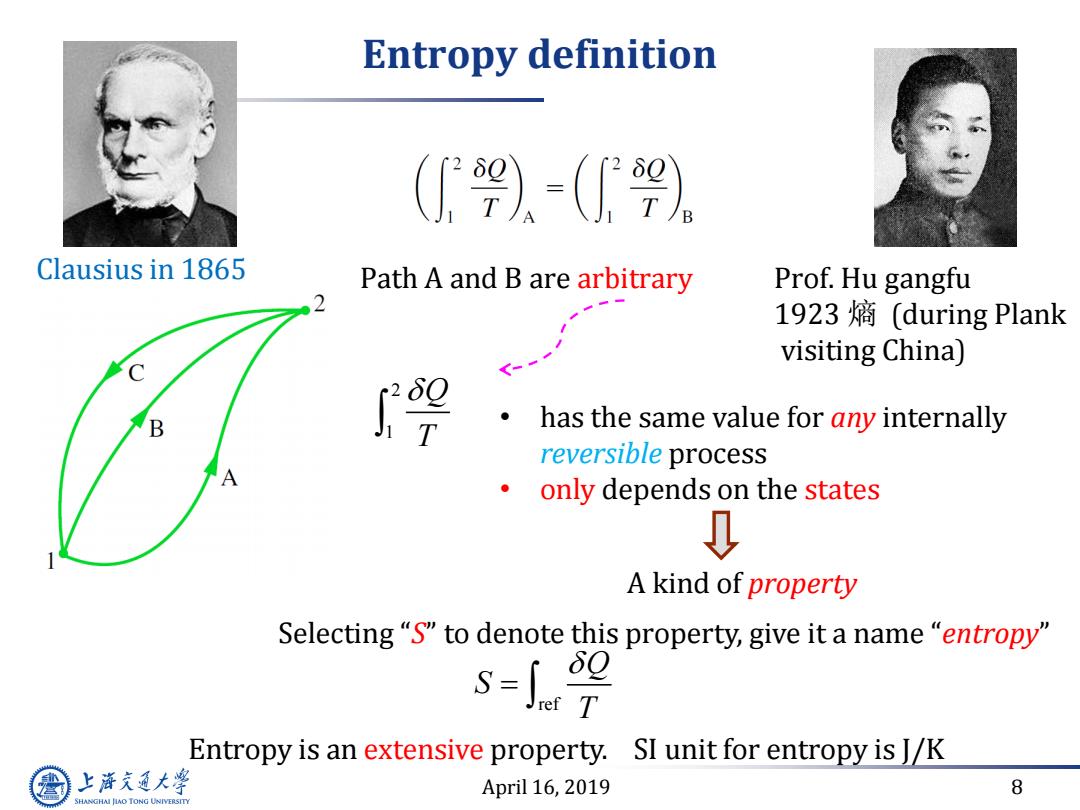
Entropy definition ()=() Clausius in 1865 Path A and B are arbitrary Prof.Hu gangfu 1923熵(during Plank visiting China) has the same value for any internally reversible process A only depends on the states 0 A kind of property Selecting "S"to denote this property,give it a name "entropy 99 Entropy is an extensive property. SI unit for entropy is J/K 上游充通大学 April 16,2019 8 SHANGHAI JLAO TONG UNIVERSITY
April 16, 2019 8 Entropy definition Path A and B are arbitrary 2 1 Q T • has the same value for any internally reversible process • only depends on the states A kind of property Selecting “S” to denote this property, give it a name “entropy” Entropy is an extensive property. Clausius in 1865 SI unit for entropy is J/K ref Q S T Prof. Hu gangfu 1923 熵 (during Plank visiting China)
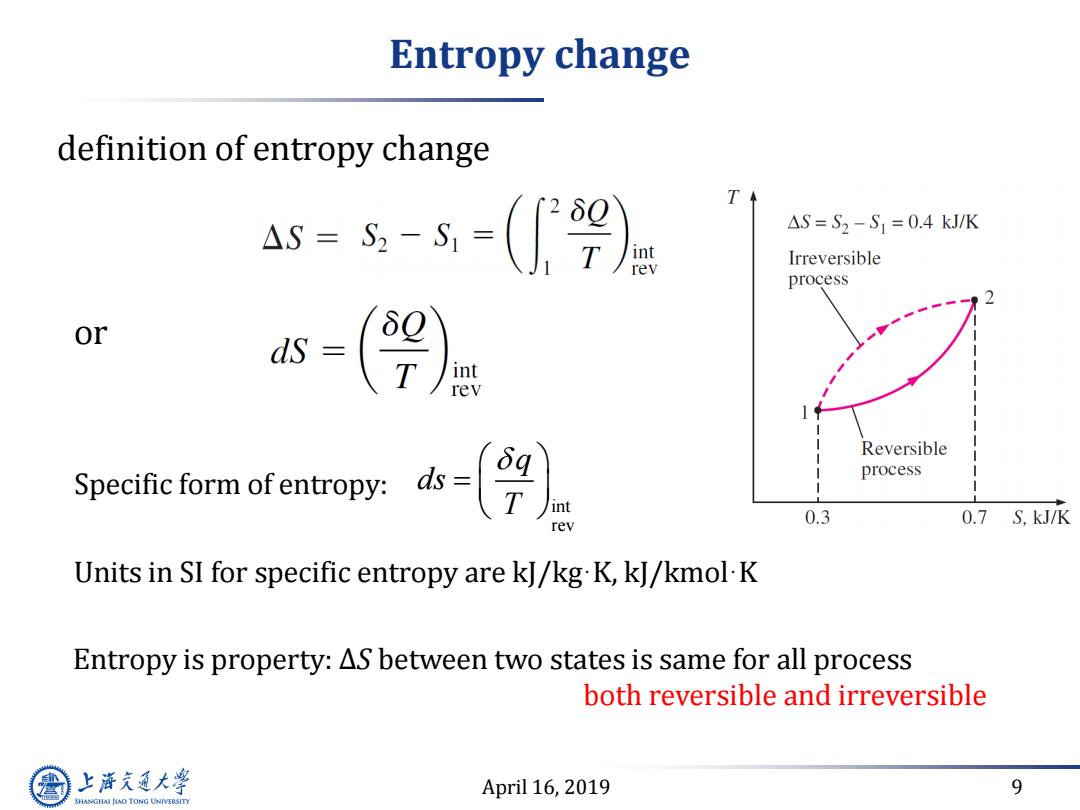
Entropy change definition of entropy change 4s=s-=(9) T △S=S2-S1=0.4kJ/K int rev Irreversible process or T int rev Reversible Specific form ofentropy:ds- process rev 0.3 0.7 S,kJ/K Units in SI for specific entropy are kJ/kg K,kJ/kmol-K Entropy is property:AS between two states is same for all process both reversible and irreversible 上游通大学 April 16,2019 9 SHANGHAI JLAO TONG UNIVERSITY
April 16, 2019 9 Entropy change definition of entropy change Units in SI for specific entropy are kJ/kg·K, kJ/kmol·K or Specific form of entropy: int rev q ds T Entropy is property: ∆S between two states is same for all process both reversible and irreversible

Sign/Direction of dS related with oQ 82ner>0, then ds >0 ds (9 82ner=0, then dS=0 82net<0, then dS 0 dS=0:The reversible,adiabatic process is called an isentropic process. 上游充通大学 April 16,2019 10 SHANGHAI JLAO TONG UNIVERSITY
April 16, 2019 10 Sign/Direction of dS related with δQ dS = 0: The reversible, adiabatic process is called an isentropic process. Q then dS Q then dS Q then dS net net net 0 0 0 0 0 0 , ,