
Engineering Thermodynamics I Lecture 39-40 Chapter 10 Vapor and Combined Power Systems Spring,5/4/2018 Prof.,Dr.Yonghua HUANG http://cc.sjtu.edu.cn/G2S/site/thermo.html 上游充通大学 May4,2018 1 SHANGHAI JLAO TONG UNIVERSITY
May 4, 2018 1 Engineering Thermodynamics I Lecture 39-40 Spring, 5/4/2018 Prof., Dr. Yonghua HUANG Chapter 10 Vapor and Combined Power Systems http://cc.sjtu.edu.cn/G2S/site/thermo.html
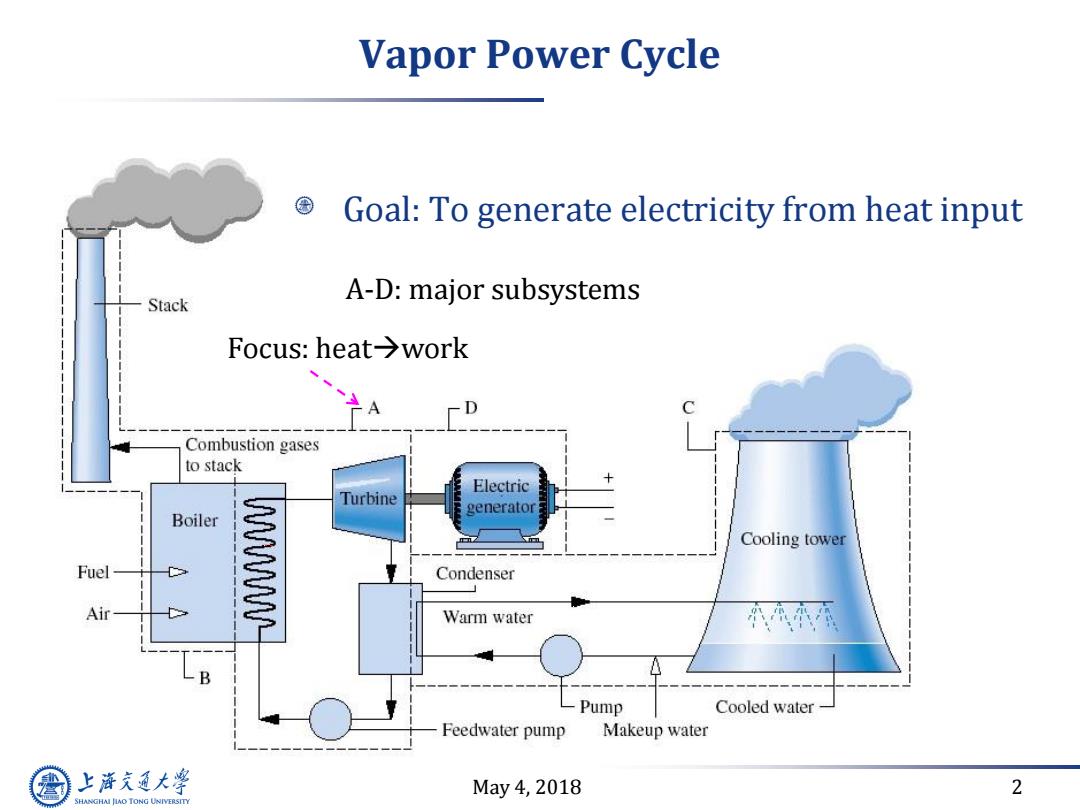
Vapor Power Cycle Goal:To generate electricity from heat input Stack A-D:major subsystems Focus::heat→work D C Combustion gases to stack Electric Turbine generator Boiler Cooling tower Fuel W Condenser Air Warm water B Pump Cooled water Feedwater pump Makeup water 上游充通大学 May4,2018 2 SHANGHAI JIAO TONG UNIVERSITY
May 4, 2018 2 Vapor Power Cycle Goal: To generate electricity from heat input A-D: major subsystems Focus: heatwork
Continue Vapor Power Cycle Heat Input Sources: Fossil fuels (oil,coal,natural gas) Nuclear fission/fussion ●Geothermal 。Solar radiation --->Renewable,low grade energy ·Garbage/Trash Cycle Working Fluid: ·Water/Steam Vaporization/Condensation Environmental Issues: ●Air pollution ·Thermal pollution ·Waste products ·Safety 上游通大学 May4,2018 3 SHANGHAI JLAO TONG UNIVERSITY
May 4, 2018 3 Continue Vapor Power Cycle Heat Input Sources: • Fossil fuels (oil, coal, natural gas) • Nuclear fission/fussion • Geothermal • Solar radiation • Garbage/Trash Cycle Working Fluid: • Water/Steam Environmental Issues: • Air pollution • Thermal pollution • Waste products • Safety Vaporization/Condensation Renewable, low grade energy
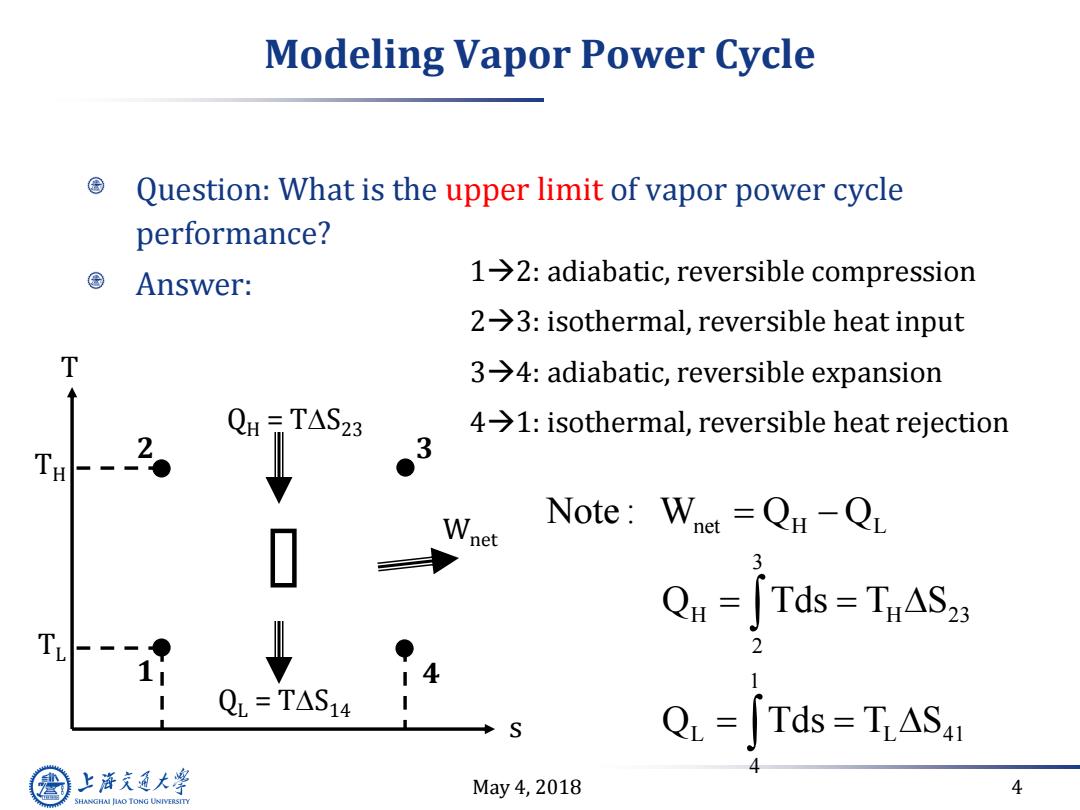
Modeling Vapor Power Cycle Question:What is the upper limit of vapor power cycle performance? 国 Answer: 1→2:adiabatic,reversible compression 2→3:isothermal,reversible heat input T 3→4:adiabatic,reversible expansion QH-TAS23 4>1:isothermal,reversible heat rejection 2。 3 ● Wnet Note:Whet =Qu-QL Qu=[Tds=TnASz T. 14 QL=TAS14 QL =Tds TiASa 上游充通大 May4,2018 4 SHANGHAI JLAO TONG UNIVERSITY
May 4, 2018 4 Modeling Vapor Power Cycle Question: What is the upper limit of vapor power cycle performance? Answer: 12: adiabatic, reversible compression 23: isothermal, reversible heat input 34: adiabatic, reversible expansion 41: isothermal, reversible heat rejection net H L 3 H H 23 2 1 L L 41 4 Note : W Q Q Q Tds T S Q Tds T S 1 2 3 4 s T QH = TS23 QL = TS14 Wnet TH TL
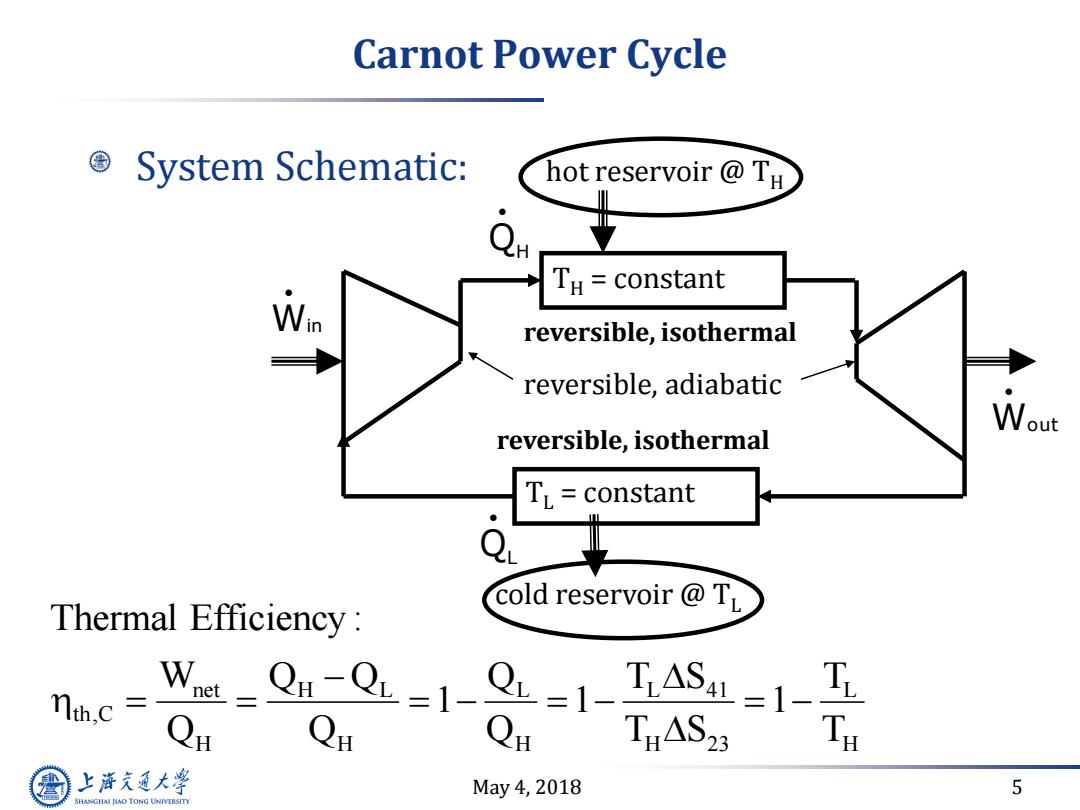
Carnot Power Cycle System Schematic: hot reservoir TH e TH constant reversible,isothermal reversible,adiabatic Wout reversible,isothermal TL=constant Q cold reservoir TL Thermal Efficiency: nth.c =Qn-QL=1-QL=1-TASL=1-T THAS2 上降文通大学 May4,2018 5 SHANGHAI JIAO TONG UNIVERSITY
May 4, 2018 5 Carnot Power Cycle System Schematic: hot reservoir @ TH TH = constant cold reservoir @ TL TL = constant QH QL Win Wout reversible, isothermal reversible, isothermal net H L L L 41 L th,C H H H H 23 H Thermal Efficiency : W Q Q Q T S T 1 1 1 Q Q Q T S T reversible, adiabatic

Continue Carnot Power Cycle Example 39.1: Given:TH =500 K and TL 300 K Find:Thermal efficiency of Carnot Cycle Solution:nth.c=0.4 1.0 b Question: How to implement the 0.5 Carnot Power Cycle with a real working fluid? 0 a 298100020003000 TH(K) 上游究通大学 May4,2018 6 SHANGHAI JLAO TONG UNIVERSITY
May 4, 2018 6 Continue Carnot Power Cycle Example 39.1: Given: TH = 500 K and TL = 300 K Find: Thermal efficiency of Carnot Cycle Solution: th,C = 0.4 Question: How to implement the Carnot Power Cycle with a real working fluid?
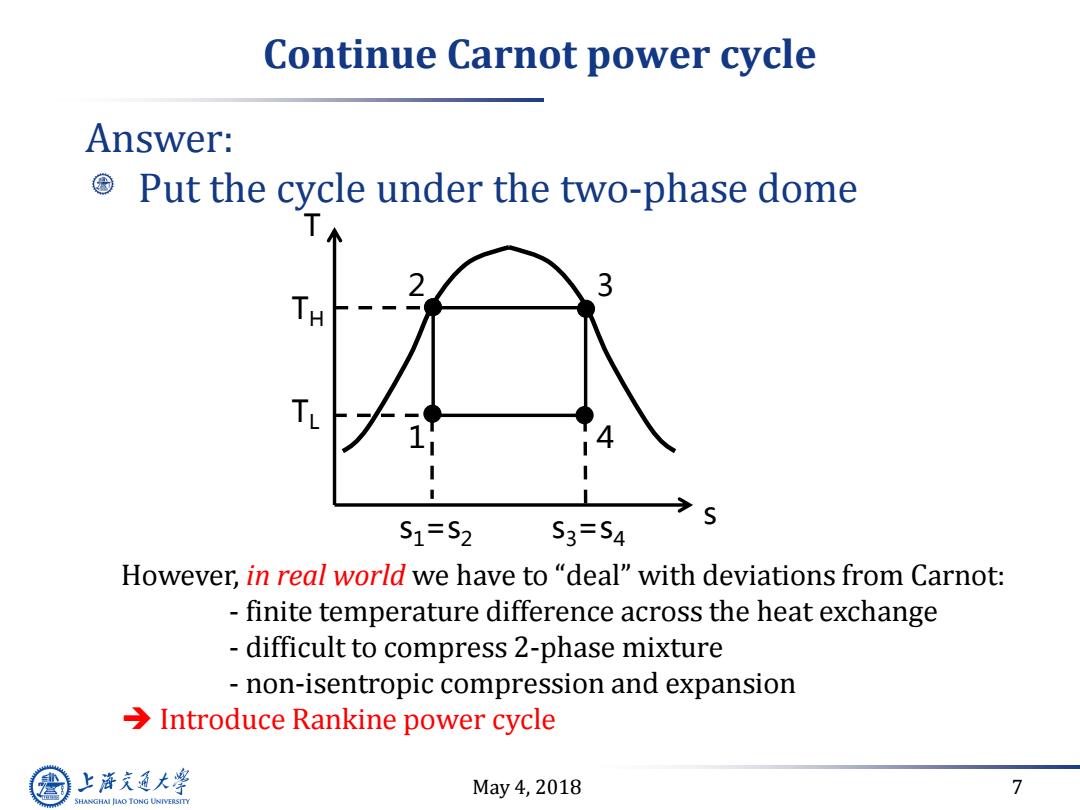
Continue Carnot power cycle Answer: Put the cycle under the two-phase dome TH 4 S1=S2 S3=S4 However,in real world we have to "deal"with deviations from Carnot: finite temperature difference across the heat exchange difficult to compress 2-phase mixture non-isentropic compression and expansion >Introduce Rankine power cycle 上游充通大 May4,2018 7 SHANGHAI JLAO TONG UNIVERSITY
May 4, 2018 7 Continue Carnot power cycle Answer: Put the cycle under the two-phase dome However, in real world we have to “deal” with deviations from Carnot: - finite temperature difference across the heat exchange - difficult to compress 2-phase mixture - non-isentropic compression and expansion Introduce Rankine power cycle T s 1 2 3 4 s1=s2 s3=s4 TH TL
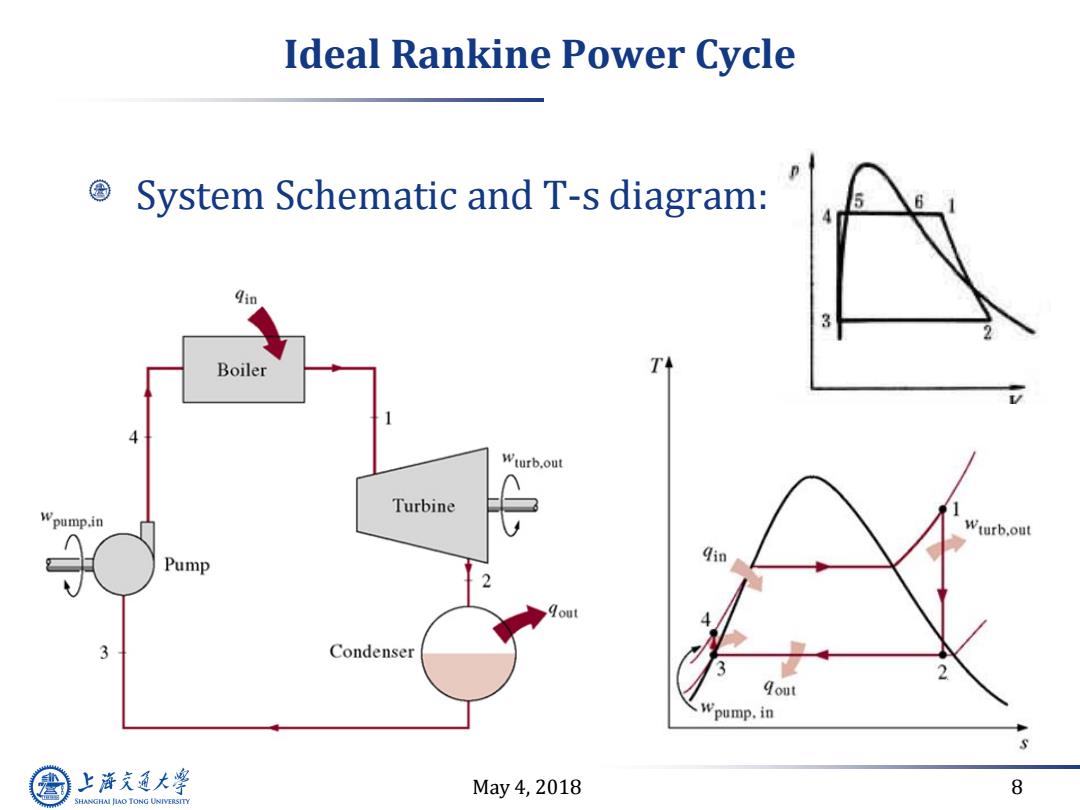
Ideal Rankine Power Cycle System Schematic and T-s diagram: qin 3 Boiler T Wturb.out Turbine 1 Wpump.in Wturb.out Pump Qin 2 3 Condenser 2 qout pump.in 上游充通大 May4,2018 8 SHANGHAI JIAO TONG UNIVERSITY
May 4, 2018 8 Ideal Rankine Power Cycle System Schematic and T-s diagram:

Continue Ideal Rankine Power Cycle Define ideal Rankine power cycle: .Neglect the finite temperature difference of heat exchanger →△THx=0,TBoiler=TH and Tcond=TL Isentropic expansion and pumping processes >S1=s2 and s3=s4 Difference between ideal Rankine and Carnot power cycle: ·①Instead of isentropic compression from3→4(Carnot),itis isentropic pumping from saturated liquid (3)to subcooled liquid (4)(Rankine)due to the use of actual working fluid (water/steam) ·②Quality at turbine exit not too low> Cooling curve for the products of combustion 3Rankine:Non-isothermal heat addition,good the combustion heat ·④Carnot:two-phase pump is hard to handle 上游通大学 May4,2018 9 SHANGHAI JIAO TONG UNIVERSITY
May 4, 2018 9 Continue Ideal Rankine Power Cycle Define ideal Rankine power cycle: • Neglect the finite temperature difference of heat exchanger ∆THX = 0, TBoiler = TH and TCond = TL • Isentropic expansion and pumping processes s1=s2 and s3=s4 Difference between ideal Rankine and Carnot power cycle: • ① Instead of isentropic compression from 3 4 (Carnot), it is isentropic pumping from saturated liquid (3) to subcooled liquid (4) (Rankine) due to the use of actual working fluid (water/ steam) • ② Quality at turbine exit not too low • ③ Rankine: Non-isothermal heat addition, good for using the combustion heat • ④ Carnot: two-phase pump is hard to handle
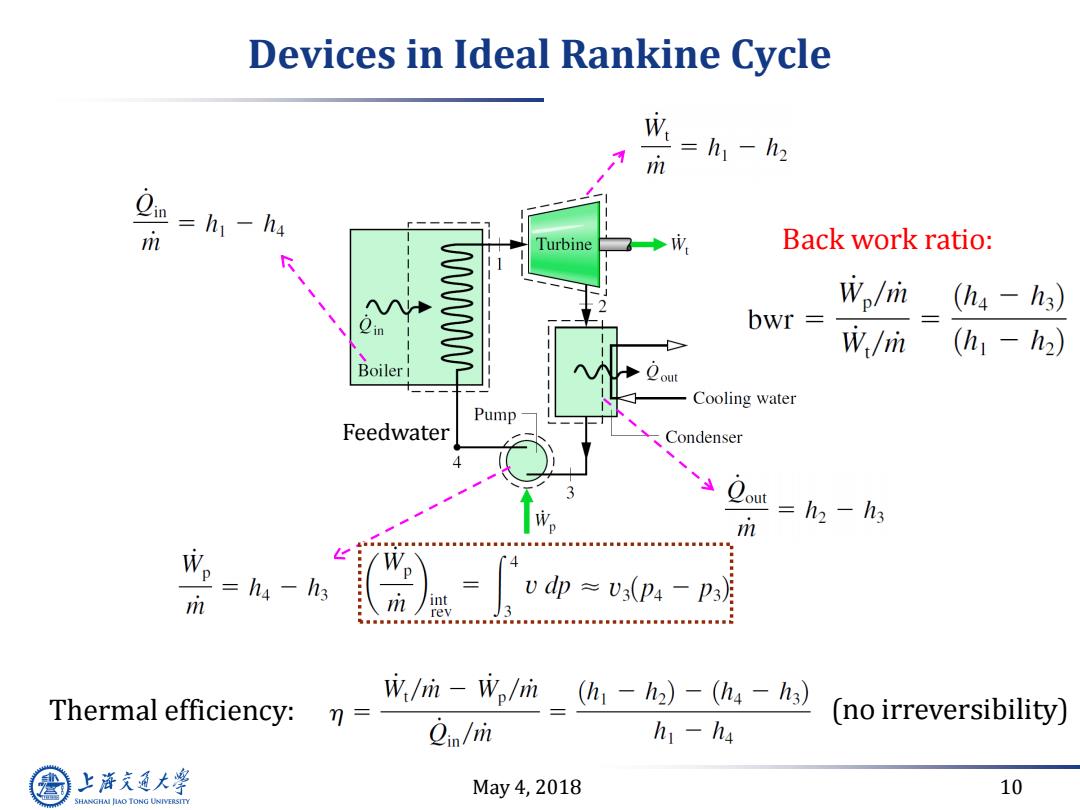
Devices in Ideal Rankine Cycle W=h一h m m =h-h4 Turbine Back work ratio: VWWWWWWM Wo/m (hs-h3) bwr 成/m (h1-h2) Boiler 1 Cooling water Pump Feedwater Condenser m =h2 -h3 m /int Vdp≈V3(P4-p3月 rev Thermal efficiency: W/m-W./m(h1-h2)-(h4-hs) 7= (no irreversibility) 2in/m h1-h4 上游充通大 May4,2018 10 SHANGHAI JIAO TONG UNIVERSITY
May 4, 2018 10 Devices in Ideal Rankine Cycle Feedwater Thermal efficiency: Back work ratio: (no irreversibility)