
第五讲立体的投影 第一节 基本体的投影 第二节 平面与立体相交 第三节 立体与立体相交 01 合U
第五讲 立体的投影 第一节 基本体的投影 第二节 平面与立体相交 第三节 立体与立体相交 01

第一节基本体的投影 表面仅由平面围成的基本 机件都可以看作 体:平面立体 由一些基本几何体 组合而成, ·最基本的简单立 环 球 四棱锥 体称为基本体。如: 棱柱、棱锥、圆柱、 圆柱 圆锥、球、环等。 它们是构成形体的 基本单元。 圆锥 o 基本体分为平面 表面包含曲面的基本体: 立体和曲面立体 曲面立体 六棱柱 02 囧U☒
表面仅由平面围成的基本 体 : 平面立体 表面包含曲面的基本体: 曲面立体 • 机件都可以看作 由一些基本几何体 组合而成, • 最基本的简单立 体称为基本体。如: 棱柱、棱锥、圆柱、 圆锥、球、环等。 它们是构成形体的 基本单元。 • 基本体分为平面 立体和曲面立体 球 圆 环 四棱锥 圆柱 圆锥 六棱柱 第一节 基本体的投影 02

第一节基本体的投影 平面立体 (一)棱柱 1、投影分析 (正六棱柱) a d"e 顶面和底面均为水平面,它们 的水平投影反映实形,正面和侧 面投影重影为一直线。 ·前后棱面为正平面,它们的正 b 面投影反映实形,水平和侧面投 影重影为一直线。 ·其他四个棱面为铅垂面,其水 平投影均重影为直线,正面和侧 a 面投影均为类似形 棱线AB为铅垂线,水平投影ab重影为一点,正面和侧 面投影均反映实形。顶面的边DE为侧垂线,侧面投影 d”e”重影为一点,水平和正面投影均反映实形。底面的 边BC为水平线,水平投影反映实长,正面投影外'c和侧 面投影%”c”均小于实长。 作图时,先画正六棱柱的水平投影正六边形,再根据投 影规律作出其他两个投影。 合心K
第一节 基本体的投影 一、 平面立体 (一) 棱柱 1、投影分析(正六棱柱) • 顶面和底面均为水平面,它们 的水平投影反映实形,正面和侧 面投影重影为一直线。 • 前后棱面为正平面,它们的正 面投影反映实形,水平和侧面投 影重影为一直线。 • 其他四个棱面为铅垂面,其水 平投影均重影为直线,正面和侧 面投影均为类似形 棱线AB为铅垂线,水平投影ab重影为一点,正面和侧 面投影均反映实形。顶面的边DE为侧垂线,侧面投影 d”e”重影为一点,水平和正面投影均反映实形。底面的 边BC为水平线,水平投影反映实长,正面投影b’c’和侧 面投影b”c”均小于实长。 作图时,先画正六棱柱的水平投影正六边形,再根据投 影规律作出其他两个投影。 03
第一节基本体的投影 一、平面立体 一)棱柱 a a" 2、棱柱表面取点 例:已知棱柱表面M点的正面 b 投影m'和N点的侧面投影n”, 求出其他两面投影。 a 利用特殊位置表面的积聚性取点 ·由于m'是可见的,因此M点必定在ABCD 棱面上,而ABCD棱面为铅垂面,水平投影 abcd有重影性,因而m必定在abcd上。再根据 m和m即可求出m”。 。 同理作n和n,且n不可见。 合K
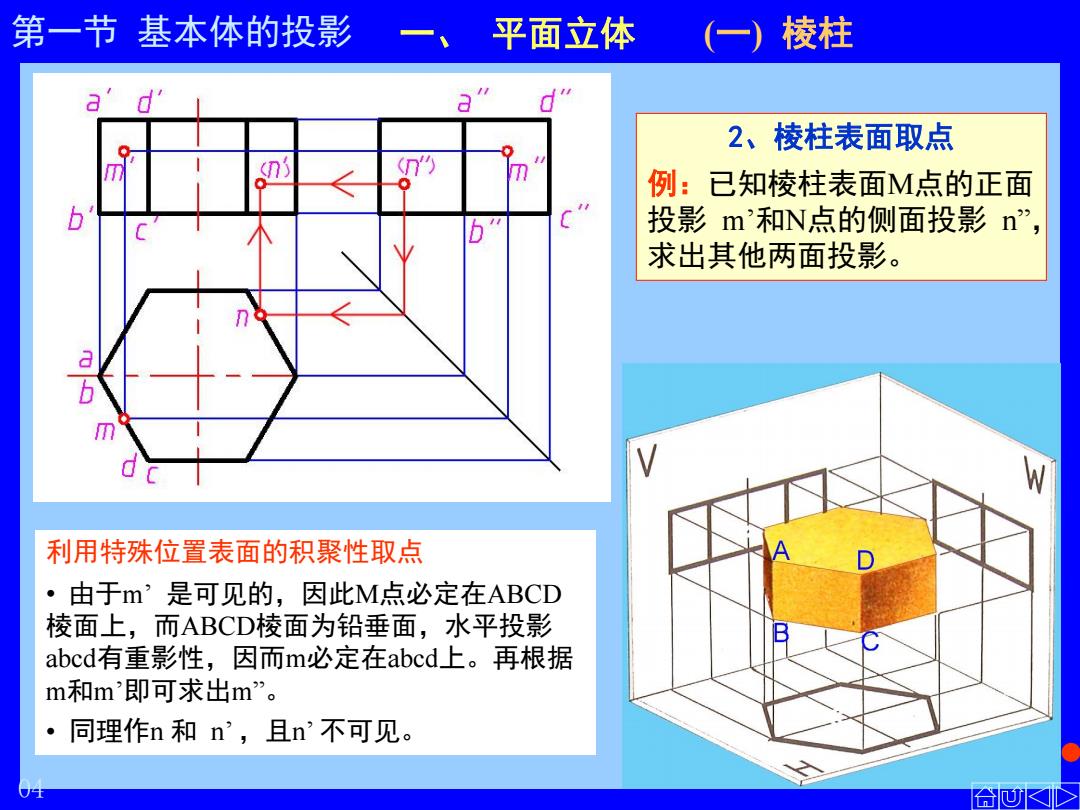
第一节 基本体的投影 一、 平面立体 (一) 棱柱 2、棱柱表面取点 例:已知棱柱表面M点的正面 投影 m’和N点的侧面投影 n” , 求出其他两面投影。 利用特殊位置表面的积聚性取点 • 由于m’ 是可见的,因此M点必定在ABCD 棱面上,而ABCD棱面为铅垂面,水平投影 abcd有重影性,因而m必定在abcd上。再根据 m和m’即可求出m”。 • 同理作n 和 n’ ,且n’ 不可见。 04
第一节基本体的投影 、平面立体 (二)棱锥 1、投影分析(正三棱锥) ·锥推顶为S,其底面为正△ABC,呈 水平位置,水平投影△abc反映实形。 ·棱面△SAB、△SBC是倾斜面,各 投影均是类似形 a b' a b” ·棱面△SAC为侧垂面,其侧面投影 重影为一直线 a 作图时,先画底面正△ABC的各个投 影,再作出锥顶$的各个投影,然后连 接各棱线 合K
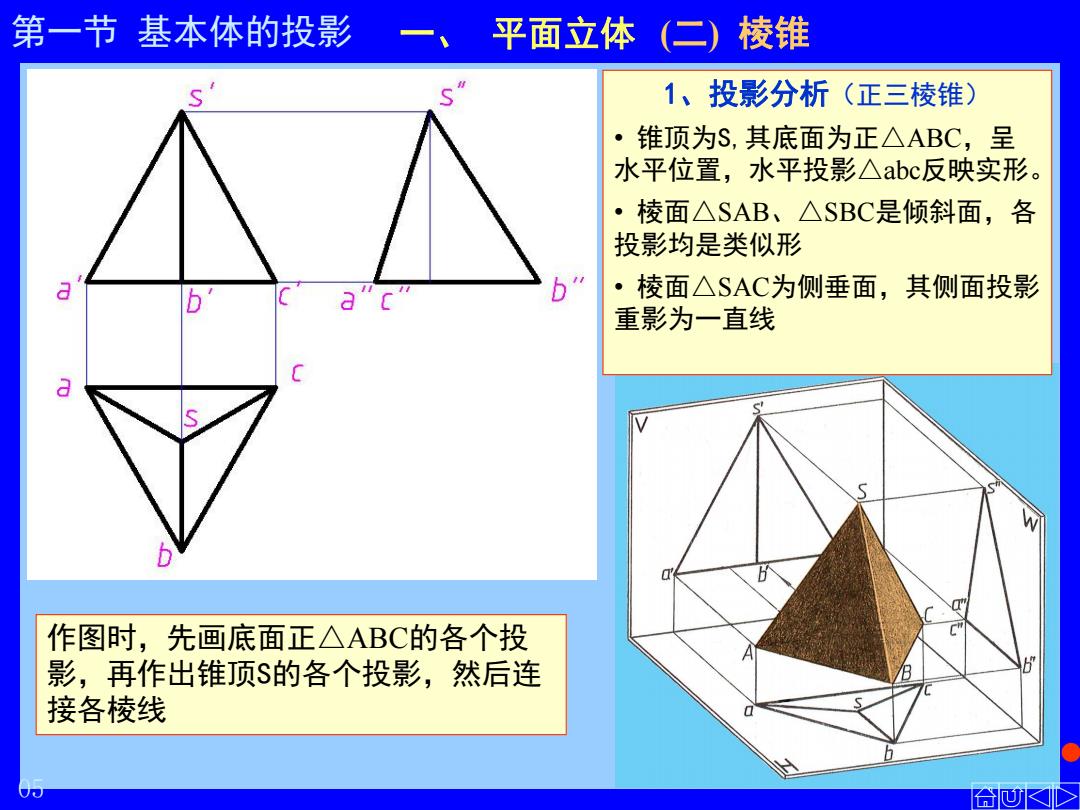
第一节 基本体的投影 一、 平面立体 (二) 棱锥 作图时,先画底面正△ABC的各个投 影,再作出锥顶S的各个投影,然后连 接各棱线 1、投影分析(正三棱锥) • 锥顶为S,其底面为正△ABC,呈 水平位置,水平投影△abc反映实形。 • 棱面△SAB、△SBC是倾斜面,各 投影均是类似形 • 棱面△SAC为侧垂面,其侧面投影 重影为一直线 05
第一节基本体的投影 一、平面立体 (二)棱锥 2、棱锥表面取点 【例1】已知M点的正面投影m?, 求其他两投影 方法一M点在棱面SAB上。过M在 △ABC上作AB的辅助平行线IM, 即作1'm'∥ab',再作1m∥ab,求 出m',再根据m、m求出m” a b 方法二过锥顶S和M点作辅助线SIⅡ,然后再 求M点的水平投影m 合K
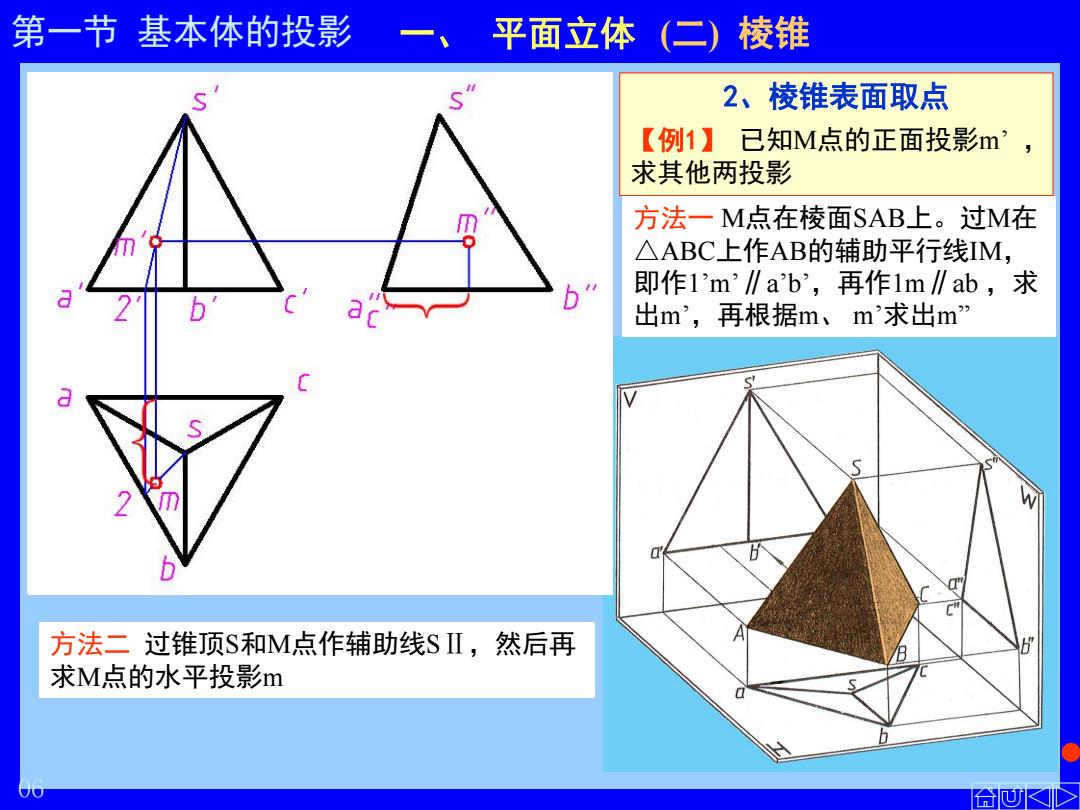
第一节 基本体的投影 一、 平面立体 (二) 棱锥 2、棱锥表面取点 【例1】 已知M点的正面投影m’ , 求其他两投影 方法二 过锥顶S和M点作辅助线SⅡ,然后再 求M点的水平投影m 方法一 M点在棱面SAB上。过M在 △ABC上作AB的辅助平行线ІM, 即作1’m’∥a’b’ ,再作1m∥ab ,求 出m’ ,再根据m、 m’求出m” 06
第一节基本体的投影 一、平面立体 (二)棱锥 (n) 2、棱锥表面取点 【例2】已知N点的水平投影n, 求其他两投影 a δY δY N点在侧垂面SAC上,因此n”必定在s”a”c, 由n、n可求出n',n为不可见。 合K
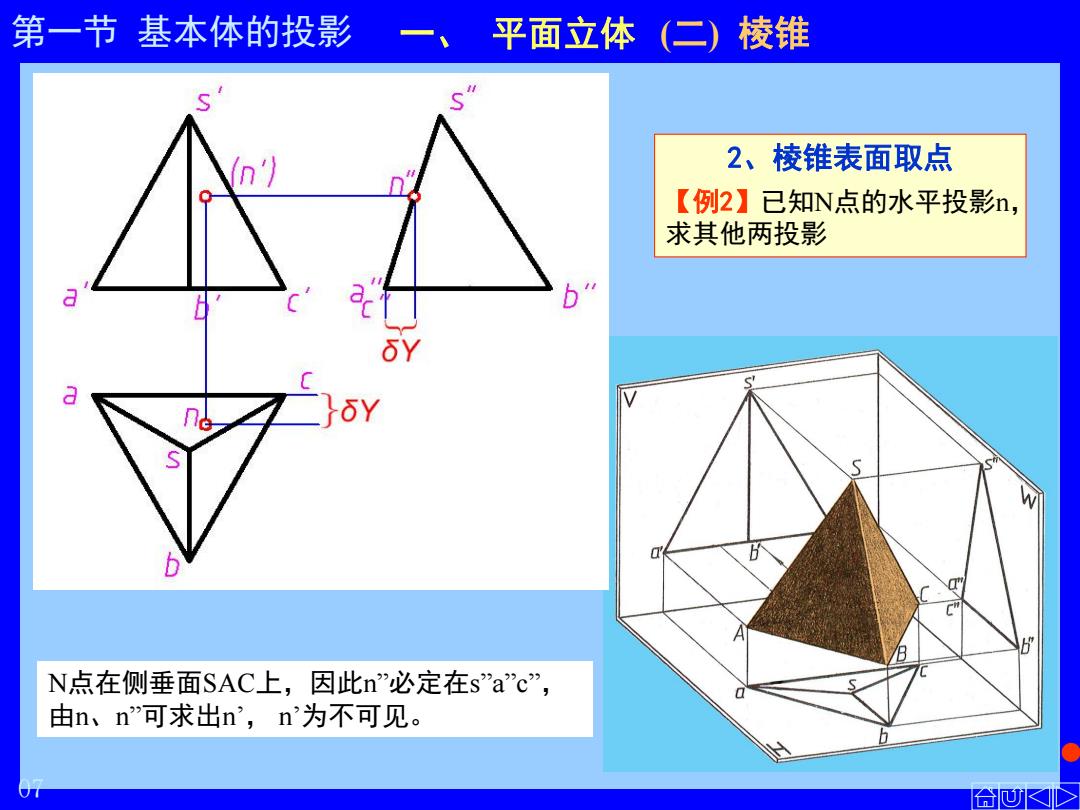
第一节 基本体的投影 一、 平面立体 (二) 棱锥 2、棱锥表面取点 【例2】已知N点的水平投影n, 求其他两投影 N点在侧垂面SAC上,因此n”必定在s”a”c” , 由n、n”可求出n’ , n’为不可见。 07
第一节基本体的投影二、【 曲面立体 (一)圆柱 1、圆柱的投影 ·工程中常见的曲面立体是回转体,如圆柱、 圆锥、球体、圆环。 ·圆柱表面由圆柱面和项、底圆所组成。 ·圆柱面是一直母线绕与之平行的轴线回转而 成,曲面上任一位置的母线称为素线。 ·顶圆、底圆为水平面,其H面投影反映实形, V面、W面投影积聚为直线。 注意:画曲面立体投影 图时,轴线要用细点画 对正面的 线画出,圆的中心线用 转向轮廓线 相互垂直的细点画线画 出,其交点为圆心。画 细点画线时,应超出轮 廓线2-5mm。 圆柱面的H面投影积聚为一圆,V面和W面投影各为 一矩形。 ·V面投影中矩形两边的垂直线是圆柱面上最左、最右 两条素线的投影,是圆柱面前后两部分的分界线,所 以称为对正面的转向轮廓线 对侧面的 ·W面投影中矩形两边的垂直线是对侧面的转向轮廓线 转向轮廓线 合心K
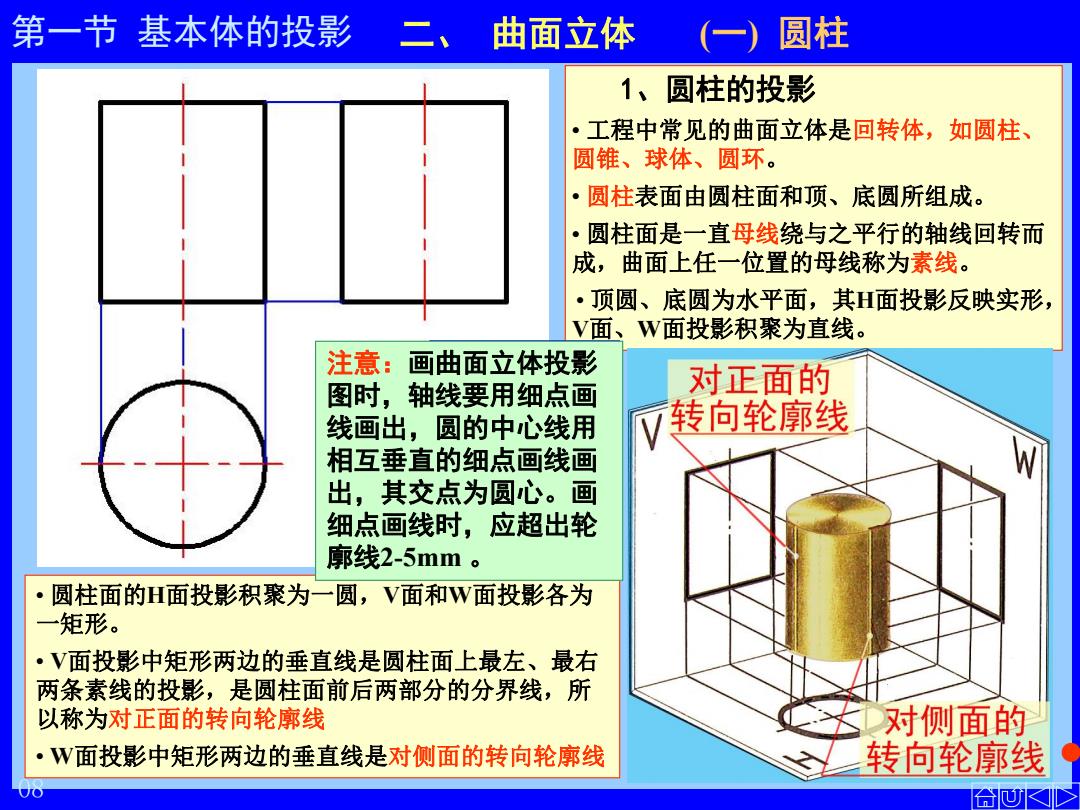
第一节 基本体的投影 二、 曲面立体 (一) 圆柱 1、圆柱的投影 • 工程中常见的曲面立体是回转体,如圆柱、 圆锥、球体、圆环。 • 圆柱表面由圆柱面和顶、底圆所组成。 • 圆柱面是一直母线绕与之平行的轴线回转而 成,曲面上任一位置的母线称为素线。 • 顶圆、底圆为水平面,其H面投影反映实形, V面、W面投影积聚为直线。 • 圆柱面的H面投影积聚为一圆,V面和W面投影各为 一矩形。 • V面投影中矩形两边的垂直线是圆柱面上最左、最右 两条素线的投影,是圆柱面前后两部分的分界线,所 以称为对正面的转向轮廓线 • W面投影中矩形两边的垂直线是对侧面的转向轮廓线 注意:画曲面立体投影 图时,轴线要用细点画 线画出,圆的中心线用 相互垂直的细点画线画 出,其交点为圆心。画 细点画线时,应超出轮 廓线2-5mm 。 08
第一节基本体的投影二、【 曲面立体 (一)圆柱 2、圆柱表面上取点 【例】已知圆柱面上M点的正面投影 m',和N点的侧面投影n”求其他两面的 (m)! 投影。 ·利用圆柱面的H面投影的积聚性,可 以直接得到水平投影m ·由于m'是不可见的,因此M点必定在 后半个圆柱面上,水平投影m必定落在 具有重影性的后半水平投影圆上 。再由m和m'求出m” ·不可见,N点必定在右半圆柱面,水平投 影n必定在具有右半水平投影圆上 。再由n和n求出n 合K
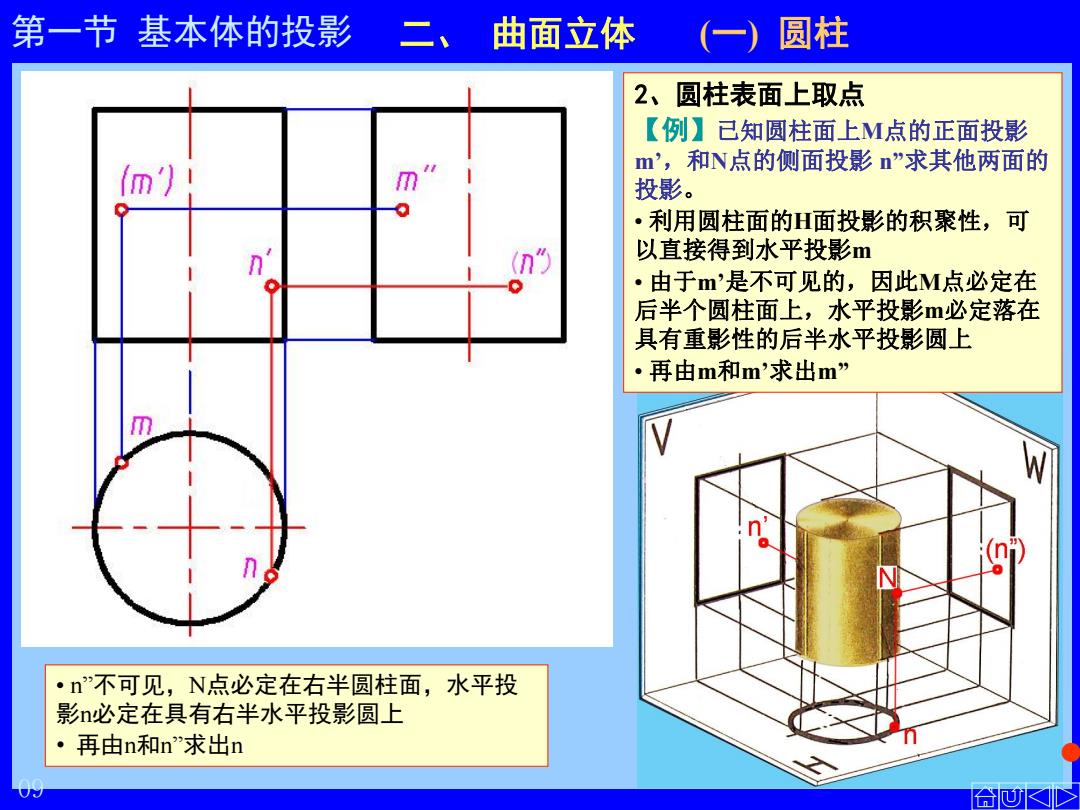
第一节 基本体的投影 二、 曲面立体 (一) 圆柱 • n”不可见,N点必定在右半圆柱面,水平投 影n必定在具有右半水平投影圆上 • 再由n和n”求出n 2、圆柱表面上取点 【例】已知圆柱面上M点的正面投影 m’ ,和N点的侧面投影 n”求其他两面的 投影。 • 利用圆柱面的H面投影的积聚性,可 以直接得到水平投影m • 由于m’是不可见的,因此M点必定在 后半个圆柱面上,水平投影m必定落在 具有重影性的后半水平投影圆上 • 再由m和m’求出m” 09
第一节基本体的投影二、 曲面立体 (三)球 球的三面 投影都是 圆,它们 分别是球 上相应的 转向轮廓 线的投影 合心K
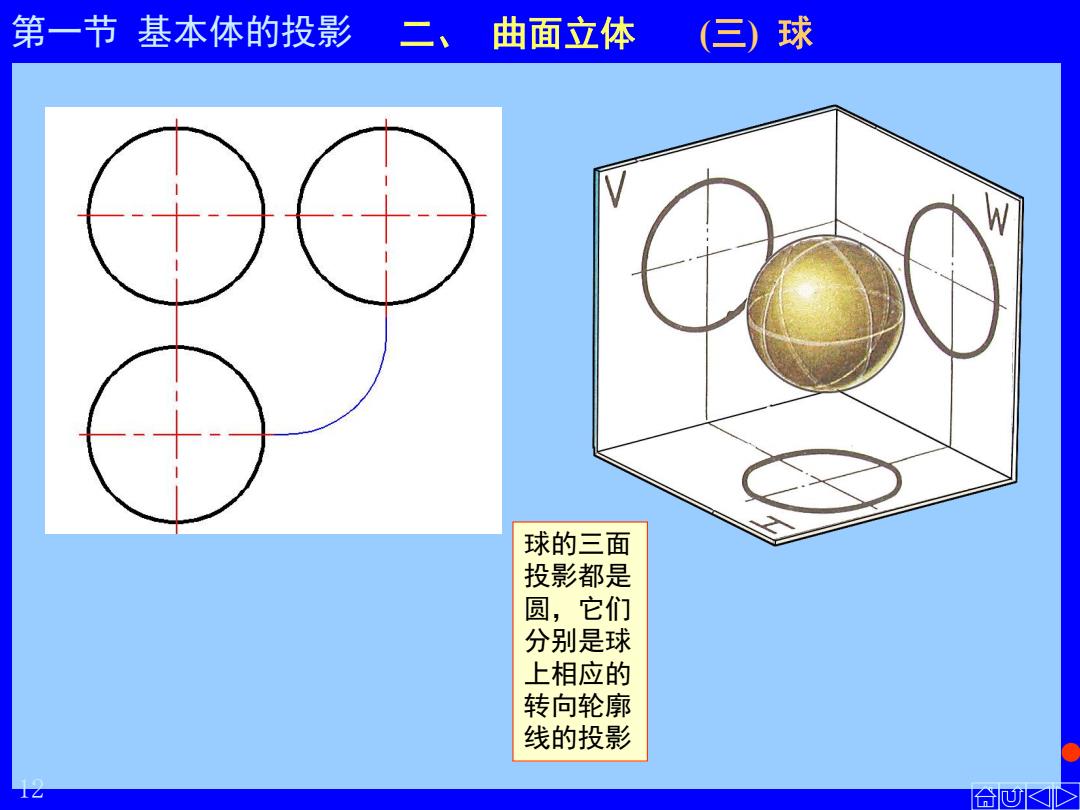
第一节 基本体的投影 二、 曲面立体 (三) 球 球的三面 投影都是 圆,它们 分别是球 上相应的 转向轮廓 线的投影 12