
第3章平面机构的运动分析 (一)教学要求 1、能根据实物绘制机构运动简图 2、熟练掌握机构自由度计算方法。了解机构组成原理 了解平面机 运动分析的方法,掌握瞬心法对机构进行速度分析 4、熟练掌握相对运动图解法 (二)教学的重点与难点 1、机构及运动副的概念、绘机构运动简图 2、自由度计算,虚约束,高副低代 3、瞬心的概念及求法 4、矢量方程,速度和加速度多边形,哥氏加速度,影像法 (三)教学内容 §3-1研究机构运动分析的目的和方法 一、目的:在设计新的机械或分析现有机械的工作性能副, 都必须首先计算其机构的运动参数。 二、方法: 图解法:形象直观,精度不高,速度瞬心法,相对运动 图解 解析法:较高的精度,工作量大 实验法: §3-2速度瞬心法及其在机构速度分析上 的应用 一、速度瞬心:两构件上相对速度为零的重合点: 瞬时绝对速度相同的重合点。 相对速度瞬心:两构件都是运动的 绝对速度瞬心:两构件之一是静止的 ii年p (由理论力学可知,任一时刻,刚体1和2的相对运动可以看作是纯一重合点的转动, 设该重点点为P:(图示位置),现在确定1,2重合点A的相对运动方向,即相对速度方向, 称重合点P?为瞬时回转中心,或速度瞬心。 二、机构中瞬心的数目:
Y O X B1B2 12 v 1 P B vA1A2 A 1 2 第 3 章 平面机构的运动分析 (一)教学要求 1、能根据实物绘制机构运动简图 2、熟练掌握机构自由度计算方法。了解机构组成原理 3、了解平面机构运动分析的方法,掌握瞬心法对机构进行速度分析 4、熟练掌握相对运动图解法 (二)教学的重点与难点 1、机构及运动副的概念、绘机构运动简图 2、自由度计算,虚约束,高副低代 3、瞬心的概念及求法 4、矢量方程,速度和加速度多边形,哥氏加速度,影像法 (三)教学内容 §3-1 研究机构运动分析的目的和方法 一、目的:在设计新的机械或分析现有机械的工作性能副, 都必须首先计算其机构的运动参数。 二、方法: 图解法:形象直观,精度不高,速度瞬心法,相对运动 图解法 解析法:较高的精度,工作量大 实验法: §3-2 速度瞬心法及其在机构速度分析上 的应用 一、速度瞬心:两构件上相对速度为零的重合点: 瞬时绝对速度相同的重合点。 相对速度瞬心:两构件都是运动的 绝对速度瞬心:两构件之一是静止的 i,j → Pij (由理论力学可知,任一时刻,刚体 1 和 2 的相对运动可以看作是纯一重合点的转动, 设该重点点为 P12(图示位置),现在确定 1,2 重合点 A 的相对运动方向,即相对速度方向, 称重合点 P12 为瞬时回转中心,或速度瞬心。 二、机构中瞬心的数目:
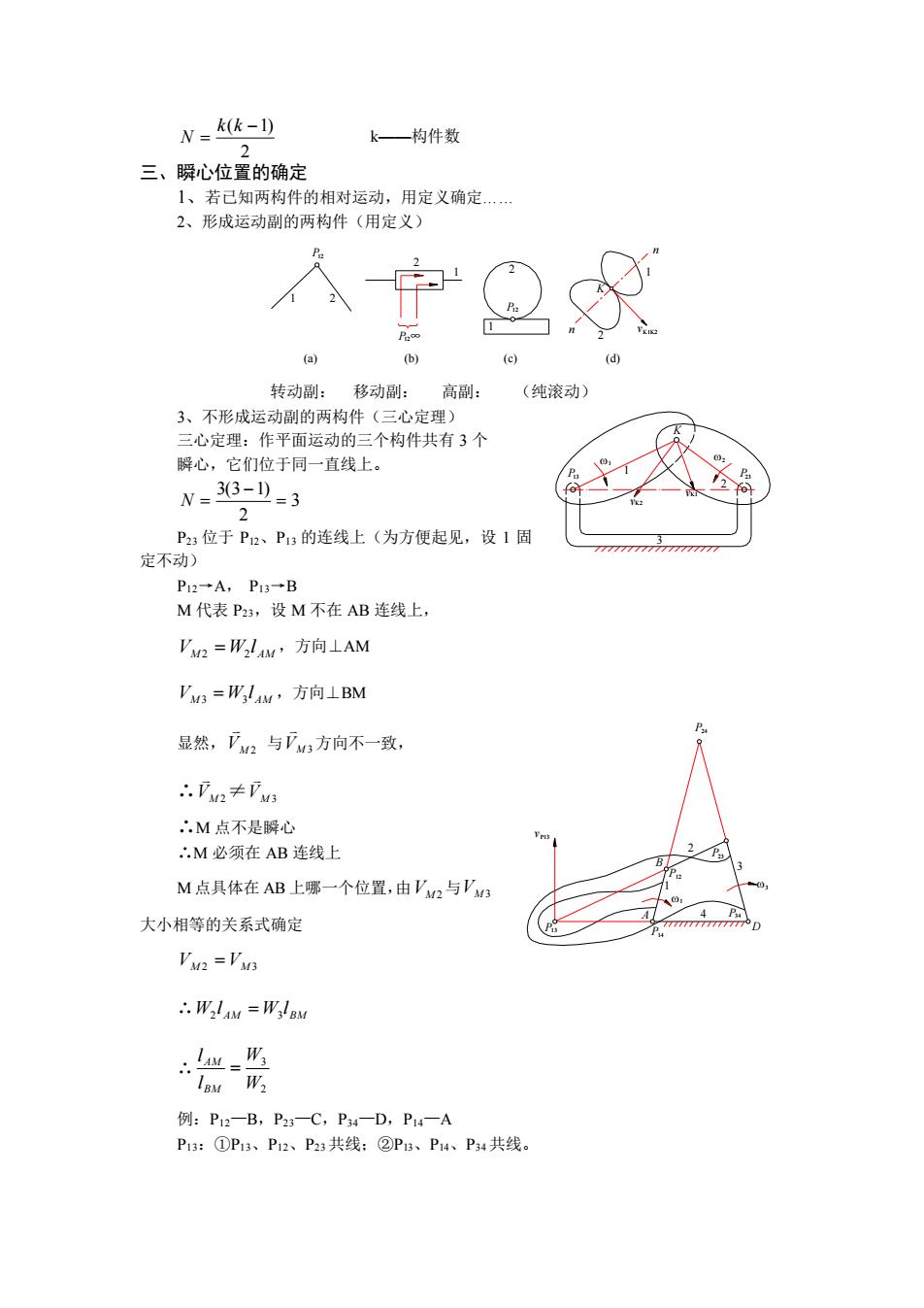
N=k(k-1) k—构件数 三、瞬心位置的确定 1、若已知两构件的相对运动,用定义确定. 2、形成运动副的两构件(用定义) b 转动剧:移动副:高副:(纯滚动) 瞬心,它们位于同一直线上。 N-33-3 P:位于P2、P:的连线上(为方便起见,设1固 定不动 P12+A,P13+B M代表P23,设M不在AB连线上, '2=WlAw'方向⊥AM VM=W,14M,方向⊥BM 显然,下2与方向不一致, ∴2≠刀 ∴M点不是瞬心 ,',M必须在AB连线上 M点具体在AB上哪一个位置,由'M2与'M 大小相等的关系式确定 'a='a Wilay W lew 例:P12一B,PC,P4一D,P14一A P13:①P1s、P12、P2共线:②P、P1、P共线
12 (a) (b) P12∞ 2 (c) 1 n (d) vK1K2 1 P 1 2 2 12 K 2 P 1 n 2 ( −1) = k k N k——构件数 三、瞬心位置的确定 1、若已知两构件的相对运动,用定义确定. 2、形成运动副的两构件(用定义) 转动副: 移动副: 高副: (纯滚动) 3、不形成运动副的两构件(三心定理) 三心定理:作平面运动的三个构件共有 3 个 瞬心,它们位于同一直线上。 3 2 3(3 1) = − N = P23 位于 P12、P13 的连线上(为方便起见,设 1 固 定不动) P12→A, P13→B M 代表 P23,设 M 不在 AB 连线上, M AM V W l 2 = 2 ,方向⊥AM M AM V W l 3 = 3 ,方向⊥BM 显然, VM 2 与 VM 3 方向不一致, ∴ VM 2 ≠ VM 3 ∴M 点不是瞬心 ∴M 必须在 AB 连线上 M 点具体在 AB 上哪一个位置,由 VM 2 与 VM 3 大小相等的关系式确定 VM 2 = VM 3 ∴ AM BM W l W l 2 = 3 ∴ 2 3 W W l l BM AM = 例:P12—B,P23—C,P34—D,P14—A P13:①P13、P12、P23 共线;②P13、P14、P34 共线。 vK1 vK2 3 P13 1 1 P23 2 2 K 2 P 1 P13 A P14 B P34 1 4 D P12 23 3 3 v P13 P24

N=4×4-0=6 :用时对礼行动分 P1、P:共线:②P、Ps、P3共线 例:图示机构中,已知14B,1ac,p,构件2,以o2逆时针方向转动。 求:①机构的全部瞬心位置:②从动件4 的速度。 解:、画机构运动简图,取以。=amm mml B(P 2、求瞬心 N-4x4-D=6 P12一A,P3一B,P4C,P14一⊥无空道 处 P13:①P13、P12、P2:共线:②P1、P14、P共线 P24:①P24、P12、P14共线:②P24、P23、P4共线 3、从动件4的速度 'a='w4='4 Vu =WalavMr 例:凸轮以匀速逆时针转动,求该位置时 从动件2的速度V,。 解:1、取4,作机构运动简图 2、求瞬心, 共线:①P13→A:②P2一⊥CD无究 道处:③P2→接触点公法线上 注意:①V:②构件数图较少时用。 P12-0,V2=Vo2 =Val =Wlo'Hc 作业:P505:2-1,2-2,2-3 §3一3用矢量方程图解法求机构的速度和加速度 相对运动图解法:用相对运动原理列出构件上点与点之间的相对运动矢量方程,然后作 图求解矢量方程。 速度,加速度(用基点法求刚体的运动度) 复习:相对运动原理。 1)刚体(构件)的平面运动分解为随基点的平动加上绕基点的转动。 了=V+a dg=a+aB 2)点的速度合成定理:(动点在某解时的绝对速度等于它在该解时的牵连速度与相对 速度的矢量和)
6 2 4 (4 1) = − N = P24:①P24、P12、P14 共线;②P24、P23、P34 共线。 四、利用瞬时对机构进行运动分析 例:图示机构中,已知 AB l , BC l , ,构件 2,以 2 逆时针方向转动。 求:①机构的全部瞬心位置;②从动件 4 的速度。 解:1、画机构运动简图,取 mm1 mm c = a 2、求瞬心 6 2 4 (4 1) = − N = P12→A,P23→B,P34→C,P14→⊥无空道 处 P13:①P13、P12、P23 共线;②P13、P14、P34 共线 P24:①P24、P12、P14 共线;②P24、P23、P34 共线 3、从动件 4 的速度 VM 2 =VM 4 =V4 M AM l V 2 = W2 l 例:凸轮以匀速逆时针转动,求该位置时 从动件 2 的速度 V2 。 解:1、取 l 作机构运动简图 2、求瞬心, 共线:①P13→A;②P23→⊥CD 无究 道处;③P12→接触点公法线上 注意:①V;②构件数图较少时用。 P12→O, o o AO C V2 =V 2 =V 1 = W1 l 作业:P505: 2—1,2—2,2—3 §3—3 用矢量方程图解法求机构的速度和加速度 相对运动图解法:用相对运动原理列出构件上点与点之间的相对运动矢量方程,然后作 图求解矢量方程。 速度,加速度(用基点法求刚体的运动度) 复习:相对运动原理。 1)刚体(构件)的平面运动分解为随基点的平动加上绕基点的转动。 VB =VA +VBA aB = aA + aBA 2)点的速度合成定理:(动点在某瞬时的绝对速度等于它在该瞬时的牵连速度与相对 速度的矢量和) B(P ) 4 A 1 14 (P ) 12 1 2 3 C(P ) 23 P P 34 13 n (P ) A 1 21 3 2 B 31 (P ) n P32 3 C 3

(重合点法) 绝对运动 牵连运动 相对运动 动点对静系的运动 动系对静系的运动 动点对动系 点的运动 刚体运动 点的运动 可-可+可 动系平动:a=a+0=r+ 动系转动:a。=a。+a+a 一、在同一构件上点间的速度和加速度的求法(基点法) 01 pb mm 己知机构各构件的长度,0,a 求:02a2,ac,a,0,a1 解:1→定轴转动:2一平面一般运动(平动,转动),3一定轴转动。 取4c作机构运动简图。 1、求速度和角速度 区=可+ 方向⊥CD⊥AB⊥BC Ve=4,·pe,Vs=4,b 了E=可+E=E+c 方向?pb⊥BEpC⊥EC
(重合点法) 绝对运动 = 牵连运动 + 相对运动 动点对静系的运动 动系对静系的运动 动点对动系 点的运动 刚体运动 点的运动 Va = Ve +Vr 动系平动: aa = ae + ar Va = Ve +Vr 动系转动: aa = ae + ar + ak 一、在同一构件上点间的速度和加速度的求法(基点法) mm mls pb l V AB v = 1 已知机构各构件的长度, 1 1 , 求: 2 2 3 3 , ,VC ,VE ,aC ,aE , , 。 解:1→定轴转动;2→平面一般运动(平动,转动),3→定轴转动。 取 C 作机构运动简图。 1、求速度和角速度 VC = VB +VCB 方向⊥CD ⊥AB ⊥BC 大小 ? AB l 1 ? V pc C v = , V bc CB v = VE =VB +VEB =VC +VEC 方向 ? pb ⊥BE pc ⊥EC A 4 B 1 1 D c 2 E 1 3 2 2 3 e 3 C b p

大小?ela?4心? p呢→万 i.Vs=pe 会方: 上=,严,逆时针 Icp 在速度多边形中, △bce和△BCE相似 图形bce为BCE的速度影响像 速度影像的用处: 在速度多边形中:P一极点,bc→Vc 注意:速度影像只能应用于同一构件上的各点。 2、求加速度,角加速度 dc =as+dca 或a+d.=a6+dg+an+ad 方向C-D⊥CDB-A⊥ABC一B⊥BC 大小o1m?o1指alB lec? nC→a,大小ac=4。C。C"C→ad,ad=4nC"C 求ae:aE=aB+aEn+ai 方向?T一b'E一B⊥BE 大小?4。币lEa,lae 0→aE,a=4, 加速度多边形中 acn =(aca)+(acn)=lon)+(azlcn)=lca +ai 同理:am=lnVo+aGac=lcV回+a吲
大小 ? AB l 1 ? pc k ? pe →VE ∴ V pe E k = BC CB l V 2 = , 方向:顺时针, CD V CD C l pc l V 3 = = ,逆时针 在速度多边形中, △bce 和 △BCE 相似 图形 bce 为 BC’E 的速度影响像。 速度影像的用处: 在速度多边形中:P→极点, bc →V CB 注意:速度影像只能应用于同一构件上的各点。 mm m s b a n B a / = 2、求加速度,角加速度 aC = aB + aCB 或 CB n CB t B n B t c n ac + a = a + a + a + a 方向 C→D ⊥CD B→A ⊥AB C→B ⊥BC 大小 CD l 2 3 ? AB l 2 1 AB l 1 BC l 2 2 ? C → aC ,大小 aC = a C。CC → aCB aCB = aCC , ∵ CB BC a l 2 = ∴ BC CB l a 2 = CD a CD C l C C l a = = 3 求 E a : EB n aE = aB + aEB + a 方向 ? π→b′ E→B ⊥BE 大小 ? a b BE l 2 2 BE l 2 aE e → , a e E a = 加速度多边形中: 2 2 4 2 2 2 2 2 2 2 2 ( ) ( ) ( ) ( ) = + CB = CB + CB = CB + n CB CB a a a l l l 同理: 2 2 4 aEB = lEB 2 + 2 2 4 aEC = lEC 2 +

ac:am:arc=lc:l:l ub':H,Be:uce=u BC:uEB:H.EC :b'c':b'e':c'e'=BC:EB:EC .b'c'e和BCE相似 称bc'e'为BCE的加速度影像。 用处 注意:只用于机构中同一构件上各点。 r为极点。 作业:P:2-4,2.5 二、组成移动副两构件的重合点间的速度和加速度的求法(重合点法) (b 已知机构位置,尺寸,@,等角速 求,a3 解:1、取4作机构运动简图 2、求角速度 Vm =Vaz+Vam? 方向⊥BC⊥AB∥BC 大小?0l? pb,→Vg且V=4pb
∴ CB EB EC CB EB EC a : a : a = l : l : l a b c : a b e : a c e = l BC : c EB: c EC ∴ b c : b e : c e = BC : EB: EC ∴ b c e 和 BCE 相似 ∴ 称 b c e 为 BCE 的加速度影像。 用处: 注意:只用于机构中同一构件上各点。 π为极点。 作业:P506:2-4,2-5 二、组成移动副两构件的重合点间的速度和加速度的求法(重合点法) mm mls P V b B V 2 2 = mm mls b ac a 2 2 = 已知机构位置,尺寸, 1 等角速 求 3 3 , 。 解:1、取 c 作机构运动简图 2、求角速度 VB3 =VB2 +VB3B2 方向 ⊥BC ⊥AB ∥BC 大小 ? AB l 1 ? pb3 VB3 VB3 k pb3 → 且 = (a) (b) (c) 4 C 3 B A p b3 b'3 1 1 2 b (b ) 1 2 b''3 (b' ) b'1 2 k'
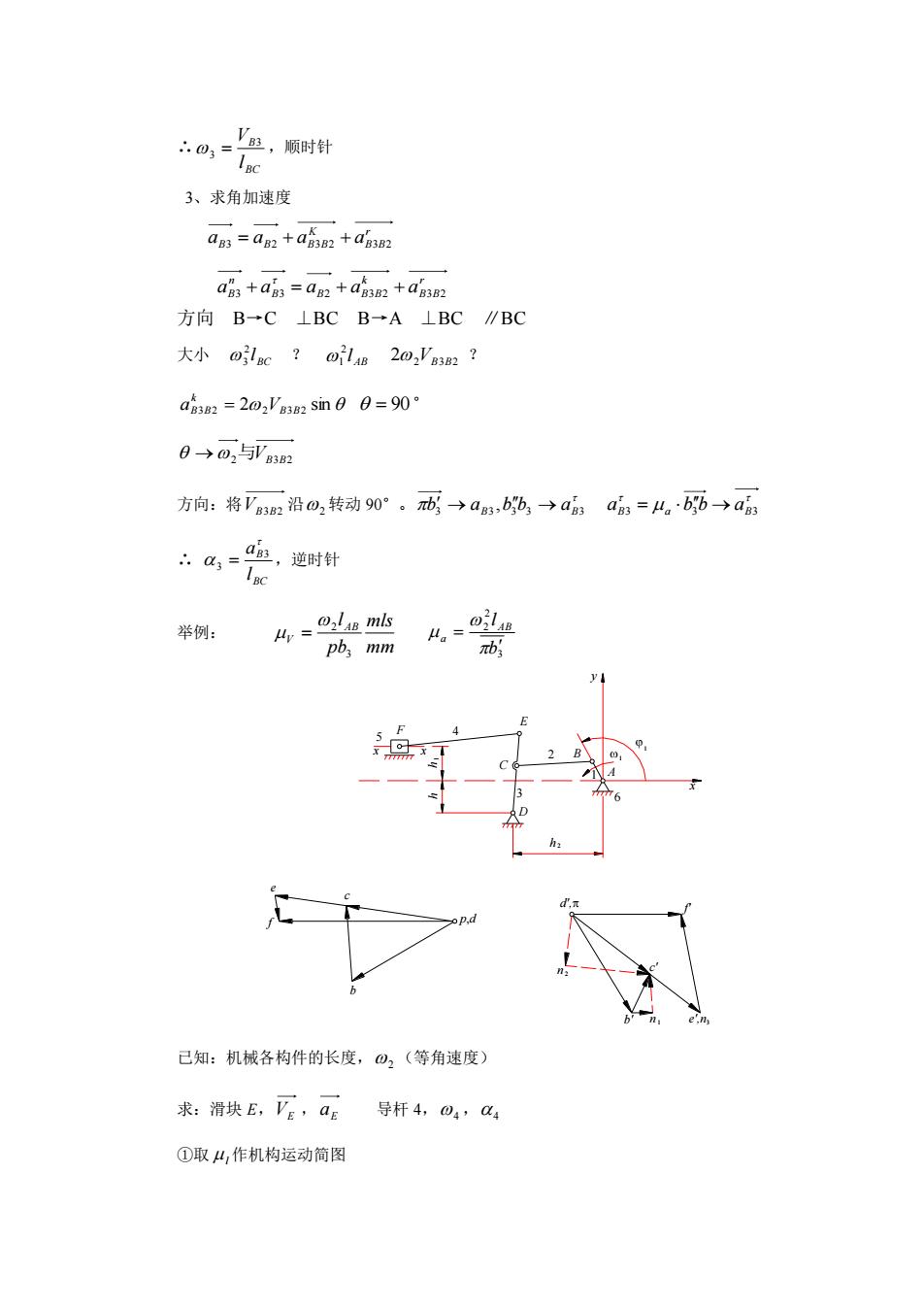
∴a,=鱼,顺时针 3、求角加速度 a=a+a喻a+am am +ain an +amm +amm 方向B→C⊥BCB-A⊥BC∥BC 大小oc?o1B20,'a32? ag82=20,'g32sin0日=90° 日→0,与32 方向:将沿@,转动90.西→ab%,→aa=4→a 举例:4,=,mb pb mm b 已知:机械各构件的长度,心2(等角速度) 求:滑块E,aE导杆4,04,a4 ①取4,作机构运动简图
x 5 y 1 C h D h2 3 h1 x F 4 E 2 B A 6 x 1 1 ∴ BC B l V 3 3 = ,顺时针 3、求角加速度 r B B K aB3 = aB2 + aB3B2 + a 3 2 r B B k B B B B n aB3 + a 3 = a 2 + a 3 2 + a 3 2 方向 B→C ⊥BC B→A ⊥BC ∥BC 大小 BC l 2 3 ? AB l 2 1 22VB3B2 ? 3 2 2 2 B3B2 sin k aB B = V = 90° →2与VB3B2 方向:将 VB3B2 沿 2 转动 90°。 3 3 3 3 3 , b aB b b → aB → aB3 a b3b → aB3 = ∴ BC B l a 3 3 = ,逆时针 举例: mm mls pb lAB V 3 2 = 3 2 2 b l AB a = 已知:机械各构件的长度, 2 (等角速度) 求:滑块 E,VE , E a 导杆 4,4 , 4 ①取 l 作机构运动简图 e f b c p,d d', n2 b' n (b) 1 e',n3 c' f

解:(1)VR=+VB4 方向上B,C上AB∥B,C大小?0,lB? pb→gVau=4:pb=o,lac 云0,=口方向:顺时针 构件5: (2)-s+ss 方向xx⊥CD⊥ED 大小?olm? pe,→Edse→'Esos 'E6='E5=4 pes Ves5as=4kde=05lD∴0,=口 (3)das=dm++ dis+dm=dm+dhm+dm 方向B4一C⊥B:CB-A⊥BC(上)∥B:C 大小oB4c?l4B20,'4B3? b6→ag∴a4=4,bb 小a会受.有老 (4)ag=ap+atp+asp 方向xxπ→d5ED⊥ED 大小?4,威on? →aEaE=4 作业:Ps062-7,2-8,2-10 §34用解析法求机构的位置、速度和加速度 复数矢量法:是将机构看成一封闭矢量多边形,并用复数形式表示该机构的封闭矢量方 程式,再将矢量方程式分别对所建立的直角坐标系取投影
解:(1) VB4 =VB3 +VB4B3 方向 ⊥B4C ⊥AB ∥B4C 大小 ? AB l 2 ? pb4 →VB4 ∴ VB4 = k B C pb l 4 =4 4 ∴ 4 = □ 方向:顺时针 构件 5: (2) VE5 =VD5 +VE5D5 方向 x-x ⊥CD ⊥ED 大小 ? CD l 4 ? ∴ pe5 →VE5 5 5 VE5D5 d e → VE6 VE5 k pe5 = = E d k ED V = d e = l 5 5 5 5 5 ∴ 5 = □ (3) r B B k aB4 = aB3 + aB4B3 + a 4 3 ∴ r B B k B B B B n aB4 + a 4 = a 3 + a 4 3 + a 4 3 方向 B4→C ⊥B4C B→A ⊥B4C(上) ∥B4C 大小 B C l 4 2 4 ? AB l 2 2 24VB4B3 ? b4b4 → aB4 ∴ aB = a bb 4 4 ∴ = = = B C a B C B l b b l a 4 4 4 4 4 4 √ 方向:逆时针 (4) ED n aE = aD + aED + a 方向 x-x d5 → E→D ⊥ED 大小 ? a d5 ED l 2 5 ? e a a e E E a → = 作业:P506 2-7,2-8,2-10 §3-4 用解析法求机构的位置、速度和加速度 复数矢量法:是将机构看成一封闭矢量多边形,并用复数形式表示该机构的封闭矢量方 程式,再将矢量方程式分别对所建立的直角坐标系取投影

先复习:矢量的复数表示法: a=ae=a(cosp+isin p)=a,+iay 己知各杆长分别为山4l4,0 求:p2,p3,02,03,62,5 解:1、位置分析,建立坐标系。, 封闭矢量方程式: 1+72=7+1 以复数形式表示:l,e+1,e9=l+l,e (a) 欧拉展开:(ep=cosp+isin) 1 (coso +isin )+(cos +isin )=+(cos +isin 实+i虚=实+i虚 求出:p2=f(p,) :=f(o) 2、速度分析:将式(a)对时间求导 Io ie+0ie=1@ie"(b) 消去,两边乘em hielee-s) 虚部 =hie) 按欧拉公式展开,取实部相等 %8 同理求a,=-8,15s9,-9) 1,sm0,-03) 角速度为正表示逆时针方向,角速度为负表示顺时针方向。 3、加速度分析 对(b)对时间求导 解析法在曲柄滑块机构和导杆机构中的应用,自学
先复习:矢量的复数表示法: x y i a = ae = a(cos + isin ) = a + ia 已知各杆长分别为 1 2 3 4 1 1 l l l l , , 求: 2 3 2 3 2 3 , , , , , 解:1、位置分析,建立坐标系。 1 2 3 4 l ,l ,l ,l , 封闭矢量方程式: 1 2 4 3 l l l l + = + 以复数形式表示: 1 2 3 1 2 4 3 i i i l e + l e = l + l e (a) 欧拉展开: ( cos sin ) e i i = + (cos sin ) (cos sin ) (cos sin ) 1 1 1 2 2 2 4 3 3 3 l + i + l + i = l + l + i 实+i 虚=实+i 虚 求出: ( ) ( ) 2 1 3 1 = f = f 2、速度分析:将式(a)对时间求导 1 2 3 1 1 2 2 3 3 i i i l ie + l ie = l ie (b) 消去 2 ,两边乘 2 i e − ( ) 3 3 ( ) ( ) 2 2 1 1 3 2 2 2 1 2 − − − + = i i i l ie l ie l ie 虚部 按欧拉公式展开,取实部相等 sin( ) sin( ) 3 3 2 1 1 2 3 1 − − = l l 同理求 sin( ) sin( ) 2 2 3 1 1 3 2 1 − − = − l l 角速度为正表示逆时针方向,角速度为负表示顺时针方向。 3、加速度分析: 对(b)对时间求导。 解析法在曲柄滑块机构和导杆机构中的应用,自学。 A y C' 1 1 4 D 3 x B 2 2 3 C