第二章平面机构的运动分析 一、填空题 1、速度瞬心是两刚体上 为零的重合点。 2、当两构件组成回转副时,其相对速度瞬心在 3、当两构件不直接组成运动副时,其瞬心位置用 确定 二、判断题(答A表示说法正确.答B表示说法不正确) 1、瞬心是两构件上瞬时相对速度为零的重合点。 2、利用瞬心既可以求机构的速度,又可以求加速度。 三、简答题 1、何谓速度瞬心?相对瞬心与绝对瞬心有何区别? 2、简述机构各瞬心位置的确定方法? 四、分析计算题 1、如图所示为一凸轮一连杆组合机构,设己知凸轮1的角加度,试用瞬心法确定在图示 位置时构件4较加速度4的大小和方向。 2、试判断在图所示两构件的B点是否都存在哥氏加速度?又在何位置时哥氏加速度为 零? 8
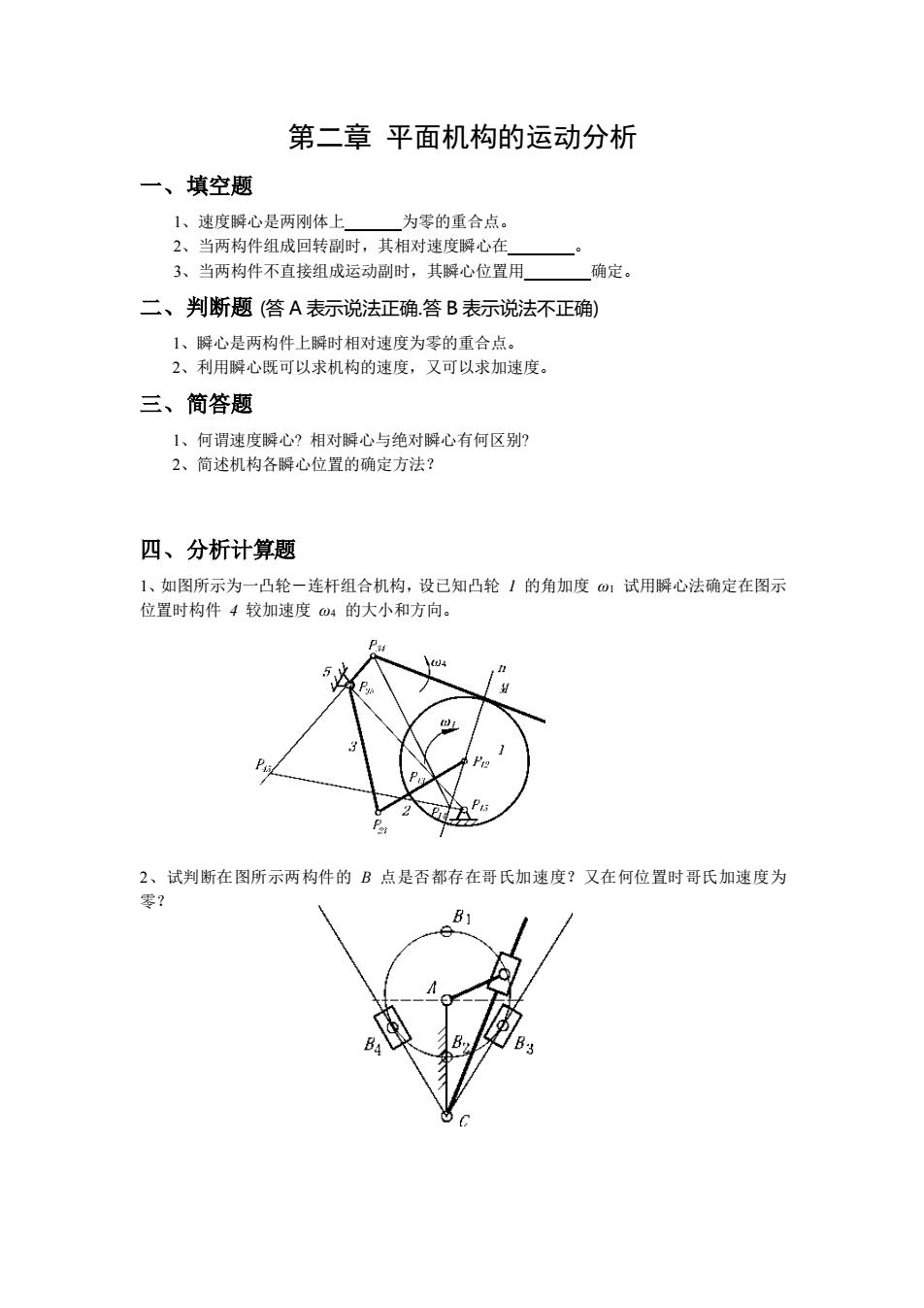
第二章 平面机构的运动分析 一、填空题 1、速度瞬心是两刚体上 为零的重合点。 2、当两构件组成回转副时,其相对速度瞬心在 。 3、当两构件不直接组成运动副时,其瞬心位置用 确定。 二、判断题 (答 A 表示说法正确.答 B 表示说法不正确) 1、瞬心是两构件上瞬时相对速度为零的重合点。 2、利用瞬心既可以求机构的速度,又可以求加速度。 三、简答题 1、何谓速度瞬心? 相对瞬心与绝对瞬心有何区别? 2、简述机构各瞬心位置的确定方法? 四、分析计算题 1、如图所示为一凸轮-连杆组合机构,设已知凸轮 1 的角加度 ω1 试用瞬心法确定在图示 位置时构件 4 较加速度 ω4 的大小和方向。 2、试判断在图所示两构件的 B 点是否都存在哥氏加速度?又在何位置时哥氏加速度为 零?

第二章平面机构的运动分析 习题解答 一、填空题 1、相对速度:2、三心定理来:3、两速度矢量的垂线的交点 二、判断题(答A表示说法正确答B表示说法不正确) 1、(B)片2、(B) 三、简答题 点的绝对速度为零 为绝对瞬心,否则为相对瞬心。今后将用符号p时表示构件人了间的瞬心。而由N个构件 (含机架)组成的机构的瞬心总数K应为:K=N(N.1)/2 2、1)由瞬心定义确定解心的位置:对于通过运动副直接相联的两构件间的解心,可由瞬心 定义直观地确定其位置,其方法如下 以转动副相联接的两构件,其瞬心就在转动副的中心处: 以移动副相联接的两构件,其瞬心位于垂直于导路方向的无穷远处: 以作纯滚动高副相联接的两构件,其瞬心就在接触点处; 以作滚动拖滑动高副相联接的两构件,其瞬心在过接触点高刷元素的公法线上 2借助三心定理确定瞬心的位置:对于不通过运动副直接相联的两构件间的瞬心位置, 可借 三心定理来确定:而三心定理是说:三个彼此作平面平行运动的构件的三个解心必位 于同一直线上。 四、分析计算题 1、解:为了确定构件4的角速度的大小,和方向, 首先需要求出绝对瞬心P45及相对瞬心P,的位置。 为便于找出所需瞬心可借助于顺心多边形(图b)的 帮助 在图示机构中,顺心P、 P、P P 故瞬心P4不在M点,而在过M点的公法线nn上的 某点处。 由图b可知,顺心P3位置在P公P2,的连线及 P、P钻连线的交点处 连接PB与P,的连线与公法线nn的交点即为 顺心P,的位置:再分别连接顺心 PsP:及顺心P5、P4两者的交点即为解心 P45
第二章 平面机构的运动分析 习题解答 一、填空题 1、相对速度; 2 、三心定理来; 3、两速度矢量的垂线的交点 二、判断题 (答 A 表示说法正确.答 B 表示说法不正确) 1、( B ); 2、( B ) 三、简答题 1、速度瞬心(简称瞬心):若该点是互作平面相对运动两构件上瞬时相对速度为零、或者说绝 对速度相等的重合点,故瞬心可定义为两构件上的瞬时等速重合点。若该点的绝对速度为零, 为绝对瞬心,否则为相对瞬心。今后将用符号 pij表示构件 i、j 间的瞬心。而由 N 个构件 (含机架)组成的机构的瞬心总数 K 应为:K = N (N - 1)/ 2 2、1)由瞬心定义确定瞬心的位置:对于通过运动副直接相联的两构件间的瞬心,可由瞬心 定义直观地确定其位置,其方法如下: 以转动副相联接的两构件,其瞬心就在转动副的中心处; 以移动副相联接的两构件,其瞬心位于垂直于导路方向的无穷远处; 以作纯滚动高副相联接的两构件,其瞬心就在接触点处; 以作滚动兼滑动高副相联接的两构件,其瞬心在过接触点高副元素的公法线上。 2)借助三心定理确定瞬心的位置:对于不通过运动副直接相联的两构件间的瞬心位置, 可借助三心定理来确定;而三心定理是说:三个彼此作平面平行运动的构件的三个瞬心必位 于同一直线上。 四、分析计算题 1、解:为了确定构件 4 的角速度的大小 4 和方向, 首先需要求出绝对瞬心 P45 及相对瞬心 P14 的位置。 为便于找出所需瞬心可借助于顺心多边形(图 b)的 帮助。 在图示机构中,顺心 P15 、P12 、P23 、P35 、P34 的位置已知,因构件I、4组成的高副M非纯滚动, 故瞬心 P14 不在M点,而在过M点的公法线nn上的 某点处。 由图b可知,顺心P13 位置在P12、P23 的连线及 P15、P35 连线的交点处。 连接P13 与P34 的连线与公法线nn的交点即为 顺心P14 的位置;再分别连接顺心 P15P14 及顺心P35、P34 两者的交点即为瞬心 P45

由于瞬心P14是构件I与4的等速重合点,而P45是构件4的绝对顺心,故 =PaPs/PaPs 因P1内分PP,故04与反向,即0,沿逆时针方向。 2解:由于哥氏加速度的大小2B3=20,'B2B3故 只有3与"2中任何一项为零,均无哥氏加速度存在。 由于在图b中@,=@,=0,故该机构在任何位置均无哥 氏加速度。而图a所示机构除四个特殊位置外,则有哥氏 加速度存在。无哥氏加速度的四个特殊位置是:当构件1、 3、4重合,B点处于最高和最底位置时,因此时v2=0: 当构件1与3彼此垂直,这时构件3处于最左边或最右边 位置,因此时,==0。 A
由于瞬心P14 是构件I与4的等速重合点,而P45 是构件 4 的绝对顺心,故 4 1 14 15 14 45 = P P P P / 因P14 内分 P P15 45 ,故 4 与 1 反向,即 4 沿逆时针方向。 2、解:由于哥氏加速度的大小 2 2 3 3 2 3 k a B B B B = 故 只有 3 与 B B2 3 v 中任何一项为零,均无哥氏加速度存在。 由于在图 b 中 2 3 = = 0 ,故该机构在任何位置均无哥 氏加速度。而图 a 所示机构除四个特殊位置外,则有哥氏 加速度存在。无哥氏加速度的四个特殊位置是:当构件 1、 3、4 重合,B 点处于最高和最底位置时,因此时 2 3 0 B B v = ; 当构件 1 与 3 彼此垂直,这时构件 3 处于最左边或最右边 位置,因此时 2 3 = = 0