
本章内容简介 第二章 3.1 机构运动分析的任务、目的和 方法 3.2 用速度瞬心法作机构速度分析 干面渐构的运动分新 3.3 用矢量方程图解法作机构的速 度分析及加速度分析 3.4 综合运用瞬心法和矢量方程图 解法对复杂机构进行速度分析 3.5 用解析法作机构的运动分析 世大学 KINJIANG UNIVERSITY 机械设计教研室
机原 理械 3.1 机构运动分析的任务、目的和 方法 3.2 用速度瞬心法作机构速度分析 3.3 用矢量方程图解法作机构的速 度分析及加速度分析 3.4 综合运用瞬心法和矢量方程图 解法对复杂机构进行速度分析 3.5 用解析法作机构的运动分析
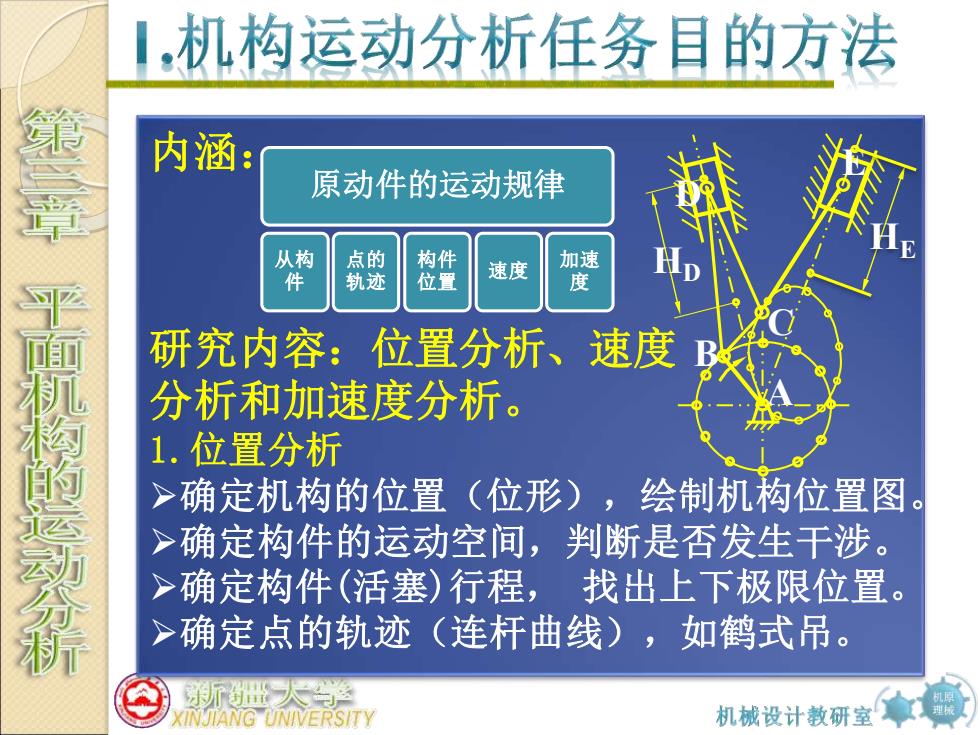
1,机构运动分析任务目的方法 内涵: 原动件的运动规律 从构 点的 构件 件 轨迹 位置 速度 加速 度 干面构的运动分新 研究内容:位置分析、速度 分析和加速度分析。 1.位置分析 >1 确定机构的位置(位形),绘制机构位置图。 >确定构件的运动空间,判断是否发生干涉。 >确定构件(活塞)行程,找出上下极限位置。 >确定点的轨迹(连杆曲线),如鹤式吊。 INJIANG UNIVERSITY 机械设计教研室
机原 理械 内涵: 研究内容:位置分析、速度 分析和加速度分析。 1.位置分析 ➢确定机构的位置(位形),绘制机构位置图。 ➢确定构件的运动空间,判断是否发生干涉。 ➢确定构件(活塞)行程, 找出上下极限位置。 ➢确定点的轨迹(连杆曲线),如鹤式吊。 原动件的运动规律 从构 件 点的 轨迹 构件 位置 速度 加速 度 A C B E D HE HD

1,机构运动分析任务目的方法 2.速度分析 >通过分析,了解从动件的速度变化规律是否 满足工作要求。如牛头刨 >为加速度分析作准备。 3.加速度分析的目的是为确定惯性力作 准备。方法: >图解法一简单、直观、精度低、求系列位置 时繁琐。 解析法一正好与以上相反。 实验法一试凑法,配合连杆曲线图册,用于 解决实现预定轨迹问题。 新世大学 KINJIANG UNIVERSITY 机械设计教研室
机原 理械 2.速度分析 ➢通过分析,了解从动件的速度变化规律是否 满足工作要求。如牛头刨 ➢为加速度分析作准备。 3.加速度分析的目的是为确定惯性力作 准备。方法: ➢图解法-简单、直观、精度低、求系列位置 时繁琐。 ➢解析法-正好与以上相反。 ➢实验法-试凑法,配合连杆曲线图册,用于 解决实现预定轨迹问题

2,速度瞬心法作机构速度分析 、 速度瞬心及其求法 l)速度瞬心(instantaneous centre of velocity)一两个作平面运动构件上速度相同 的一对重合点,在某一瞬时两构件相对于该 点作相对转动,该点称瞬时速度中心。 千面祈梅的运动分析 >相对瞬心(relative centre of velocit) 一 重合点绝对速度不为零。 >绝对瞬心(absolute centre0fle 一重合点绝对速度为零。 所世大学 机厚 KINJIANG UNIVERSITY 机械设计教研室 理械
机原 理械 一、速度瞬心及其求法 1)速度瞬心(instantaneous centre of velocity)-两个作平面运动构件上速度相同 的一对重合点,在某一瞬时两构件相对于该 点作相对转动 ,该点称瞬时速度中心。 ➢相对瞬心(relative centre of velocity) -重合点绝对速度不为零。 ➢绝对瞬心(absolute centre of velocity) -重合点绝对速度为零
2,速度瞬心法作机构速度分析 2)瞬心数目 若机构中有n个构件,则 第三章干面机构的运动分析 P13 每两个构件就有一个瞬心 .根据排列组合有 N=n(n-1)/2 P12 P23 构件数 4 5 6 8 瞬心数 6 10 15 28 世大 KINJIANG UNIVERSITY 机械设计教研室拿
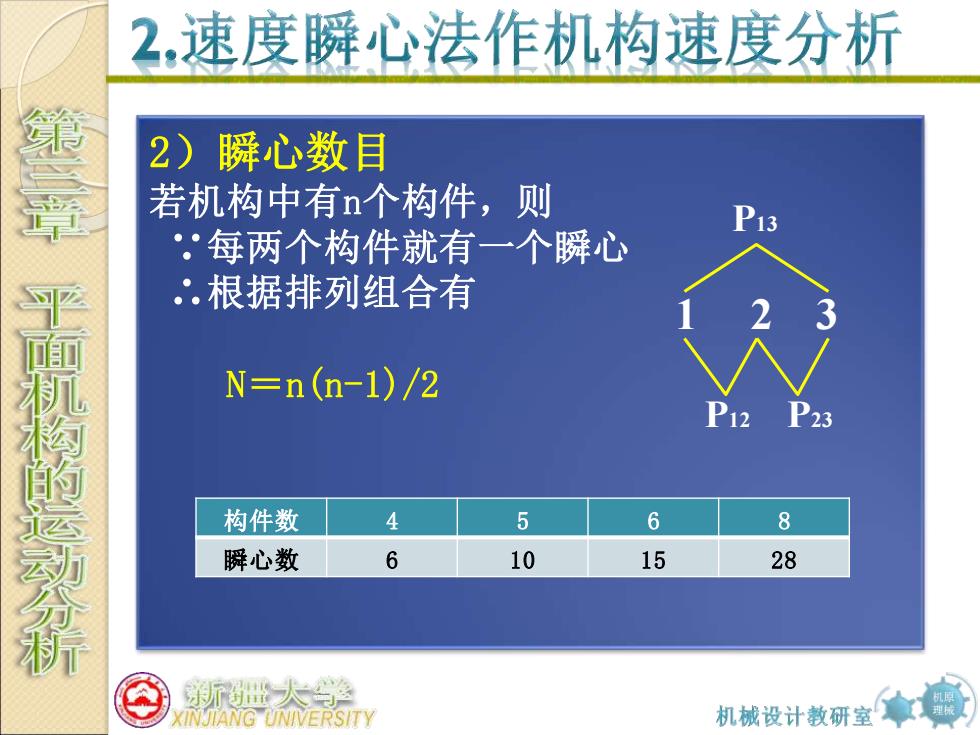
机原 理械 2)瞬心数目 若机构中有n个构件,则 ∵每两个构件就有一个瞬心 ∴根据排列组合有 N=n(n-1)/2 构件数 4 5 6 8 瞬心数 6 10 15 28 P12 P23 P13 1 2 3
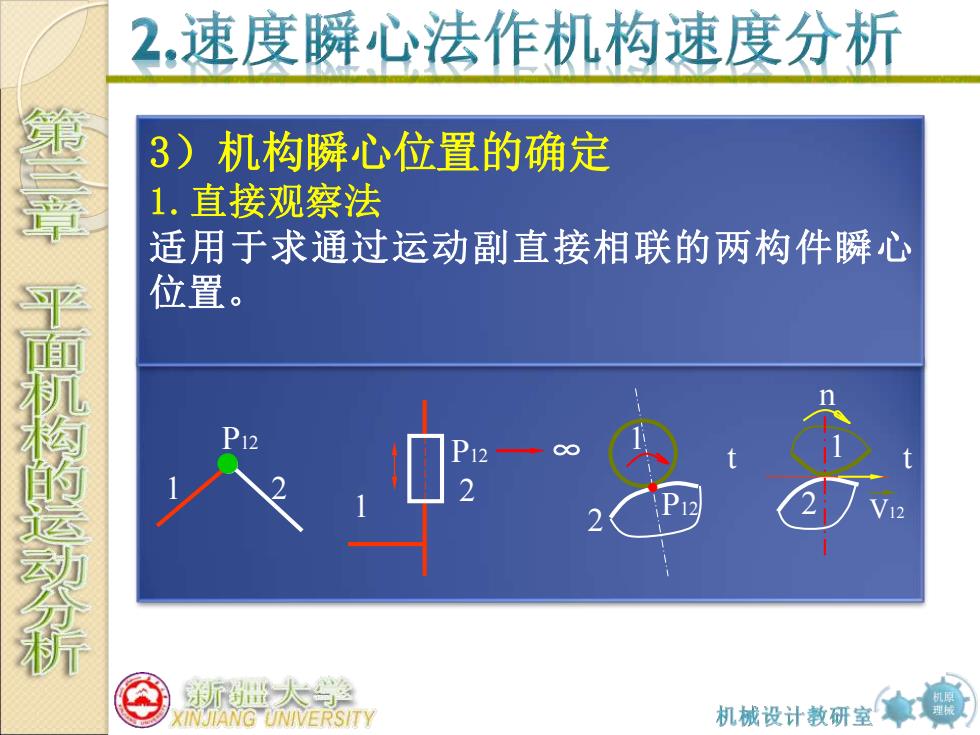
2,速度瞬心法作机构速度分析 3)机构瞬心位置的确定 1.直接观察法 适用于求通过运动副直接相联的两构件瞬心 位置。 干面机校的运动分析 斯世大 KINJIANG UNIVERSITY 机械设计教研室拿
机原 理械 3)机构瞬心位置的确定 1.直接观察法 适用于求通过运动副直接相联的两构件瞬心 位置。 1 2 P12 1 2 P12 ∞ 1 2 P12 t t 1 2 n V12
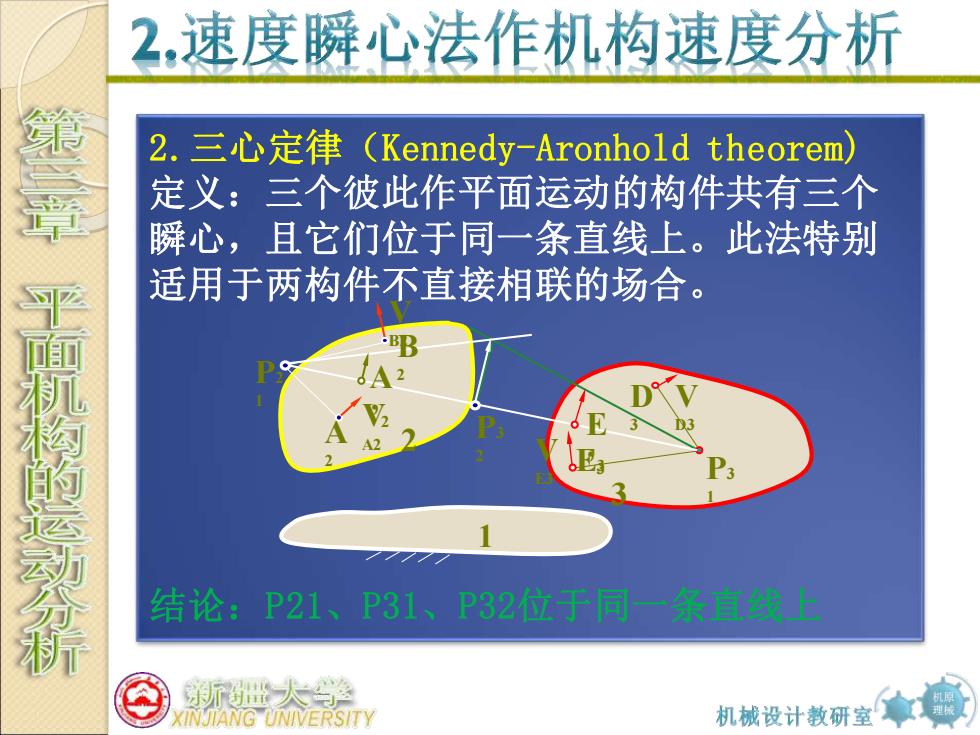
2,速度瞬心法作机构速度分析 2.三心定律(Kennedy-Aronhold theorem), 定义:三个彼此作平面运动的构件共有三个 瞬心,且它们位于同一条直线上。此法特别 适用于两构件不直接相联的场合。 干面瓶校的运动分析 结论:P21、P31、P32位于同一条直线自 新世大学 KINJIANG UNIVERSITY 机械设计教研室拿
机原 理械 2.三心定律(Kennedy-Aronhold theorem) 定义:三个彼此作平面运动的构件共有三个 瞬心,且它们位于同一条直线上。此法特别 适用于两构件不直接相联的场合。 结论:P21、P31、P32位于同一条直线上 作者:潘存云教授 1 2 3 P2 1 P3 1 E3 D 3 V E3 V D3 A 2 V A2 V B2 A ’ 2 E ’ 3 P3 2 B 2
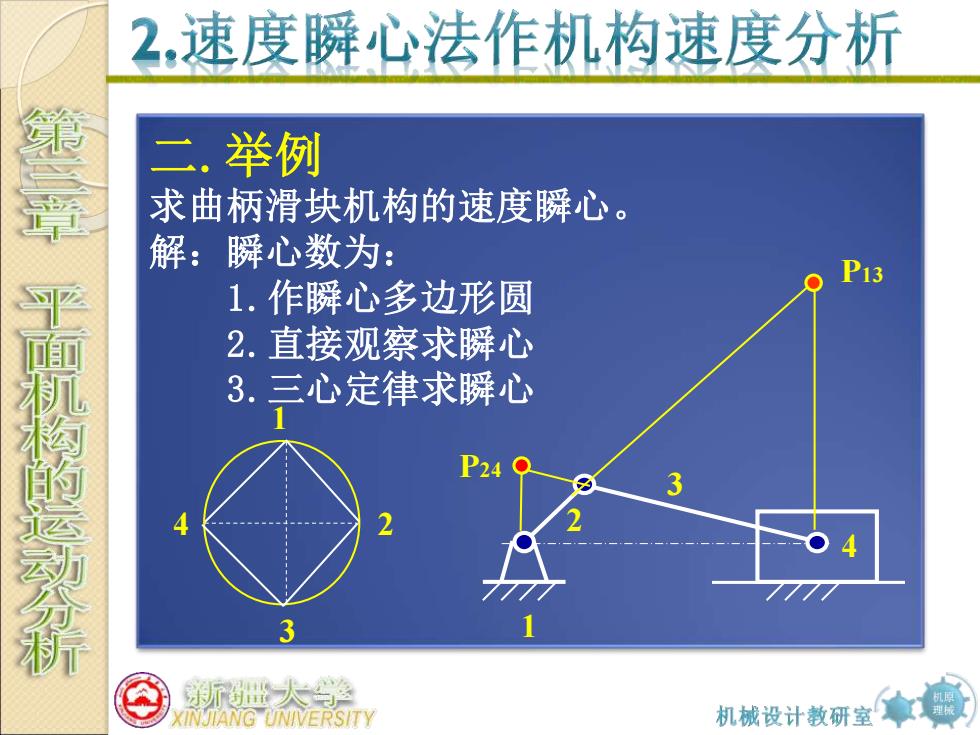
2,速度瞬心法作机构速度分析 二.举例 求曲柄滑块机构的速度瞬心。 解:瞬心数为: 1.作瞬心多边形圆 2.直接观察求瞬心 干面机检胞运动分析 3.三心定律求瞬心 P24 新世大学 KINJIANG UNIVERSITY 机械设计教研室拿】
机原 理械 二 .举例 求曲柄滑块机构的速度瞬心 。 解:瞬心数为: 1.作瞬心多边形圆 2.直接观察求瞬心 3.三心定律求瞬心 3 2 1 4P13 P24 1 2 3 4

2,速度瞬心法作机构速度分析 三、速度瞬心在机构速度分析中的应用 1.求线速度2.求角速度3.求传动比 四.用瞬心法解题步骤 >绘制机构运动简图 >求瞬心的位置 干面沟的运动分析 >求出相对瞬心的速度 >求构件绝对速度V或角速度⊙ 五.瞬心法的优缺点 >适合于求简单机构的速度,机构复杂时因瞬 心数急剧增加而求解过程复杂 >有时瞬心点落在纸面外 >仅适于求速度V,使应用有一定局限性 KINJIANG UNIVERSITY 机械设计教研室拿】
机原 理械 三、速度瞬心在机构速度分析中的应用 1.求线速度 2.求角速度 3.求传动比 四.用瞬心法解题步骤 ➢绘制机构运动简图 ➢求瞬心的位置 ➢求出相对瞬心的速度 ➢求构件绝对速度V或角速度ω 五.瞬心法的优缺点 ➢适合于求简单机构的速度,机构复杂时因瞬 心数急剧增加而求解过程复杂 ➢有时瞬心点落在纸面外 ➢仅适于求速度V,使应用有一定局限性
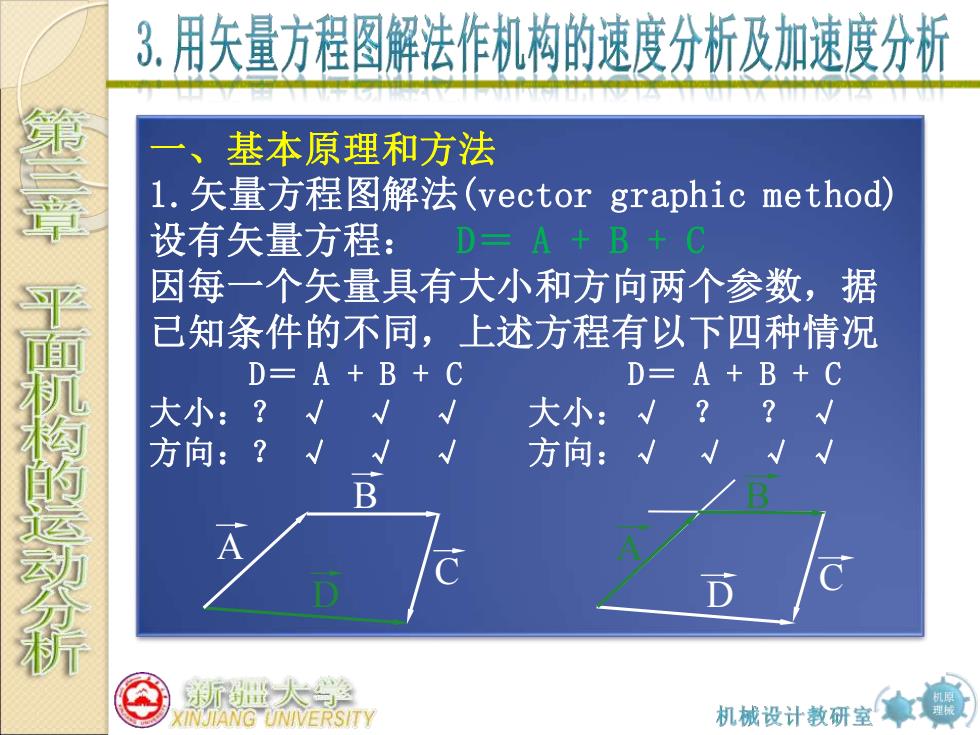
3.用矢量方程图解法作机构的速度分析及加速度分析 基本原理和方法 l.矢量方程图解法(vector graphic method) 设有矢量方程: D=A +B+C 因每一个矢量具有大小和方向两个参数,据 已知条件的不同,上述方程有以下四种情况 D=A +B+C D=A+B+C 上面瓶构的运动分析 大小:?√ 大小:√ 方向:? 方向: 新世大学静 KINJIANG UNIVERSITY 机械设计教研室
机原 理械 一、基本原理和方法 1.矢量方程图解法(vector graphic method) 设有矢量方程: D= A + B + C 因每一个矢量具有大小和方向两个参数,据 已知条件的不同,上述方程有以下四种情况 D= A + B + C D= A + B + C 大小:? √ √ √ 大小:√ ? ? √ 方向:? √ √ √ 方向:√ √ √ √ D A B C C D A B