
本章内容简介 7.1 概述 7.2 机械的运动动方程式 7.3 机械运动方程式的求解 7.4 稳定运转状态下机械的周期 性速度波动及其调节 7.5 机械的非周期性速度波动及 其调节 7.6 考虑构件弹性时的机械动力 学简介 玩世大 XINJIANG UNIVERSITY 机械设计教研室拿夏
机原 理械 7.1 概述 7.2 机械的运动动方程式 7.3 机械运动方程式的求解 7.4 稳定运转状态下机械的周期 性速度波动及其调节 7.5 机械的非周期性速度波动及 其调节 7.6 考虑构件弹性时的机械动力 学简介

,概述 研究内容及目的 研究在外力作用下机械的真实运动规律,目的是 为运动分析作准备。 研究机械运转速度的波动及其调节方法,目的是 使机械的转速在允许范围内波动,而保证正常工 作。 设计新的机械,或者分析现有机械的工作性能时,往往想知道机械运转的稳定性、构件的 惯性力以及在运动副中产生的反力的大小、Vxa的大小,因此要对机械进行运动分析。 而前面所介绍的运动分析时,都假定运动件作匀速运动(o=const)。但在大多数情况下, o≠const,而是力、力矩、机构位置、构件质量、转动惯量等参数的函数:o=F(P、M、 ”、J)。只有确定了的原动件运动o的变化规律之后,才能进行运动分析和力分析,从 而为设计新机械提供依据。这就是研究机器运转的目的。 所世大学 KINJIANG UNIVERSITY 机械设计教研室
机原 理械 一、研究内容及目的 ➢ 研究在外力作用下机械的真实运动规律,目的是 为运动分析作准备。 ➢ 研究机械运转速度的波动及其调节方法,目的是 使机械的转速在允许范围内波动,而保证正常工 作。 设计新的机械,或者分析现有机械的工作性能时,往往想知道机械运转的稳定性、构件的 惯性力以及在运动副中产生的反力的大小、Vmax amax的大小,因此要对机械进行运动分析。 而前面所介绍的运动分析时,都假定运动件作匀速运动(ω=const)。但在大多数情况下, ω≠const,而是力、力矩、机构位置、构件质量、转动惯量等参数的函数:ω=F(P、M、 φ、m、J)。只有确定了的原动件运动ω的变化规律之后,才能进行运动分析和力分析,从 而为设计新机械提供依据。这就是研究机器运转的目的
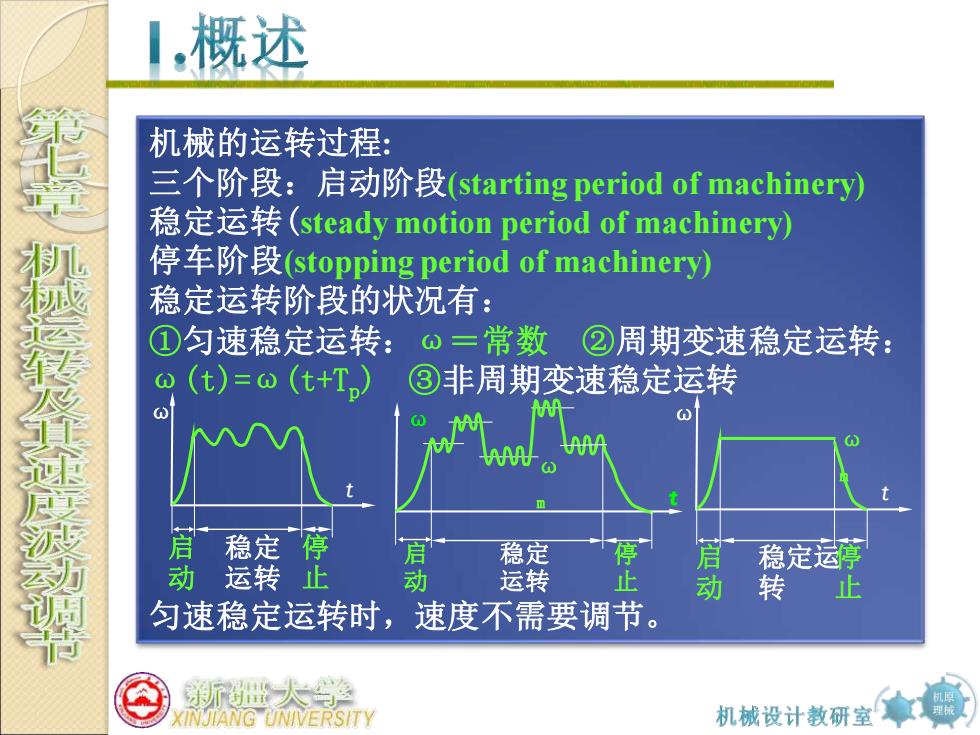
1,概述 机械的运转过程: 三个阶段:启动阶段(starting period of machinery) 稳定运转(steady motion period of machinery)) 停车阶段(stopping period of machinery) 稳定运转阶段的状况有: ①匀速稳定运转:o三常数 ②周期变速稳定运转: (t)=(t+T) ③非周期变速稳定运转 稳定 停 稳定 停 定运 运转 动 运转 动 转 匀速稳定运转时,速度不需要调节。 世大 KINJIANG UNIVERSITY 机械设计教研室
机原 理械 机械的运转过程: 三个阶段:启动阶段(starting period of machinery) 稳定运转(steady motion period of machinery) 停车阶段(stopping period of machinery) 稳定运转阶段的状况有: ①匀速稳定运转:ω=常数 ②周期变速稳定运转: ω(t)=ω(t+Tp) ③非周期变速稳定运转 匀速稳定运转时,速度不需要调节。 稳定 运转 启 动 t ω 停 止 启 动 ω m t ω 稳定 运转 停 止 ω m t ω 稳定运 转 启 动 停 止

概述 速度波动产生的不良后果 ①在运动副中引起附加动压力, 加剧磨损,使工作可 靠性降低。 ②引起弹性振动,消耗能量,使机械效率降低。 ③影响机械的工艺过程,使产品质量下降。 ④载荷突然减小或增大时,发生飞车或停车事故。 为了减小这些不良影响,就必须对速度波动范围进行 调节。 二、速度波动调节的方法 1.对周期性速度波动,可在转动轴上安装一个质量较 大的回转体(俗称飞轮)达到调速的目的。 2.对非周期性速度波动,需采用专门调速器才能调节。 本章仅讨论飞轮调速问题。 KINJIANG UNIVERSITY 机械设计教研室
机原 理械 速度波动产生的不良后果: ①在运动副中引起附加动压力,加剧磨损,使工作可 靠性降低。 ②引起弹性振动,消耗能量,使机械效率降低。 ③影响机械的工艺过程,使产品质量下降。 ④载荷突然减小或增大时,发生飞车或停车事故。 为了减小这些不良影响,就必须对速度波动范围进行 调节。 二、速度波动调节的方法 1.对周期性速度波动,可在转动轴上安装一个质量较 大的回转体(俗称飞轮)达到调速的目的。 2.对非周期性速度波动,需采用专门调速器才能调节。 本章仅讨论飞轮调速问题

1,概述 三、作用在机械上的驱动力和生产阻力 蒸汽机与内然机发出的驱动力是活塞位置的函数: MM(s) 电动机提供的驱动力矩是转子角速度ω的函数: MM(o) 机械特性(mechanical behavior)曲 线一原动机发出的驱动力(或力矩 )与运动参数之间的函数关系曲线。 工程上常将特性曲线作近似处理, 如用通过额定转矩点N的直线NC代 工作转一 替曲线NC。 交流异步电动机的机械特性曲线 MMn@o一o/(@0-o 其中M,一额定转矩、⊙n一额定角速度、o,一同步角速度 世大 KINJIANG UNIVERSITY 机械设计教研室
机原 理械 三、作用在机械上的驱动力和生产阻力 蒸汽机与内然机发出的驱动力是活塞位置的函数: Md=M(s) 电动机提供的驱动力矩是转子角速度的函数: Md=M() 机械特性(mechanical behavior)曲 线-原动机发出的驱动力(或力矩 )与运动参数之间的函数关系曲线。 工程上常将特性曲线作近似处理, 如用通过额定转矩点N的直线NC代 替曲线NC。 Md=Mn (0-)/ (0-n ) 其中Mn-额定转矩 、n -额定角速度、0 -同步角速度 ω M d B N 交流异步电动机的机械特性曲线 A ω C n 工作转速ω

1概述 生产阻力取决于生产工艺过程的特点,有如下几种情 况: >生产阻力为常数,如车床; >生产阻力为机构位置的函数,如压力机; >生产阻力为执行构件速度的函数,如鼓风机、 搅拌 机等; >生产阻力为时间的函数,如球磨机、揉面机等; 本课程所讨论机械在外力作用下运动时,假定外力为已知。 所量大 KINJIANG UNIVERSITY 机械设计教研室 理械
机原 理械 生产阻力取决于生产工艺过程的特点,有如下几种情 况: ➢生产阻力为常数,如车床; ➢生产阻力为机构位置的函数,如压力机; ➢生产阻力为执行构件速度的函数,如鼓风机、搅拌 机等; ➢生产阻力为时间的函数,如球磨机、揉面机等; 本课程所讨论机械在外力作用下运动时,假定外力为已知
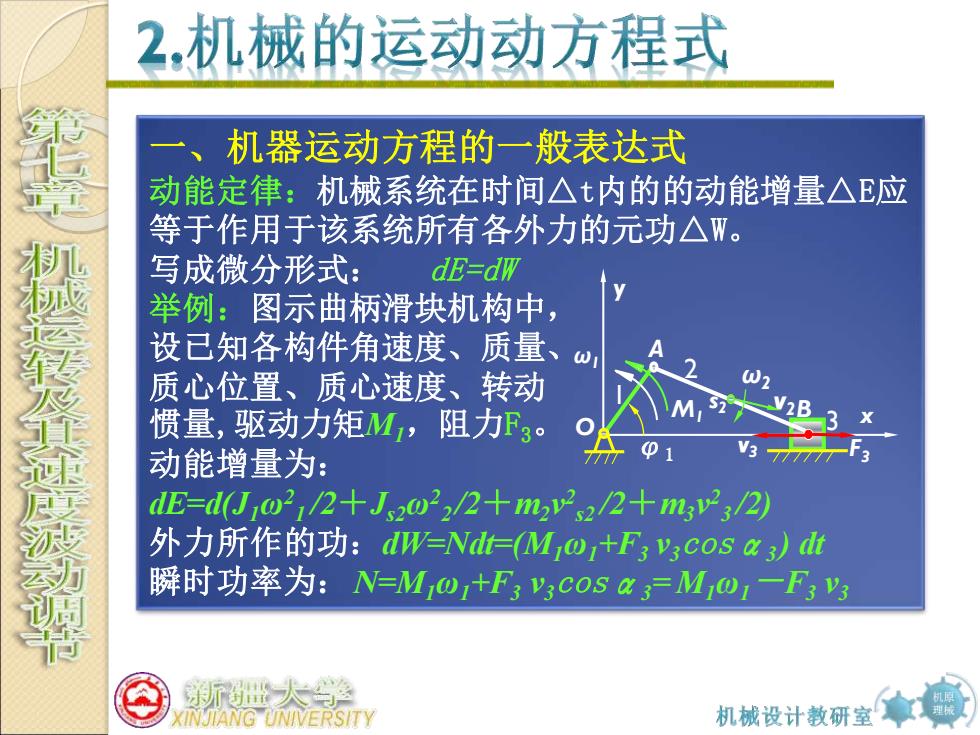
2,机械的运动动方程式 一、机器运动方程的一般表达式 动能定律:机械系统在时间△t内的的动能增量△E应 等于作用于该系统所有各外力的元功△W。 写成微分形式: dE=dW 举例:图示曲柄滑块机构中, 设已知各构件角速度、质量、 质心位置、质心速度、转动 惯量,驱动力矩M,阻力F3。 M V2B ● 动能增量为: 77 dE=d0o2/2十Jo2/2+m22/2+32 外力所作的功:dW-Ndt-(Mj@j+F,cosx 瞬时功率为:N=M+F3 v3cos a 3=M@1一F 世大学 KINJIANG UNIVERSITY 机械设计教研室
机原 理械 一、机器运动方程的一般表达式 动能定律:机械系统在时间△t内的的动能增量△E应 等于作用于该系统所有各外力的元功△W。 写成微分形式: dE=dW 举例:图示曲柄滑块机构中, 设已知各构件角速度、质量、 质心位置、质心速度、转动 惯量,驱动力矩M1,阻力F3。 动能增量为: dE=d(J1ω2 1 /2+Js2ω2 2 /2+m2v 2 s2 /2+m3v 2 3 /2) 外力所作的功:dW=Ndt=(M1ω1+F3 v3cosα3 ) dt 瞬时功率为:N=M1ω1+F3 v3cosα3= M1ω1-F3 v3 x y 1 2 3 s2 O A B φ1 ω2 M1 ω1 v2 F3 v3

2,机械的运动动方程式 运动方程为: d0o22十J222十n22/2十m,/2=0M01F,y)dt 推广到一般,设有个活动构件,用E表示其动能。 则有: E=之E 二2(m心+2) 设作用在构件i上的外力为F,力矩M为,力F,作用 点的速度为y。则瞬时功率为: N-N. a为F与之间的夹角,M,与δ方向相同时取十”,相反时取“一” 机器运动方程的一般表达式为: Fm,cosa+】 ±M,o,ld 斯世大学 INJIANG UNIVERSITY 机械设计教研室 理械
机原 理械 运动方程为: d(J1ω2 1 /2+Jc2ω2 2 /2+m2v 2 c2 /2+m3v 2 3 /2)=(M1ω1-F3 v3 )dt 推广到一般,设有n个活动构件,用Ei表示其动能。 则有: 设作用在构件i上的外力为Fi,力矩Mi为,力Fi 作用 点的速度为vi。则瞬时功率为: αi为Fi与vi之间的夹角,Mi与ωi方向相同时取“+”,相反时取“-” 机器运动方程的一般表达式为: = = n i E Ei 1 = = n i N Ni 1 = = + n i mi vi Jci i 1 2 2 ) 2 1 2 1 ( = = = + n i n i i i i Mi i Fv 1 1 cos )] 2 1 2 1 [ ( 1 2 2 = + n i i i ci i d m v J Fv M dt n i n i i i i i i [ cos ] 1 1 = = = +

2,机械的运动动方程式 二、机械系统的等效动力学模型 上例有结论: dW1o2十Je2o2十m2c22十m32)=M1—FE v:)dt 重写为 do2/2(J+Je2o22/o21十m222/o21十3o2)] =ω,M一F3y3@)dt 右边小括号内的各项具有转动惯量的量纲, 左边小括号内的各项具有力矩的量纲。 令: J(Ji十J2022o2 M=M1-F3v3/0 则有:d3Jo22=M.o,dMd② 世大学 KINJIANG UNIVERSITY 机械设计教研室
机原 理械 二、机械系统的等效动力学模型 上例有结论: d(J1ω2 1 /2+Jc2ω2 2 /2+m2v 2 c2 /2+m3v 2 3 /2) =(M1ω1-F3 v3 )dt 重写为: d[ω2 1 /2 (J1+Jc2ω2 2 /ω2 1+m2v 2 c2 /ω2 1+m3v 2 3 /ω2 1 ) ] =ω1 (M1 -F3 v3 /ω1 )dt 右边小括号内的各项具有转动惯量的量纲, 左边小括号内的各项具有力矩的量纲。 令: Je=( J1+Jc2ω2 2 /ω2 1.) M e = M1-F3 v3 /ω1 则有: d(Jeω2 1 /2 )= Meω1 dt=Medφ
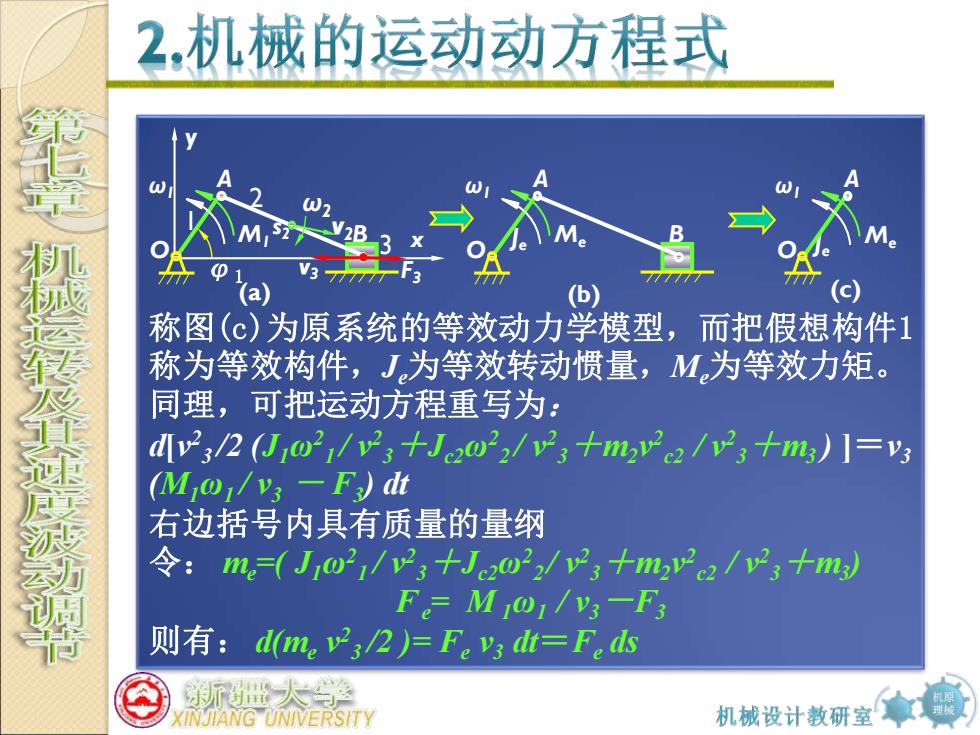
2,机械的运动动方程式 称图(c)为原系统的等效动力学模型,而把假想构件1 称为等效构件,J为等效转动惯量,M为等效力矩。 同理,可把运动方程重写为: d,2(Jo21/w2,+Je22十m2/v3十%)]=v3 (M0/v3-F)dt 右边括号内具有质量的量纲 令:m(Jo2/2十e2o2272十m22/,大m F=M9/3一F 则有:dme2,2)=F。dt=Fd INJIANG UNIVERSITY 机械设计教研室
机原 理械 称图(c)为原系统的等效动力学模型,而把假想构件1 称为等效构件,Je为等效转动惯量,Me为等效力矩。 同理,可把运动方程重写为: d[v 2 3 /2 (J1ω2 1 / v2 3+Jc2ω2 2 / v2 3+m2v 2 c2 / v2 3+m3 ) ]=v3 (M1ω1 / v3 - F3 ) dt 右边括号内具有质量的量纲 令: me=( J1ω2 1 / v2 3+Jc2ω2 2 / v2 3+m2v 2 c2 / v2 3+m3 ) Fe = M 1ω1 / v3-F3 则有: d(me v 2 3 /2 )= Fe v3 dt=Fe ds (a) (b) J x e y 1 2 3 s2 O A B φ1 ω2 M1 ω1 v2 F3 v3 O A Me B ω1 Me (c) J O e ω A 1