
Chapter 5 Digital transmission through the AWGN channel by Prof.XIAOFENG LI SICE,UESTC UESTC-Digital transmission through the AWGN channel Prof李晓峰 1

Introduction In this chapter,we focus on how to transmit digital info signals with waveforms. The topics include: 1. Geometric representation of sig waveforms; 2.Diff types of waveforms for digital transmissions; 3.Optimal reception; 4. Performance evaluation on the AWGN channel 5. Comparison of the methods. UESTC-Digital transmission through the AWGN channel Prof李晓峰 3

Contents 16 Hrs ■Introduction Geometric rep.of the sig waveforms Pulse amplitude modulation 2-d signal waveforms M-d signal waveforms Opt.reception for the sig.in AWGN Optimal receivers and probs of err UESTC-Digital transmission through the AWGN channel Prof李晓峰 4

5.1 Geometric rep.of the sig waveforms 1.Review of the Vectors and Vector Space Concepts: ·length and direction Geometric representation u+V=(4,+,42+y 。 Coordinates u=(u,42}-----------二7 v=(Vx,V,) ·vector addition, v=(,) 。 length calculation ·dot/inner products 。 basis vectors:i and j 。 Algebraic representation,v=v xi+vx j Dimensions:2-space,3-space,N-space UESTC-Digital transmission through the AWGN channel Prof李晓峰 5

5.1 Geometric rep.of the sig waveforms 1.Review of the Vectors and Vector Space Let B=fe,...,ey}be an orthonormal basis for a N dimensional vector space RV. If v is any vector in the space,then it can be written uniquely in the form V=a1e1+a2e2+…+awev a,...,ay are called the coordinates of v. e2=j a +■,+,+ 02 u=(m V= y=(w, aN e1= UESTC-Digital transmission through the AWGN channel Prof李晓峰 6

5.1 Geometric rep.of the sig waveforms 1.Review of the Vectors and Vector Space With the dot product (or inner product),denotes as'',a coordinate is calculated by following, 'e2=j a;=v.e +年=+:1+的 = Because, v= v.e;=(ae+ae2+...+avex).e; projection e:=i -a(ee:)+a(e2.e:)+...+a(e;e)...+av(ev.e;) =ax0+a,x0++a×0+aw×0 =a; orthonormal basis UESTC-Digital transmission through the AWGN channel Prof李晓峰 7

5.1 Geometric rep.of the sig waveforms 1.Review of the Vectors and Vector Space B+V=a,+,:+ With coordinates,we have, V-U 1.The inner product u=∑ 2.The norm 州= 3. The distance d=y-=V∑(y-4)月 UESTC-Digital transmission through the AWGN channel Prof李晓峰 8
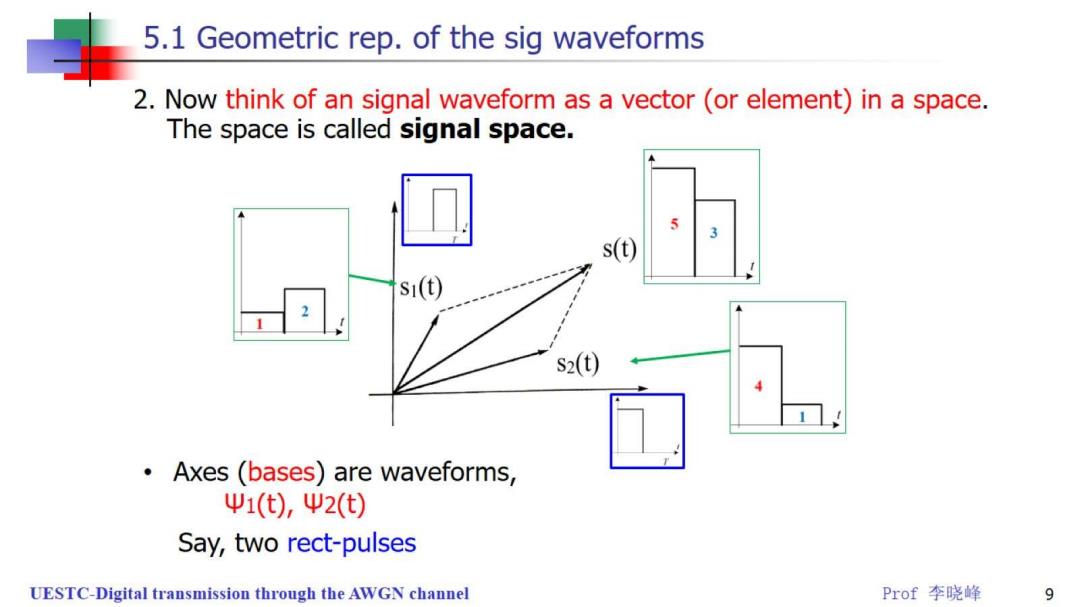
5.1 Geometric rep.of the sig waveforms 2.Now think of an signal waveform as a vector (or element)in a space. The space is called signal space. 3 s(t) S1() S2(0) Axes (bases)are waveforms, Ψ1(t),Ψ2(t) Say,two rect-pulses UESTC-Digital transmission through the AWGN channel Prof李晓峰 9
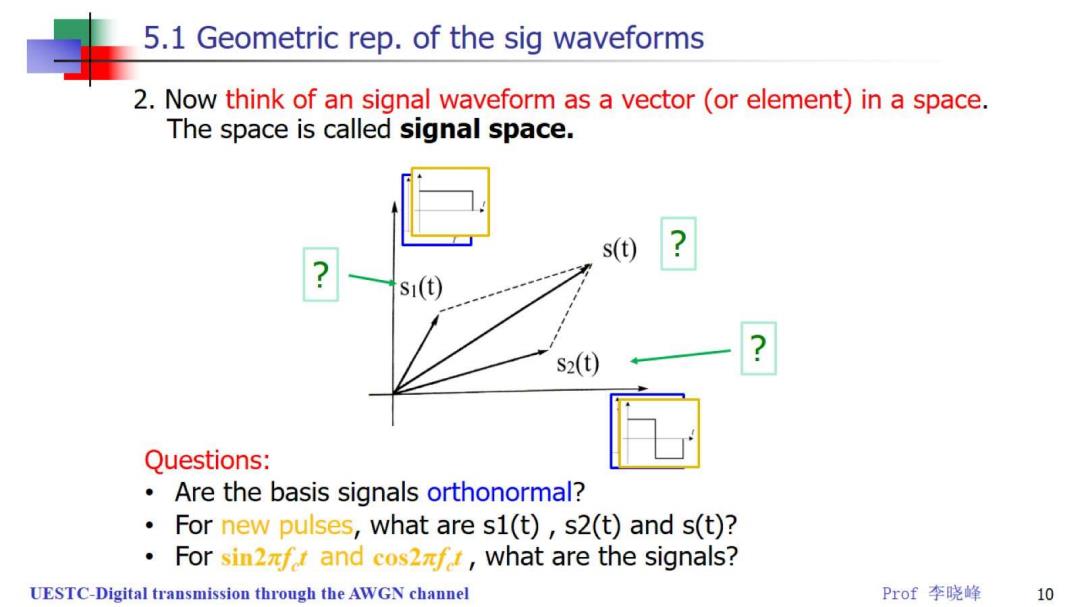
5.1 Geometric rep.of the sig waveforms 2.Now think of an signal waveform as a vector (or element)in a space. The space is called signal space. s() S1(t) S2(t) Questions: Are the basis signals orthonormal? For new pulses,what are s1(t),s2(t)and s(t)? For sin2fr and cos2f,what are the signals? UESTC-Digital transmission through the AWGN channel Prof李晓峰 10

5.1 Geometric rep.of the sig waveforms 2.Now think of an signal waveform as a vector (or element)in a space. The inner product in signal space. Let s,S1,S2 denotes(1),s(1),s2 (1),and define the inner product of S and s2 as ss2=s,()s,(0d s() S1(t) S2() UESTC-Digital transmission through the AWGN channel Prof李晓峰 11