
Contents 16 Hrs Introduction Geometric rep.of the sig waveforms Pulse amplitude modulation 2-d signal waveforms M-d signal waveforms ■Opt.reception for the sig.in AWGN ■Optimal receivers and probs of err UESTC-Digital transmission through the AWGN channel Prof李晓峰 2

5.5 Opt.reception for the sig.In AWGN In the nth interval,the process is as follows, {,an,} {,an} The topics are: ()1)The Correlation-Demodulators s(2)The MF-Demodulators 3)The Theory of Optimum Detectors 5.6 Typical Optimal Receivers 。 Binary signals r(t) Carrier-amp(1-D signals) Carrier-phs (2-D signals) It is convenient to divide the receiv QAM (2-D signals) 1)Demodulator:produce an obse FSK (M-D orthogonal signals) 2)Detector:estimate the sym from the observation UESTC-Digital transmission through the AWGN channel Prof李晓峰 3

5.5.2 The optimum detector Detector:estimate the sym from the observation What is the problem in the detector With observation r=(,..,)in hand,we recall that r=s +n and picture it. ·r=s1+n Digital Communications Prof李晓峰 4

5.5.2 The optimum detector Detector:estimate the sym from the observation What is the problem in the detector With observation r=(,..,)in hand,we recall that r=s,+n and picture it. r=s+n Digital Communications Prof李晓峰 5
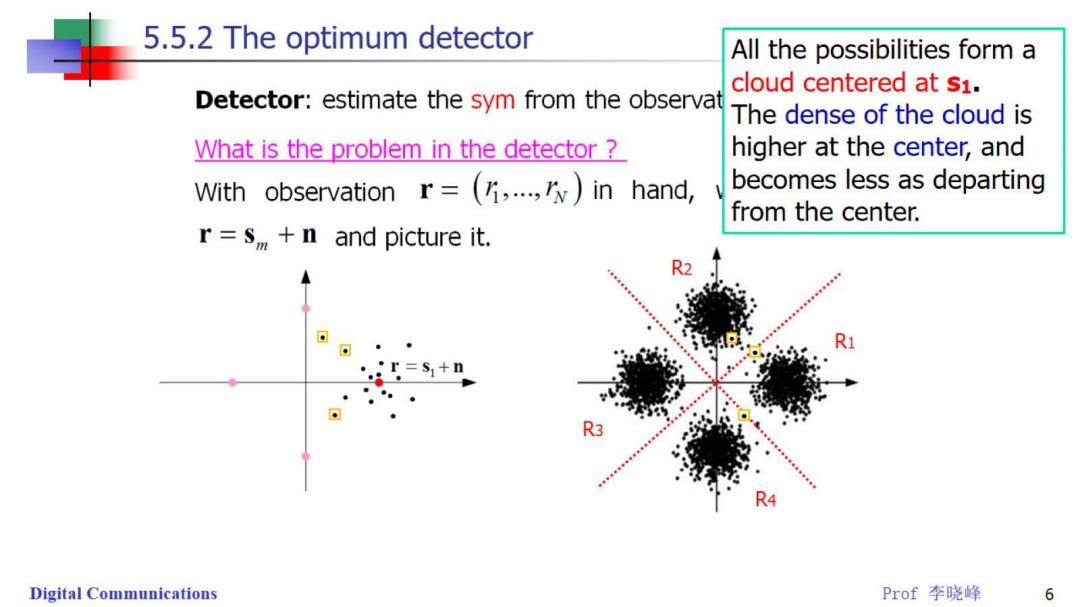
5.5.2 The optimum detector All the possibilities form a cloud centered at s1. Detector:estimate the sym from the observat The dense of the cloud is What is the problem in the detector higher at the center,and With observation r=(,..in hand, becomes less as departing from the center. r=s +n and picture it. R2 。r=s1+n R3 Digital Communications Prof李晓峰 6

5.5.2 The optimum detector The dense indicates basically the probability density or r. What is a good detector ?----Make error as less as posible How to measure error ?----Probability of error Let R be the region in the space for which we select s, Re be the complement of R.They are decided by the criterion. R3 The average probability of errors is, E-P(e)=1-ES P(.Ir)f(r)dr P(successs)=P(s,Ir)f(r)dr where,P(s,r)is the prob that s has been transmitted on the reception of r f(r)is the unconditional pdf of r. Digital Communications Prof李晓峰

5.5.2 The optimum detector What is the best detector P.is minimum when R corresponds to max P(sr). That lead to MAP criterion as follows. P.=P(e)=1->[P(slr)f(r)dr Digital Communications Prof李晓峰 8

5.5.2 The optimum detector What is the best detector P is minimum when R corresponds to max P(s r). That lead to MAP criterion as follows. The Optimum Detector: P=P(e)=l-∑j。P(smlr)fr)dr MAP: Max a posterior probability ML: Maximum-likelihood Min-Dist Minimum-distance Max-Corr:Maximum Correlation Maximum a posterior probability (MAP):to select the s,that max the P(sr).Denoted by, s=arg max,.(P(s Ir) Note that P(s,r)is often called a posterior probability. Digital Communications Prof李晓峰 9

5.5.3 The optimum detector Using Bayes'rule, P(sr)=f(rIs)P(s) f(r) where,f(rs,)is the condi pdf of r given s; P(s)is prob of transmittings,called priori probability Let PM(r,s)=f(rls)P(s) MAP is equivalent to:sm=arg max、PM(r,sm) The Optimum Detector: Maximum a posterior probability (MAP):to s MAP: Max a posterior probability s,that max the P(sr).Denoted by, ML: Maximum-likelihood Min-Dist Minimum-distance s=arg maxs.(P(s Ir) Max-Corr:Maximum Correlation Note that P(s,r)is often called a posterior probability. UESTC-Digital transmission through the AWGN channel Prof李晓峰 10

5.5.3 The optimum detector Note that f(rs,)is usually called likelihood function. Maximum-likelihood (ML):to select the s,that max the f(rs,). Denoted by, =arg max,(f(rls) Obviously,when the symbols are equally probable,we have,ML=MAP Equally-probable case is very common,thus ML is widely used in practical. Let PM(r,s)=f(rs)P(s) MAP is equivalent to:sm=arg max、PM(r,sm) The Optimum Detector: Maximum a posterior probability (MAP):to s MAP: Max a posterior probability s,that max the P(sr).Denoted by, ML: Maximum-likelihood Min-Dist Minimum-distance s =arg maxs (P(sIr) Max-Corr:Maximum Correlation Note that P(s,r)is often called a posterior probability. UESTC-Digital transmission through the AWGN channel Prof李晓峰 11