
5.6 Binary Baseband: BPAM (antipodal,unipolar),Orthogonal signaling; Passband: BPSK, OOK or BASK, BFSK(Orthogonal) M-ary,1-D signaling Baseband:MPAM Passband: MASK M-ary,2-D signaling (Passband) MPSK, QAM UESTC-Digital transmission through the AWGN channel Prof李晓峰 2
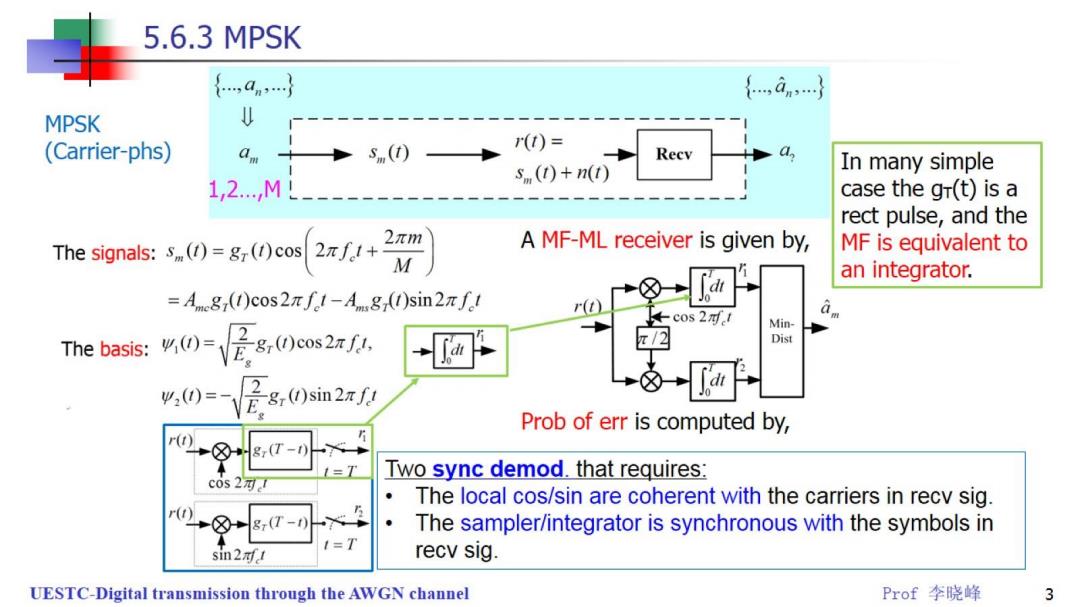
5.6.3 MPSK {,an} {,an,} MPSK (Carrier-phs) s(t) r(t)= Recv s (t)+n(t) In many simple 1,2.Ml case the gr(t)is a rect pulse,and the The signals:s()=gr()cos x+ A MF-ML receiver is given by, MF is equivalent to an integrator. =Ang()cos2πfc1-Ang()sin2πfl r() ←cos2对l Min- (gcos2. Dist The basis: %0=是,0si如2 Prob of err is computed by, r(t) ⑧8(T-0 L=T Two sync demod.that requires: c0s2河 The local cos/sin are coherent with the carriers in recv sig. 。 The sampler/integrator is synchronous with the symbols in recv sig. UESTC-Digital transmission through the AWGN channel Prof李晓峰 3
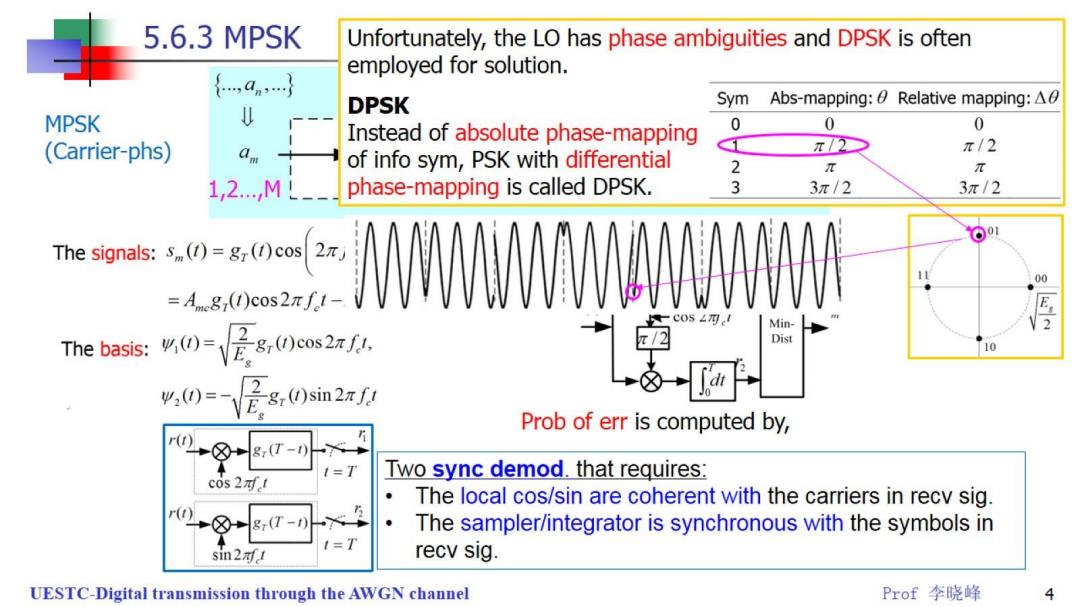
5.6.3 MPSK Unfortunately,the LO has phase ambiguities and DPSK is often employed for solution. DPSK Sym Abs-mapping:Relative mapping:A0 MPSK Instead of absolute phase-mapping 0 0 0 (Carrier-phs) π2 π/2 of info sym,PSK with differential 2 π π 1,2,ML-- phase-mapping is called DPSK. 3 3π/2 3π/2 1 The signals:s()=gr()cos 00 =Amg(I)cos2πf1 Min- 2 The basis: %0-28,0cos2 Dist %0=是,0sm2 Prob of err is computed by, r(t) 1=T Two sync demod.that requires: c0s21 The local cos/sin are coherent with the carriers in recv sig. r→⑧8,T- The sampler/integrator is synchronous with the symbols in sin2ft recv sig. UESTC-Digital transmission through the AWGN channel Prof李晓峰 4
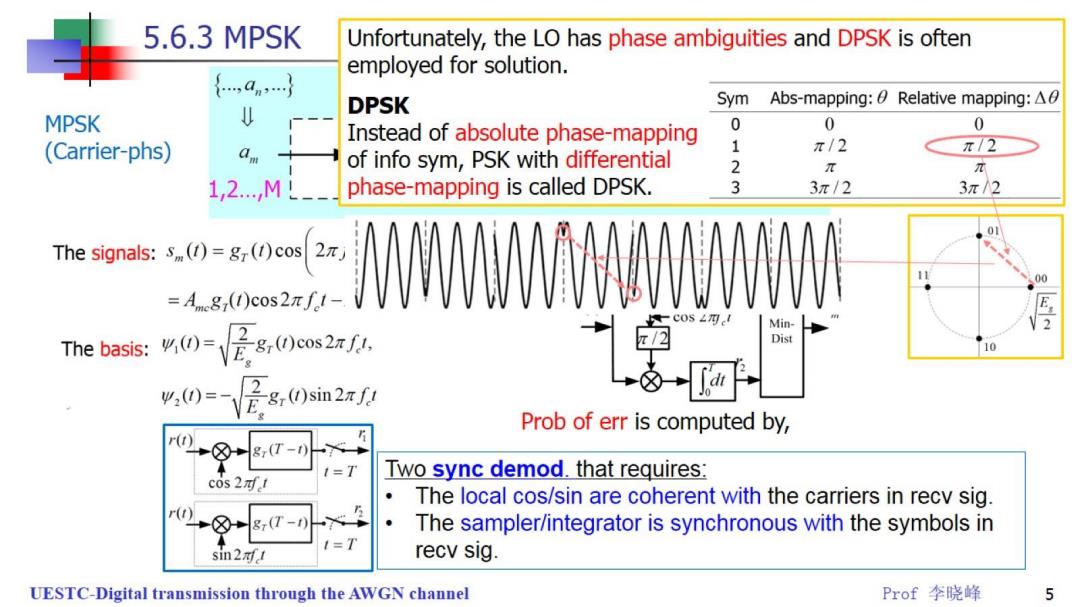
5.6.3 MPSK Unfortunately,the LO has phase ambiguities and DPSK is often employed for solution. DPSK Sym Abs-mapping:Relative mapping:A0 MPSK Instead of absolute phase-mapping 0 0 0 (Carrier-phs) 1 π/2 π72 of info sym,PSK with differential 2 π π 1,2.,ML-- phase-mapping is called DPSK. 3 3m/2 3π/2 0 The signals:s()=gr()cos 00 =Amg(I)cos2πf1 -cos4 Min- 2 %0-28,0cos2 Dist The basis: %0=是,0sm20 Prob of err is computed by, r( →⑧T-0 1=T Two sync demod.that requires: c0s21 The local cos/sin are coherent with the carriers in recv sig. r→⑧8,T-0 The sampler/integrator is synchronous with the symbols in sin2ft recv sig. UESTC-Digital transmission through the AWGN channel Prof李晓峰 5
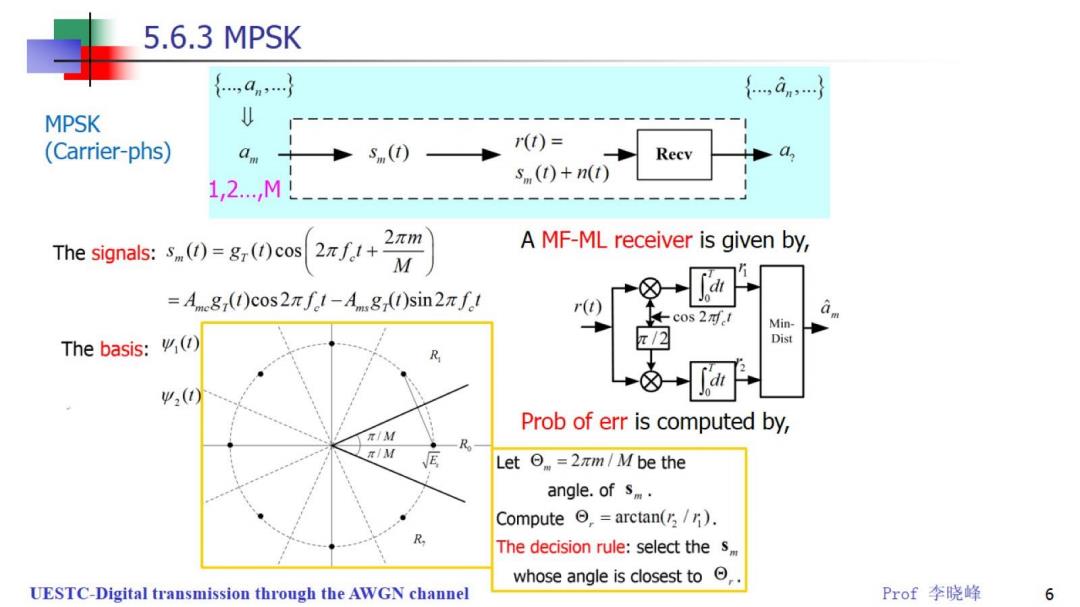
5.6.3 MPSK {,an} {,an,} MPSK (Carrier-phs) s(t) (T)= Recv s (t)+n(t) 1,2.ML The signals:s()=g()cos x+ A MF-ML receiver is given by, =Am8()cos2πf1-Ang()sin2πf1 r(t) ←cos2对I Min- The basis:() Dist () Prob of err is computed by, 元/M π/M E Let=2πm/M be the angle.of s. Compute arctan(/). The decision rule:select the s whose angle is closest to , UESTC-Digital transmission through the AWGN channel Prof李晓峰 6

5.6.3 MPSK {,a} {,an,} MPSK U (Carrier-phs) s(t) (t)= Recv a. s (t)+n(t) 1,2M1 The signals:5()=g(t)cos x+ Prob of err is computed by, =Aueg(t)cos2πf1-Ang()sin2πf1 B=12=1-r The basis:() =1-∫wfe,s)d0 Ψ() For simple cases of M=2 or 4,BPSK and QPSK π/M R πM E P.=0 No R UESTC-Digital transmission through the AWGN channel Prof李晓峰 7
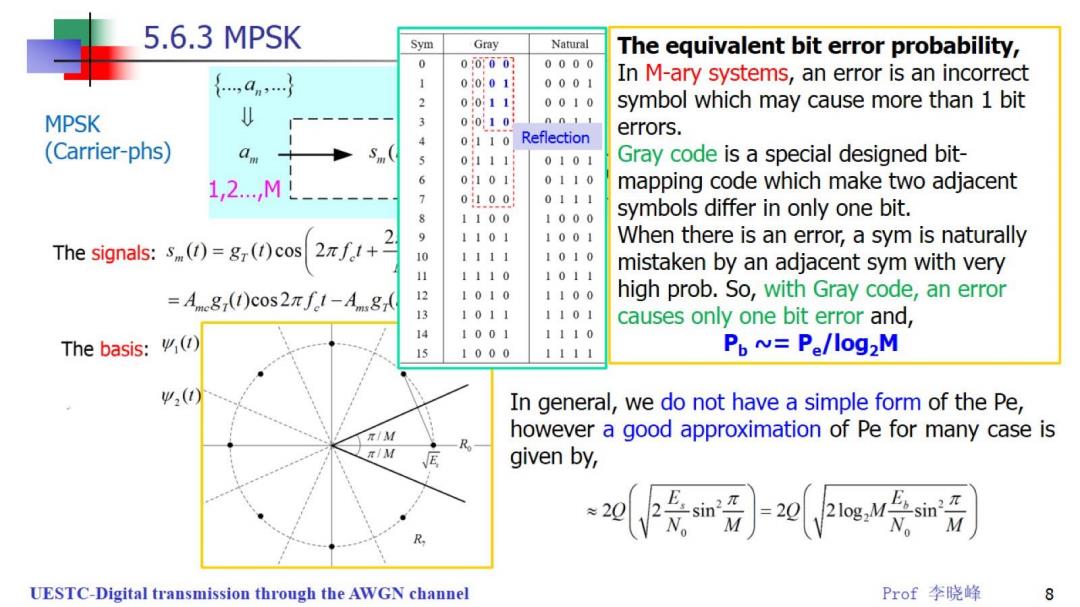
5.6.3 MPSK Sym Gray Natural The equivalent bit error probability, 0 00001 0000 1 0001月 0001 In M-ary systems,an error is an incorrect 2 001 0010 symbol which may cause more than 1 bit MPSK U 3 0010 n011 errors. (Carrier-phs) 0110 Reflection am Sm 5 0111 0101 Gray code is a special designed bit- 1,2…Ml 6 0101 0110 mapping code which make two adjacent 7 01.00 0111 8 1100 1000 symbols differ in only one bit. 2 9 1101 1001 When there is an error,a sym is naturally The signals:s(()=gr()cos 2πf1+ 10 1111 1010 mistaken by an adjacent sym with very 1110 1011 =Ameg(1)cos2f1-Ag( 1 1010 1100 high prob.So,with Gray code,an error 1011 1101 causes only one bit error and, 14 1001 1110 The basis: 1000 Po=Pe/log2M () In general,we do not have a simple form of the Pe, π/M however a good approximation of Pe for many case is π/M E given by, UESTC-Digital transmission through the AWGN channel Prof李晓峰 8

5.6 Binary Baseband: BPAM (antipodal,unipolar),Orthogonal signaling; Passband: BPSK, OOK or BASK, BFSK(Orthogonal) M-ary,1-D signaling Baseband:MPAM Passband: MASK M-ary,2-D signaling (Passband) MPSK, QAM UESTC-Digital transmission through the AWGN channel Prof李晓峰 11

5.6.4QAM {,an} {,an,} QAM (Amp/phs) am s(t) (t)= Recv s (t)+n(t) 1,2.M1 The sionals: 2πm A MF-ML receiver is given by, =Ang()cos2πfc1-Ang()sin2πf61 +⑧面 r() ←cos2对I a Min- The basis:cos2 Dist g0=,0sn2 Prob of err is computed by, UESTC-Digital transmission through the AWGN channel Prof李晓峰 12

5.6.4QAM {人,an} {,an,} QAM (Amp/phs) s (t) r(0)= Recv s (t)+n(t) 1,2M1 The signals: 2πm Prob of err is computed by, The Pe of QAM depends on its specific constellation. =Amcg()cos2πf1-Ang)sin2πfl The distance between pairs of points and the The basis:cos2 average energy are two key paras. %,0=&,0sn2 Rectangular QAM constellations have distinct advantages of being equivalent to 2 PAMs.Though not the best,it is only slightly poorer than the best, so it is frequently used in practical. o.om) UESTC-Digital transmission through the AWGN channel Prof李晓峰 13