
Contents 16 Hrs ■Introduction Geometric rep.of the sig waveforms Pulse amplitude modulation 2-d signal waveforms ■M-d signal waveforms Opt.reception for the sig.in AWGN Optimal receivers and probs of err UESTC-Digital transmission through the AWGN channel Prof李晓峰 2
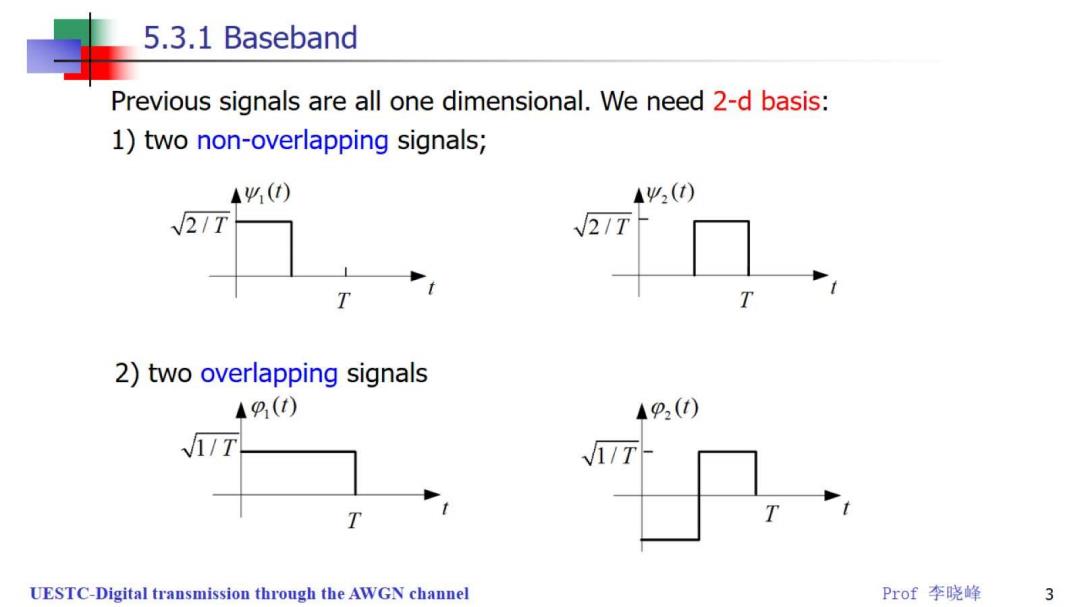
5.3.1 Baseband Previous signals are all one dimensional.We need 2-d basis: 1)two non-overlapping signals; 44() AΨ2(t) √2/T √2/T 2)two overlapping signals 49() 4P() 1/T /1/T- T UESTC-Digital transmission through the AWGN channel Prof李晓峰 3
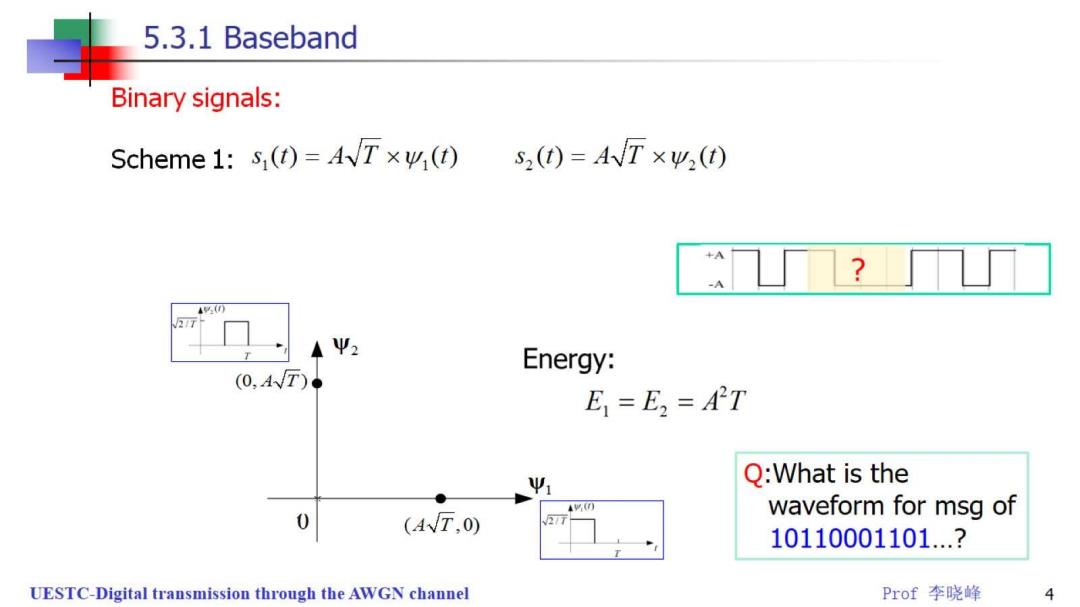
5.3.1 Baseband Binary signals: Scheme 1:s(1)=4Txw (t) S,(0)=AVT×4,(t0 +A ◆Ψ2 Energy: (0,A√T) E=E,=AT Q:What is the 4 (AT,0) waveform for msg of 0 2 10110001101.? UESTC-Digital transmission through the AWGN channel Prof李晓峰 4
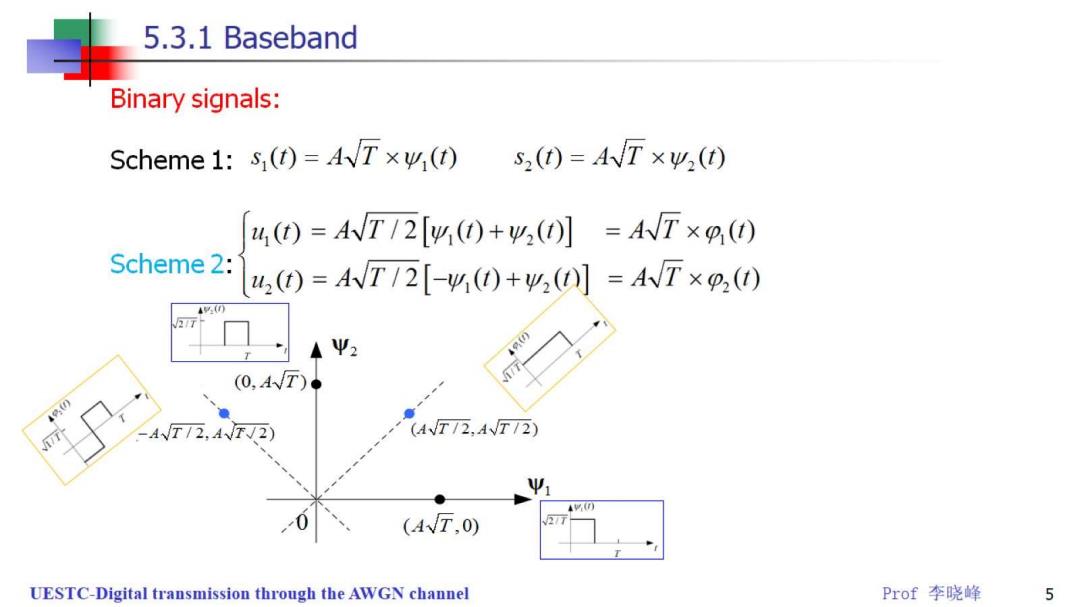
5.3.1 Baseband Binary signals: Scheme 1:s (1)=4Txw(t) S,(0=AVT×4,(t) 4,)=AWT12[4()+4,()】=AWT×m0 Scheme 2: 42(0=AWT12[-4)+4(0]=ANT×p,() 40 Ψ2 (0,4T) 7 AT/2,AT√2) (AJT12,4VT72) Ψ 47 0 (AT,0) 2万 UESTC-Digital transmission through the AWGN channel Prof李晓峰 5

5.3.1 Baseband 4-ary signals 4Ψ s()=a4() s2())=a242(t) Scheme 1: S3(t)=-a4() 0 (AT,0) s4(t)=-a2y2(t) Scheme 2: s()=a1()+a22() S2()=a2141()+a22"2(t) S,()=-[a()+a2y2(] S4(t)=-[a2141(t)+a222(t)] M-ary signals:more to See Fig5.15 and Fig5.16 UESTC-Digital transmission through the AWGN channel Prof李晓峰 6
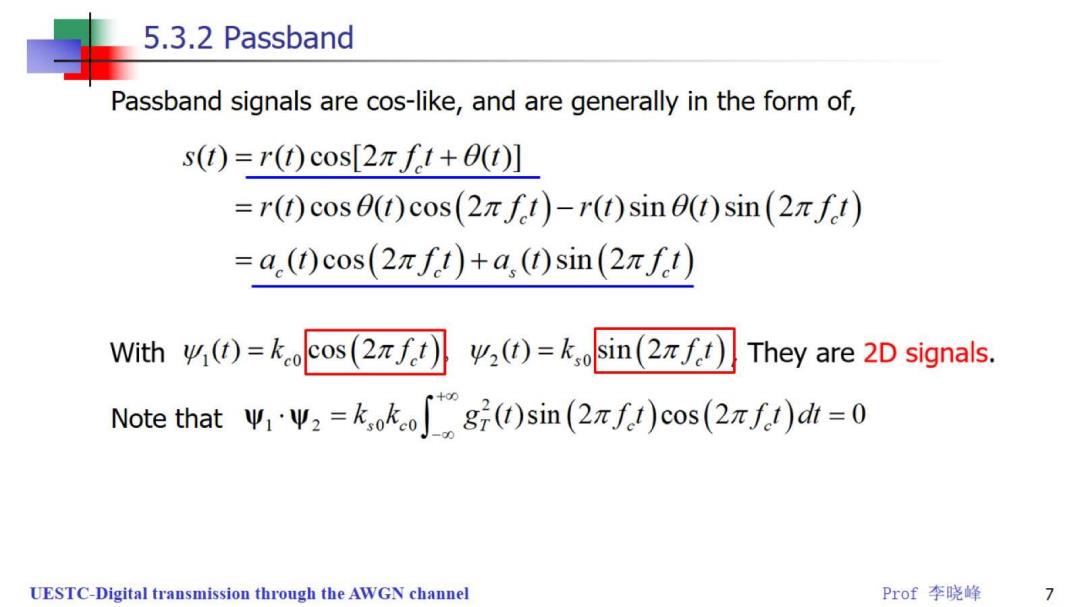
5.3.2 Passband Passband signals are cos-like,and are generally in the form of, s(t)=r()cos[2πft+0t)】] =r(t)cos0(t)cos(27ft)-r(t)sin0(t)sin(2zft) =a.)cos(2πft)+a,()sin(2πft) With y4,0=kocos(2πf) y,)=k,oSin(2πfI】They are2 signals. Note that w1Ψ2=k,okcog7(t)sin(2πft)cos(2πft)dh=0 UESTC-Digital transmission through the AWGN channel Prof李晓峰 7

5.3.2 Passband Carrier-phase modulated signals M.0=8z0c0s2rf1+ 2πm m=0,1,.,M-1 M It is often called PSK(Phase shift keying) Take M=4,QPSK.There are 4 possible phases:0 2πm=0,元/2,元,3元/2 UESTC-Digital transmission through the AWGN channel Prof李晓峰 8

5.3.2 Passband In fact, u(()=g(t)cos 2πf.t+ 2π M =AnegT(t)cos(2πft)-An.g()sin(2πft) Let basis be4())=kgr(t)cos(2πft),y2()=-kg()sin(2πft) Where=/,required by unit basis. Then, un(0=(A,nVE/2)xy4,0+(AneEg/2])×y,0 And the mth signal points,u=(E/2.E/2 UESTC-Digital transmission through the AWGN channel Prof李晓峰 9

5.3.2 Passband Take M=4,QPSK. In fact, um (t)=g(t)cos 2f.1+ 0= πm=0,元/2,元,3r/2, M =A8r(0cos(2πf)u,=(E,/2,0,u=(0,VE12), where,A=cos 〉=m2,=052 2πm Let basis be v(t)=kogr(t)cos(2ft),w2(t)=-k 01 Where=/,required by unit basis. 00 Then, u(=(AmeEg12)xw()+(AneE/2 2 And the mth signal points,u=E/2, 10 UESTC-Digital transmission through the AWGN channel Prof李晓峰 10
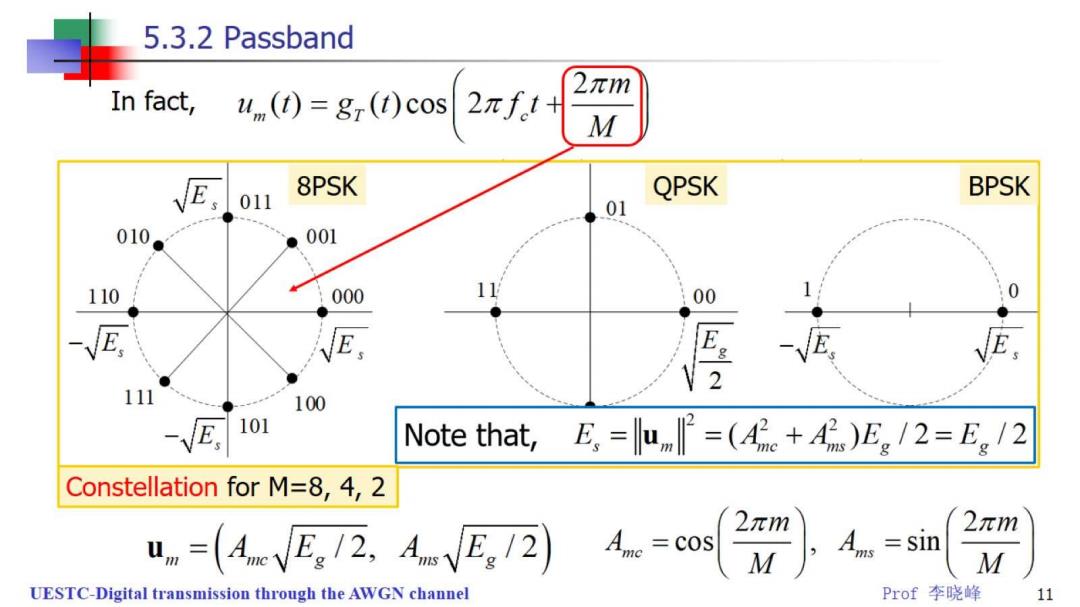
5.3.2 Passband In fact, 2πm um(t)=gr(t)cos2πft+ M E 8PSK QPSK BPSK 011 01 010 ● 001 110 000 00 E 2 111 100 √E 101 Note that,E,=|lumP=(4。+A)E。/2=Eg/2 Constellation for M=8,4,2 2πm 2πm un=(AneEg12,AuE。/2) Ane =cos 4..=sin M UESTC-Digital transmission through the AWGN channel Prof李晓峰 11