西北大学化工原理课件 第二节热传导 一、傅立叶定理及导热系数 1、温度场:某一瞬时固体物体各点的温度情况。通常物体 的温度分布是空间和时间的函数,但 对定态场:1=fx,y,) 对非定态场:t=fx,y,2,T) 2、等温面: 温度场中在同一时刻温度相同的 等温面 各点连起来的面叫等温面。等温面可 以是封闭的,不同的等温面不能相 交,同一等温面上无热量交换,在不 同的温度面上才有热量交换。 t1>t2
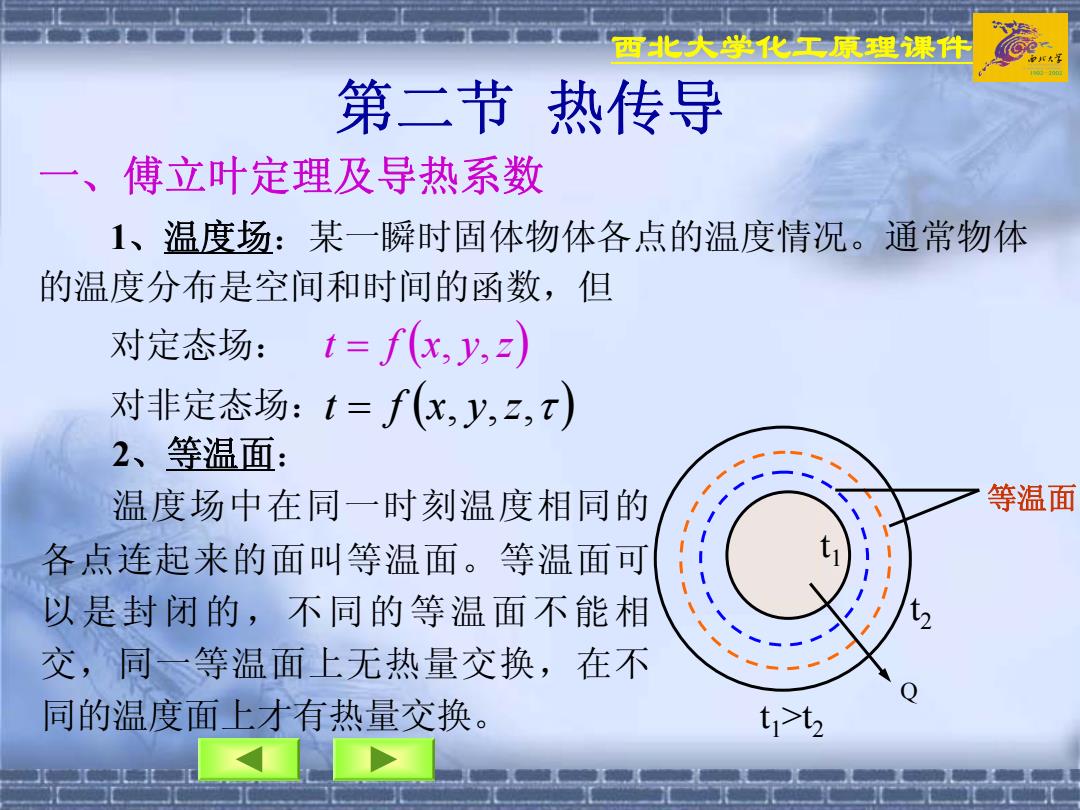
西北大学化工原理课件 第二节 热传导 一、傅立叶定理及导热系数 1、温度场:某一瞬时固体物体各点的温度情况。通常物体 的温度分布是空间和时间的函数,但 对定态场: 对非定态场: t = f (x, y,z) t = f (x, y,z,τ ) 2、等温面: 温度场中在同一时刻温度相同的 各点连起来的面叫等温面。等温面可 以是封闭的,不同的等温面不能相 交,同一等温面上无热量交换,在不 同的温度面上才有热量交换。 t1 t2 t1>t2 等温面 Q

西北大学化工原理课件 △t dt 3、温度梯度: lim t△t n→0 △n dn 温度梯度是向量,其方向垂直于等温面,并 △n 以温度增加的方向为正,其与传热方向相反。 △M 4、傅立叶定律:傅立叶定律是热传导的基 本定律,它指出:单位时间内的热量与温度梯度 温度梯度 及垂直于热流方向的截面积成正比。式中的负号 表明热流方向与温度梯度方向相反。即: Ot 8t O=-九A 或9=-入 On On Ot On 法向温度梯度,°C/m 入 比例系数,称为导热系数,W/m°C 傅立叶定理与牛顿粘性定理很相似
西北大学化工原理课件 3、温度梯度: 温度梯度是向量,其方向垂直于等温面,并 以温度增加的方向为正,其与传热方向相反。 4、傅立叶定律 :傅立叶定律是热传导的基 本定律,它指出:单位时间内的热量与温度梯度 及垂直于热流方向的截面积成正比。式中的负号 表明热流方向与温度梯度方向相反。即:t q n λ ∂ = − ∂ t Q A n λ ∂ = − ∂ dn dt n t n = Δ Δ Δ → lim 0 或 n t ∂ ∂ C / m D ——法向温度梯度, λ W m CD ——比例系数,称为导热系数, / ⋅ 傅立叶定理与牛顿粘性定理很相似。 t+ t t Δn Δl 温度梯度 Δ Q

西北大学化工原理课件 5、导热系数 国际上J1msC)(W1mC 工程上 kcallm-h~C) 从傅立叶定律知:入=一 Ot A. On 此即为导热系数的定义式,表示单位导热面积、单位温度 梯度,在单位时间内传导的热量。 所以入是表征物质导热能力的一个参数,为物质物性之一。 其值与物质的组成结构和状态等参数有关,入越大,导热越快。 它也是分子微观运动的宏观表现。通常用实验方法测定
西北大学化工原理课件 此即为导热系数的定义式,表示单位导热面积、单位温度 梯度,在单位时间内传导的热量。 国际上 工程上 (J m s C) D λ / ⋅ ⋅ (W m C) D / ⋅ (kcal m h C) D / ⋅ ⋅ Q t A n λ = − ∂ ⋅ ∂ 从傅立叶定律知: 所以λ是表征物质导热能力的一个参数,为物质物性之一。 其值与物质的组成结构和状态等参数有关,λ越大,导热越快。 它也是分子微观运动的宏观表现。通常用实验方法测定。 5、导热系数

西北大学化工原理课件 e= 一 般有: 九個>九液>九 九金>九年 入固随温度而变,绝大多数质地均匀的固体,导热系数与温度 近似成线性关系。即:九=2,(1+ot) 入0— 固体在t℃时的导热系数。 温度系数,K。对金属0=负值;对非金属0=正值。 P175图6-4与图65列了一些导热系数。 物质种类 金属 非金属固体 液体 气体 绝热材料 入,W/mK10~500 0.1~10 0.05~1.0 0.005~0.5 <0.25
西北大学化工原理课件 λ固随温度而变,绝大多数质地均匀的固体,导热系数与温度 近似成线性关系。即: λ固 > λ液 > λ气 λ金 > λ非 λ0——固体在t℃时的导热系数。 α ——温度系数, 。对金属 K−1 α=负值;对非金属α=正值。 P175图6-4与图6-5列了一些导热系数。 一般有: (1 ) 0 λ = λ +αt λ,W/(m⋅K) 10~500 0.1~10 0.05~1.0 0.005~0.5 <0.25 物质种类 金属 非金属固体 液体 气体 绝热材料
西北大学化工原理课件 二、平壁的定态热传导 1、单层平壁的热传导 (1)平壁内的温度分布 t 如图所示为一平壁,其厚为δ。 单层的条件:A、等温面为垂直 于x轴的平行平面。(一维单向热传导) B、设壁的材质均匀:2≠f) C、定态导热t=fx,y,2 平壁的两侧面的温度t及t,恒定。 x+dx 当x=0时,t1;当x=δ时,。t2。 根据傅立叶定律:g=-入 X on 在平壁内部取厚度为△x的薄层,对比薄层取单位面积作热 量衡算,可得
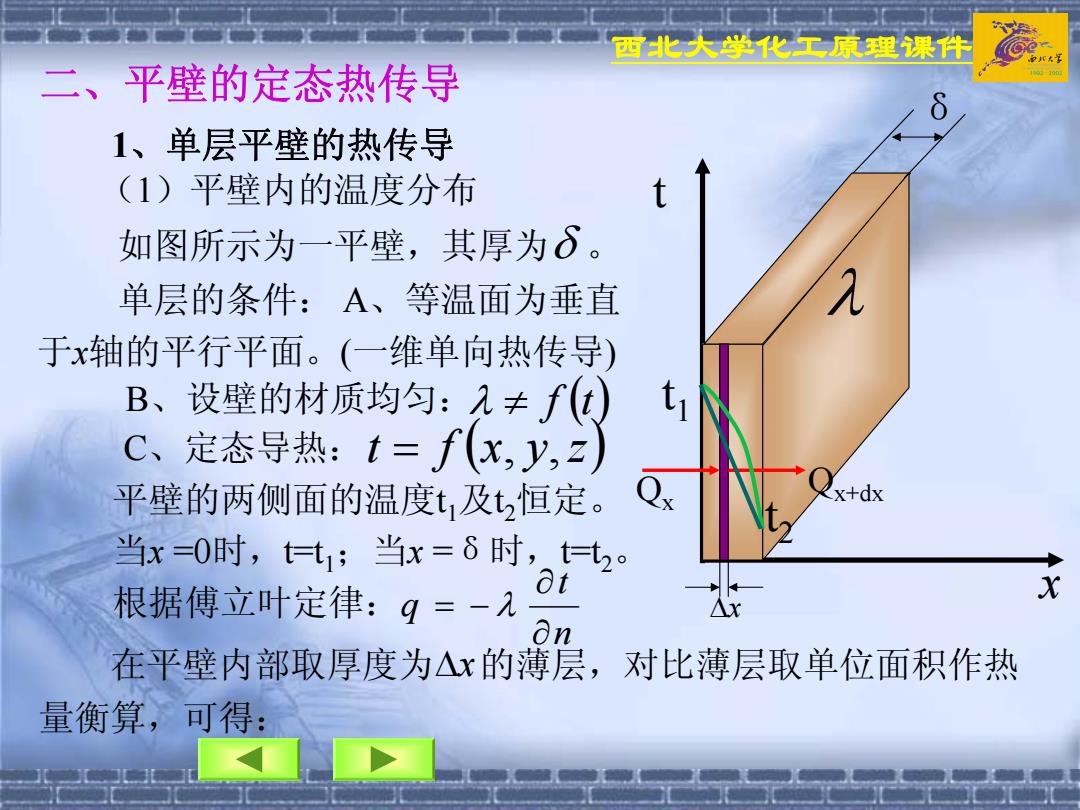
西北大学化工原理课件 在平壁内部取厚度为 的薄层,对比薄层取单位面积作热 量衡算,可得: 二、平壁的定态热传导 1、单层平壁的热传导 (1)平壁内的温度分布 如图所示为一平壁,其厚为 。 单层的条件: A、等温面为垂直 于x轴的平行平面。(一维单向热传导) 平壁的两侧面的温度t1及t2恒定。 当x =0时,t=t1;当x =δ时,t=t2。 根据傅立叶定律: λ ≠ f (t) t = f (x, y,z) δ Δx n t q ∂ ∂ = − λ dx B、设壁的材质均匀: C、定态导热: t1 t2 δ λ t x Qx Qx+dx Δx

西北大学化工原理课件 q,=qls+AxpCp Ot Ot 对定态导热: =0 Or 薄层内无热量累积: ql glstas 上式化为:q=-元=常数 dx 当2=const时, dt=常量, 即平壁内温度呈直线分布。 dx 当入随t变化时,温度分布呈曲线,入随上升而增大时, 曲线位于直线上方;入随t减小时,温度分布曲线位于直线的 下方。一般的入取平均值
西北大学化工原理课件 当λ随t 变化时,温度分布呈曲线,λ随t上升而增大时, 曲线位于直线上方;λ随t 减小时,温度分布曲线位于直线的 下方。 一般的λ取平均值。 x xx p t q q xCρ τ +Δ ∂ = +Δ ∂ = 0 ∂ ∂ τ t x xx q q + Δ = = − = 常数 dxdt q λ 当 时 λ = const , = 常量,即平壁内温度呈直线分布。 dxdt 对定态导热: 薄层内无热量累积: 上式化为:

西北大学化工原理课件 (2)热流量 对上面定态导热,q不随x变化,积分9=一本得: dt us q=g=1五=元 A (6-9) X2-X1 A(4-t2) △t △t 推动力 (6-10) 8 6 R 阻力 几A 8 即:R= 九A
西北大学化工原理课件 (2)热流量 对上面定态导热,q不随x变化,积分 ,得: dx x q x dt t t ∫ ∫ = − 1 2 1 2 λ 1 2 2 1 Q t t t q A xx λ λ δ − Δ == = − At t ( ) 1 2 t t Q R A λ δ δ λ − Δ Δ = = == 推动力 阻力 R A δ λ = dx dt q = −λ (6-10) (6-9) 即:

西北大学化工原理课件 Ge- 上式表明:Q正比于△t,反比于R,这与欧姆定律 极为类似,且δ越大,A和几越小,R就越大。 可以证明,若将入与t的关系近似地用线性方程式: 2=,(1+0t)表示,则式(6-9)、(6-10)仍适用, 只是式中的导热系数应以平均值代替: + 2 入m就是当温度t=(化,+12)时的导热系数。 2
西北大学化工原理课件 上式表明 :Q正比于 ,反比于 R,这与欧姆定律 极为类似,且 越大,A 和 越小,R 就越大。 Δt δ λ 可以证明,若将 与 t 的关系近似地用线性方程式: 表示,则式(6-9)、(6-10)仍适用 , 只是式中的导热系数应以平均值代替: λ 0 λ = + λ α (1 )t 2 λ1 λ2 λ + m = ( ) 21 1 2 t = t + t λ m就是当温度 时的 导热系数

西北大学化工原理课件 ©e 2、多层平壁的定态导热过程 我们以三层平壁为例来说明多层导热过程的计算。 t 三层条件: A、各层材质均匀,几1,几2,乙为常数: B、层与层之间接触良好,相互接触的 表面上温度相等; C、各等温面皆为垂直于x轴的平行平 面,壁的面积为A,在定态导热过 x 程中,穿过各层的热量必相等。 (没有热量积累)
西北大学化工原理课件 2、多层平壁的定态导热过程 我们以三层平壁为例来说明多层导热过程的计算。 x t 1t 2t 3t 4t ← ⎯→ ⎯→1 ← ⎯→ ← δλ1 λ2 λ3 δ 2 δ 3 三层条件: A、各层材质均匀, 为常数; B、层与层之间接触良好,相互接触的 表面上温度相等; C、各等温面皆为垂直于x轴的平行平 面,壁的面积为A,在定态导热过 程中,穿过各层的热量必相等。 ( 没有热量积累) 1 2 3 λ ,λ ,λ
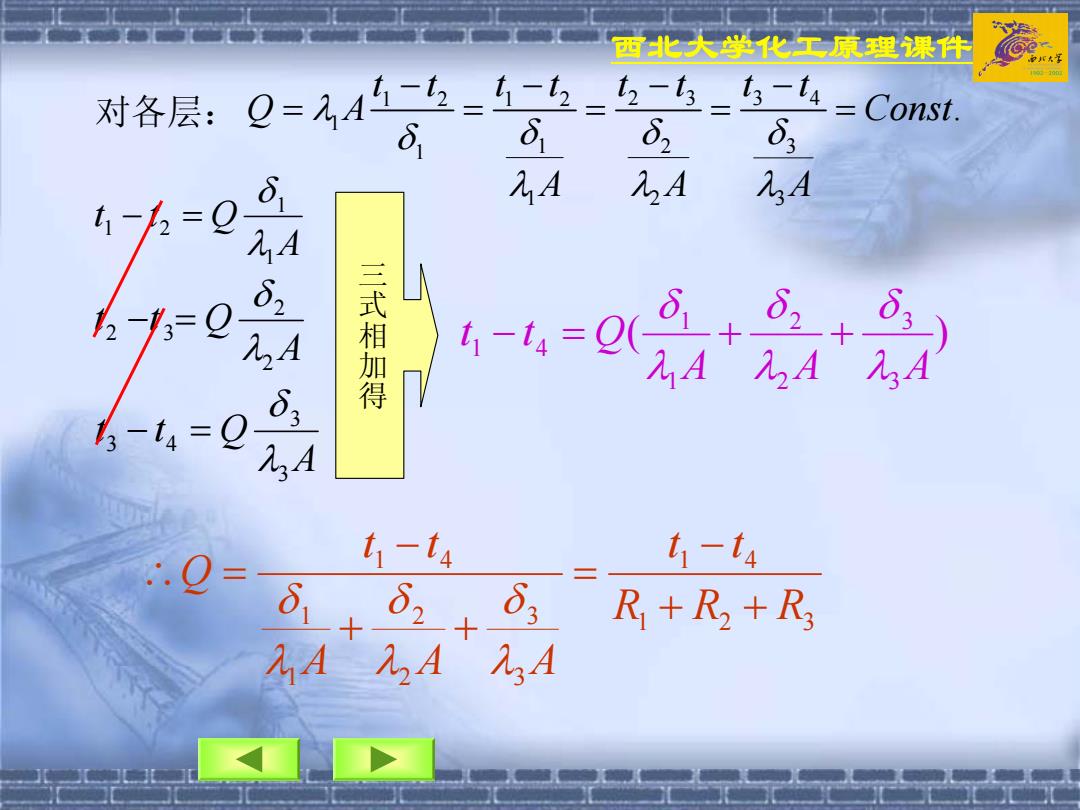
西北大学化工原理课件 对各层:Q=4二飞=-4- t2-t3_43-t4 可 62 可3 =Const. 61 元A LA LA A = δ2 三式相加得 --0 d2+ -t4=0 ,A t1-t4 t1-t4 0+02+0 R+R2+R3 1A几A'八3A
西北大学化工原理课件 对各层: 12 12 23 34 1 1 123 1 2 3 . tt tt tt tt Q A Const A A A λ δ δδδ λ λ λ − − − − = ==== A t t Q 1 1 1 2 λ δ − = A t t Q 2 2 2 3 λ δ − = A t t Q 3 3 3 4 λ δ − = 三式相加得 ( ) 3 3 2 2 1 1 1 4 A A A t t Q λ δ λ δ λ δ − = + + 1 2 3 1 4 3 3 2 2 1 1 1 4 R R R t t A A A t t Q + + − = + + − ∴ = λ δ λ δ λ δ