中国石油大学（华东）：《化工热力学》课程教学资源（课件讲义）第4章 溶液热力学性质计算

第4章 溶液热力学性质的计算 气态溶液 固态溶液 液态溶液 广义地说，两种或两种以上物 质彼此以分子或离子状态均匀 混合所形成的体系称为溶液 溶液 (solution)或者混合物。 >在工程上的应用十分广泛。 电解质溶液 *非电解质溶液 >本章特点：概念多、公式推 导多 均相多元体系，本章溶液一般指 气体混合物和液体混合物。 惟真帷竇

溶 液 气态溶液 固态溶液 液态溶液 电解质溶液 非电解质溶液 广义地说，两种或两种以上物 质彼此以分子或离子状态均匀 混合所形成的体系称为溶液 (solution)或者混合物。 在工程上的应用十分广泛。 本章特点：概念多、公式推 导多 均相多元体系，本章溶液一般指 气体混合物和液体混合物。 第4章 溶液热力学性质的计算

第4章 溶液热力学性质的计算 4.1均相敝开系统的热力学基本关系 4.2偏摩尔性质 4.3混合变量 4.4逸度和逸度系数 4.5理想溶液和非理想溶液 4.6活度及活度系数 4.7超额性质 4.8活度系数模型 惟真帷竇

4.1 均相敞开系统的热力学基本关系 4.2 偏摩尔性质 4.3 混合变量 4.4 逸度和逸度系数 4.5 理想溶液和非理想溶液 4.6 活度及活度系数 4.7 超额性质 4.8 活度系数模型 第4章 溶液热力学性质的计算

4.1均相敞开系统的热力学基本关系 一变组成体系热力学性质间的关系式 对多组分体系的单相敞开系统，体系的性质与物质的量（摩 尔数)有关，如体系的Gibbs自由能 G=nG=GT,D,n1L.·,N) G的全微分： dn; aG3ar++2C dn; T.p.nje 惟真帷竇

4.1 均相敞开系统的热力学基本关系 —变组成体系热力学性质间的关系式 对多组分体系的单相敞开系统，体系的性质与物质的量（摩 尔数）有关，如体系的Gibbs自由能 Gt=nG = G(T , p , n1 , n2 ,. . . ,nN ) Gt的全微分：                                  i i p n T n i T p n n n G p p G T T G G j i d d d d , , t , t , t t =-St = Vt                 N i i i T p n n n G G S T V p j i 1 , , t d t t d t d d

dG,=-SdT+Vdp on:) dn; T,p,njti dU,TdS,-pdV+ dni 均相敞开体系的热 SVnjei 力学基本关系式。 dH,TdS,+Vdp+ H 当n,全部保持不变 dni on (dn=0)时，就简化 Stp,njti 成定组成体系的基 N d4=-8a7-p+ dni 本热力学关系式。 惟真帷實

                N i i i T p n n n G G S T V p j i 1 , , t d t t d t d d                N i i i S V n n n U U T S p V j i 1 , , t d t d t d t d t t                N i i i S p n n n H H T S V p j i 1 , , t d t d t t d d t                 N i i i T V n n n A A S T p V j i 1 , , t d t t d d t d t 均相敞开体系的热 力学基本关系式。 当ni全部保持不变 (dni =0)时，就简化 成定组成体系的基 本热力学关系式

化学位， 即 1是状态函数，强 度性质； aU, H, Oni 2.化学位总是指某 SVj Oni Stpnjti 种物质的化学位； 3.不同物质的化学位 a T,p,njti 不能作比较； 4表示物质的逃逸 式中下标n是指除组分外其余所有组 倾向和相变化或化 分的量都保持不变。 学变化的推动力。 惟真帷竇

化学位μi，即 , , t , , t , , t , , t t t t t j i j i j i j i i T V n i T p n i S V n i S p n i n G n A n H n U                                                  式中下标nj≠i是指除i组分外其余所有组 分的量都保持不变。 1.μi是状态函数，强 度性质； 2. 化学位总是指某 种物质的化学位； 3.不同物质的化学位 不能作比较； 4.μi表示物质的逃逸 倾向和相变化或化 学变化的推动力

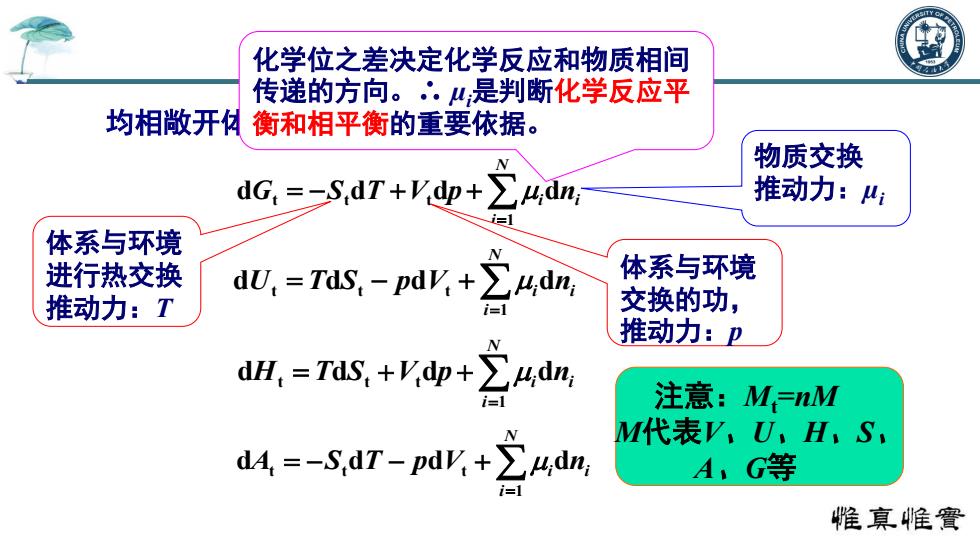
化学位之差决定化学反应和物质相间 传递的方向。∴.是判断化学反应平 均相敞开 】衡和相平衡的重要依据。 物质交换 dG.=二s,dT+yy+∑4dm, 推动力： 体系与环境 进行热交换 dU,=Tis,-p阳K+24n 体系与环境 推动力：T i=1 交换的功， dH,=Tis,+g+之4dn 推动力：卫 注意：M=nM M代表V.U,H,S, dd=-SdT-pdV.+>udn A,G等 惟真帷實

均相敞开体系的热力学基本性质关系式：      N i G S T V p i ni 1 d t t d t d  d     N i U T S p V i ni 1 d t d t d t  d     N i H T S V p i ni 1 d t d t t d  d      N i A S T p V i ni 1 d t t d d t  d 注意：Mt=nM M代表V、U、H、S、 A、G等 体系与环境 进行热交换 推动力：T 体系与环境 交换的功， 推动力：p 物质交换 推动力：µi 化学位之差决定化学反应和物质相间 传递的方向。∴ µi是判断化学反应平 衡和相平衡的重要依据

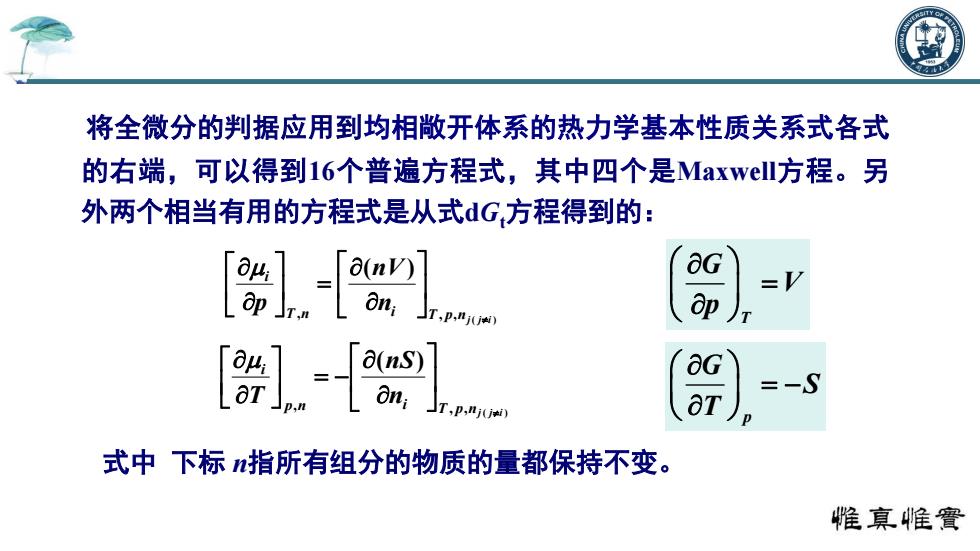
将全微分的判据应用到均相敝开体系的热力学基本性质关系式各式 的右端，可以得到16个普遍方程式，其中四个是Maxwell7方程。另 外两个相当有用的方程式是从式dG方程得到的： aG =V ap =-S T,p,nj(jti) OT) 式中下标指所有组分的物质的量都保持不变。 惟真帷竇

将全微分的判据应用到均相敞开体系的热力学基本性质关系式各式 的右端，可以得到16个普遍方程式，其中四个是Maxwell方程。另 外两个相当有用的方程式是从式dGt方程得到的： 式中 下标 n指所有组分的物质的量都保持不变。 ( ) , , , ( ) T p nj j i T n i i n nV p                   ( ) , , , ( ) T p nj j i p n i i n nS T                    T G V p          p G S T          

第4章 溶液热力学性质的计算 4.1均相敞开系统的热力学基本关系 4.2偏摩尔性质 4.3混合变量 4.4逸度和逸度系数 4.5理想溶液和非理想溶液 4.6活度及活度系数 4.7超额性质 4.8活度系数模型 惟真帷實

4.1 均相敞开系统的热力学基本关系 4.2 偏摩尔性质 4.3 混合变量 4.4 逸度和逸度系数 4.5 理想溶液和非理想溶液 4.6 活度及活度系数 4.7 超额性质 4.8 活度系数模型 第4章 溶液热力学性质的计算

4.2偏摩尔性质 对溶液，热力学性质不仅和温度、压力等有关，而且与体 系的组成有关。 ◆以体系的总体积为例来说明 ~对理想的混合物，其总体积 V >但对一般的真实体系 V 惟真帷竇

 对溶液，热力学性质不仅和温度、压力等有关，而且与体 系的组成有关。  以体系的总体积为例来说明  对理想的混合物，其总体积  但对一般的真实体系 4.2 偏摩尔性质   N i V ni Vi 1 t   N i V ni Vi 1 t

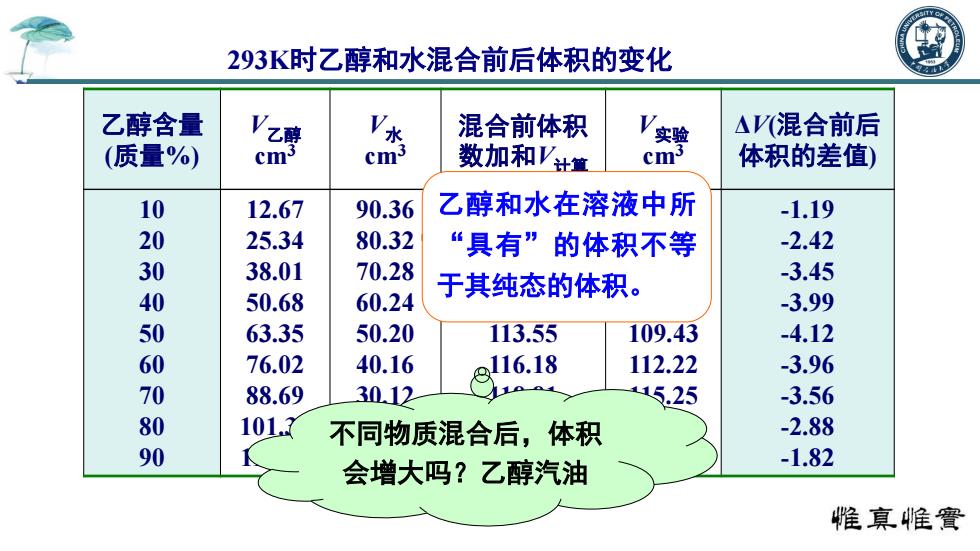
293K时乙醇和水混合前后体积的变化 乙醇含量 Vz 混合前体积 实验 △V(混合前后 (质量%) cm' cm3 数加和Vt童 cm 体积的差值) 10 12.67 90.36 乙醇和水在溶液中所 -1.19 20 25.34 80.32 “具有”的体积不等 -2.42 30 38.01 70.28 60.24 于其纯态的体积。 -3.45 40 50.68 -3.99 50 63.35 50.20 113.55 109.43 -4.12 60 76.02 40.16 116.18 112.22 -3.96 70 88.69 3012 5.25 -3.56 80 101 不同物质混合后，体积 -2.88 90 会增大吗？乙醇汽油 -1.82 惟真帷實

乙醇含量 (质量%) V乙醇 cm3 V水 cm3 混合前体积 数加和V计算 V实验 cm3 ΔV(混合前后 体积的差值) 10 20 30 40 50 60 70 80 90 12.67 25.34 38.01 50.68 63.35 76.02 88.69 101.36 114.03 90.36 80.32 70.28 60.24 50.20 40.16 30.12 20.08 10.04 103.03 105.66 108.29 110.92 113.55 116.18 118.81 121.44 124.07 101.84 103.24 104.84 106.93 109.43 112.22 115.25 118.56 122.25 -1.19 -2.42 -3.45 -3.99 -4.12 -3.96 -3.56 -2.88 -1.82 乙醇和水在溶液中所 “具有”的体积不等 于其纯态的体积。 不同物质混合后，体积 会增大吗？乙醇汽油 293K时乙醇和水混合前后体积的变化