
>相是指体系中的一个均匀空间部分,其性质和其余部 蒸 分有区别。 相迁移过程:物质从一相迁移到另一相的过程 液体 >从宏观上看,当物质相迁移和能量交换都停止时,每 个相的性质和组成不再随时间而变化,即处于相平衡。 >相平衡是一种动态平衡。 糇真帷竇
相是指体系中的一个均匀空间部分,其性质和其余部 分有区别。 相迁移过程:物质从一相迁移到另一相的过程 从宏观上看,当物质相迁移和能量交换都停止时,每 个相的性质和组成不再随时间而变化,即处于相平衡。 相平衡是一种动态平衡。 蒸汽 液体 i
肺动脉 肺静脉 →表示C0,扩散 →表示0,扩散 肺泡外毛细血管 水吸引肥皂 群肥皂分子 分子的头部 肥皂分子的尾部 离开油脂 被油脂吸引 油脂 衣物 衣物 生活中很多事情都涉及相转移问题 惟真帷實
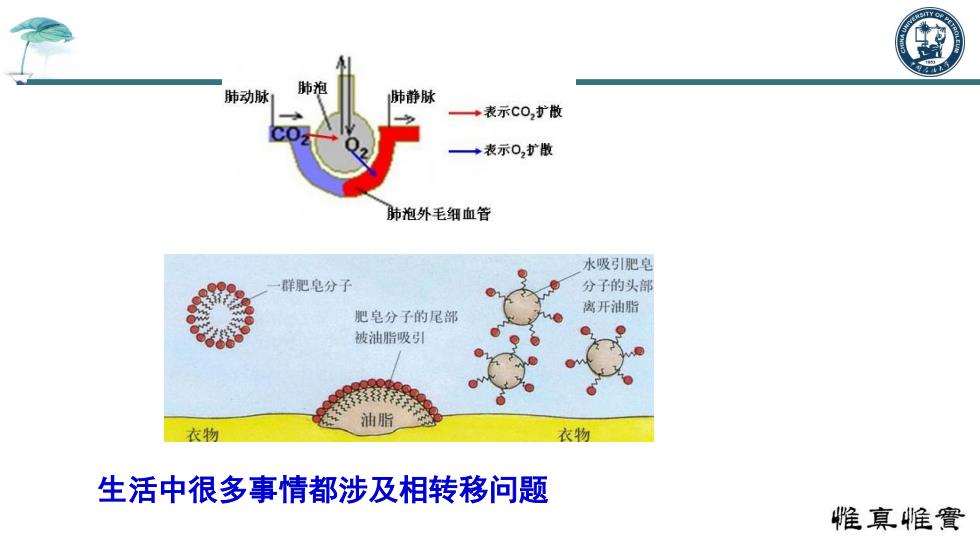
生活中很多事情都涉及相转移问题
A和B 进一步参加反应 提纯 反应物 原 A 产物 含A、B、 分离 纯C 产品 + 料 C、D、E 反应物 的混合物 提纯 B D和E 副产品 惟真帷竇
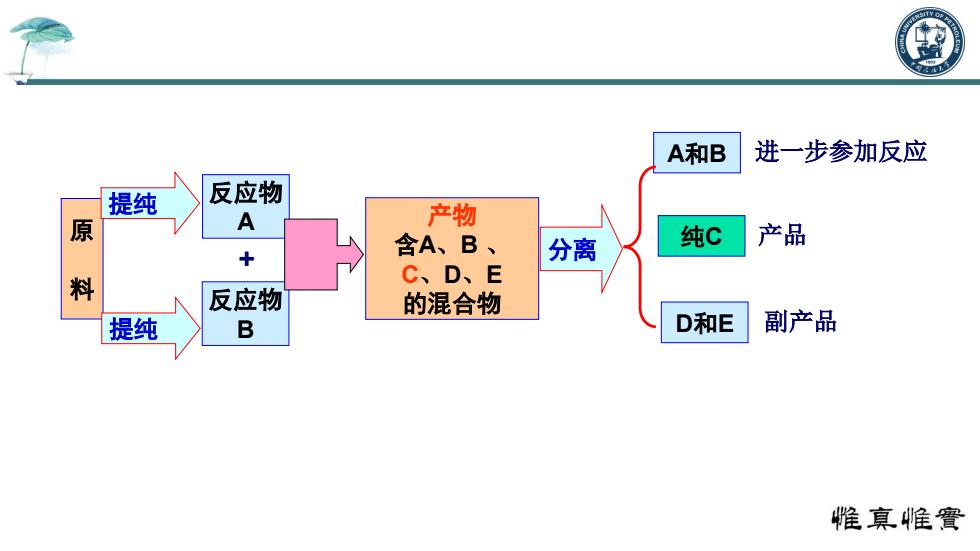
反应物A 反应物B+ 产物 含 A 、B 、 C 、 D 、 E 的混合物 A 和 B 纯 C D 和 E 进一步参加反应 产品 副产品 分离 原料 提纯 提纯
典型的分离操作:精馏、吸收、萃取、结晶等 精缩装置示意图 相平衡热力学是一切分离技术及分离设备开发、设计 的理论基础。 惟真帷竇
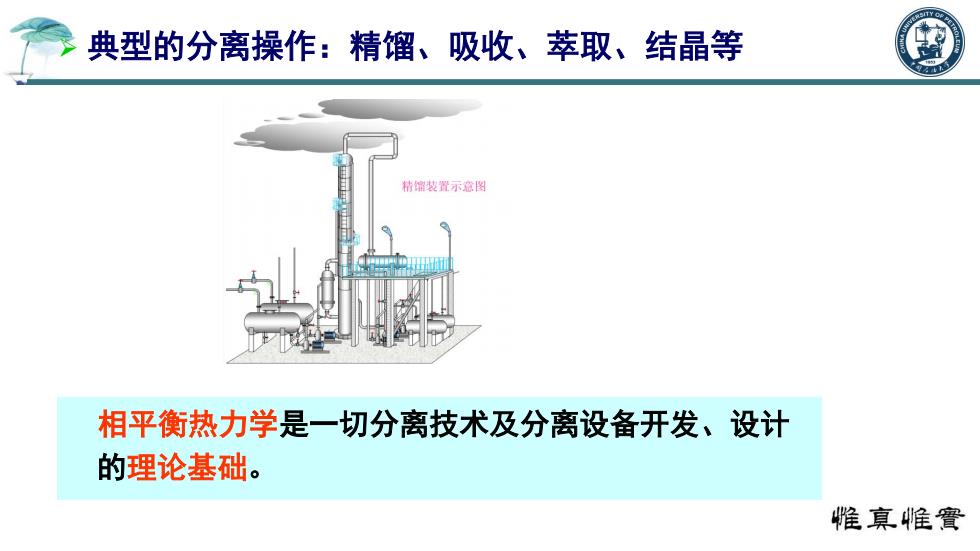
典型的分离操作:精馏、吸收、萃取、结晶等 相平衡热力学是一切分离技术及分离设备开发、设计 的理论基础

1相平衡的判据 平衡判据的确定应以热力学第二定律为依据。 熵增原理: 即 (dS)s≥0或dSu20 这是普遍适用的判据。 惟真帷竇
1 相平衡的判据 平衡判据的确定应以热力学第二定律为依据。 熵增原理: 即 (dS)iso≥ 0 或 dSU,V≥0 这是普遍适用的判据

dSv.r20 达平衡时 Siso→mx + dUs≤0 达平衡时 Usyst→min dHp.s≤0 达平衡时Hyst→min dAz≤0 达平衡时 Asyst→min ★dGrp≤0 达平衡时 Gsyst→nin 在相平衡和化学平衡中采用Gibbs自由能的平衡判据应 用最为广泛。 惟真帷實
dSU,V≥0 达平衡时 Siso→ max dUS,V≤0 达平衡时 Usyst→ min dHp,S≤0 达平衡时 Hsyst→ min dAT,V≤0 达平衡时 Asyst→ min dGT,p≤0 达平衡时 Gsyst→ min 在相平衡和化学平衡中采用Gibbs自由能的平衡判据应 用最为广泛

恒温恒压下的封闭体系,平衡的判据可表达为 (dG)z.p-0 () 根据式(1),可推出相平衡的条件为: “各相的温度相等、压力相等、各组分在各相的化学位相等” Ta=T邢==Tm p=p=.=p π个相,N个组分 =1,2,.,N 4==.=4 惟真帷竇
恒温恒压下的封闭体系,平衡的判据可表达为 (dG)T,p =0 (1) 根据式(1),可推出相平衡的条件为: “各相的温度相等、压力相等、各组分在各相的化学位相等” α β π μi i i μ μ π个相,N个组分 i=1,2,.,N α β π T T T α β π p p p

将(1)式应用于一个多组分两相(相与β相)平衡的封闭体 系。 体系Gibbs自由能的变化: d(nG)=d(nG)“+d(nG)P 由单相敞开体系的热力学关系式: d(nG)=-(nS)dT+(nV)dp+>udn; 体系与环境 体系与环境 物质交换 进行热交换 交换的功, 推动力:T 推动力: 推动力:卫 惟真帷實
将(1)式应用于一个多组分两相(α相与β相)平衡的封闭体 系。 体系Gibbs自由能的变化: 由单相敞开体系的热力学关系式: i ni d(nG) (nS)dT (nV)dp d i α β 体系与环境 进行热交换 推动力:T 体系与环境 交换的功, 推动力:p 物质交换 推动力:µi α β d( ) d( ) d( ) nG nG nG

在恒温恒压下(dT=0,dp=0),则 对相:d(nG)°=∑4dm 对相:d(nG)P=∑4dm d(nG)=∑dm+∑4dn 如果体系在恒温恒压下两相达平衡状态,则 d(nG)=0 惟真帷竇
在恒温恒压下(dT=0,dp=0),则 对α相: 对β相: ∴ 如果体系在恒温恒压下两相达平衡状态,则 d(nG)=0 α α α d( ) d nG n i i β β β d( ) d nG n i i α α β β d( ) d d nG n n i i i i
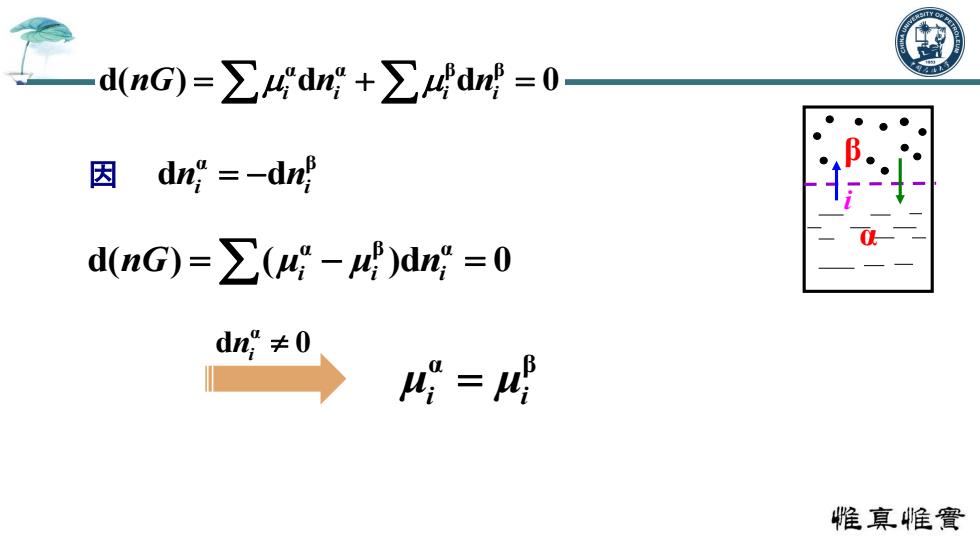
d(nG)=∑4dn+∑4dr=0 因dn=-dn d(nG)=∑(-4)dn=0 dn≠0 4=4 惟真帷實
因 i α β α β α d( ) ( )d 0 nG μi i i μ n α d 0 ni α β d d n n i i α α β β d( ) d d 0 nG n n i i i i α β μi i μ