
引言 ◆动力循环一正向循环 液态水 ◆制冷循环一逆向循环 加热 ◆蒸汽动力循环是目前最广泛的获取电能的方式;制冷循环, 可使冰箱、空调为我们所用。 ◆化工生产:动力驱动、制冷降温 ◆循环本质:功与热之间的相互转化。 ◆能量的转化:借助工质在循环过程中连续不断、周而复始 的发生-T变化,状态变化过程中将热转化为功。 ◆工质的膨张和压缩构成了这两类循环的基本元素。 惟真帷竇
引 言 动力循环—正向循环 制冷循环—逆向循环 蒸汽动力循环是目前最广泛的获取电能的方式;制冷循环, 可使冰箱、空调为我们所用。 化工生产:动力驱动、制冷降温 循环本质:功与热之间的相互转化。 能量的转化:借助工质在循环过程中连续不断、周而复始 的发生p-T-V变化,状态变化过程中将热转化为功。 工质的膨胀和压缩构成了这两类循环的基本元素

第7章 压缩、膨胀、动力循环与制冷循环 7.1气体的压缩 7.2气体的膨胀 7.3蒸汽动力循环 7.4制冷循环 惟真帷竇
7.1 气体的压缩 7.2 气体的膨胀 7.3 蒸汽动力循环 7.4 制冷循环 第7章 压缩、膨胀、动力循环与制冷循环
7.1气体的压缩 压气机:鼓风机、压缩机等 特点:消耗能量-电能或机械能 按压缩机运动机构来分 W-1/30 〔往复式(活塞式) 空气压缩机 叶轮式:离心式、轴流式 7.1.1活塞式压气机的压气过程 活 活塞往复运动 塞 吸气压缩 排气 图7-2活塞式压气机的理想 过程 惟真帷竇
7.1 气体的压缩 压气机:鼓风机、压缩机等 特点:消耗能量-电能或机械能 按压缩机运动机构来分 往复式(活塞式) 叶轮式:离心式、轴流式 7.1.1 活塞式压气机的压气过程 活塞往复运动 吸气 压缩 排气 空气压缩机 图7-2 活塞式压气机的理想 过程

7.1气体的压缩 2 7.1.2压缩过程的热力学分析 按理想气体的可逆过程。 气体的压缩过程可视为稳流过程。 则能平式(忽略动、位能变化) 图7-4压缩过程的T-S图 △H=Q+W 卫2 2r 2m2s 对可逆过程,其轴功 形ew=∫W 图7-3压缩过程的p-V图帷竇
7.1 气体的压缩 7.1.2 压缩过程的热力学分析 按理想气体的可逆过程。 气体的压缩过程可视为稳流过程。 则能平式(忽略动、位能变化) 对可逆过程,其轴功 图7-3 压缩过程的p -V 图 图7-4 压缩过程的T -S 图 ΔH = Q +Ws ∫ = 2 1 s,rev d p p W V p
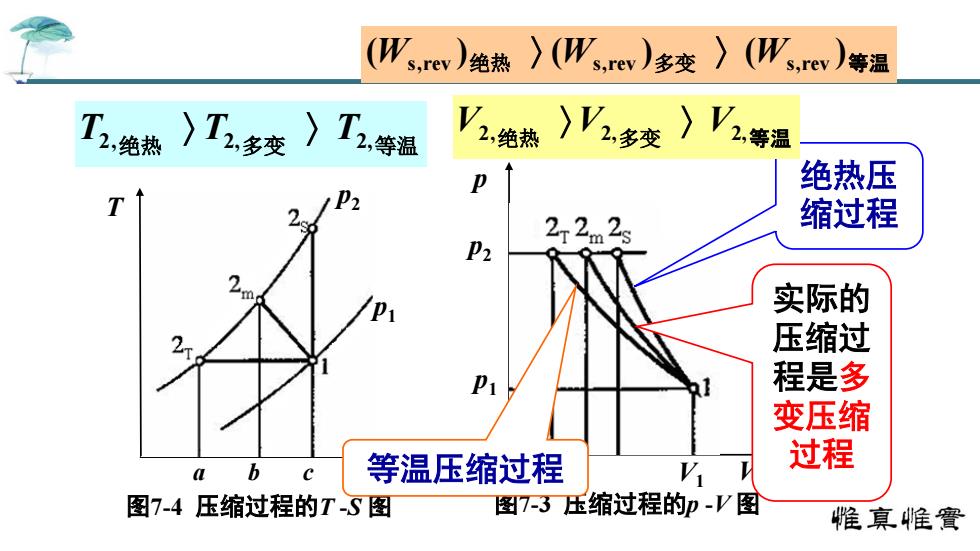
(W,rev)绝热)(W,rev)多变〉(W,rev等温 T2,给热)T多变)T2,等温 绝热压 2 缩过程 P2 么m 2 实际的 压缩过 程是多 变压缩 等温压缩过程 过程 b V 图7-4压缩过程的T-心图 图3压缩过程的p-V图 惟真帷實
T 图7-4 压缩过程的T -S 图 S p1 p2 a b c p 图7-3 压缩过程的p -V 图 V p1 p2 V1 实际的 压缩过 程是多 变压缩 等温压缩过程 过程 绝热压 缩过程 2,绝热 2,多变 2,等温 T 〉 T 〉 T (Ws,rev )绝热 〉 (Ws,rev )多变 〉 (Ws,rev )等温 2,绝热 2,多变 2,等温 V 〉V 〉 V

=O时,p=常数,等压过程; ◆ 等温过程方程式 1时,pV=常数,等温过程; PV=P,V2=pV k时,pVk=常数,等熵(绝热) 过程; ◆绝热过程方程式 m→士oo时,V=常数,等容过程。 P Vk=PV=PVk ◆实际(多变)过程方程 k为绝热指数 piVim=paVam=pym 1<m<k m为多变过程指数 惟真帷實
等温过程方程式 绝热过程方程式 实际(多变)过程方程 p1 V1 = p2 V2 = pV k k k p1 V1 = p2 V2 = pV m m m p1 V1 = p2 V2 = pV 1< < m k m=0时,p =常数,等压过程; m=1时,pV =常数,等温过程; m= k时,pV k =常数,等熵(绝热) 过程; m→±∞时,V =常数,等容过程。 k为绝热指数 m为多变过程指数

若为可逆过程,按照“得功为正(或耗功为负)”的规 定,其轴功: (W)nvdp (7-1) 惟真帷竇
若为可逆过程,按照“得功为正(或耗功为负)”的规 定,其轴功: (7-1) ∫ = 2 1 ( s,rev ) d p p W n V p

◆理想气体等温、多变及绝热压缩过程的方程式代入式 (7-1)积分得理论功耗的计算式。(单级压缩过程) w)$强=RT,In2=p,血马 (7-2a) (7-3a) w.n-tr (7-4a) 惟真帷竇
理想气体等温、多变及绝热压缩过程的方程式代入式 (7-1)积分得理论功耗的计算式。(单级压缩过程) 1 2 1 1 1 2 s,rev 1 ( ) ln ln p p p V p p W 等温 = RT = − − = − 1 1 ( ) 1 1 2 s,rev 1 k k p p RT k k W 绝热 − − = − 1 1 ( ) 1 1 2 s,rev 1 m m p p RT m m W 多变 (7-2a) (7-3a) (7-4a)

◆理想气体等温、多变及绝热压缩过程的理论功耗的计 算式。(单级压缩过程) Wlsa=xa台-AKn分 P 后jgw 7 k 、m- (W)多变= 惟真帷竇
理想气体等温、多变及绝热压缩过程的理论功耗的计 算式。(单级压缩过程) 1 2 1 1 1 2 s,rev 1 ( ) ln ln p p p V p p W 等温 = nRT = − − = − 1 1 ( ) 1 1 2 s,rev 1 k k p p nRT k k W 绝热 − − = − − = − − 1 1 1 1 ( ) 1 1 2 1 1 1 1 2 s,rev 1 m m m m p p p V m m p p nRT m m W 多变 − − = − 1 1 1 1 2 1 1 k k p p p V k k

压缩过程:状态1→状态2 ◆对pVT关系 p:低→高;:大→小:T:低→高 ◆状态能量:低→高 ◆三种压缩过程耗功量W、,rev 绝热>多变>等温 对真实气体,其耗功的计算公式又将如何? 惟真帷竇
对pVT关系 p:低→高;V:大→小:T:低→高 状态能量:低→高 三种压缩过程耗功量Ws,rev 绝热>多变>等温 压缩过程:状态1→状态2 对真实气体,其耗功的计算公式又将如何?