E(F)dr dF (山 dt 在某一时间t时,f(t)和F()之间的关系为: F0=f( f(t)= dF(t) di
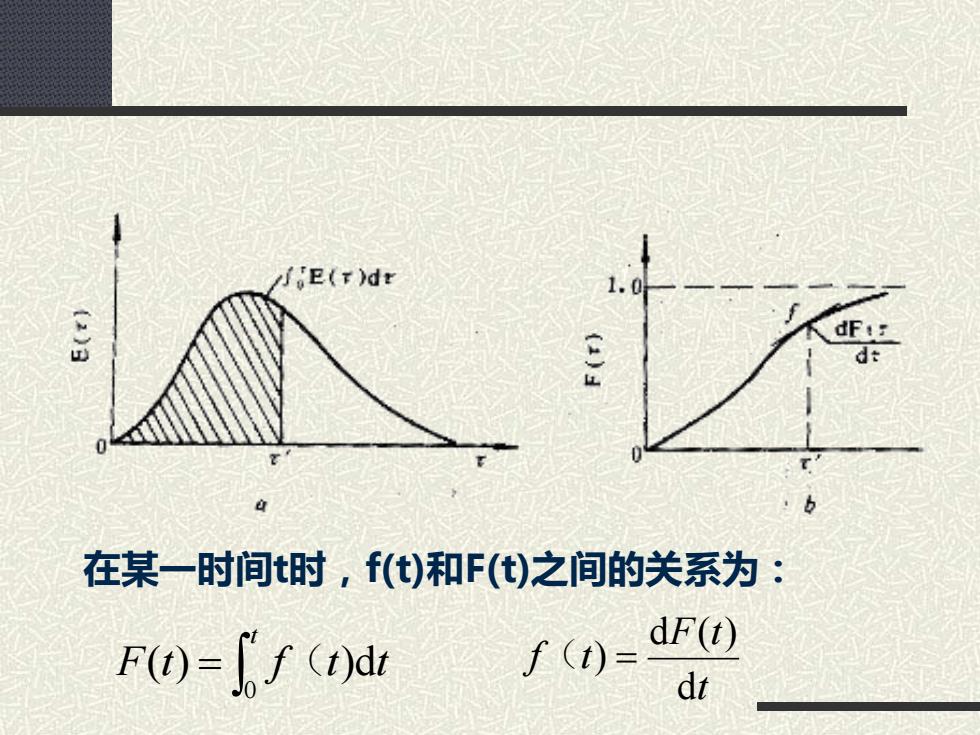
在某一时间t时,f(t)和F(t)之间的关系为: = t F t f t t 0 ( ) ( )d t F t f t d d ( ) ( ) =

6.2.2停留时间分布的实验测定 应答技术 示踪剂:光学的、电学的、化学的、放射性的 (1)尽可能与主流体物理性质一致 (2)易于检测,浓度很低时也能检测。 (3)不发生相转移或被吸附 (4)易于转变为电信号或光信号以便于采集数据 测定常用方法 脉冲法 阶跃法 周期输入法
6.2.2停留时间分布的实验测定 应答技术 示踪剂:光学的、电学的、化学的、放射性的 (1)尽可能与主流体物理性质一致 (2)易于检测,浓度很低时也能检测。 (3)不发生相转移或被吸附 (4)易于转变为电信号或光信号以便于采集数据 测定常用方法: 脉冲法 阶跃法 周期输入法
1.阶跃法 Co C() C() C() =0 0 t t 输入曲线 Co=C(oo) 响应曲线
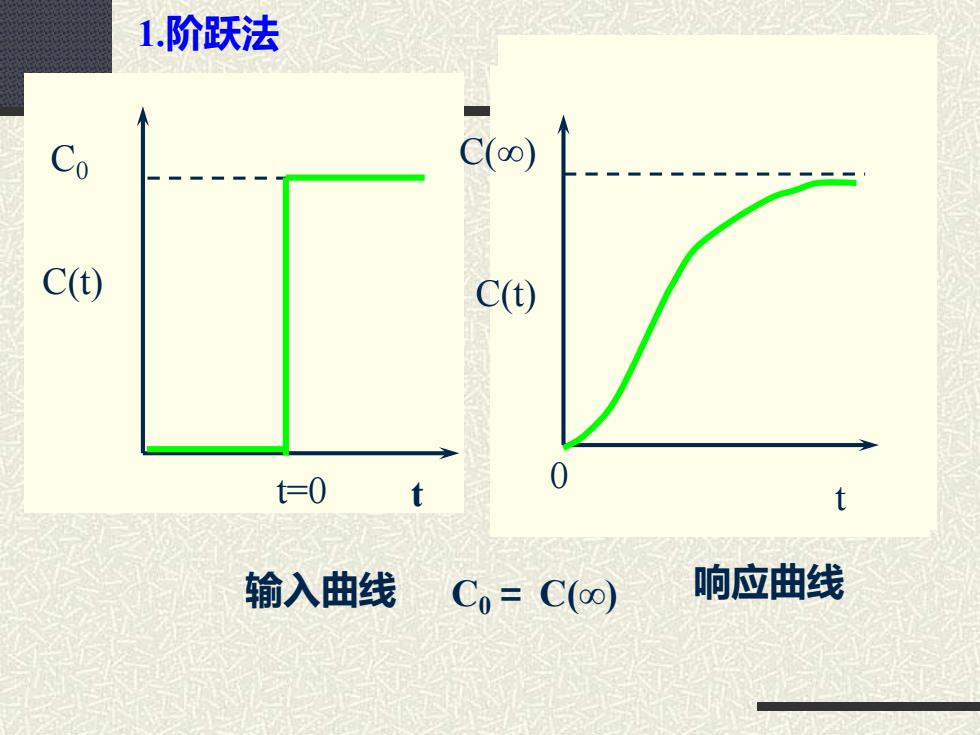
c(∞) c(t) t 0 输入曲线 响应曲线 C(∞) C(t) t 0 1.阶跃法 C0= C(∞) C0 C(t) t=0 t

1.阶跃法 ■L 由图可知,在仁0时,C=0;t↑,C一· Co; 时间为时,出口物料中示踪剂浓度为C),物料流量 为V,所以示踪剂流出量为VC(),又因为在时间为t 时流出的示踪剂,也就是反应器中停留时间小于的 示踪剂,按定义,物料中停留时间小于的粒子所占 的分率为F),因此,当示踪剂入口流量为VC时, 出▣流量VC,F),所以有: VCF(t)=VC(t) ∴.F(t)=C(t)/Co 因此,用此法可直接方便地测定实际反应器的留时间 分布函数
1.阶跃法 ◼ 由图可知,在t=0时,C=0;t , C C0 ; ◼ 时间为t时,出口物料中示踪剂浓度为C(t),物料流量 为V,所以示踪剂流出量为V C(t),又因为在时间为t 时流出的示踪剂,也就是反应器中停留时间小于t的 示踪剂,按定义,物料中停留时间小于t的粒子所占 的分率为F(t),因此,当示踪剂入口流量为VC0时, 出口流量VC0 F(t),所以有: ◼ 因此,用此法可直接方便地测定实际反应器的留时间 分布函数。 0 0 ( ) ( )/ ( ) ( ) F t C t C VC F t VC t = =
2.脉冲法 Co C() C() 0 0 t 输入曲线 响应曲线
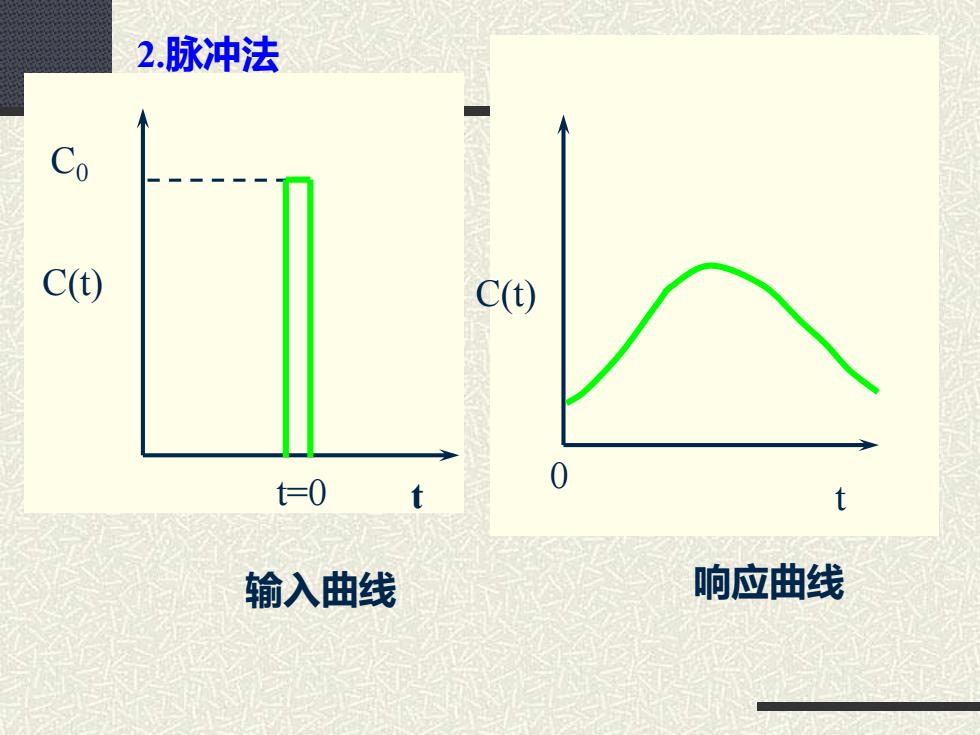
c(∞) c(t) t 0 C0 C(t) t=0 t 输入曲线 响应曲线 C(t) t 0 2.脉冲法

2.脉冲法 由于M=VCot,C,及t难以准确测量,故示踪剂的 总量可用出口所有物料的加和表示: M-[vC(o=vC(o C() [c(oar 因此,利用脉冲法可以很方便的测出停留时间分布密 度
2.脉冲法 由于M=VC0 Δt0, C0 及Δt0难以准确测量,故示踪剂的 总量可用出口所有物料的加和表示: 因此,利用脉冲法可以很方便的测出停留时间分布密 度。 C t t C t C t M V f t M VC t t V C t t ( )d ( ) ( ) ( ) ( )d ( )d 0 0 0 = = = =

3.脉冲法和阶跃法的比较 脉冲法 阶跃法 示踪剂 在原有的流股中加入 将原有流股换成流量与 注入方 示踪剂,不改变原流 其相同的示踪剂流股 法 股流量 dF(t) dc(t) f 可直接测得 f()= dt Codt F F()=[c(= [C(ndr Cox 可直接测得
3.脉冲法和阶跃法的比较 脉冲法 阶跃法 示踪剂 注入方 法 在原有的流股中加入 示踪剂,不改变原流 股流量 将原有流股换成流量与 其相同的示踪剂流股 f(t) 可直接测得 F(t) 可直接测得 C t dt C t dt F t C t dt t t = = 0 0 0 ( ) ( ) ( ) ( ) C t C t t F t f t d d ( ) d d ( ) ) 0 ( = =

6.2.3停留时间分布的数字特征 1数学期望:所有质点停留时间的“加权平均值” is ro)dh [f(dr dde-fdF f(t)dt=dF(t) F():所有停留时间为0一的质点所占的分率 F(t+d):所有停留时间为0一t+dt的质点所占的分率 dF(t)=F(t+dt)-F(t) dF():所有停留时间为t一+dt的质点所占的分率
6.2.3停留时间分布的数字特征 1.数学期望:所有质点停留时间的“加权平均值” f(t)dt=dF(t) F(t):所有停留时间为0—t的质点所占的分率 F(t+dt):所有停留时间为0—t+dt的质点所占的分率 dF(t)= F(t+dt)- F(t) dF(t):所有停留时间为t—t+dt的质点所占的分率 = = = = = 1 0 0 0 0 0 ( ) ( ) ( ) ( ) ( ) dt tdF t dt dF t t f t dt t f t dt t f t dt t t m

6.2.3停留时间分布的数字特征 2.方差:各个物料质点停留时间与平均停时间t差 的平方的加权平均值。 o-oa-I0-if0hrua-i [f(dr 方差是停留时间分布离散程度的量度 方差越小,越接近平推流 对平推流,各物料质点的停留时问相等,故t= 方差为零
2.方差:各个物料质点停留时间t与平均停时间 差 的平方的加权平均值。 方差是停留时间分布离散程度的量度 方差越小,越接近平推流 对平推流,各物料质点的停留时间相等,故 方差为零。 2 0 2 0 2 0 0 2 2 ( ) ( ) ( ) ( ) ( ) ( ) = − = − − = t t f t dt t f t dt t f t dt t t f t dt t t t = t 6.2.3停留时间分布的数字特征
6.2.4理想流型的停留时间分布 一、 平推流(PFR)F(t)=P{residence timetm f(t) 用数学上的6函数可表为: f(t)=8(t-t) tm
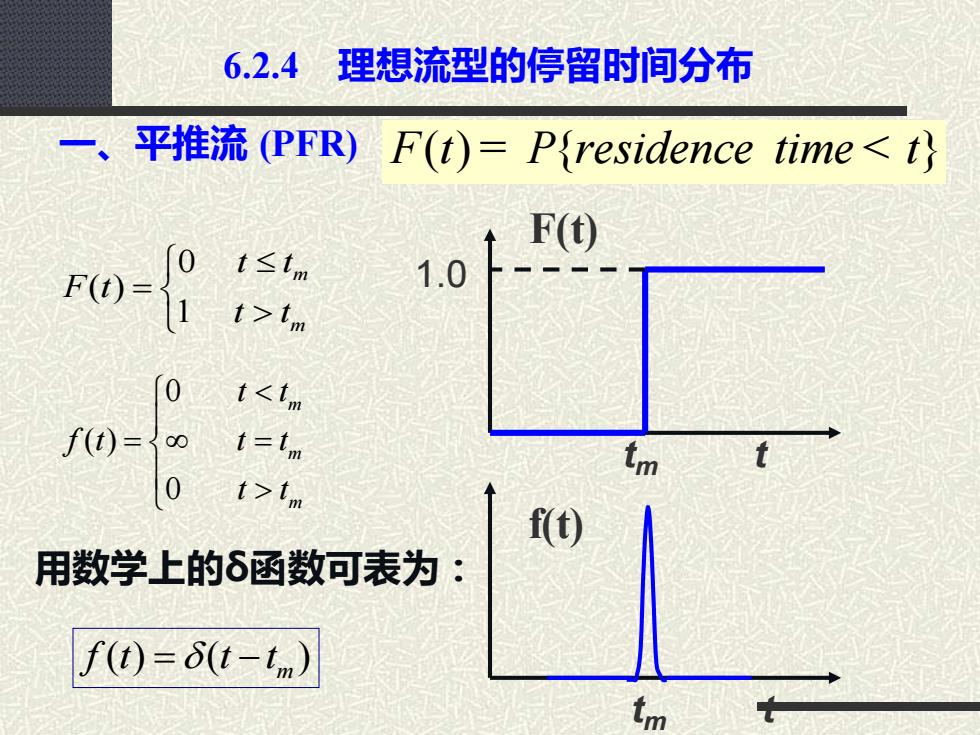
6.2.4 理想流型的停留时间分布 一、平推流 (PFR) F t P residence time t ( ) { } = < 0 ( ) 1 m m t t F t t t = tm t f(t) tm t F(t) 1.0 0 ( ) 0 m m m t t f t t t t t = = ( ) ( ) m f t t t = − 用数学上的δ函数可表为: