
第一章流体流动 1.0概述 1.1流体的物理性质 1.2流体静止的基本方程 1.3流体流动的基本方程 1.4流体流动现象 1.5流动阻力的计算 1.6管路计算 1.7流量测量
第一章 流体流动 1.0 概述 1.1 流体的物理性质 1.2 流体静止的基本方程 1.3 流体流动的基本方程 1.4 流体流动现象 1.5 流动阻力的计算 1.6 管路计算 1.7 流量测量

1.0概述 流体:具有流动性质的物体称为流体。包 括气体和液体。 流体的特性:流动性;无固定形状,随容 器的形状而变化;在外力作用下其内部发生相 对运动。 流体流动规律在化工生产中的应用: √解决流体的输送问题; √压力、流速、流量的测量; √为强化设备能力提供适宜的条件
1.0 概述 流体:具有流动性质的物体称为流体。包 括气体和液体。 流体的特性:流动性;无固定形状,随容 器的形状而变化;在外力作用下其内部发生相 对运动。 流体流动规律在化工生产中的应用: ✓解决流体的输送问题; ✓压力、流速、流量的测量; ✓为强化设备能力提供适宜的条件
1.1流体的物理性质 1.1.1连续介质的假定 1.1.1.1连续介质 Am/AV P(x,y. 质量△m 体积△V △V △V 将大量分子构成的集团称为质点,其大小与容器 或管路的尺寸相比微不足道。流体就是由无数个质点 所构成的,质点在流体内部一个紧挨一个,之间无间 隙,所以流体是连续的,叫连续介质
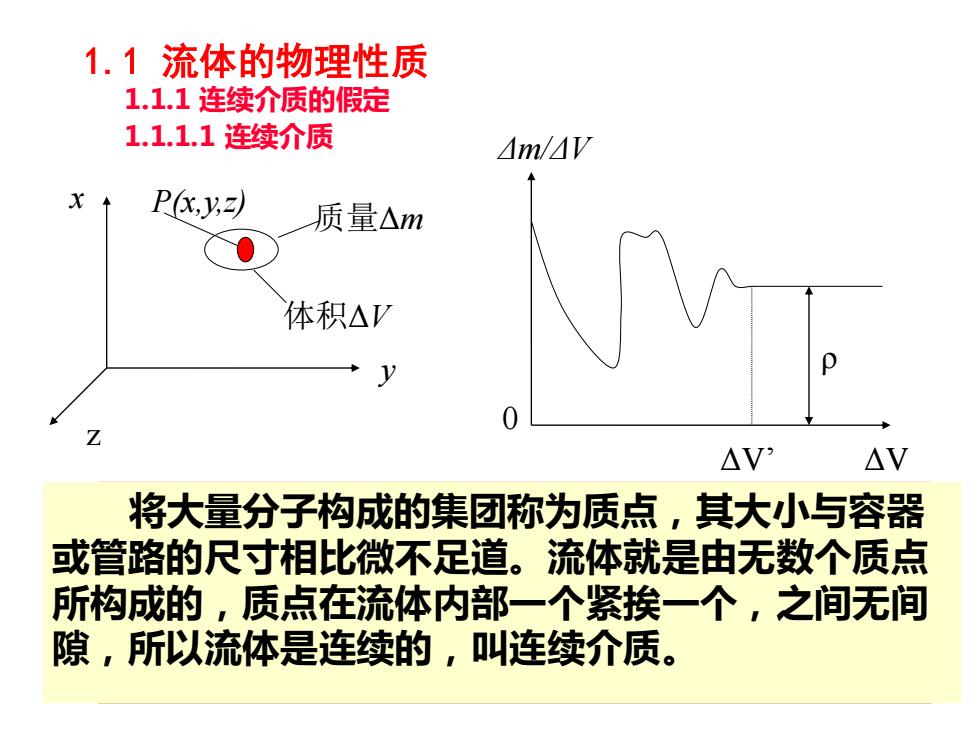
1.1 流体的物理性质 1.1.1 连续介质的假定 1.1.1.1 连续介质 P(x,y,z) 体积ΔV 质量Δm y x z Δm/ΔV ΔV 0 ΔV’ ρ 当包含点P(x,y,z)的微元体积ΔV< ΔV’时,随机进入和跃 出此体积的分子数不能时时平衡,即产生分子数的随机 波动,从而导致了ΔV内的流体的平均密度也随机波动, 此时流动表现出分子的个性。 ΔV≥ ΔV’时,平均密度逐 渐趋于一个确定的极限值,且不随微元体积的增大而改 变。 可见, ΔV’是一特征体积,它表示当几何尺寸很小但包含 足够多分子时的体积。其流体的宏观特性即为其中的分 子统计平均特性,此微元体积中的所有流体分子的集合 称为流体质点。 而流体就是由连续分布的流体质点所组成。 将大量分子构成的集团称为质点,其大小与容器 或管路的尺寸相比微不足道。流体就是由无数个质点 所构成的,质点在流体内部一个紧挨一个,之间无间 隙,所以流体是连续的,叫连续介质

1.1.1.2.流体的物理量 描述流体性质及其运动规律的物理量很多,如密 度、压力、组成、速度、温度等。据连续介质假定, 任何空间点上流体的物理量都是指位于该点上的流体 质点的物理量。如密度: Am △m p=lim → 4→A'V 4→0V 任意空间点上流体质点的物理量在任意时刻都有确定的数 值,即流体的物理量是空间位置和时间的函数,如: p=p(xy,ze);u=u(xyze);t=t(x,y,z e) 密度场 速度场 温度场
1.1.1.2.流体的物理量 任意空间点上流体质点的物理量在任意时刻都有确定的数 值,即流体的物理量是空间位置和时间的函数,如: ρ=ρ(x,y,z,θ); u=u(x,y,z,θ);t=t(x,y,z, θ) 密度场 速度场 温度场 V m lim V m lim V V' V' V → →0 = = 很小 描述流体性质及其运动规律的物理量很多,如密 度、压力、组成、速度、温度等。据连续介质假定, 任何空间点上流体的物理量都是指位于该点上的流体 质点的物理量。如密度:

1.1.2流体的密度 定义:单位体积流体所具有的质量称为密度,用p 表示,单位kg/m3。其表达式: V 密度为流体的物性参数,随温度、压力而变化。 1.1.2.1.纯液体的密度 液体的密度一般只随温度而变化,压力的影响可忽 略不计。纯液体的密度可从有关手册中查取
1.1.2 流体的密度 定义:单位体积流体所具有的质量称为密度,用ρ 表示,单位kg/m3 。其表达式: V m = 密度为流体的物性参数,随温度、压力而变化。 1.1.2.1. 液体的密度一般只随温度而变化,压力的影响可忽 略不计。纯液体的密度可从有关手册中查取

1.1.2.2.纯气体的密度 气体的密度与温度和压力有关。一般当压力不太高、温度 不太低的情况下,可按理想气体处理。这样,纯气体的密度计 算公式为: 1.根据查得状态计算 PVP'V.p2 p 上标“”表查的状态 T T 无上标表操作状态 PT 即:p=p' DIT 2.根据标准状态计算 PoVo T To 下标“0”表标准状态 M PTo 无下标表操作状态 即:p= 22.4PT
1.1.2.2.纯气体的密度 气体的密度与温度和压力有关。一般当压力不太高、温度 不太低的情况下,可按理想气体处理。这样,纯气体的密度计 算公式为: 1.根据查得状态计算 P' T PT' ' T' P' T p T' P'V' T PV ' m m = = = 即: 2.根据标准状态计算 PT PT . M T PV T p T PV T PV m 0 0 0 0 0 0 0 0 22 4 = = = 即: 上标“′”表查的状态 无上标表操作状态 下标“0”表标准状态 无下标表操作状态

3.根据操作状态计算 PV=nRT pm=m RT PM 即:p= RT 1.1.2.3液体混合物的平均密度 对理想溶液,各组分混合前后体积不变,则1kg混合液体的 体积等于各组分单独存在时的体积之和。即混合液体的密度Pm 可按下式计算: 1/pm=Σa/p 式中:a~组分在混合物中的质量分率; P-组分单独存在时密度,kg/m3
3.根据操作状态计算 RT PM RT M m m PV nRT P = = = 即: 1.1.2.3 液体混合物的平均密度 对理想溶液,各组分混合前后体积不变,则1kg混合液体的 体积等于各组分单独存在时的体积之和。即混合液体的密度ρm 1/ρm=Σai/ρi 式中:ai-组分i在混合物中的质量分率; ρi-组分i单独存在时密度,kg/m3

1.1.2.4气体混合物的平均密度 1.对理想气体,各组分混合前后质量不变 则1混合液体的质量等于各组分单独存在时 的质量之和。即混合气体的密度印m可按下式计 算: Pm=ΣyPi 式中:-组分在混合物中的体积分率(摩尔 分率); p-组分单独存在时密度,kg/m3
1.1.2.4 气体混合物的平均密度 1.对理想气体,各组分混合前后质量不变, 则1m3混合液体的质量等于各组分单独存在时 的质量之和。即混合气体的密度ρm可按下式计 ρm=Σyiρi 式中:yi-组分i在混合物中的体积分率(摩尔 分率); ρi-组分i单独存在时密度,kg/m3

2.仿照纯气体密度的计算: 0= Mn PTo 22.4T 式中:Mm-混合物平均分子量,kg/kmol。 Mm=∑My M-组分i的分子量,kg/kmol; -组分的摩尔分率。 3.仿照纯气体密度的计算: PMm Pm= RT
3.仿照纯气体密度的计算: 2.仿照纯气体密度的计算: PT PT . Mm 0 0 22 4 = 式中:Mm-混合物平均分子量,kg/kmol。 Mm=∑Miyi Mi-组分i的分子量,kg/kmol; yi-组分i的摩尔分率。 RT PMm m =

1.1.3流体的可压缩性、可压缩流体、不可压缩流体 1.1.3.1流体的可压缩性 定义:当作用于流体上的外力发生变化时,流体 的体积随之变化的特性。用压缩系数β表示: 1 du B=- v dp 式中:U-流体的比容,m3/kg B→流体愈容易被压缩
1.1.3 流体的可压缩性、可压缩流体、不可压缩流体 1.1.3.1 流体的可压缩性 定义:当作用于流体上的外力发生变化时,流体 的体积随之变化的特性。用压缩系数β表示: 式中:υ-流体的比容,m3/kg β↑→流体愈容易被压缩 dp d 1 = −