
第一章离散时间信号与系统
第一章 离散时间信号与系统

内容概要 1.1离散时间信号 1.2离散时间信号的傅里叶变换与z变换 1.3离散时间系统 1.4系统的频率响应及其系统函数 2
2 内容概要 1.4系统的频率响应及其系统函数 1.3离散时间系统 1.2离散时间信号的傅里叶变换与z变换 1.1离散时间信号

理解和熟悉离散时间信号的表示 和运算,离散系统的分类与判断 掌握离散时间信号各域的变换方 法,离散系统频率响应的求解和 第1章 系统函数分析法 营装 要求能根据序列函数画图;将信 3 号在各域之间转换;能根据判断 系统类型;能根据系统函数分析 系统性能
3 教学 目标 第1章 理解和熟悉离散时间信号的表示 1 和运算,离散系统的分类与判断 掌握离散时间信号各域的变换方 法,离散系统频率响应的求解和 系统函数分析法 2 要求能根据序列函数画图;将信 号在各域之间转换;能根据判断 系统类型;能根据系统函数分析 系统性能 3
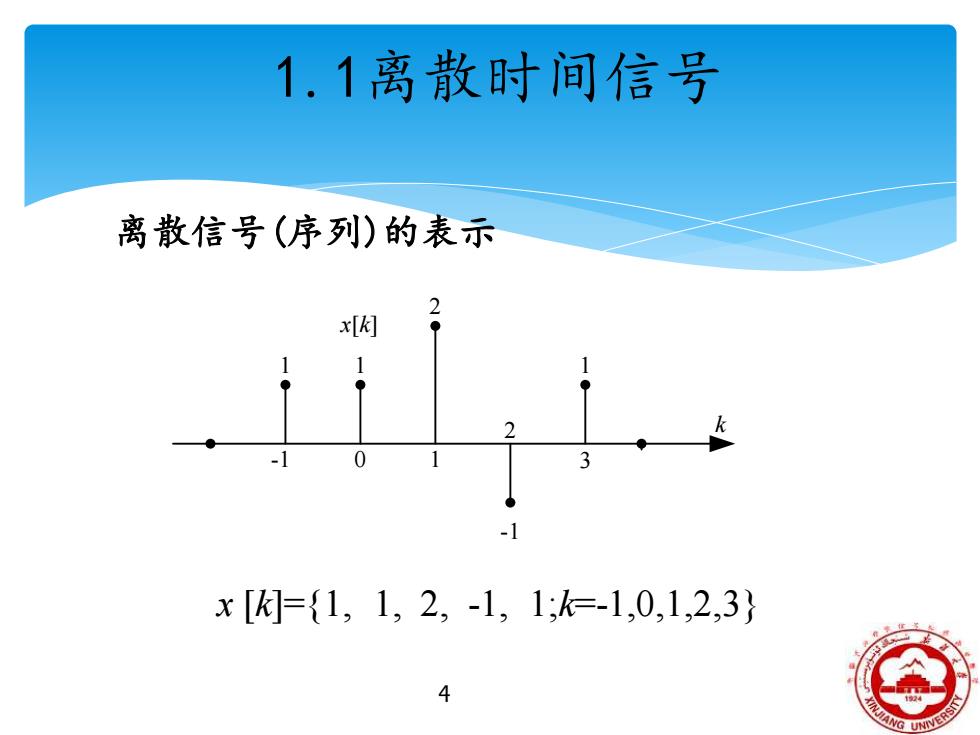
1.1离散时间信号 离散信号(序列)的表示 x[k] -1 x[={1,12,-1,1;k=-1,0,1,2,3} 4
4 1.1离散时间信号 x [k]={1, 1, 2, -1, 1;k=-1,0,1,2,3} k 1 2 1 -1 -1 0 1 2 3 x[k] 1 离散信号(序列)的表示

离散序列的产生 *对连续信号抽样x[n]=x(n) *信号本身是离散的 *计算机产生 注意: *离散信号: 时间上量化的信号 *数字信号:时间和幅度上都量化的信号 *注意:在通信原理中,不区分离散信号和数字信 号,二者都表示代表消息的参量取值是有限个离 散值,而不是用时间区分
对连续信号抽样 x[n]=x(nT) 信号本身是离散的 计算机产生 注意: 离散信号: 时间上量化的信号 数字信号: 时间和幅度上都量化的信号 注意:在通信原理中,不区分离散信号和数字信 号,二者都表示代表消息的参量取值是有限个离 散值,而不是用时间区分 5 离散序列的产生

常用序列 1.单位脉冲序列 8(n) on] 10 =0 n n≠0 2.单位阶跃序列 10 n≥0 n≤0 RN(n) 3.矩形序列 0≤n≤W-1 N- otherwise
常用序列 1.单位脉冲序列 = = 0 0 1 0 [ ] n n n 2.单位阶跃序列 = 0 0 1 0 [ ] n n u n 3.矩形序列 − = 0 otherwise 1 0 1 [ ] n N R N n
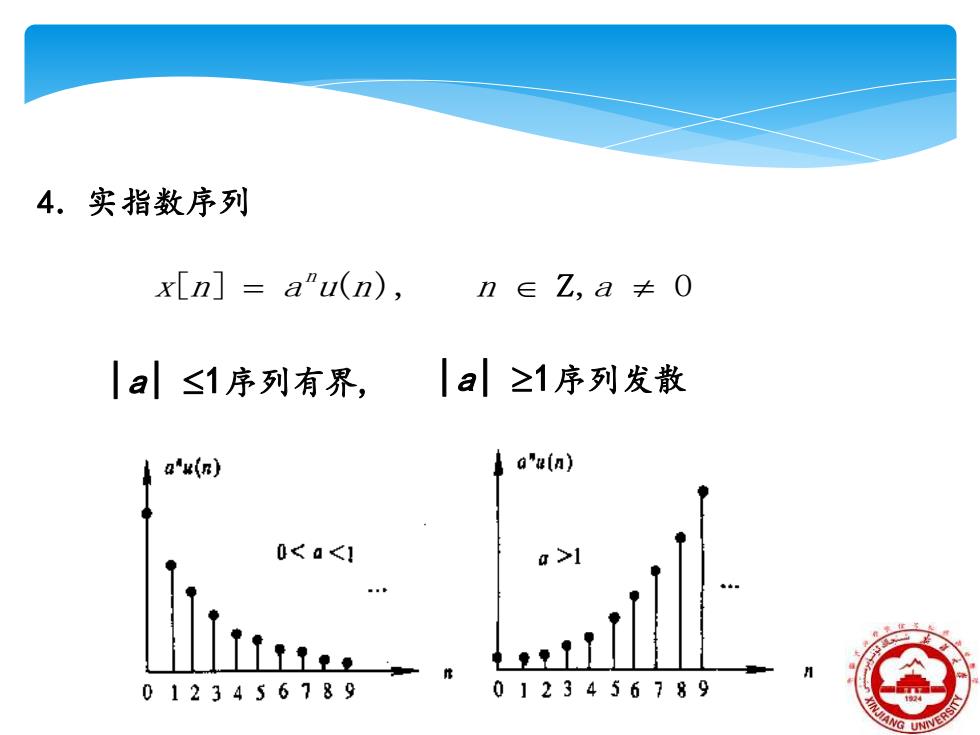
4.实指数序列 x[n]a"u(n), n∈Z,a≠0 |a≤1序列有界, |a≥1序列发散 a"u(n) a"u(n) 0 0123456789 0】23456789
4.实指数序列 x[n] = a u(n), n ,a 0 n Z |a| 1序列有界, |a| 1序列发散

5.正弦型序列 x(n)=Asin(on) (1) 式中,A为幅度,ω为数字角频率,单位为孤度。 考虑数字正弦是由模拟信号x(t)=Asin2t 采样得到.即 x(n)=xa(t)n=Asin(SnT) (2) 数字域频率和模拟信号角频率的对应关系 比较(1)、(2)两式得 0=2T= 2 f 「Ω单位:弧度/秒连续 连续域的角频率 o单位:弧度 连续 离散域的角频率
式中,A为幅度,ω为数字角频率,单位为弧度。 考虑数字正弦是由模拟信号 采样得到,即 ( ) ( ) sin( ) (2) a t nT x n x t A nT = = = x n A n ( ) sin( ) (1) = ( ) sin a x t A t = 数字域频率和模拟信号角频率的对应关系 s T f 比较(1)、(2)两式得 = = 5.正弦型序列 单位 : 弧度 连续 离散域的角频率 单位 : 弧度/秒 连续 连续域的角频率 (− , )
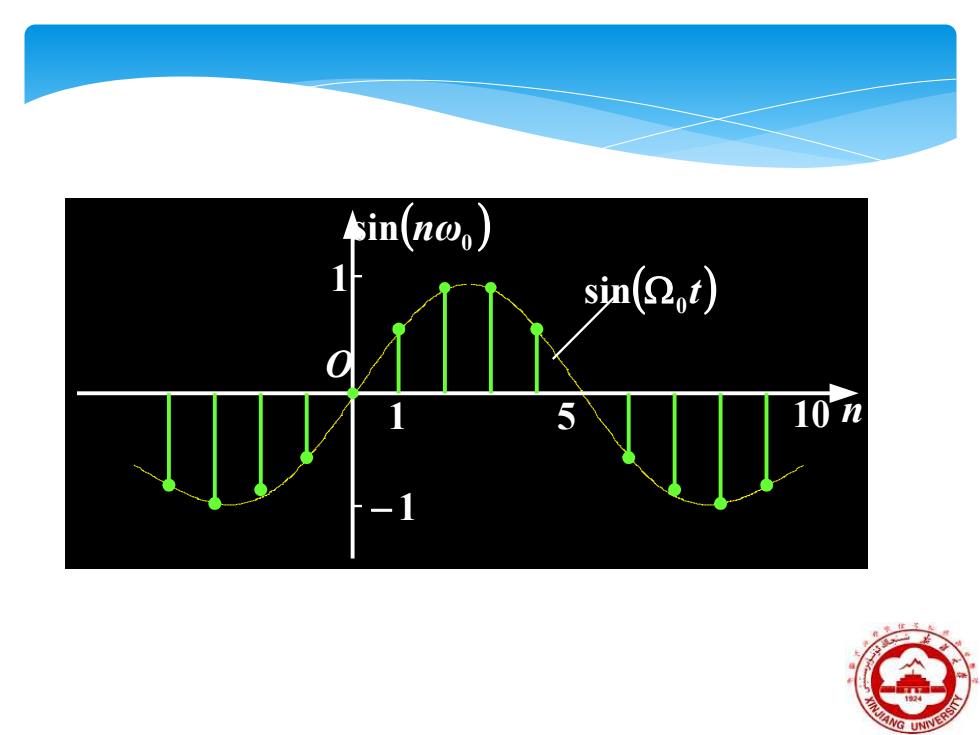
sin n@o) sin(2t)
1 5 O n − 1 10 ( ) 0 sin nω ( t) 0 1 sin

6.复指数序列(Complex exponential sequence) x(n)=e(a+jo)n 还可写成 x(n)=e"[cos(on)+jsin(on)] 这里ω为数字域频率,单位为孤度。当0=0时,上式可 表示成虚指数序列 x(n)=eio"cos(@n)+jsin(@n)
6.复指数序列(Complex exponential sequence) ( ) ( ) j n x n e + = 这里ω为数字域频率,单位为弧度。当σ=0时,上式可 表示成虚指数序列 ( ) [cos( ) sin( )] n x n e n j n = + ( ) cos( ) sin( ) j n x n e n j n = = + 还可写成