
192 AINJIANG UNIVERSIT 第6章 数字信号处理系统的实现
第 6 章 数字信号处理系统的实现

本章主要内容 *|IR滤波器结构 *FIR滤波器结构 *有限字长效应
IIR滤波器结构 FIR滤波器结构 有限字长效应 本章主要内容

引言 数字滤波器的实现方法: a.利用专用计算机: b.直接利用计算机和通用软件编程实现。 一个数字滤波器的系统函数一般可表示为有理函数形式: a,z H(z)=-i=0 1-∑b,z 为IIR滤波器形式,{b,}都为O时就是一个FIR滤波器。 对于这样一个系统,也可用差分方程来表示: y(m)=∑axn-0+∑b,yn-) i-
引言 数字滤波器的实现方法: a. 利用专用计算机; b.直接利用计算机和通用软件编程实现。 一个数字滤波器的系统函数一般可表示为有理函数形式: 为I I R滤波器形式,{ }都为0时就是一个FIR滤波器。 对于这样一个系统,也可用差分方程来表示:

即一个输出序列是其过去点的线性组合加上当前输入 序列与过去N点输入序列的线性组合。y()除了与当前的输 入x()有关,同时还与过去的输入和过去的输出有关,系统 是带有记忆的。 对于上面的算式,可以化成不同的计算形式,如直接计 算、分解为多个有理函数相加、分解为多个有理函数相乘等 等,不同的计算形式也就表现出不同的计算结构,而不同的 计算结构可能会带来不同的效果,或者是实现简单,编程方 便,或者是计算精度较高等等。 另外,数字信号是通过采样和转换得到的,而转换的位 数是有限的(一般6、8、10、12、16位),所以存在量化误 差,另外,计算机中的数的表示也总是有限的,经此表示的 滤波器的系数同样存在量化误差,在计算过程中因有限字长 也会造成误差
即一个输出序列是其过去 点的线性组合加上当前输入 序列与过去 点输入序列的线性组合。 除了与当前的输 入 有关,同时还与过去的输入和过去的输出有关,系统 是带有记忆的。 对于上面的算式,可以化成不同的计算形式,如直接计 算、分解为多个有理函数相加、分解为多个有理函数相乘等 等,不同的计算形式也就表现出不同的计算结构,而不同的 计算结构可能会带来不同的效果,或者是实现简单,编程方 便,或者是计算精度较高等等。 另外,数字信号是通过采样和转换得到的,而转换的位 数是有限的(一般6、8、10、12、16位),所以存在量化误 差,另外,计算机中的数的表示也总是有限的,经此表示的 滤波器的系数同样存在量化误差,在计算过程中因有限字长 也会造成误差。N N y(n) x(n)
x(n)→ DF☐y(n IIR、FIR的系统函数 网络结构形式 软、硬件实现
IIR、FIR的系统函数 网络结构形式 软、硬件实现 DF

量化误差主要有三种误差: ①A/D变换量化效应; ②系数的量化效应; ③数字运算的有限字长效应
量化误差主要有三种误差: ①A/D变换量化效应; ②系数的量化效应; ③数字运算的有限字长效应

1924 6.1数字滤波器的结构
6.1 数字滤波器的结构
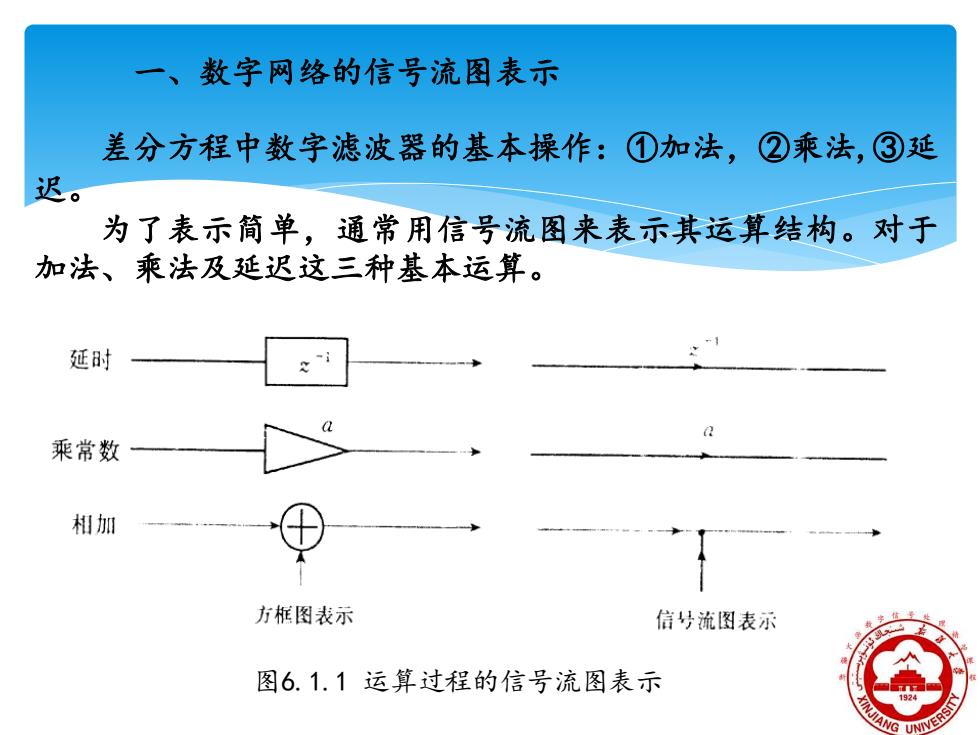
一、数字网终的信号流图表示 差分方程中数字滤波器的基本操作:①加法,②乘法,③延 迟。 为了表示简单,通常用信号流图来表示其运算结构。对于 加法、乘法及延迟这三种基本运算。 延时 乘常数 相加 方框图表示 信号流图表示 图6.1.1运算过程的信号流图表示
一 、数字网络的信号流图表示 差分方程中数字滤波器的基本操作:①加法,②乘法,③延 迟。 为了表示简单,通常用信号流图来表示其运算结构。对于 加法、乘法及延迟这三种基本运算。 图6.1.1 运算过程的信号流图表示
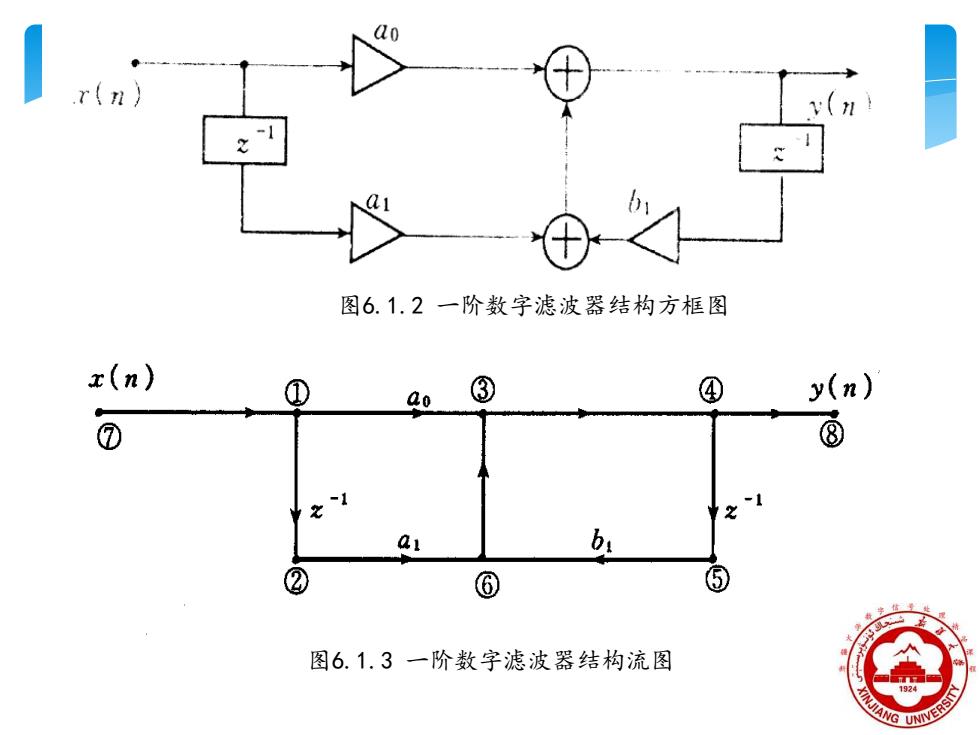
20 图6.1.2一阶数字滤波器结构方框图 x(n) ③ ④ y(n) ⑦ ⑧ ② ⑥ 图6.1.3一阶数字滤波器结构流图
图6.1.3 一阶数字滤波器结构流图 图6.1.2 一阶数字滤波器结构方框图

y(n)=aox(n)+ax(n-1)+by(n-1) 只有输出支路的节,点称为输入节点或源,点; 只有输入支路的节点称为输出节,点或阱点, 既有输入支路又有输出支路的节点叫做混合节点。 通路是指从源点到阱点之间沿着箭头方向的连续的一串 支路,通路的增益是该通路上各支路增益的乘积。 回路是指从一个节点出发沿着支路箭头方向到达同一个 节点的闭合通路,它象征着系统中的反馈回路。组成回 路的所有支路增益的乘积通常叫做回路增益
只有输出支路的节点称为输入节点或源点; 只有输入支路的节点称为输出节点或阱点; 既有输入支路又有输出支路的节点叫做混合节点。 通路是指从源点到阱点之间沿着箭头方向的连续的一串 支路,通路的增益是该通路上各支路增益的乘积。 回路是指从一个节点出发沿着支路箭头方向到达同一个 节点的闭合通路,它象征着系统中的反馈回路。组成回 路的所有支路增益的乘积通常叫做回路增益