
理 学 个 NJIANG NIVERST 1924 4.4 从模拟滤波器低通原型到各种数字滤 波器的频率变换(原型变换)
4.4 从模拟滤波器低通原型到各种数字滤 波器的频率变换(原型变换)
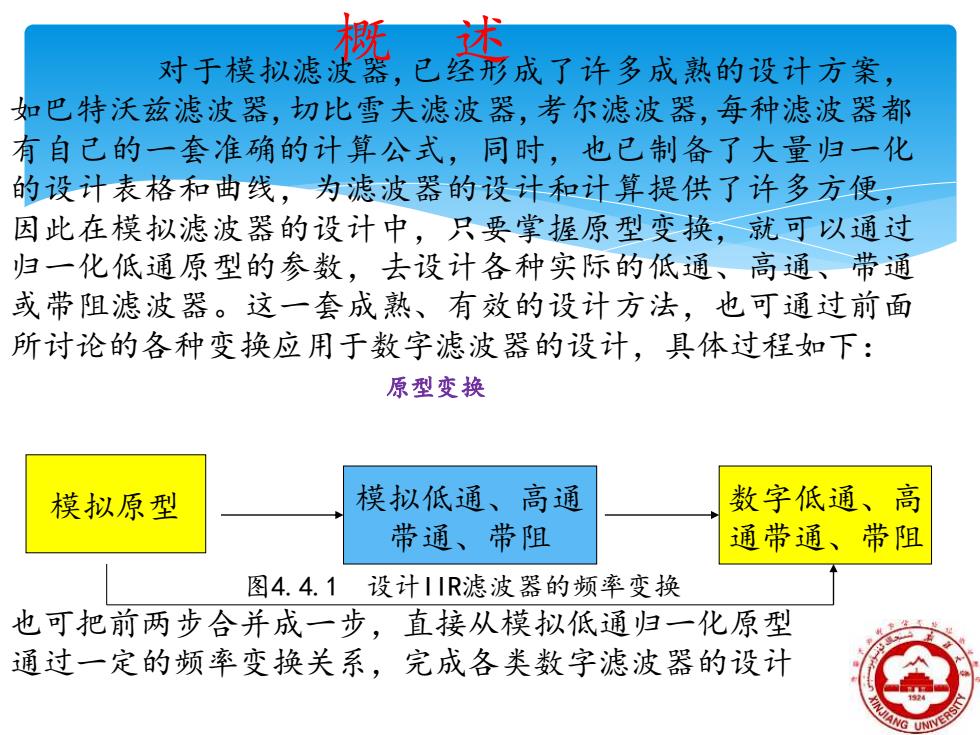
对于模拟滤波器,已经形成了许多成熟的设计方案, 如巴特沃滋滤波器,切比雪夫滤波器,考尔滤波器,每种滤波器都 有自己的一套准确的计算公式,同时,也已制备了大量归一化 的设计表格和曲线,为滤波器的设计和计算提供了许多方便, 因此在模拟滤波器的设计中,只要掌握原型变换,就可以通过 归一化低通原型的参数,去设计各种实际的低通、高通、带通 或带阻滤波器。这一套成熟、有效的设计方法,也可通过前面 所讨论的各种变换应用于数字滤波器的设计,具体过程如下: 原型变换 模拟原型 模拟低通、高通 数字低通、高 带通、带阻 通带通、带阻 图4.4.1设计IIR滤波器的频率变换 也可把前两步合并成一步,直接从模拟低通归一化原型 通过一定的频率变换关系,完成各类数字滤波器的设计
对于模拟滤波器,已经形成了许多成熟的设计方案, 如巴特沃兹滤波器,切比雪夫滤波器,考尔滤波器,每种滤波器都 有自己的一套准确的计算公式,同时,也已制备了大量归一化 的设计表格和曲线,为滤波器的设计和计算提供了许多方便, 因此在模拟滤波器的设计中,只要掌握原型变换,就可以通过 归一化低通原型的参数,去设计各种实际的低通、高通、带通 或带阻滤波器。这一套成熟、有效的设计方法,也可通过前面 所讨论的各种变换应用于数字滤波器的设计,具体过程如下: 原型变换 图4.4.1 设计IIR滤波器的频率变换 也可把前两步合并成一步,直接从模拟低通归一化原型 通过一定的频率变换关系,完成各类数字滤波器的设计 模拟原型 模拟低通、高通 带通、带阻 数字低通、高 通带通、带阻 概 述

给定数字滤波器的参数指标,通过模拟滤波器设计, 而后映射的方法设计数字滤波器H(z),设计步骤: 由数字滤波器参数指标来求解确定模拟滤波器参 数 设计模拟滤波器的低通原型(根据某些已知的 滤波器类型) -根据要求求解参数(阶数N,截止频率2。) 查表找出指定滤波器的的归一化系数得到Ha1(s) 转化为Ha(s)
给定数字滤波器的参数指标 , 通过模拟滤波器设计, 而后映射的方法设计数字滤波器 H(z),设计步骤: ➢ 由数字滤波器参数指标来求解确定模拟滤波器参 数 ➢ 设计模拟滤波器的低通原型(根据某些已知的 滤波器类型) -根据要求求解参数(阶数N,截止频率 ) -查表找出指定滤波器的的归一化系数得到Ha1(s) -转化为Ha(s) . C

少模拟数字频率变换-一 可选择不同的方法 A、脉冲响应不变法计算H(Z 1)、部分分式法分解Ha(s) Hs)=∑ S-Pk 2)、将模拟的极点{pk}转化为数字极点 [ekT},并得到数字滤波器 He)=1-e R me)m。分
= − = N k k k a s p R H s 1 ( ) ➢ 模拟数字频率变换-可选择不同的方法 A、脉冲响应不变法计算H(Z) 1)、部分分式法分解Ha(s) 2)、将模拟的极点 {pk} 转化为数字极点 {e pkT} ,并得到数字滤波器 = − − = N k p T k e z R H z 1 k 1 1 ( ) = = = T H e H j H j a T a j ( ) ( )

B、双线性变换法计算H(Z) 双线性变换比脉冲响应法的设计计算更直接和简单。 由于s与z之间的简单代数关系,所以从模拟传递函数 可直接通过代数置换得到数字滤波器的传递函数。 置换过程: 频响: Me==宁e2
B、双线性变换法计算H(Z) 双线性变换比脉冲响应法的设计计算更直接和简单。 由于s与z之间的简单代数关系,所以从模拟传递函数 可直接通过代数置换得到数字滤波器的传递函数。 置换过程: 频响: + − = = − − + − = − − 1 1 1 2 1 1 2 1 ( ) ( ) 1 1 z z T H z H s Ha z z T s a = = = 2 2 ( ) ( ) 2 2 t g T H e H j H j a t g T a j

举例讨论应用模拟滤波器低通原型,设计各种数字 滤波器的基本原理,着重讨论双线性变换法。 低通变换 通过模拟原型设计数字滤波器的四个步骤: 1)确定数字滤波器的性能要求,确定各临界频 率{ωk}。 2)由变换关系将{ω}映射到模拟域,得出模拟 滤波器的临界频率值{Ωk}。 3)根据{Ωk}设计模拟滤波器的H(s) 4)把H,(s)变换成H(z)(数字滤波器系统函数)
一 .低通变换 通过模拟原型设计数字滤波器的四个步骤: 1)确定数字滤波器的性能要求,确定各临界频 率{ωk}。 2)由变换关系将{ωk}映射到模拟域,得出模拟 滤波器的临界频率值{Ωk}。 3)根据{Ωk}设计模拟滤波器的Ha(s) 4) 把Ha(s)变换成H(z)(数字滤波器系统函数) 举例讨论应用模拟滤波器低通原型,设计各种数字 滤波器的基本原理,着重讨论双线性变换法

创4.41设采样周期T=250us(f三4khz 设计一个三阶巴特沃滋LP滤波器,其3dB截止频率fc=1khz。分 别用脉冲响应不变法和双线性变换法求解。 解:a.脉冲响应不变法 由于脉冲响不变法的频率关系是线性的,所以可直接 按Q。=2πf。设计Ha(s)。根据上节的讨论,以截止频率2。 归一化的三阶巴特沃兹滤波器的传递函数为: 1 Ha(s)= 1+2s+2s2+s 以5/2。代替其归一化频率,得: H,(s)=1+2s12,)+2s1Q2+(s1Q.J
例4.4.1 设采样周期 , 设计一个三阶巴特沃兹LP滤波器,其3dB截止频率fc=1khz。分 别用脉冲响应不变法和双线性变换法求解。 解:a. 脉冲响应不变法 由于脉冲响不变法的频率关系是线性的,所以可直接 按Ω c =2πfc设计Ha(s)。根据上节的讨论,以截止频率Ω c 归一化的三阶巴特沃兹 滤波器的传递函数为: 2 3 1 2 2 1 ( ) s s s Ha s + + + = 2 3 1 2( / ) 2( / ) ( / ) 1 ( ) c c c a s s s H s + + + = c s/ T 250 s( f 4khz) = s = 以 代替其归一化频率,得:

也可以查表得到。由手册中查出 巴特沃兹多项式的系数,之后以sQ 代替归一化频率,即得(s。 2。=2代入,就完 成了模拟滤波器的设计,但为简化运 算,减小误差积累,fc数值放到数字 滤波变换后代入
也可以查表得到。由手册中查出 巴特沃兹多项式的系数,之后以 代替归一化频率,即得 。 代入,就完 成了模拟滤波器的设计,但为简化运 算,减小误差积累,fc数值放到数字 滤波变换后代入。 Ha(s) c c = 2f c s/

为进行脉冲响应不变法变换,计算Ha(S)分母多项式的根, 将上式写成部分分式结构: a()= Dc -Sc/3ello -2c/3e-jnl6 s+2cs+2c(1-j√3)/28+2c1+jW3)/2 对照前面学过的脉冲响应不变法中的部分分式形式,有 A=2e,S1=-2e;A2=-2c/√5eπ/6 s2=-2.(1-j3)/2,4=-2c13r6,s=-2.1+jN3)12 将上式部分系数代入数字滤波器的传递函数: 极点S
为进行脉冲响应不变法变换,计算Ha(S)分母多项式的根, 将上式写成部分分式结构: (1 3)/ 2 / 3 (1 3)/ 2 / 3 ( ) / 6 / 6 s c j c e s c j c e s c c Ha s j j + + − + + − − + + = − /6 1 , 1 ; 2 / 3 j A = c s = −c A = −c e (1 3)/ 2; / 3 , 3 (1 3)/ 2 /6 2 3 s j A c e s j c j = −c − = − = − + − = − − = N i S T i e Z A H Z i 1 1 1 ( ) Si 对照前面学过的脉冲响应不变法中的部分分式形式 ,有 将上式部分系数代入数字滤波器的传递函数: 极点

并将2。=0。/T代入,得: @IT _+-(@.1V3)e6-(o.1V3Tem ④e。方 1-eo.1+/W/2Z 合并上式后两项,并将0。=2可T=0.5π 代入,计算得: =027 1.571 -1.571+0.5541Z 1-0.1905Z+0.2079Z-2
并将 代入,得: 合并上式后两项,并将 代入,计算得: (1 3)/ 2 1 / 6 (1 3)/ 2 1 / 6 1 1 ( / 3 ) 1 ( / 3 ) 1 / ( ) − + − − − − − − − − − + − − + − = e Z T e e Z T e e Z T H Z j j c j j C c c c c c = 2f c T = 0.5 − + − + + − = − − − − 1 2 1 1 1 0.1905 0.2079 1.571 0.5541 1 0.2079 1 1.571 ( ) Z Z Z T Z H Z c =c /T