
数字信号处理教案 (新疆大学信息学院数字信号处理课程组) 2014年9月
1 数 字 信 号 处 理 教 案 (新疆大学信息学院数字信号处理课程组) 2014 年 9 月
绪论第一节 绪论 一、从棋拟到数字 3、模拟信号是连续信号的特例。时间和幅度均连续。 4、离散信号:时间上不连续,幅度连续。 5、数字信号:幅度量化,时间和幅度均不连续 模拟信号 连续时间信号 数字信号 连续时间信号 模拟信号 采样 A/D 通用或专用 D/A 模拟低通 保持器 变换器 计算机 变换器 滤波器 数字信号处理系统 电 数字信号 采样保特信 ,D/A输出同号 0.750 量化电 极汉信 1000.0 00 11037 m10125 0000.000 0000.0 040600 15 02040600 12141 模拟信号的数字化 数字信号转化成模拟信号 D/A输出 棋拟滤波输出 05 1 1.5 50 150 200 150
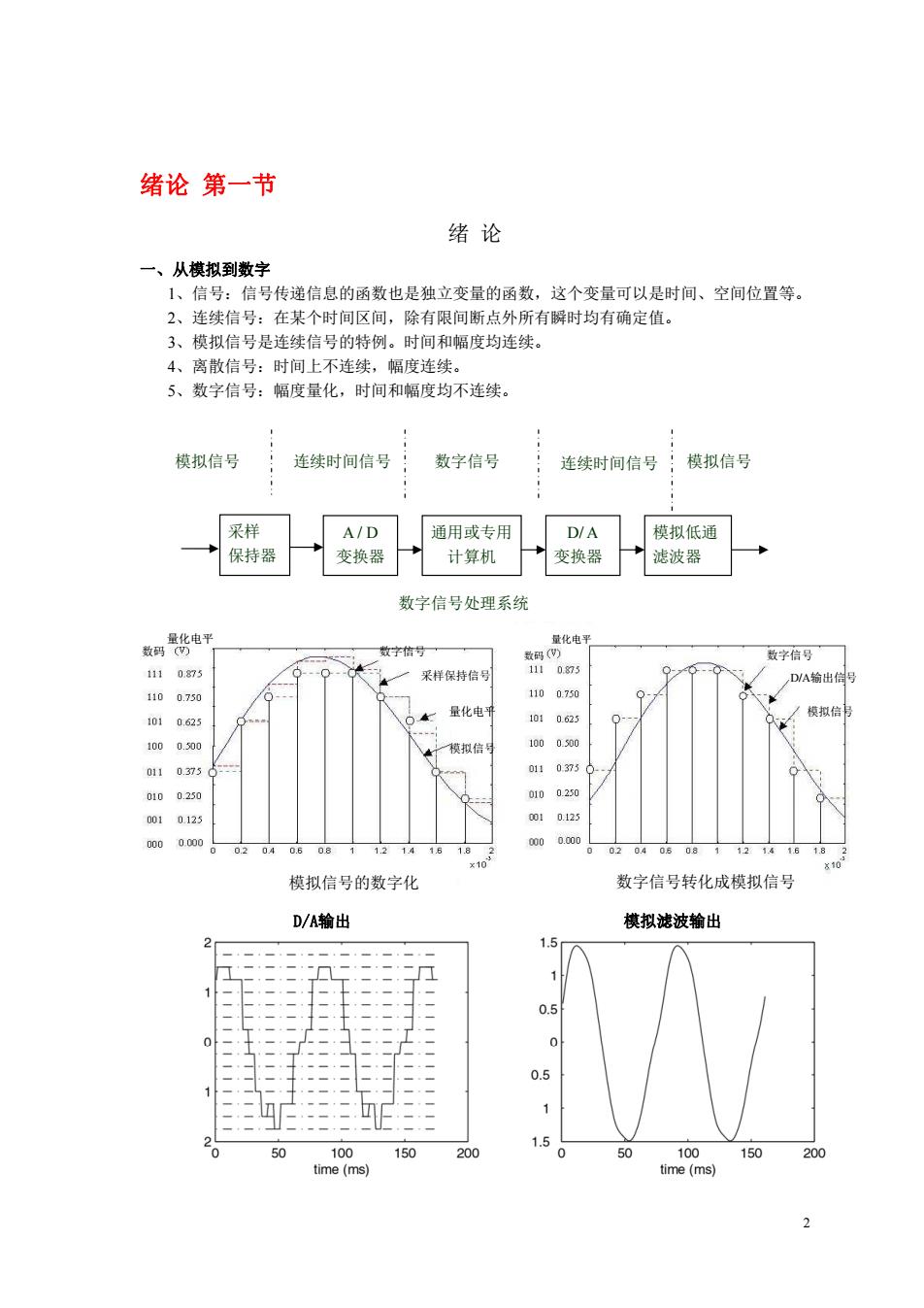
2 绪论 第一节 绪 论 一、从模拟到数字 1、信号:信号传递信息的函数也是独立变量的函数,这个变量可以是时间、空间位置等。 2、连续信号:在某个时间区间,除有限间断点外所有瞬时均有确定值。 3、模拟信号是连续信号的特例。时间和幅度均连续。 4、离散信号:时间上不连续,幅度连续。 5、数字信号:幅度量化,时间和幅度均不连续。 数码 量化电平 数字信号 D/A输出信号 模拟信号 数字信号转化成模拟信号 D/A输出 模拟滤波输出 模拟信号的数字化 数码 数字信号 量化电平 模拟信号 采样保持信号 量化电平 A / D 变换器 通用或专用 计算机 采样 保持器 D/ A 变换器 模拟低通 滤波器 模拟信号 数字信号 模拟信号 数字信号处理系统 连续时间信号 连续时间信号

二、数字信号处理的主要优点 数字信号处理采用数字系统完成信号处理的任务,它具有数字系统的一些共同优点,例如 抗干扰、可靠性强,便于大规模集成等。除此而外 与传统的模拟信号处理方法相比较,它还 些明显的优点 1、精度高 在模拟系统的电路中,元器件精度要达到10~以上已经不容易了,而数字系统17位字长可 以达到1Q~的精度,这是很平常的。例如,基于离散傅里叶变换的数字式频谱分析仪,其幅值 精度和频率分辨率均远远高于模拟频谱分析仪。 2、灵活性强 数字信号处理采用了专用或通用的数字系统,其性能取决于运算程序和乘法器的各系数, 这些均存储在数字系统中,只要改变运算程序或系数,即可改变系统的特性参数,比改变模拟 系续方便得多」 3、可以实现模拟系统很难达到的指标或特性 例如:有限长单位脉冲响应数字滤波器可以实现严格的线性相位 在数字信号处理中可以将信号存储起来,用延迟的方法实现非因果系统,从而提高了系统的性 能指标: 数据压缩方法可以大大地减少信息传输中的信道容量, 4、可以实现多维信号处理 利用庞大的存储单元 可以存储二维的图像信号或多维的阵列信号,实现二维或多维的滤 波及谱分析等。 5、缺点 (1)增加了系统的复杂性。他需要模拟接口以及比较复杂的数字系统 (2)应用的频率范围受到限制。主要是AD转换的采样频率的限制 (3)系统的功率消耗比较大。数字信号处理系 统中集成 了几十万甚至更多的晶体管,而模拟信 号处理系统中大量使用的是电阻、电容、电感等无源器件,随若系统的复杂性增加这一矛盾会 更加突出。 三、发展特点 (1)由简单的运算走向复杂的运算,目前几十位乘几十位的全并行乘法器可以在数个纳秒的时间 内完成一次浮点乘法运算,这无论在运算速度上和运算精度上均为复杂的数字信号处理算法提 供了先决条件 (2)由低频走向高频,模数转换器的采样频率已高达数百兆赫,可以将视频甚至更高频率的信号 数字化后送入计算机处理: 3)由一维走向多维,像高分舞率彩色电视、雷达、石油勘探等多维信号处理的应用领域已与数 字信号处理结下了不解之缘 (4)各种数字信号处理系统均几经更新换代 在图像处理方面,图像数据压缩是多媒体通信、影碟机(VCD或DVD)和高清晰度电视(HDTV) 的关键技术。国际上先后制定的标准H261、PEG、MPEG一1和MPEG一2中均使用了离散余 弦变换(DCT)算法。近年来发展起来的小波(Wavelet)变换也是一种具有高压缩比和快速运算特点 的崭新压缩技术,应用前景十分广阔,可望成为新一代压缩技术的标准。 年代特点 S/MIPS 60年代 大学探索 S100-$1.000 70年代 军事运用 $10-S100 80年代 商用成功 51-$10 90年代 进入消费类电子 50.1-$1
3 二、数字信号处理的主要优点 数字信号处理采用数字系统完成信号处理的任务,它具有数字系统的一些共同优点,例如 抗干扰、可靠性强,便于大规模集成等。除此而外,与传统的模拟信号处理方法相比较,它还 具有以下一些明显的优点: 1、精度高 在模拟系统的电路中,元器件精度要达到 以上已经不容易了,而数字系统 17 位字长可 以达到 的精度,这是很平常的。例如,基于离散傅里叶变换的数字式频谱分析仪,其幅值 精度和频率分辨率均远远高于模拟频谱分析仪。 2、灵活性强 数字信号处理采用了专用或通用的数字系统,其性能取决于运算程序和乘法器的各系数, 这些均存储在数字系统中,只要改变运算程序或系数,即可改变系统的特性参数,比改变模拟 系统方便得多。 3、可以实现模拟系统很难达到的指标或特性 例如:有限长单位脉冲响应数字滤波器可以实现严格的线性相位; 在数字信号处理中可以将信号存储起来,用延迟的方法实现非因果系统,从而提高了系统的性 能指标; 数据压缩方法可以大大地减少信息传输中的信道容量。 4、可以实现多维信号处理 利用庞大的存储单元,可以存储二维的图像信号或多维的阵列信号,实现二维或多维的滤 波及谱分析等。 5、缺点 (1)增加了系统的复杂性。他需要模拟接口以及比较复杂的数字系统。 (2)应用的频率范围受到限制。主要是 A/D 转换的采样频率的限制。 (3)系统的功率消耗比较大。数字信号处理系统中集成了几十万甚至更多的晶体管,而模拟信 号处理系统中大量使用的是电阻、电容、电感等无源器件,随着系统的复杂性增加这一矛盾会 更加突出。 三、发展特点 (1)由简单的运算走向复杂的运算,目前几十位乘几十位的全并行乘法器可以在数个纳秒的时间 内完成一次浮点乘法运算,这无论在运算速度上和运算精度上均为复杂的数字信号处理算法提 供了先决条件; (2)由低频走向高频,模数转换器的采样频率已高达数百兆赫,可以将视频甚至更高频率的信号 数字化后送入计算机处理; (3)由一维走向多维,像高分辨率彩色电视、雷达、石油勘探等多维信号处理的应用领域已与数 字信号处理结下了不解之缘。 (4)各种数字信号处理系统均几经更新换代 在图像处理方面,图像数据压缩是多媒体通信、影碟机(VCD 或 DVD)和高清晰度电视(HDTV) 的关键技术。国际上先后制定的标准 H.261、JPEG、MPEG—1 和 MPEG—2 中均使用了离散余 弦变换(DCT)算法。近年来发展起来的小波(Wavelet)变换也是一种具有高压缩比和快速运算特点 的崭新压缩技术,应用前景十分广阔,可望成为新一代压缩技术的标准。 年代 特点 $/MIPS 60 年代 大学探索 $100-$1,000 70 年代 军事运用 $10-$100 80 年代 商用成功 $1-$10 90 年代 进入消费类电子 $0.1-$1

今后生活用品 S0.01-$0.1 四、各种数字信息系统 数字信号处理不断开辟新的应用领域 机 制造中,基于FT算法的频谱分析仪用于 动分析和机械故障诊断新:医学中使用 字信号处理技术对心电(ECG)和脑电(EEG)等生物电信号作分析和处理:数字音频广播(DAB)厂 泛地使用了数字信号处理技术。可以说,数字信号处理技术已在信总处理领域起 了广泛的关注和高度的面视。 五、数字信号处理系统的实现 牛实现 软件实现是用 一台通用的数字计算机运行数字信号处理程序。其优点是经济, 机可以多 用:缺点是处理速度慢,这是由于通用数字计算机的体系结构并不是为某一种特定算法而设 的。在许多非实时的应用场合,可以采用软件实现方法。例如,处理一盘混有噪声的录像(音) 带,我们可以将图像(声音)信号转换成数字信号并存入计算机,用较长的时间一帧锁地处理这 些数据。处理完毕后,再实时地将处理结果还原成一盘清晰的录像(音)带。通用计算机即可完 成上述任务,而不必花费较大的代价去设 一台专用数字计算机。 硬件实现 硬件实现是针对特定的应用目标,经优化,设计一专用的软硬件系统。其优点是容易做到 实时处理,缺点是设备只能专用。 ·片上系统(SOC,System on a Chip) 大规模集成 电路日 个复 数字信号处理系统己可以集成在一个芯片上。SO( 包含有数字和模拟电路、模拟和数字转换电路、微处理器、微控制器以及数字信号处理器等 与传统的集成电路不同的是,嵌入式软件的设计也被集成到了SOC的设计流程中,SOC的设计 方法将以组装为基础,采用自上至下的设计方法,在设计过程中大量重复使用自行设计或其他 第三方拥有知识产权的POIntelligent property)模块。SOC要充分考虑如何合理别分软件和硬件 所实现的系统功能以及如何实现软、硬件之间的信息传递。SOC将是数字信号处理系统的 新型的实现方沙 并行、复用和流水 并行是指为了完成同一个任务,几个处理器同时工作,使系统能胜任单个处理器所不能完 成的任务:当一个处理器完成单个任务(比如一个滤波器)有很大的富余量时,可让其完成多个 任务,这就是复用:流水结构也是多处理器完成同一任务,它与并行结构的主要区别在于并行 的各个处理器之间数据交换不多,而流水结构类似于生产中的流水线,数据经一道道“工序” 理。采用并行或流水结构,完全取决于数字信号处理的运算结构。 研究内容 经典的数字信号处理限于线性时不变系统理论,数字滤波和FT是常用方法 目前Dp研究执占. 时变非线性系统、非平稳信号、非高斯信号 处理方法的发展:自适应滤波 离散小波变换 高阶矩分析、盲处理、分形、混沌理论 课程介绍 基础理论:离散时间信号与系统(第一章) 离散傅立叶变换DFT及其快速算法FFT (第三章)》 无限长单位脉冲响应(R)滤波器(第四章) 有限长单位脉冲响应(FIR)滤波器(第五章)
4 今后 生活用品 $0.01-$0.1 四、各种数字信息系统 数字信号处理不断开辟新的应用领域 在机械制造中,基于 FFT 算法的频谱分析仪用于振动分析和机械故障诊断;医学中使用数 字信号处理技术对心电(ECG)和脑电(EEG)等生物电信号作分析和处理;数字音频广播(DAB)广 泛地使用了数字信号处理技术。可以说,数字信号处理技术已在信息处理领域引起 了广泛的关注和高度的重视。 五、数字信号处理系统的实现 • 软件实现 软件实现是用一台通用的数字计算机运行数字信号处理程序。其优点是经济,一机可以多 用;缺点是处理速度慢,这是由于通用数字计算机的体系结构并不是为某一种特定算法而设计 的。在许多非实时的应用场合,可以采用软件实现方法。例如,处理一盘混有噪声的录像(音) 带,我们可以将图像(声音)信号转换成数字信号并存入计算机,用较长的时间一帧帧地处理这 些数据。处理完毕后,再实时地将处理结果还原成一盘清晰的录像(音)带。通用计算机即可完 成上述任务,而不必花费较大的代价去设计一台专用数字计算机。 • 硬件实现 硬件实现是针对特定的应用目标,经优化,设计一专用的软硬件系统。其优点是容易做到 实时处理,缺点是设备只能专用。 • 片上系统(SOC, System on a Chip) 随着大规模集成电路的发展,一个复杂数字信号处理系统已可以集成在一个芯片上。SOC 包含有数字和模拟电路、模拟和数字转换电路、微处理器、微控制器以及数字信号处理器等。 与传统的集成电路不同的是,嵌入式软件的设计也被集成到了 SOC 的设计流程中,SOC 的设计 方法将以组装为基础,采用自上至下的设计方法,在设计过程中大量重复使用自行设计或其他 第三方拥有知识产权的 IP(Intelligent Property)模块。SOC 要充分考虑如何合理划分软件和硬件 所实现的系统功能以及如何实现软、硬件之间的信息传递。SOC 将是数字信号处理系统的一个 新型的实现方法。 并行、复用和流水 并行是指为了完成同一个任务,几个处理器同时工作,使系统能胜任单个处理器所不能完 成的任务;当一个处理器完成单个任务(比如一个滤波器)有很大的富余量时,可让其完成多个 任务,这就是复用;流水结构也是多处理器完成同一任务,它与并行结构的主要区别在于并行 的各个处理器之间数据交换不多,而流水结构类似于生产中的流水线,数据经一道道“工序”处 理。采用并行或流水结构,完全取决于数字信号处理的运算结构。 研究内容 经典的数字信号处理限于线性时不变系统理论, 数字滤波和 FFT 是常用方法。 目前 DSP 研究热点: 时变非线性系统、非平稳信号、 非高斯信号 处理方法的发展:自适应滤波、 离散小波变换、 高阶矩分析、盲处理、分形、混沌理论 课程介绍 基础理论:离散时间信号与系统(第一章) Z 变换(第一章) 离散傅立叶变换 DFT 及其快速算法 FFT (第三章) 无限长单位脉冲响应(IIR)滤波器(第四章) 有限长单位脉冲响应(FIR)滤波器(第五章)
第一章第一节内容: 第一章离散时间信号 ·离散时间信号 ·线性移不变系统 ·常系数线性差分方程 ·连续时间信号的抽样 学习要求:热练学提和运用采样定理提离散时间信号与系统的定义:会判定系统的因果性 和稳定性。 1.1离散时间信号 一、主要常用序列 (1)单位脉冲序列 n=0 1 n≠0 (2)单位阶跃序列 1 n≥0 n<0 n (3)矩形序列 rm-0, 1, 0≤n≤N-1 n<0,n≥N -3-2-101. (4)实指数序列 an≥0 x(n)=a"u(n) (a) (5)正弦序列 x(m)=sin (moip 注意:正弦型序列不一定是周期序列 (6)复指数序列
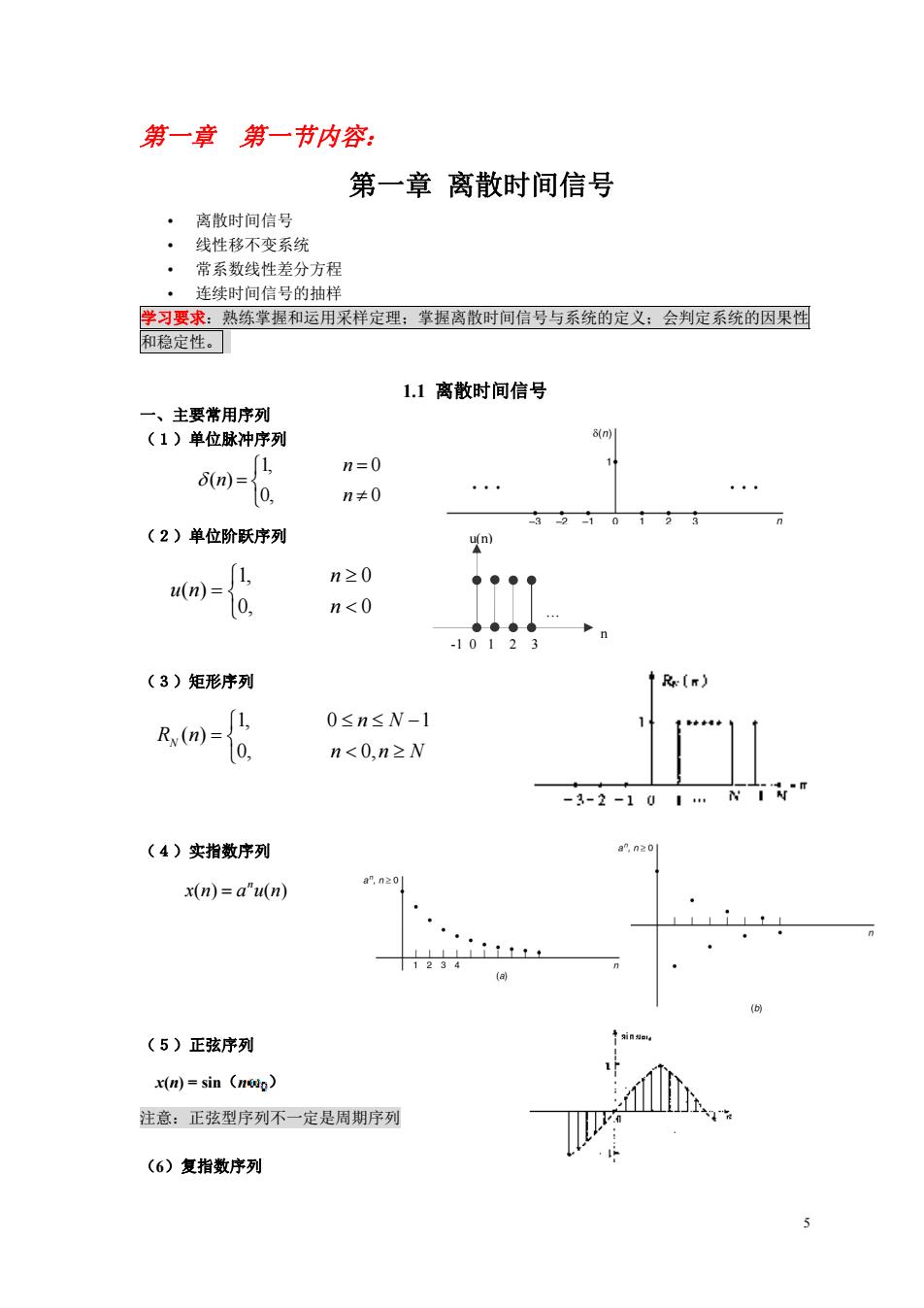
5 第一章 第一节内容: 第一章 离散时间信号 • 离散时间信号 • 线性移不变系统 • 常系数线性差分方程 • 连续时间信号的抽样 学习要求:熟练掌握和运用采样定理;掌握离散时间信号与系统的定义;会判定系统的因果性 和稳定性。 1.1 离散时间信号 一、主要常用序列 (1)单位脉冲序列 (2)单位阶跃序列 (3)矩形序列 (4)实指数序列 (5)正弦序列 x(n) = sin(n ) 注意:正弦型序列不一定是周期序列 (6)复指数序列 0, 0 1, 0 ( ) n n n 0, 0 1, 0 ( ) n n u n . -1 01 2 3 n u(n) n n N n N R n N 0, 0, 1, 0 1 ( ) 1 . N-1 x(n) a u(n) n

x(n)=Ae=Ae"(cosan+jsinn) 当a=0时n)的实部和虚部,分别是余弦和正弦序列, 二、序列的运算 1、序列的移位)=x-m当m为正时,x(-m)表示依次右移m位: x(叶m)表示依次左移m位。 2、序列的相加m=xm+n)是指同序号n的序列值逐项对应相加得一新序列。 3、序列的相乘 m))是指同序号()的序列值逐项对应相乘 4、序列的翻 如果有xO,则n是以n0为对称轴将x)加以翻的序列 5、序列的累加 =∑x)表示n以前的所有x()的和。 6、前向差分和后向差分 △x(m)=x(n+1)一x(m)(先左移后相减):7x(m=x(n)-x(n-1)(先右移后相减) 7、序列的尺度变换 抽取:x →xm,m为正整数插值:x创 →xm,m为正整数 101 图1序列xm)及超前序列x+) 8-101 图15序列x)及其累加序列ym) ar(a) 01 图1-2两序列相如 图13序列xn)及翻裙后的序列x(m c(u 2-1012 (a) (b) 图1-7某序列及其抽取序列 8、序列的卷积和 6
6 当 时 x(n)的实部和虚部,分别是余弦和正弦序列。 二、序列的运算 1、序列的移位 y(n)=x(n-m) 当 m 为正时,x(n-m)表示依次右移 m 位; x(n+m)表示依次左移 m 位。 2、序列的相加 z(n)=x(n)+y(n)是指同序号 n 的序列值逐项对应相加得一新序列。 3、序列的相乘 f(n)=x(n) y(n) 是指同序号(n)的序列值逐项对应相乘。 4、序列的翻褶 如果有 x(n),则 x(-n)是以 n=0 为对称轴将 x(n)加以翻褶的序列。 5、序列的累加 表示 n 以前的所有 x(n)的和。 6、前向差分和后向差分 (先左移后相减); (先右移后相减) 7、序列的尺度变换 抽取:x(n) x(mn), m 为正整数; 插值: x(n) x(n/m), m 为正整数。 图 1-1 序列 x(n)及超前序列 x(n+1) 图 1-5 序列 x(n)及其累加序列 y(n) 图 1-2 两序列相加 图 1-3 序列 x(n)及翻褶后的序列 x(-n) 图 1-7 某序列及其抽取序列 8、序列的卷积和 0 ( ) 0 0 ( ) (cos sin ) j n n x n Ae Ae n j n 0 n k y(n) x(k) x(n) x(n 1) x(n) x(n) x(n) x(n 1)

设序列xn,hn,它们的卷积和ym)定义为 m)=∑xmhn-m)=2hmxn-m=xn*hm 卷积和计算分四步:折选(翻榴,位移,相乘,相加。 1 012 h(一1一知】 -3-2-1】 4(1-m) -+1>0右愁 1.1瓶 -1012145m 图1-8X和h(n)的卷积和图解 三、序列的周期性 存在 一个最小的正整数N,满足Fx(+N,则序列()为周期性序列,N为周期。 四、用单位抽样序列表示任意序列 1、任意序列可表示成单位抽样序列的位移加权和. m=工m6a-m 2.、n)亦可看成n)和8(n)的卷积和 五、序列的能量 xm)的能量定义为 E=∑lnf 第一章第二节内容: 1-2 线性移不变系统 一、 线性系统 系统实际上表示对输入信号的一种运算,所以离散时间系统就表示对输入序列的运算,即 y(n)=T[x(n)] n人 离散时间系统 T[z(n)] 线性系统具有均匀性和迭加性 y (n)=T[x(n)]y2 (n)=T[x(m)] Tlax(n)+a.x:(n)]=aT(n)]+aTx:(n)] 加权信号和的响应=响应的加权和。 *先运算后系统操作=先系统操作后运算。 二、移不变系统 如Tx(Fy,则Tx(n-m-y(-m),满足这样性质的系统称作移不变系统。 即系统参数不随时间变化的系统,亦即输出波形不随输入加入的时间而变化的系统
7 x(n) 离散时间系统 T[x(n)] y(n) 设序列 x(n), h(n), 它们的卷积和 y(n)定义为 卷积和计算分四步:折迭(翻褶), 位移, 相乘, 相加。 图 1-8 x(n)和 h(n)的卷积和图解 三、序列的周期性 如果存在一个最小的正整数 N, 满足 x(n)=x(n+N), 则序列 x(n)为周期性序列, N 为周期。 四、用单位抽样序列表示任意序列 1、任意序列可表示成单位抽样序列的位移加权和. 2.、x(n)亦可看成 x(n)和δ(n)的卷积和 五、序列的能量 x(n)的能量定义为 第一章 第二节内容: 1-2 线性移不变系统 一、线性系统 系统实际上表示对输入信号的一种运算,所以离散时间系统就表示对输入序列的运算,即 线性系统具有均匀性和迭加性: *加权信号和的响应=响应的加权和。 *先运算后系统操作=先系统操作后运算。 二、移不变系统 如 T[x(n)]=y(n),则 T[x(n-m)]=y(n-m), 满足这样性质的系统称作移不变系统。 即系统参数不随时间变化的系统,亦即输出波形不随输入加入的时间而变化的系统。 y(n)=T[x(n)] m m y(n) x(m)h(n m) h(m)x(n m) x(n) h(n) m x(n) x(m) (n m) n E x n 2 ( ) ( ) ( ) ( ) ( ) , ( ) ( ) , ( ) ( ) , 1 1 2 2 1 1 2 2 1 1 2 2 T a x n a x n a T x n a T x n y n T x n y n T x n

y(n)x(m)sin(2。+)不是移不变 *系统操作=函数操作 三、单位抽样响应与卷积利 第一章第三节内容: 四线性移不变系统的性质 1.交换律(n)=x(m)*h(m)=m)*x(m) 2.结合律 x(m)*h()*h,(m)=[x()*h(n]*2(n) =[(n)*h(n*h(m) =x(n)*[h,(m)*h(n] 3.对加法的分配律x(m)*[h,(n)+h(n =x(n)*h,(n)+x(n)*h(n) 五因果系统 某时刻的输出只取决于此刻以及以前时刻的输入的系统称作因果系统。 *实际系统一般是因果系统 *对图象、己记录数据处理以及平均处理的系统不是因果系统 *y(nFx-n)是非因果系统,因0时的输入: 线性移不变因果系统的充要条件为h(n=0,n<0。 六稳定系统 有界的输入产生有界的输出系统。 线性移不变稳定系统的充要条件是 ∑h(n=p< 第一章第四节内容 1-3常系数线性差分方程 离散变量n的函数n)及其位移函数xn-m)线性叠加而构成的方程 一表示法与解法 1.表示法 a0n-k)=26xn-m 幸常系数:al.al. :b0b.bM均是常数(不含n 阶数:y)变量n的最大序号与最小序号之差 如N=N0 ◆线性:yn-k),x血-m)各项只有一次幂,不含它们的乘积项。 2.解法 时域:迭代法,卷积和法
8 *系统操作=函数操作 三、单位抽样响应与卷积和 第一章 第三节内容: 四.线性移不变系统的性质 1.交换律 2.结合律 3.对加法的分配律 五.因果系统 某时刻的输出只取决于此刻以及以前时刻的输入的系统称作因果系统。 *实际系统一般是因果系统; *对图象、已记录数据处理以及平均处理的系统不是因果系统; * y(n)=x(-n)是非因果系统, 因 n0 时的输入; 线性移不变因果系统的充要条件为 h(n)=0,n< 0。 六.稳定系统 有界的输入产生有界的输出系统。 线性移不变稳定系统的充要条件是 第一章 第四节内容: 1-3 常系数线性差分方程 离散变量 n 的函数 x(n)及其位移函数 x(n-m)线性叠加而构成的方程. 一.表示法与解法 1.表示法 * 常系数:a0,a1,.,aN ; b0,b1,.,bM 均是常数(不含 n). *阶数:y(n)变量 n 的最大序号与最小序号之差 ,如 N=N-0. *线性:y(n-k), x(n-m)各项只有一次幂,不含它们的乘积项。 2.解法 时域:迭代法,卷积和法; 2 ( ) ( ) sin ( ) 9 7 yn xn n 不是移不变 y(n) x(n)h(n) h(n) x(n) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 2 2 1 1 2 1 2 x n h n h n x n h n h n x n h n h n x n h n h n ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 2 1 2 x n h n x n h n x n h n h n n h(n) p N k M m ak y n k bm x n m 0 0 ( ) ( )

变换域:Z变换法 二用迭代法求解差分方程 1.“松驰”系统的输出 起始状态为零的系统 ,这种系统用的较多,其输出就是y()=x(m)*hn) 因此,已知h(n)就可求出y(n),所以必须知道h(n)的求法. 2.迭代法(以求h(n)为例) 例:已知常系数线性差分方程为yn-yn-l)=n),试求单位抽样响应h(n) 解:因果系统有hn=0,n<0; 方程可写作:y=yn-1)+xm) in)=muin-D+rin) hm)=a".n20 1=ah0)+1=a-1+0=d 0.n<0 2) )=a2+0= 注意: <是稳定系统 1。一个常系数线性差分方程架二代表茵架泰矣,采一定表示线性移不变系统。这些都由 边界条件(初始)所决定。 2我们讨论的系统都假定:常系数线性差分方程就代表线性移不变系统,且多数代表因果系统 二系统结构 1系统的输入与输出的运算关系的表述方法 2.差分方程可直接得到系统结构。 例:y(n)=b0x(n)-alyn-l1) 用⊕表示相加器: 用☒表示乘法器 用Z表示 一位延时单元 例:差分方程yn=b0xaly-l)表示的系统结构为: 《m》。 y。 1-4连续时间信号的抽样 一抽样器与抽样 1.抽样器 0一 ()器的原 2.抽样 对信号进行时间上的量化, . 这是对信号作数字化处理的 一个环节。 p) 11 4 =月 ilm. b)实精号
9 变换域:Z 变换法. 二.用迭代法求解差分方程 1.“松弛”系统的输出 起始状态为零的系统,这种系统用的较多,其输出就是 。 因此,已知 h(n)就可求出 y(n),所以必须知道 h(n)的求法. 2.迭代法(以求 h(n)为例) 例: 已知常系数线性差分方程为 y(n)-ay(n-1)=x(n),试求单位抽样响应 h(n). 解:因果系统有 h(n)=0,n<0 ; 方程可写作: y(n)=ay(n-1)+x(n) 注意: 1.一个常系数线性差分方程并不一定代表因果系统,也不一定表示线性移不变系统。这些都由 边界条件(初始)所决定。 2.我们讨论的系统都假定:常系数线性差分方程就代表线性移不变系统,且多数代表因果系统。 三.系统结构 1.系统的输入与输出的运算关系的表述方法。 2.差分方程可直接得到系统结构。 例:y(n)=b0x(n)-a1y(n-1) 用⊕表示相加器; 用 表示乘法器; 用 表示一位延时单元。 例:差分方程 y(n)= b0 x(n)-a1y(n-1)表示的系统结构为: 1-4 连续时间信号的抽样 一.抽样器与抽样 1.抽样器 2. 抽样 对信号进行时间上的量化, 这是对信号作数字化处理的 第一个环节。 y(n) x(n)h(n) n n h n ah n n a a h ah a a h ah a a h ah h n ah n n x n n y n h n y n ay n x n ( ) ( 1) ( ) 0 (2) (1) (2) 0 (1) (0) (1) 1 0 (0) ( 1) (0) 0 1 1 ( ) ( 1) ( ), ( ) ( ), ( ) ( ), ( ) ( 1) ( ), 2 2 因此 当 故 0, 0 , 0 ( ) n a n h n n a 1是稳定系统 1 Z T fs 1

问题: ·信号经采样后发生的变化(如频谱的变化): ·信号内容是否丢失(采样序列能否代表原始信号、如何不失真地还原信号): 抽样与理想抽样 实际抽样 p为脉冲序列 般由电开关组成,开关每隔T秒短暂地闭合一次,将连续信号接通,实现 一次采样 次闭合T秒 米蒂的御出是一甲 ,宽度为工的 脉 的隔 期为、宽度为:的E形脉冲。 出为 制信号是输入的连续信号x),则采样 :很小,越小,采样输出脉冲的幅度越接近输入信号在离散时间点上的瞬时值。 理想抽样:p()=6,()(冲激序列) 当抽样器的电开关闭合时间τ→0时,为理想采样。 采样序列表示为冲激函数的序列,这些冲激函数准确地出现在采样瞬间,其积分幅度准确地等 于输入信号在采样瞬间的幅度,即:理想采样可看作是对冲激脉冲载波的调幅过程。 示 M9=∑0-力 则有理想采样信号可表示为:元)=元,付M0=立x8(t-m=立x,8t-m 说明:实际情况下,t=0达不到,但K<T时,实际采样接近理想采样,理想采样可看作是实 际采样物理过程的抽象,便于数学描述,可集中反映采样过程的所有本质特性,理想采样对Z 变换分析相当重要 3采样信号的频谱 1)频谱延拓 问题:理想采样信号的频谱有何特点,它与连续信号频谱的关系? .U0=号x.Un-mm) 其中 心为理想采样信号的频谱, X网为连续信号的付氏变换。显然,元.(是频率 Q的连续函数。 xn) (8) x(n) 10
10 问题: 信号经采样后发生的变化(如频谱的变化); 信号内容是否丢失(采样序列能否代表原始信号、如何不失真地还原信号); 由离散信号恢复连续信号的条件? 2.实际抽样与理想抽样 实际抽样: p(t)为脉冲序列 抽样器一般由电开关组成,开关每隔T秒短暂地闭合一次,将连续信号接通,实现一次采样。 如开关每次闭合τ秒,则采样器的输出是一串重复周期为 T,宽度为τ的脉冲,脉冲的幅度是 这段时间内信号的幅度,如图 1.1(d),这一采样过程可看作是一个脉冲调幅过程,脉冲载波是 一串周期为 T、宽度为τ的矩形脉冲,以 P(t)表示,调制信号是输入的连续信号 xa(t),则采样输 出为 Xp(t)=Xa(t)P(t) 一般τ很小, τ越小,采样输出脉冲的幅度越接近输入信号在离散时间点上的瞬时值。 理想抽样: (冲激序列) 当抽样器的电开关闭合时间 τ→0 时,为理想采样。 采样序列表示为冲激函数的序列,这些冲激函数准确地出现在采样瞬间,其积分幅度准确地等 于输入信号在采样瞬间的幅度,即:理想采样可看作是对冲激脉冲载波的调幅过程。 理想采样信号的数学表示: 用 M(t)表示冲击载波, 则有理想采样信号可表示为: 说明:实际情况下,τ=0 达不到,但 τ<<T 时,实际采样接近理想采样,理想采样可看作是实 际采样物理过程的抽象,便于数学描述,可集中反映采样过程的所有本质特性,理想采样对 Z 变换分析相当重要。 3.采样信号的频谱 1)频谱延拓 问题:理想采样信号的频谱有何特点,它与连续信号频谱的关系? 对理想采样信号进行傅立叶变换,可以证明,理想采样信号的频谱是连续信号频谱的周期延拓, 重复周期为 s(采样频率),即 其中 为理想采样信号的频谱, 为连续信号的付氏变换。显然, 是频率 Ω的连续函数。 p(t) (t) T