
/JIANG UNIVERSK 第3章 离散傅里叶变换及其 快速算法
第3章 离散傅里叶变换及其 快速算法

内容概要 3.1离散傅立叶变换 3.2利用DFT进行连续信号的频谱分析 3.3快速傅立叶变换 3.4关于FFT应用中的几个问题 2
内容概要 2 3.4关于FFT应用中的几个问题 3.3快速傅立叶变换 3.2利用DFT进行连续信号的频谱分析 3.1离散傅立叶变换
理解和熟悉离散傅立叶变换及其 性质 掌握利用DFT进行连续信号频谱 分析 第3章 素 掌握快速傅立叶变换算法的原理 3 及有关FFT的一些问题 3
3 教学 目标 第3章 理解和熟悉离散傅立叶变换及其 1 性质 掌握利用DFT进行连续信号频谱 2 分析 掌握快速傅立叶变换算法的原理 3 及有关FFT的一些问题

引言 离散傅里叶变换不仅具有明确的物理意义, 相对于DTFT他更便于用计算机处理。但是,直至上 个世纪六十年代,由于数字计算机的处理速度较低 以及离散傅里叶变换的计算量较大,离散傅里叶变 换长期得不到真正的应用。 >快速离散傅里叶变换算法的提出,才得以显现 出离散傅里叶变换的强大功能,并被广泛地应用于 各种数字信号处理系统中。 >近年来,计算机的处理速率有了惊人的发展, 同时在数字信号处理领域出现了许多新的方法,但 在许多应用中始终无法替代离散傅里叶变换及其快 速算法
➢ 离散傅里叶变换不仅具有明确的物理意义, 相对于DTFT他更便于用计算机处理。但是,直至上 个世纪六十年代,由于数字计算机的处理速度较低 以及离散傅里叶变换的计算量较大,离散傅里叶变 换长期得不到真正的应用。 ➢ 快速离散傅里叶变换算法的提出,才得以显现 出离散傅里叶变换的强大功能,并被广泛地应用于 各种数字信号处理系统中。 ➢ 近年来,计算机的处理速率有了惊人的发展, 同时在数字信号处理领域出现了许多新的方法,但 在许多应用中始终无法替代离散傅里叶变换及其快 速算法。 引言

本章主要内容 *离散傅里叶变换 *利用DFT进行连续信号的频谱分析 *快速傅里叶变换 *FFT应用
离散傅里叶变换 利用DFT进行连续信号的频谱分析 快速傅里叶变换 FFT应用 本章主要内容

3.1离散傅里叶变换(DFT) 为了便于更好地理解DFT的概念,先讨论周期序列及其 离散傅里叶级数(DFS)表示。 §2.1.1离散傅里叶级数(DFS) 一个周期为N的周期序列,即 X(n)=X(n kN) k为任意整数,N为周期 周期序列不能进行Z变换,因为其在n=-0到+0都周 而复始永不衰减,即z平面上没有收敛域。但是,正象 连续时间周期信号可用傅氏级数表达,周期序列也可用离 散的傅氏级数来表示,也即用周期为N的正弦序列来表示
3.1 离散傅里叶变换(DFT) 为了便于更好地理解DFT的概念,先讨论周期序列及其 离散傅里叶级数(DFS)表示。 §2.1.1 离散傅里叶级数(DFS) 一个周期为N的周期序列,即 k为任意整数,N为周期 周期序列不能进行Z变换,因为其在 n=-到+ 都周 而复始永不衰减,即 z 平面上没有收敛域。但是,正象 连续时间周期信号可用傅氏级数表达,周期序列也可用离 散的傅氏级数来表示,也即用周期为N的正弦序列来表示

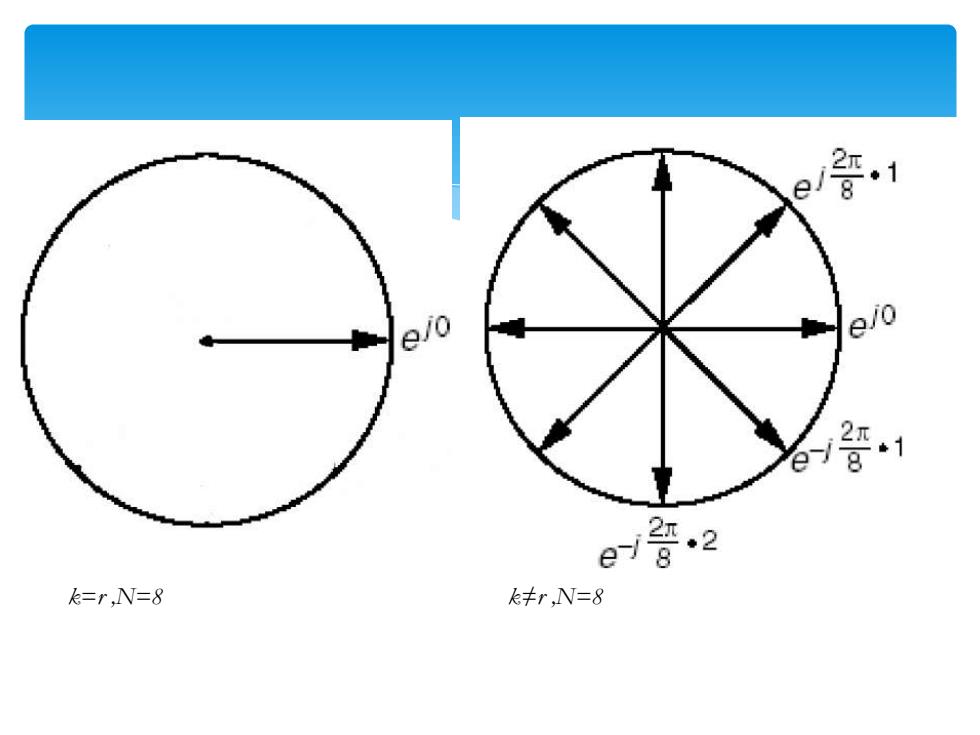
周期为N的正弦序列其基频成分为: e((an)=e2π/w)m 饮谐波序列为: ek(n)=eJ(2π/Nkm 但离散级数所有谐波成分中只有个是独立的,这是与连续傅 氏级数的不同之处, eba/Nk+a)=e2x/m 即 因此 ekiN (n)=ex(n) 192 XINJIANG UNIVERSIT
但离散级数所有谐波成分中只有N个是独立的,这是与连续傅 氏级数的不同之处, 即 因此 周期为N的正弦序列其基频成分为: K次谐波序列为:
2.1 /0 a/0 2π」 1 e2 k=r,N=8 k≠r,N=8
k=r ,N=8 k≠r ,N=8

将周期序列展成离散傅里叶级数时,只需取k0 到(-)这N个独立的谐波分量,所以一个周期序列 的离散傅里叶级数只需包含这N个复指数, 0=∑rWec地 NK=0 利用正弦序列的周期性可求解系数 X() 将上式两边乘e2wm,并对一个周期求和:
将周期序列展成离散傅里叶级数时,只需取 k=0 到(N-1) 这N个独立的谐波分量,所以一个周期序列 的离散傅里叶级数只需包含这N个复指数, 利用正弦序列的周期性可求解系数 。 将上式两边乘 ,并对一个周期求和:

N 2π 1V-1W-1 ∑m)e 2k-0r 2k-加 x∑e n=0 n=0k=0 n=0 哈 k=0 2π N n=0 0k-r≠sW