1.用留数定理求逆Z变换 m=2Xet-2eKer八小 为C内的第k个极点, 个jmlz] Res[X(z)z",=] Re[z] 表示极点处的留数。 R
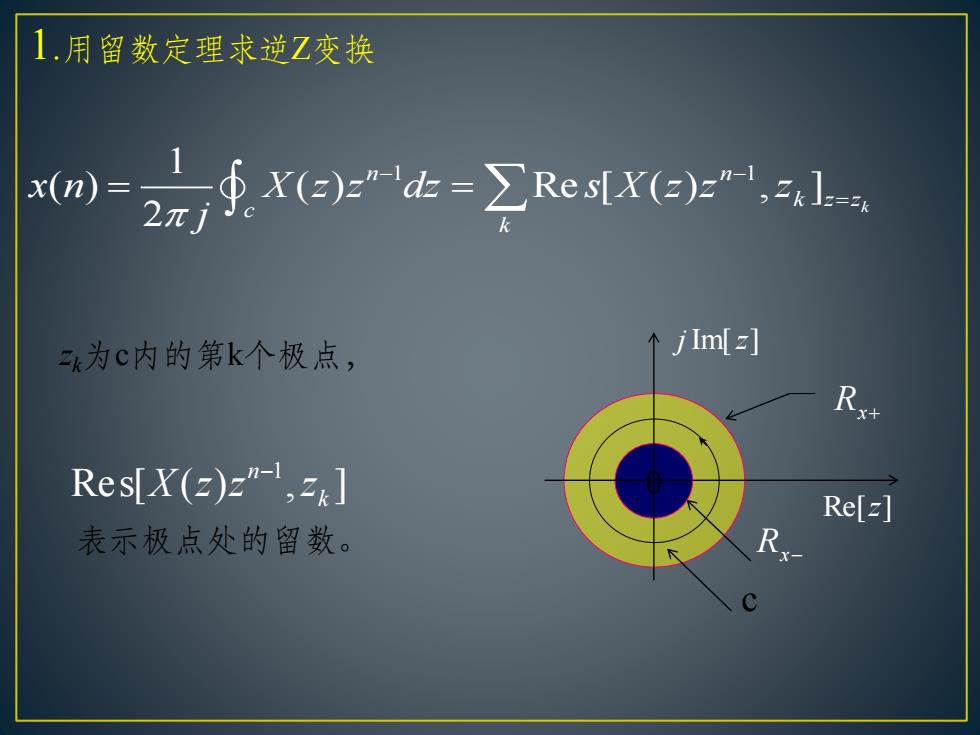
1.用留数定理求逆Z变换 1 1 1 ( ) ( ) Re [ ( ) , ] 2 k n n k z z c k x n X z z dz s X z z z j − − = = = zk为c内的第k个极点, j Im[z] Re[z] Rx− Rx+ 0 c 表示极点处的留数。 1 Res[ ( ) , ] n X z z zk −

留数的求法: (1)当Z为一阶极点时的留数: Res[X()J=(=-=)X()= (2)当Z为N阶(s重)极点时的留数: e4-rxeE儿 为C内的极点,=1,2,N1 m为c外的极点,m=1,2.,N2 因为eXel=-立Ree】 k=1 m=] 我们可根据计算方便任意选取围线内外的留数进行计算
(2) 当Zk为N阶(s重)极点时的留数: 1 1 1 1 1 Re [ ( ) , ] [( ) ( ) ] ( 1)! k s n s n k r s z z d s X z z z z z X z z s dz − − − − = = − − 留数的求法: (1)当Zr为一阶极点时的留数: 1 1 Re [ ( ) ] ( , ) ( ) k n n k r z z s X z z z z z X z z − − = = − zk为c内的极点,k=1,2, ∙∙∙,N1 zm为c外的极点,m=1,2, ∙∙∙,N2 1 2 1 1 1 1 Re [ ( ) , ] Re [ ( ) , ] N N n n k m k m s X z z z s X z z z − − = = 因为: = − 我们可根据计算方便任意选取围线内外的留数进行计算

例已知X(2)= -E小>a 求其逆Z变换。 z” +Im[z] 解:令F(z)=X(z)z"-1= 即F(z)= 1-az z-a a Re[z] 当n≥0时,因为z>a,围线c内F(z)有一个 单阶极点z=a,围线c外有一个阶极点z=o x)-Re()-l-ReF().al-(-a) =a -a 当nRes[F(),=]=->Res[F(=).=]=0 n≥0 因此:x(n)= 即:x(n=a"u(n) 0 n<0
1 1 ( ) , z 1 X z a Z az − = − 例 已知 ,求其逆 变换。 1 1 1 ( ) ( ) ( ) 1 n n n z z F z X z z F z az z a − − − = = = − − 解:令 ,即 0 ( ) , n z a c F z z a c n z = = 当 时,因为 ,围线 内 有一个 单阶极点 围线 外有一个 阶极点 1 1 1 ( ) Re [ ( ) , ] Re [ ( ), ] ( ) n n n k k z a z x n s X z z z s F z a z a a z a − = = = = = − = − 0 ( ) , 0; n z n c F z z a z a n z c = = − = 当 时,围线 内 有一个单阶极点 和一个 阶极点 围线 没有极点,故: ( ) Re [ ( ), ] Re [ ( ), ] 0 k m k m x n s F z z s F z z = = − = 0 ( ) ( ) ( ) 0 0 n a n n x n x n a u n n = = 因此: 即: a Im[z] 0 Re[z] 1 C

例已知X(z)= -rX1-ea1,求其道Z变换Um 1-a 解:Fe)=Xe)= (1-a2)zr (1-a2)z" (1-ar)1-ae)-a(z-a(z-a') 由于本题没给收敛域,必须考虑所有情况 Im[z] ()收敛域>a,围线外无极点为右边序列, 即n≥0,围线内有两个单阶极点三1=a,22=a Re[z] 0 合打 xm)=∑ResF(el k=1 (1-a2)z” (1-a2)z" =a”-am(n≥0) 即:x(n)=(a”-a")u(n)
2 1 1 ( ) , ( ) (1 )(1 ) a X z a Z x n az az − − = − − 例 已知 <1,求其逆 变换 。 2 1 2 1 1 1 (1 ) (1 ) ( ) ( ) (1 )(1 ) ( )( ) n n n a z a z F z X z z az az a z a z a − − − − − − = = = − − − − − 解: 1 1 1 2 (1) , 0 , z a n z a z a − − = = 收敛域 围线外无极点为右边序列, 即 ,围线内有两个单阶极点 由于本题没给收敛域,必须考虑所有情况 a 1 a − Im[z] Re[z] 0 c 1 2 1 2 2 1 1 1 ( ) Re [ ( ), ] (1 ) (1 ) ( ) ( ) ( )( ) ( )( ) ( 0) k k n n z a z a n n x n s F z z a z a z z a z a a z a z a a z a z a a a n − = − − − = = − = − − = − + − − − − − − − = − ( ) ( ) ( ) n n x n a a u n − 即: = −

(2)收敛域<ad ↑Im[z 围线外有两个单阶极点z2=a,二?=a, 当n<0时,围线内一个n阶极点为z,=0, Re[z] _1 x(n)=Res[F(),=] =-∑Res[F(z,] k=2 -40-0。儿 1-a2)z” =-a”+am (n<0) 即:x(n)=(a”-ad")u(-n-1)
a 1 a − Im[z] Re[z] 0 c 1 2 3 1 (2) , , 0 0 z a z a z a n n z − = = = 收敛域 围线外有两个单阶极点 当 时,围线内一个 阶极点为 , 1 1 3 2 2 2 1 1 1 ( ) Re [ ( ), ] Re [ ( ), ] (1 ) (1 ) ( ) ( ) ( )( ) ( )( ) ( 0) k k n n z a z a n n x n s F z z s F z z a z a z z a z a a z a z a a z a z a a a n − = − − − = = − = = − − = − − − − − − − − − − = − + - ( ) ( ) ( 1) n n x n a a u n − 即: = − − −

3)收致域a<<a 当n<0时, 4m[z] 围线内有阶极点z=0、单阶极点z2=a Re[z] 围线外有一个单阶极点三,=a, x(n)=-Res[F(z),a] (1-a2)z” -ae-aje-ar-a'=a” (n<0) 当n≥0时,围线内有单阶极点z,=a x(n)=Res[F(z),a] ale-aeae-a以=a (1-a2)z” (n≥0) 因此:x(n)= a” n≥0 a n n<0
1 a − Re[z] Im[z] 0 c a 1 1 2 1 3 (3) 0 0 , a z a n n z z a z a − − = = = 收敛域 当 时, 围线内有 阶极点 、单阶极点 围线外有一个单阶极点 1 1 2 1 1 ( ) Re [ ( ), ] (1 ) ( ) ( 0) ( )( ) n n z a x n s F z a a z z a a n a z a z a − − − − − = = − = − − = − − − - 2 当 时,围线内有单阶极点 n z a = 0 2 1 ( ) Re [ ( ), ] (1 ) ( ) ( 0) ( )( ) n n z a x n s F z a a z z a a n a z a z a − = = − = − = − − − 0 ( ) 0 n n a n x n a n − = 因此: