
筑结构学报 蕴老第9期20品月0 文章编号:100 D0:10.14006/-jg.2017.09.0 基于能量耗散的混凝土塑性损伤模型 龙洽川2.径鉴操3.王玉山 (1.重庆大学山地拔镇建设与新技术教有部重点实验室,重庆400045:2.重庆大学土木工程学院,重庆400045: 3.石河子大学水利建筑工程学院,新程石河子832000) 摘要:应用连续介质损伤力学和性流动理论,建立了基于能量耗散机制的型性损伤帮合烦型,型采用非关联理性流动 ,葛于有限元程序ABA0S,推导了增量格式的材料准可比矩阵,构建了型性 伤模型的仿直分析程序。 受压士抗压强度 准确模拟损伤导致的件获的构件响应与试验结果 文献标伤模型:仿真模 A plastic-damage model of concrete based on energy-oss mechanism HOU Jia G Yu model was develop by using entia cepls o n damage evoluti tion of damage vanal stiffness degru ution was given in s of the and accumul calculaled according lo the stress c strain rela s model wa implemented into ABAQUS the derivation of Jacobian matrix of material in rate form This model was used to analyze biaxial compressive test of concrete slab,three-point-oading notched beam test and flexural test of reinforced concrete beam.Numerical results agree well with those obtained from tests.It is concluded that the plastic-damage model can represent the effects of multi-nxial loading state on the compressive strength and simulate the nonlinea structural response due to damage Keywords:concrete:damage mechanics:plastie mechanics:plastie-damage model:numerical simulation 日精:2016年7月 147 1994-20 7China Academic Joumal Electronie Publishing House.All rights reserved. http://www.cnki.net
建筑结构学报 Journal of Building Structures 第 38 卷 第 9 期 2017 年 9 月 Vol. 38 No. 9 Sep. 2017 017 文章编号: 1000-6869( 2017) 09-0147-07 DOI: 10. 14006 /j. jzjgxb. 2017. 09. 017 基于能量耗散的混凝土塑性-损伤模型 龙渝川1,2 ,侯鉴珊2 ,王玉山3 ( 1. 重庆大学 山地城镇建设与新技术教育部重点实验室,重庆 400045; 2. 重庆大学 土木工程学院,重庆 400045; 3. 石河子大学 水利建筑工程学院,新疆石河子 832000) 摘要: 应用连续介质损伤力学和塑性流动理论,建立了基于能量耗散机制的塑性-损伤耦合模型。模型采用非关联塑性流动 法则描述混凝土不可恢复变形的演化。模拟刚度退化的损伤变量演化函数则通过断裂能和应力-非弹性应变空间中的累积 耗散能量建立。基于有限元程序 ABAQUS,推导了增量格式的材料雅可比矩阵,构建了塑性-损伤模型的仿真分析程序。应 用模型分析混凝土板平面内双轴受压试验、混凝土切口梁试验和钢筋混凝土梁受弯试验,计算获得的构件响应与试验结果 吻合良好,能够反映多轴应力状态对混凝土抗压强度的影响,也能准确模拟损伤导致的构件非线性反应。 关键词: 混凝土; 损伤力学; 塑性力学; 塑性-损伤模型; 仿真模拟 中图分类号: TU313 TU311. 41 文献标志码: A A plastic-damage model of concrete based on energy-loss mechanism LONG Yuchuan1,2 ,HOU Jianshan2 ,WANG Yushan3 ( 1. Key Laboratory of New Technology for Construction of Cities in Mountain Area ( Chongqing University) , Ministry of Education,Chongqing 400045,China; 2. School of Civil Engineering,Chongqing University,Chongqing 400045,China; 3. School of Hydraulic and Architectural Engineering,Shihezi University,Shihezi 832000,China) Abstract: A plastic-damage model was developed by using essential concepts of continuum damage mechanics and plastic flow theory. It employs a non-associated plastic flow rule to simulate the evolution of irrecoverable deformation. The evolutionary function of damage variable to model stiffness degradation was given in terms of the fracture energy and accumulated dissipated energy calculated according to the stress-inelastic strain relation. This model was implemented into ABAQUS,with the derivation of Jacobian matrix of material in rate form. This model was used to analyze biaxial compressive test of concrete slab,three-point-loading notched beam test and flexural test of reinforced concrete beam. Numerical results agree well with those obtained from tests. It is concluded that the plastic-damage model can represent the effects of multi-axial loading state on the compressive strength and simulate the nonlinear structural response due to damage. Keywords: concrete; damage mechanics; plastic mechanics; plastic-damage model; numerical simulation 基金项目: 国家自然科学基金项目( 51578088) ,新疆生产建设兵团博士基金项目( 2012BB013) 。 作者简介: 龙渝川( 1980— ) ,男,重庆人,工学博士,副教授。E-mail: longyc02@ cqu. edu. cn 收稿日期: 2016 年 7 月 147

0引言 1塑性损伤模型 塑性损伤模型是混凝土损伤非线性分析的基础 11模型建立 模型,综合了损伤力学与塑性流动理论,用以描迷加 基于标量损伤概念,可以建立总应力。与有效 我过程中混凝土的刚度退化与不可恢复变形 应力之间的关系,其中有效应力与应变E、塑性 m等基于各向同性损伤假设,提出 应变满足胡克定律。矩阵形式的应力应变关系为 了标量伤模型,模拉了湿凝士材料的度退化 =(1-d0=0 P) 式中:d为损伤因子 与标量损伤模型相结合,提出了塑性标量损 模型 构矩阵,、 性 通过构建基于断裂能概 念的损伤 函数和 向量 关联塑性 动法则,分别描述了混凝士的刚度退化 采用Lablinear等提出的多硬化变量屈服函 。基于标量损伤概念,W 数,其表达式为 Richar 等 采用能量释放率构建 损伤演化函数,建立了基于不可逆热力学框架的型 =。-3师+B门-ie 性标量损伤模型。此后,Scim引入非局部化损 其中 伤力学,通过构造非局部化的内能和耗散能函数,建 (3) 立损伤演化规律,提出了塑性-非局部化损伤模型。 由于混凝土损伤行为具有明显的各向异性特 (4) 、L0等四基于二阶损伤张量和边界面 a0-( 概念,建立了基于能量释放率概念的各向异性损伤 n=-3:1 (5) 模型,该模型较好地模拟了单轴加载下混凝土的非 线性行为。Voviadiis等和AR等用一阶 (6) 损伤张量和应力张量的谱分解方法,构建了基于能 量释放率的损伤张量化函数,建立了翔性各向异 式中:a~B为无量纲量:为最大主应力:可(c) 性损伤榄型,并拟了多轴应力状态下的混土精 行(s)分别为受压、受拉有效应力,是塑性应变s 伤行为 近年类,W和八g等基于热力气 的函激:、分别为混凝土双轴抗压和单轴抗压 架,在张量损伤模型中引入满足热力学基木定律 强度:万,。分别为有效应力张量的第一、第二不 了传统损伤模型难 量,由有教应力张量示和偏应力形量令确定,其中 s=可+:I为二阶单位张量。()为Me Cauley 结合,建立 混凝士随机损伤 学模型 数(x)=(x+xD。 上述研究表 基于能量耗散 定义损伤演化规 则,可有效描述混凝 刚度退化规 然而,基于 塑性应变向量由流动法则确定,满足: 性耗能、能量释放率定义的损伤演化规则,无法明确 (7) 提出以应力非弹性应变空间的累积耗 散能量为自变量,构建损伤演化函数,同时为反映非 由:为期性 线性卸载/线性重加载应力路径模拟滞回行为,建立 心率参数 曲型势函数 顶点处的曲 了考虑滞回耗能影响的损伤模型。然而,该模型未 为湿 心抗拉强度 混凝 膨胀角,由高 采用塑性流动理论,难以准确模拟复杂应力状态下 压应力约束条件下的可关系测量获得 的不可恢复变形。 加卸载条件为认≥0,F≤0,dM·F=0。定 本文在塑性标量损伤模型中引入基于能量耗散 义标量损伤因子d为: 的损伤演化规侧,然后采用屈服函数和塑性流动法 d=1-(1-s,d)(1-,d) (8) 则,描述加载过程中混凝土的刚度退化与不可恢复 3.=1-g.r (9) 变形,以期为分析混凝土结构损伤行为提供参考 .=1-a.1-) (10) 148 1994-2017China Academic Joural Electronic Publishing House.All rights reserved. http://www.cnki.ne
0 引言 塑性-损伤模型是混凝土损伤非线性分析的基础 模型,综合了损伤力学与塑性流动理论,用以描述加 载过 程 中 混 凝 土 的 刚 度 退 化 与 不 可 恢 复 变 形。 Mazars [1]、Cervera 等[2]基于各向同性损伤假设,提出 了标量损伤模型,模拟了混凝土材料的刚度退化。 Lublinear 等[3]、Lee 等[4]、Faria 等[5]将塑性流动法则 与标量损伤模型相结合,提出了塑性-标量损伤模型, 通过构建基于断裂能概念的损伤演化函数和引入非 关联塑性流动法则,分别描述了混凝土的刚度退化 与不 可 恢 复 累 积 变 形。基 于 标 量 损 伤 概 念,Wu 等[6]、Zhang 等[7]、Richard 等[8]采用能量释放率构建 损伤演化函数,建立了基于不可逆热力学框架的塑 性-标量损伤模型。此后,Sciarra [9] 引入非局部化损 伤力学,通过构造非局部化的内能和耗散能函数,建 立损伤演化规律,提出了塑性-非局部化损伤模型。 由于混凝土损伤行为具有明显的各向异性特 性,Alliche [10]、L 等[11]基于二阶损伤张量和边界面 概念,建立了基于能量释放率概念的各向异性损伤 模型,该模型较好地模拟了单轴加载下混凝土的非 线性行为。Voyiadjis 等[12]和 Al-Rub 等[13]采用二阶 损伤张量和应力张量的谱分解方法,构建了基于能 量释放率的损伤张量演化函数,建立了塑性-各向异 性损伤模型,并模拟了多轴应力状态下的混凝土损 伤行为。近年来,Wu 等[14]和 Ngo 等[15]基于热力学 框架,在张量损伤模型中引入满足热力学基本定律 的映射算子,解决了传统损伤模型难以满足能量守 恒的问题。此外,还有研究者将损伤模型与随机力 学相结合,建立了混凝土随机损伤力学模型[16]。 上述研究表明,基于能量耗散定义损伤演化规 则,可有效描述混凝土刚度退化规律。然而,基于塑 性耗能、能量释放率定义的损伤演化规则,无法明确 反映加卸载过程中损伤演化与总耗散能量的关系。 龙渝川等[17]提出以应力-非弹性应变空间的累积耗 散能量为自变量,构建损伤演化函数,同时为反映非 线性卸载/线性重加载应力路径模拟滞回行为,建立 了考虑滞回耗能影响的损伤模型。然而,该模型未 采用塑性流动理论,难以准确模拟复杂应力状态下 的不可恢复变形。 本文在塑性-标量损伤模型中引入基于能量耗散 的损伤演化规则,然后采用屈服函数和塑性流动法 则,描述加载过程中混凝土的刚度退化与不可恢复 变形,以期为分析混凝土结构损伤行为提供参考。 1 塑性-损伤模型 1. 1 模型建立 基于标量损伤概念,可以建立总应力 σ 与有效 应力 σ珔之间的关系,其中有效应力 σ珔与应变 ε 、塑性 应变 ε p 满足胡克定律。矩阵形式的应力-应变关系为: σ = ( 1 - d) σ珔= ( 1 - d) E( ε - ε p ) ( 1) 式中: d 为损伤因子,由损伤演化规则确定; E 为线 弹性本构矩阵,ε 、ε p 分别为总应变向量和塑性应变 向量。 采用 Lublinear 等[3] 提出的 多 硬 化 变 量 屈 服 函 数,其表达式为: F = 1 1 - α [q珋- 3αp珋+ β〈σ珚max 〉]- σ珚' c ( εp c ) ( 2) 其中, α = fb - fc 2fb - fc ( 3) β = σ珚' c ( εp c ) σ珚' t ( εp t ) ( 1 - α) - ( 1 + α) ( 4) p珋= - 1 3 σ珔∶ I ( 5) q珋= 3 2 槡 s ∶ s ( 6) 式中: α、β 为无量纲量; σ珚max 为最大主应力; σ珚' c ( εp c ) 、 σ珚' t ( εp t ) 分别为受压、受拉有效应力,是塑性应变 εp c 、 εp t 的函数; fb、fc 分别为混凝土双轴抗压和单轴抗压 强度; p珋、q珋分别为有效应力张量的第一、第二不变 量,由有效应力张量 σ珔和偏应力张量 s 确定,其中 s = σ珔+ p珋I; I 为二阶单位张量。〈·〉为 Mc Cauley 函 数,〈x〉= 1 2 ( x + x ) 。 塑性应变向量 ε p 由流动法则确定,满足: dε p = dλ·Gq 珔σ ( 7) Gq = ( ζft tanψ) 2 槡 + q珋 2 - p珋tanψ 式中: λ 为塑性一致性参数; Gq 为塑性势函数; ζ 为 离心率参数,表征双曲型势函数 Gq 在顶点处的曲率; ft 为混凝土轴心抗拉强度; ψ 为混凝土膨胀角,由高 压应力约束条件下的 p珋-q珋关系测量获得。 加卸载条件为 dλ ≥ 0 ,F ≤ 0 ,dλ·F = 0 。定 义标量损伤因子 d 为: d = 1 - ( 1 - stdc ) ( 1 - scdt ) ( 8) st = 1 - ωtr ( 9) sc = 1 - ωc ( 1 - r) ( 10) 148

其中:d,d分别为受拉或受压损伤变量:5为由受压 状态进入受拉状态时的刚度恢复权函数:仙,为与$ 4=(,所= 相应的刚度恢复系数,取值区间为0,1]:s,为由受 拉状态讲入受压状态时的刚度恢复权函新:切为与 4(月后=g (16) 相应的刚度恢复系数,取值范围也为0,1门]。引入 式中:GG分别为受拉受压断裂能:g分别为 仙,和仙。的目的是模拟拉压应力状态转换时存在的 受拉,受压断裂能密度:h为表征裂缝带宽度的单元 刚度恢复现象,即单侧效应:=,)/∑1n 尺寸:0,0,为损伤指数,由试验数据拟合确定, 为多轴应力状态下的状态函数,由各应力主轴的应 2 塑性损伤模型的有限元实现 力强度比,=立确定,其中,为第:轴的主应力, 为相应的有效应力强度,当,>0时,人=,当 基于有限元程序ABAOUS的二次开发功能,编 制塑性损伤模型的用户子程序,实现该模型的分析 0:≤0时,f=-元 1.2拉,压损伤变量 功能。采用线性化方法,构建增量形式的结构平衡 方程,解决塑性损伤模型导致的材料非线性问题。 模型中,拉、压损伤变量由累积耗散能与混凝土 矩阵形式的增量平衡方程为 断裂能的比值定义。将应变张量分解为弹性应变 和非弹性应变£之和,即 KAU =AP (17) 式中,K为增量形式的结构整体刚度矩阵,△U、△P 分别为节点的位移增量和等效荷增量 满足 a =E' (12 整体刚度矩阵K由积分点处的材料雅可比矩阵 由于应力与弹性应变产生的应变能可逆,不有 确定,△P与积分点处的总应力相关 在能量耗散,因此,累积耗散能由应力。与非弹性应 塑性损伤模型的有限元分析,店 变“确定。如图1所示,拉、压累积样散能量分别根 应力和雅可比矩 据拉应力主轴和压应力主轴上的应力非弹性应变关 图2为塑性损伤模型计算流程示意,整个计 系计算,满足 过程由求解 效应力与 计算 损伤因 =da,de o,de"o (e-e) 胸建推可比矩 部分组成,图中 云分别为 有效应力向量的最 大主应力和最小主应 力根据 (13 2)给定的屈服函数和式(7)给出的流动法则,构廷 B:=do.de =a.de"-To,(ei-p) 牛顿迭代求解有效应力和塑性应变:根据式(13 (16)构建牛顿迭代求解损伤因子。按图2所示流君 获得有效应力和损伤因子d后,可由式(1)确定积分 武中: 、分别为拉、压累积耗散能的积分区域 点的总应力0,进而获得等效节点荷载增量△P 即图1中阴影所示区域:4、、分别为A点的 雅可比矩阵是组成结构刚度矩阵的关健要素 受拉应力,非弹性应变和塑性应变:。片、则分 直接影响材料非线性问题的求解效率。雅可比矩阵 别为B点的受压应力、非弹性应变和塑性应变。 可由式(1)求导获得,即 =(1-后-=1-dE-) 根据屈服函数、塑性流动法则和加卸栽条件,塑 性应变”与总应变后应满足: E”=e (19) E (20) 《a)受拉积耗散 (b)受压制耗敢能 H=E-1)g 式中:〔=F/5、f=F/a"分别为屈服函数对有 图1 累积耗散能计算示意 Fig.I Coe 效应力和塑性应变的导数向量:9为塑性势函数对 isipated ene 有效应力的导数向量,g=G,/5。f、f、g均为n 获得积耗散能量后,混凝土拉、压损伤变量计 ×1的向量(二维n=3,三维m=6)。 算式分别为 过式(8)以及式(13)-(16),可以得到 149 1994-20 7China Academic Joural Electronic Publishing House.All rights reserved.htp://www.enki.net
其中: dt、dc 分别为受拉或受压损伤变量; st 为由受压 状态进入受拉状态时的刚度恢复权函数; ωt 为与 st 相应的刚度恢复系数,取值区间为[0,1]; sc 为由受 拉状态进入受压状态时的刚度恢复权函数; ωc 为与 sc 相应的刚度恢复系数,取值范围也为[0,1]。引入 ωt 和 ωc 的目的是模拟拉-压应力状态转换时存在的 刚度恢复现象,即单侧效应; r = ∑ 3 i = 1 〈ηi〉 ∑ 3 i = 1 ηi 为多轴应力状态下的状态函数,由各应力主轴的应 力强度比 ηi = σ珟i fi 确定,其中 σ珟i 为第 i 轴的主应力,fi 为相应的有效应力强度,当 σ珟i > 0 时,fi = σ珟' t ,当 σ珟i ≤0 时,fi = - σ珚' c 。 1. 2 拉、压损伤变量 模型中,拉、压损伤变量由累积耗散能与混凝土 断裂能的比值定义。将应变张量 ε 分解为弹性应变 ε e 和非弹性应变 ε in 之和,即 ε = ε e + ε in ( 11) 满足 σ = Eε e ( 12) 由于应力与弹性应变产生的应变能可逆,不存 在能量耗散,因此,累积耗散能由应力 σ 与非弹性应 变 ε in 确定。如图 1 所示,拉、压累积耗散能量分别根 据拉应力主轴和压应力主轴上的应力-非弹性应变关 系计算,满足: Ed t = ∫Ω+ dσtdεin t = ∫ εin A 0 σtdεin t - 1 2 σA ( εin A - εp A ) ( 13) Ed c = ∫Ω- dσcdεin c = ∫ εin B 0 σcdεin c - 1 2 σB ( εin B - εp B ) ( 14) 式中: Ω+ 、Ω- 分别为拉、压累积耗散能的积分区域, 即图 1 中阴影所示区域; σA 、εin A 、εp A 分别为 A 点的 受拉应力、非弹性应变和塑性应变; σB 、εin B 、εp B 则分 别为 B 点的受压应力、非弹性应变和塑性应变。 图 1 累积耗散能计算示意 Fig. 1 Computation of accumulated dissipated energy 获得累积耗散能量后,混凝土拉、压损伤变量计 算式分别为: dt = Ed t g ( )t f θt ,gt f = Gt f h ( 15) dc = Ed c g ( ) c f θc ,gc f = Gc f h ( 16) 式中: Gt f、Gc f 分别为受拉、受压断裂能; gt f、gc f 分别为 受拉、受压断裂能密度; h 为表征裂缝带宽度的单元 尺寸; θt、θc 为损伤指数,由试验数据拟合确定。 2 塑性-损伤模型的有限元实现 基于有限元程序 ABAQUS 的二次开发功能,编 制塑性-损伤模型的用户子程序,实现该模型的分析 功能。采用线性化方法,构建增量形式的结构平衡 方程,解决塑性-损伤模型导致的材料非线性问题。 矩阵形式的增量平衡方程为 KΔu = ΔP ( 17) 式中,K 为增量形式的结构整体刚度矩阵,Δu 、ΔP 分别为节点的位移增量和等效荷载增量。 整体刚度矩阵 K 由积分点处的材料雅可比矩阵 确定,ΔP 与积分点处的总应力相关。因此,为实现 塑性-损伤模型的有限元分析,应获得任意时刻的总 应力和雅可比矩阵。 图 2 为塑性-损伤模型计算流程示意,整个计算 过程由求解有效应力与塑性应变、计算损伤因子和 构建雅可比矩阵三部分组成,图中 σ珚max 、σ珚min 分别为 有效应力向量的最大主应力和最小主应力。根据式 ( 2) 给定的屈服函数和式( 7) 给出的流动法则,构建 牛顿迭代求解有效应力和塑性应变; 根据式( 13) ~ ( 16) 构建牛顿迭代求解损伤因子。按图 2 所示流程 获得有效应力和损伤因子 d 后,可由式( 1) 确定积分 点的总应力 σ ,进而获得等效节点荷载增量 ΔP 。 雅可比矩阵是组成结构刚度矩阵的关键要素, 直接影响材料非线性问题的求解效率。雅可比矩阵 可由式( 1) 求导获得,即 σ = ( 1 - d) σ珔 · - d · σ珔= ( 1 - d) E( ε - ε p ) - d · σ珔 ( 18) 根据屈服函数、塑性流动法则和加卸载条件,塑 性应变 ε p 与总应变 ε 应满足: ε p = H ε ( 19) H = f T s E ( f T s E - f T e ) g ( 20) 式中: fs = F/珔σ、fe = F/ε p 分别为屈服函数对有 效应力和塑性应变的导数向量; g 为塑性势函数对 有效应力的导数向量,g = Gq /珔σ 。fs、fe、g 均为 n × 1 的向量( 二维 n = 3,三维 n = 6) 。 通过式( 8) 以及式( 13) ~ ( 16) ,可以得到: 149
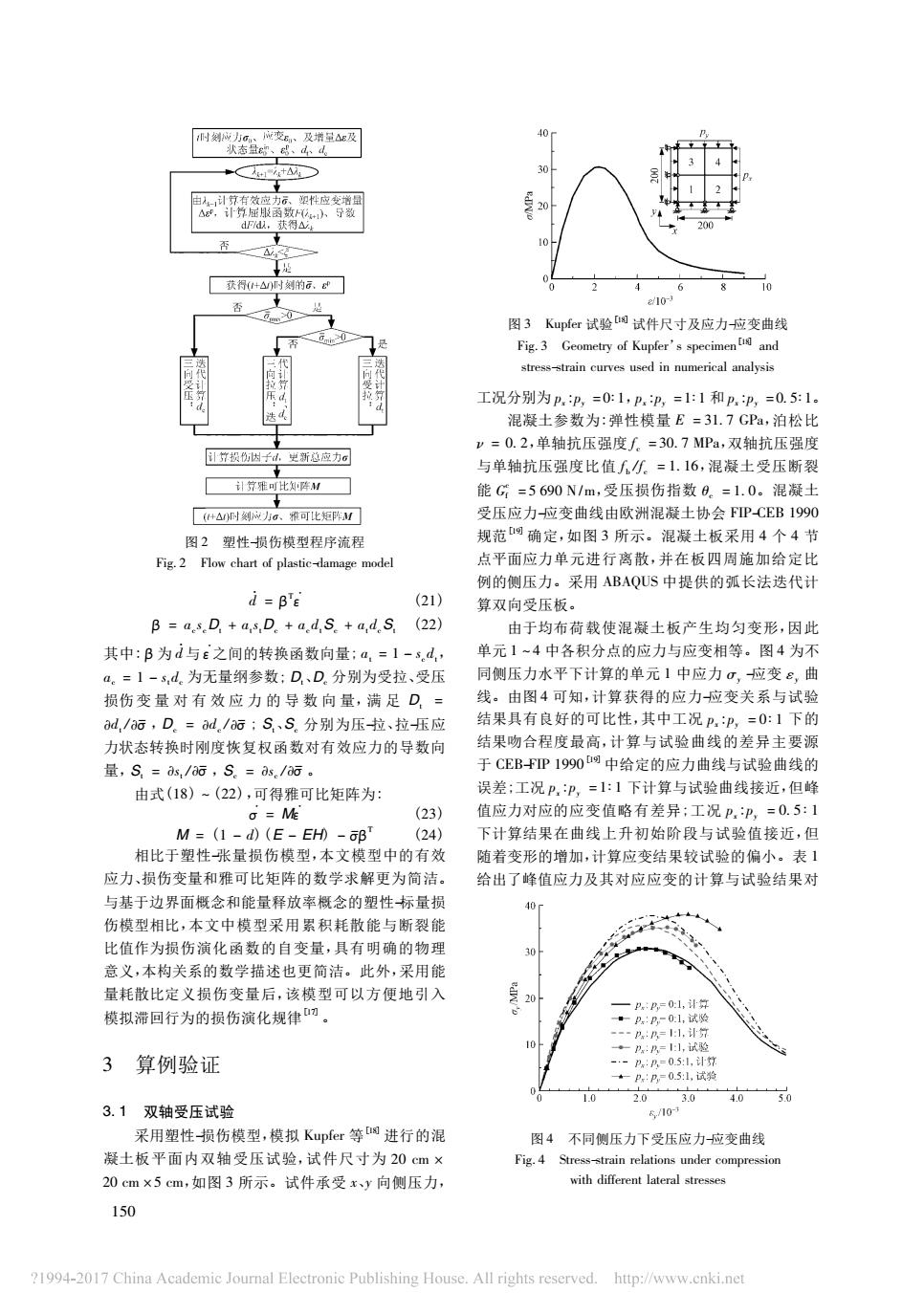
时:及特及 7 20 否 0 8 图3Kpr试验试件尺寸及应力应变曲线 Fig.3 Geometry of Kupfer's specimen and stress-strain curves used in numerical analysis 混凝 ,泊松 ”=0.2,单轴抗压强度.=30.7 MPa,双轴抗压强 计算损出 所总应力 与单轴抗压强度比值人=1.16,混凝土受压断裂 能G=5690N/m,受压损伤指数8.=1.0。混凝士 厂d阿 受压应力应变曲线由欧洲混凝土协会FP-CEB1990 、 塑性损伤模型程序流 规范阿确定,如图3所示。混凝土板采用4个4出 Fig.2 点平面应力单元进行离散,并在板四周能加给定比 例的侧压力。采用ABAOUS中提供的弧长法迭代计 d=BE (21 算双向受压板 B a,s.D.a,s,D.a.d,S.a,d.S.(22) 由于均布荷找使混凝土板产生均匀变形,因 其中:B为d与E之间的转换函数向量 单元1-4中各积分点的应力与应变相等,图4为不 a,=1-5d为无量纲参数:D、D.分别为受拉 受 司侧压力水平下计算的单元中应 损伤变量对有效应力的导数向量,满足D= 变关系 d/近,D=d/G:S,S。分别为压拉.拉压应 力状态转换时刚度恢复权丽数对有效应力的导数向 试鸭 的差」 .S=as/a s =as /a 由式(18)-(22),可得雅可比矩阵为: 况,p,=:1下计算 线接近,但 =M (23) 值应力对应的应变值略有差异:工况P,p,=0. M=(1-d)(E-Eh-邱 (24 下计算结果在曲线上升初始阶段与试验值接近,但 相比于塑性张量损伤模型,本文模型中的有效 随着变形的增加,计算应变结果较试验的偏小。表 应力、损伤变量和雅可比矩阵的数学求解更为简洁。 给出了峰值应力及其对应应变的计算与试验结果对 与基于边界面概念和能量释放率概念的塑性标量损 伤模型相比,本文中模型采用累积耗散能与断裂能 比值作为损伤演化函数的自变量,具有明确的物理 意义,本构关系的数学描述也更简洁。此外,采用能 量耗散比定义损伤变量后,该模型可以方便地引入 揽拟滞回行为的揭伤演化规律 3算例验证 3.1双轴受压试验 s/0 采用塑性损伤模型,模拟Kupfer等圆进行的混 图4不同侧压力下受压应力应变曲线 凝土板平面内双轴受压试验,试件尺寸为20cm× Fig.4 Su 20cm×5cm,如图3所示。试件承受xy向侧压力, with different lateral stresses 150 1994-2017 China Academic Joural Electronic Publishing House.All rights reserved.hup://www.enki.ne
图 2 塑性-损伤模型程序流程 Fig. 2 Flow chart of plastic-damage model d · = β T ε ( 21) β = ac scDt + atstDc + acdtSc + atdcSt ( 22) 其中: β 为 d · 与 ε 之间的转换函数向量; at = 1 - scdt, ac = 1 - stdc 为无量纲参数; Dt、Dc 分别为受拉、受压 损伤 变 量 对 有 效 应 力 的 导 数 向 量,满 足 Dt = dt /珔σ ,Dc = dc /珔σ ; St、Sc 分别为压-拉、拉-压应 力状态转换时刚度恢复权函数对有效应力的导数向 量,St = st /珔σ ,Sc = sc /珔σ 。 由式( 18) ~ ( 22) ,可得雅可比矩阵为: σ = M ε ( 23) M = ( 1 - d) ( E - EH) - σβ珔T ( 24) 相比于塑性-张量损伤模型,本文模型中的有效 应力、损伤变量和雅可比矩阵的数学求解更为简洁。 与基于边界面概念和能量释放率概念的塑性-标量损 伤模型相比,本文中模型采用累积耗散能与断裂能 比值作为损伤演化函数的自变量,具有明确的物理 意义,本构关系的数学描述也更简洁。此外,采用能 量耗散比定义损伤变量后,该模型可以方便地引入 模拟滞回行为的损伤演化规律[17]。 3 算例验证 3. 1 双轴受压试验 采用塑性-损伤模型,模拟 Kupfer 等[18]进行的混 凝土板平面内双轴受压试验,试件尺寸为 20 cm × 20 cm × 5 cm,如图 3 所示。试件承受 x、y 向侧压力, 图 3 Kupfer 试验[18]试件尺寸及应力-应变曲线 Fig. 3 Geometry of Kupfer’s specimen [18] and stress-strain curves used in numerical analysis 工况分别为 px : py = 0∶ 1,px : py = 1∶ 1 和 px : py = 0. 5∶ 1。 混凝土参数为: 弹性模量 E = 31. 7 GPa,泊松比 ν = 0. 2,单轴抗压强度 fc = 30. 7 MPa,双轴抗压强度 与单轴抗压强度比值 fb /fc = 1. 16,混凝土受压断裂 能 Gc f = 5 690 N/m,受压损伤指数 θc = 1. 0。混凝土 受压应力-应变曲线由欧洲混凝土协会 FIP-CEB 1990 规范[19]确定,如图 3 所示。混凝土板采用 4 个 4 节 点平面应力单元进行离散,并在板四周施加给定比 例的侧压力。采用 ABAQUS 中提供的弧长法迭代计 算双向受压板。 图 4 不同侧压力下受压应力-应变曲线 Fig. 4 Stress-strain relations under compression with different lateral stresses 由于均布荷载使混凝土板产生均匀变形,因此 单元 1 ~ 4 中各积分点的应力与应变相等。图 4 为不 同侧压力水平下计算的单元 1 中应力 σy -应变 εy 曲 线。由图 4 可知,计算获得的应力-应变关系与试验 结果具有良好的可比性,其中工况 px : py = 0∶ 1 下的 结果吻合程度最高,计算与试验曲线的差异主要源 于 CEB-FIP 1990 [19]中给定的应力曲线与试验曲线的 误差; 工况 px : py = 1∶ 1 下计算与试验曲线接近,但峰 值应力对应的应变值略有差异; 工况 px : py = 0. 5 ∶ 1 下计算结果在曲线上升初始阶段与试验值接近,但 随着变形的增加,计算应变结果较试验的偏小。表 1 给出了峰值应力及其对应应变的计算与试验结果对 150
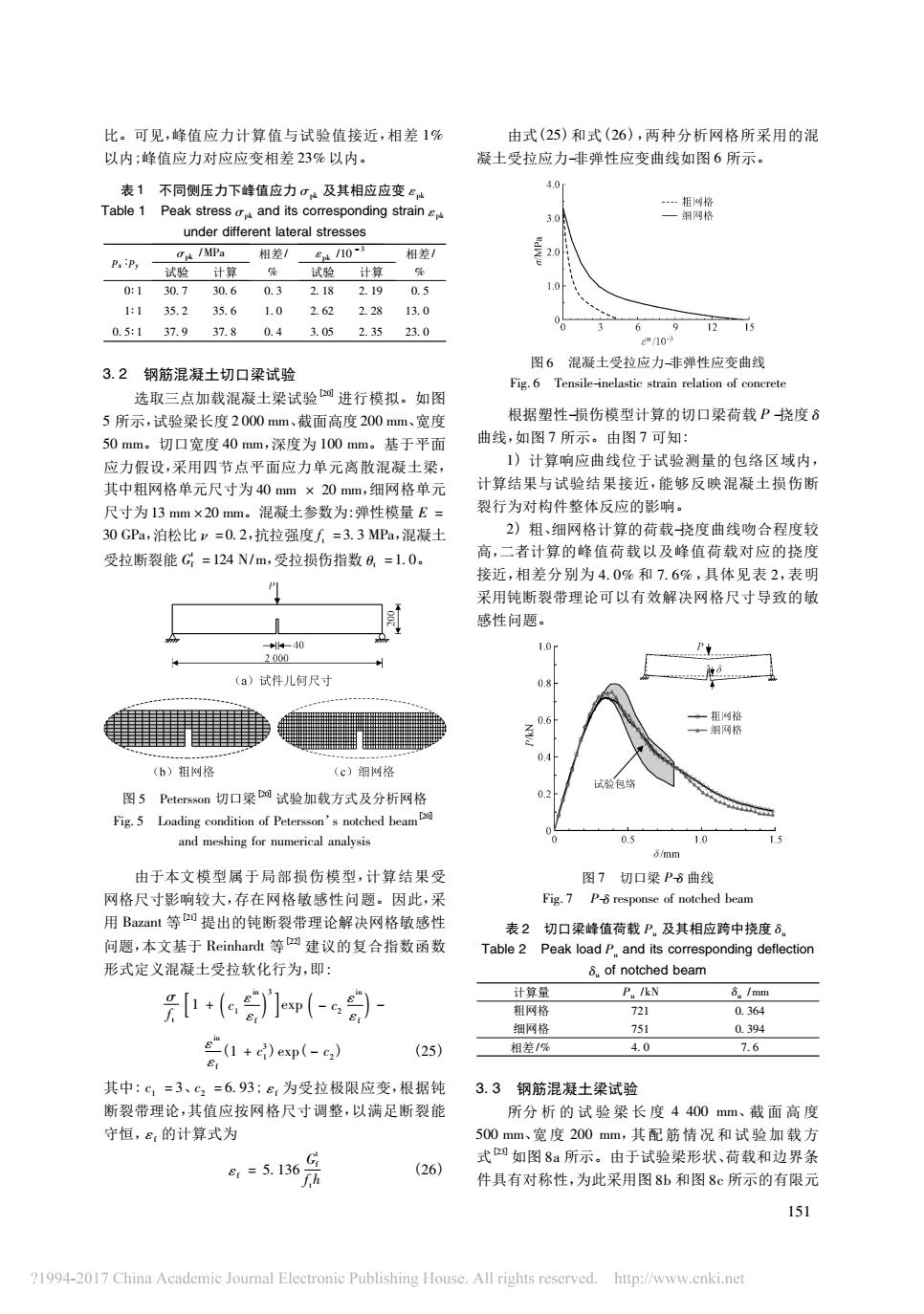
比。可见,峰值应力计算值与试验值接近,相差1% 由式(25)和式(26),两种分析网格所采用的混 以内:峰值应力对应应变相差23%以内。 凝土受拉应力-非弹性应变曲线如图6所示。 1 不同侧压力下蜂值应力:及其相应应变+ 40 Table 1 Peak stress and onding strain s 二 lateral stresses 相 20 计 计算 0:130.7 30.60.3 2182190.3 10 11 35. 35.6 1.0 26@ 22810 0.5:137.g 37.8 0.4 3.05 2.35 75 23.0 3.2钢筋混凝士切口梁试验 土梁试验进行模拟。如 根据塑性损伤模型计算的切口梁荷载P挠度6 曲线,如图7所示,由图7知 50 mm 切口宽度40m ,为10mm 基于平 应力假设,采用四节点平面应力单元离散混凝土梁 1)计算响应曲线位于试验测量的包络区域内 其中粗网格单元尺寸为40mm×20mm,细网格单元 计算结果与试验结果接近,能够反映混凝土损伤博 尺寸为13mm×20mm. 混凝土参数为:弹性模量E 裂行为对物件整体反应的影响 30GPa,泊松比"=0.2,抗拉强度f=3.3MPa,混凝士 2)粗、细故计算的益数挠度曲线吻合程度 受拉断裂能G=124N/m,受拉损伤指数6,=1.0. 高,二者计算的峰值荷载以及蜂值荷载对应的挠度 接近,相差分别为4.0%和7.6%,具体见表2,表明 采用纯断裂带理论可以有效解决网格尺寸导致的敏 感性问题, 20 (a)试件儿何尺寸 b)相倒格 《c)细格 图5 Pm切口梁试验加载方式及分析网格 0.5 10 由于本文候型属于局部损伤模型,计算结果受 图7 网格尺寸影 网格敏感性问题 因此, Fig.7 Pp beam 用Bazant 表2切口梁培值荷载P及其相应跨中挠度8 问题,本文基于Reinhardt等建议的复合指数函数 Table 2 Peak load p and its corresponding deflection 形式定义混凝土受拉款化行为,即: 8.of notched beam +6门卿(-6) 计算量 P./N 8./mm 751 03 1+6》op(-e (25】 相老第 4.0 7.6 603 3.3 钢筋混凝土梁试验 所分析的试验梁长度4400mm、截面高度 守恒,,的计算式为 500mm,宽度200mm,其配筋情况和试验加载 =51B6月 (26 如图8a所示。由于试验梁形状,荷载和边界务 件具有对称性,为此采用图8h和图8e所示的有限元 151 4-017China Electron Publishing House.All rights reserved.htp://ww
比。可见,峰值应力计算值与试验值接近,相差 1% 以内; 峰值应力对应应变相差 23% 以内。 表 1 不同侧压力下峰值应力 σpk 及其相应应变 εpk Table 1 Peak stress σpk and its corresponding strain εpk under different lateral stresses px : py σpk /MPa 试验 计算 相差/ % εpk /10 - 3 试验 计算 相差/ % 0∶ 1 30. 7 30. 6 0. 3 2. 18 2. 19 0. 5 1∶ 1 35. 2 35. 6 1. 0 2. 62 2. 28 13. 0 0. 5∶ 1 37. 9 37. 8 0. 4 3. 05 2. 35 23. 0 3. 2 钢筋混凝土切口梁试验 选取三点加载混凝土梁试验[20]进行模拟。如图 5 所示,试验梁长度 2 000 mm、截面高度 200 mm、宽度 50 mm。切口宽度 40 mm,深度为 100 mm。基于平面 应力假设,采用四节点平面应力单元离散混凝土梁, 其中粗网格单元尺寸为 40 mm × 20 mm,细网格单元 尺寸为 13 mm × 20 mm。混凝土参数为: 弹性模量 E = 30 GPa,泊松比 ν = 0. 2,抗拉强度 ft = 3. 3 MPa,混凝土 受拉断裂能 Gt f = 124 N/m,受拉损伤指数 θt = 1. 0。 图 5 Petersson 切口梁[20]试验加载方式及分析网格 Fig. 5 Loading condition of Petersson’s notched beam[20] and meshing for numerical analysis 由于本文模型属于局部损伤模型,计算结果受 网格尺寸影响较大,存在网格敏感性问题。因此,采 用 Bazant 等[21]提出的钝断裂带理论解决网格敏感性 问题,本文基于 Reinhardt 等[22]建议的复合指数函数 形式定义混凝土受拉软化行为,即: σ ft 1 + c1 εin ε ( )f [ ] 3 exp - c2 εin ε ( )f - εin εf ( 1 + c 3 1 ) exp( - c2 ) ( 25) 其中: c1 = 3、c2 = 6. 93; εf 为受拉极限应变,根据钝 断裂带理论,其值应按网格尺寸调整,以满足断裂能 守恒,εf 的计算式为 εf = 5. 136 Gt f fth ( 26) 由式( 25) 和式( 26) ,两种分析网格所采用的混 凝土受拉应力-非弹性应变曲线如图 6 所示。 图 6 混凝土受拉应力-非弹性应变曲线 Fig. 6 Tensile-inelastic strain relation of concrete 根据塑性-损伤模型计算的切口梁荷载 P -挠度 δ 曲线,如图 7 所示。由图 7 可知: 1) 计算响应曲线位于试验测量的包络区域内, 计算结果与试验结果接近,能够反映混凝土损伤断 裂行为对构件整体反应的影响。 2) 粗、细网格计算的荷载-挠度曲线吻合程度较 高,二者计算的峰值荷载以及峰值荷载对应的挠度 接近,相差分别为 4. 0% 和 7. 6% ,具体见表 2,表明 采用钝断裂带理论可以有效解决网格尺寸导致的敏 感性问题。 图 7 切口梁 P-δ 曲线 Fig. 7 P-δ response of notched beam 表 2 切口梁峰值荷载 Pu 及其相应跨中挠度 δu Table 2 Peak load Pu and its corresponding deflection δu of notched beam 计算量 Pu /kN δu /mm 粗网格 721 0. 364 细网格 751 0. 394 相差/% 4. 0 7. 6 3. 3 钢筋混凝土梁试验 所分 析 的 试 验 梁 长 度 4 400 mm、截 面 高 度 500 mm、宽 度 200 mm,其 配 筋 情 况 和 试 验 加 载 方 式[23]如图 8a 所示。由于试验梁形状、荷载和边界条 件具有对称性,为此采用图 8b 和图 8c 所示的有限元 151

小8@100 出 2025/ 160 0102 304.050 020406080i a)试件几何尺时 (a)把凝+漫拉 (b)深凝十受出 B00 L 3 (b)混凝上网格及成方式 20406080i00 o20406080i0 食 心》线白幽铭 图9混凝土及锅筋应力应变曲线 and stirmps 图8钢筋混凝士梁阳试验加载方式及分析网格 Fig.8 Loading condition of RC heam and meshing for numerical analvsis 网格、加载方式和边界条件进行模拟。其中,混凝士 梁采用四节点平面应力单元进行离散,纵向钢筋和 箱筋采用双节点杆单元进行离散。钢筋单元嵌入混 二计 凝土单元中,并与后者保持变形协调。 材料参数取值如下:混服土弹性模量E=37GP 30 泊松比p=0.2,抗拉强度=2.14MPa,抗压强度 31.8MPa,受拉、受压应力应李曲线由GB50010 2010混凝士结物设计却范》中公式确定,相应的受拉 和受压断裂能分别为C=2440N/m,G=26800N/m 1)计算得到的变拒地度曲线与球验结果铲诉 受拉及受压损伤指数分别为8,=1.0和日 =10- 反映了加载过程中弹性阶段、开裂阶段和破坏阶段 200GPa,纵向钢筋屈服强度和抗 到密湿基斗没的度变化 470MPa和 2)计算获得的开裂弯矩、屈服弯矩、极限弯矩与 拉强度分别) 试验结果吻合较好,相差不超过10%,能够模拟混凝 507 MPa 图9给 了混海土 467 MPa 纵向钢筋和箍筋的 土损伤对钢筋混凝土构件反应的影响。 力应变曲线,其中,,分别表示纵向钢筋的应力 与应变,。·8。分别表示箍筋的应力与应变。 4 结论 图10给出了计算和试验获得的跨中弯矩M 度8曲线,表3将模型计算的开裂弯矩M、屈服弯炬 )塑性损伤模型能够模拟双轴受压混凝土的 M,和极限弯矩M。与试验值进行了对比。可以看出: 非线性行为,计算的峰值应力与试验结果相差小 1%,可以反映多轴应力对混凝土抗压强度的影响 表3开裂弯矩M。屈服弯矩M,和极限弯矩M,对比 )由模型计算得到的混凝土切口梁荷载挠度 Table 3 Compan ons tor cracking moment yielding mom ent and u 曲线与试验曲线接近,能够模拟混凝土损伤断裂 te moment A 构件整体反应的影响,并可采用钝断裂带理论解法 网格尺寸导致的敏感性问题。 计分 30110 3)计算获得的钢筋混凝土梁弯矩挠度曲线与 相修 81 48 16 试验曲线吻合较好,反映了混凝土损伤对构件刚度 的影响,能够用于钢筋混凝土结构的非线性分析。 152 1994-2017 China Academic Joumal Electronic Publishing House.All rights reserved.hup://www.enki.net
图 8 钢筋混凝土梁[23]试验加载方式及分析网格 Fig. 8 Loading condition of RC beam[23] and meshing for numerical analysis 网格、加载方式和边界条件进行模拟。其中,混凝土 梁采用四节点平面应力单元进行离散,纵向钢筋和 箍筋采用双节点杆单元进行离散。钢筋单元嵌入混 凝土单元中,并与后者保持变形协调。 材料参数取值如下: 混凝土弹性模量 E = 37 GPa, 泊松比 ν = 0. 2,抗拉强度 ft = 2. 14 MPa,抗压强度 fc = 31. 8 MPa,受 拉、受 压 应 力-应 变 曲 线 由 GB 50010— 2010《混凝土结构设计规范》中公式确定,相应的受拉 和受压断裂能分别为 Gt f = 2 440 N/m,Gc f = 26 800 N/m, 受拉及受压损伤指数分别为 θt = 1. 0 和 θc = 1. 0; 钢 筋弹性模量为 Es = 200 GPa,纵向钢筋屈服强度和抗 拉强度分别为 fy = 470 MPa 和 fu = 660 MPa,箍筋屈 服强度 和 抗 拉 强 度 分 别 为 fsy = 467 MPa 和 fsu = 507 MPa。图 9 给出了混凝土、纵向钢筋和箍筋的应 力-应变曲线,其中,σs 、εs 分别表示纵向钢筋的应力 与应变,σst 、εst 分别表示箍筋的应力与应变。 图 10 给出了计算和试验获得的跨中弯矩 M -挠 度 δ 曲线,表 3 将模型计算的开裂弯矩 Mcr、屈服弯矩 My 和极限弯矩 Mu 与试验值进行了对比。可以看出: 表 3 开裂弯矩 Mcr 、屈服弯矩 My 和极限弯矩 Mu 对比 Table 3 Comparisons for cracking moment Mcr , yielding moment My and ultimate moment Mu 方法 Mcr /( kN·m) My /( kN·m) Mu /( kN·m) 试验 42. 57 193. 76 237. 92 计算 46. 00 203. 10 234. 00 相差/% 8. 1 4. 8 1. 6 图 9 混凝土及钢筋应力-应变曲线 Fig. 9 Stress-strain curves of concrete,reinforcement and stirrups 图 10 钢筋混凝土梁跨中弯矩 M -挠度 δ 曲线 Fig. 10 M-δ curves of reinforced concrete beam 1) 计算得到的弯矩-挠度曲线与试验结果接近, 反映了加载过程中弹性阶段、开裂阶段和破坏阶段 钢筋混凝土梁的刚度变化; 2) 计算获得的开裂弯矩、屈服弯矩、极限弯矩与 试验结果吻合较好,相差不超过 10% ,能够模拟混凝 土损伤对钢筋混凝土构件反应的影响。 4 结论 1) 塑性-损伤模型能够模拟双轴受压混凝土的 非线性行为,计算的峰值应力与试验结果相差小于 1% ,可以反映多轴应力对混凝土抗压强度的影响。 2) 由模型计算得到的混凝土切口梁荷载-挠度 曲线与试验曲线接近,能够模拟混凝土损伤断裂对 构件整体反应的影响,并可采用钝断裂带理论解决 网格尺寸导致的敏感性问题。 3) 计算获得的钢筋混凝土梁弯矩-挠度曲线与 试验曲线吻合较好,反映了混凝土损伤对构件刚度 的影响,能够用于钢筋混凝土结构的非线性分析。 152

参考文献 simulating plain concrete fracture Engineering MAZARS J.A description of micro-and macroscale Fracture Mechanics,2010,77(10):1577-603. damage of con te stru D].Engineering Fracture 04]WU J Y.XU S L Reconsideration on the elasti ,1986,25(5/6 :729737 theory for OLIVER J.FARIA R.Seismi 2013.50 damag (5).705805 D15]NGO M.IBRAHIMBEGOVIC A,BRANCHERIE D. B]LUBLINEAR J.OLIVER J.OLLER S,ONATE E.A Continuum damage model for the o-mechanical plastic-la model for concrete Intemational coupling in quasi-brittle materials].Engineering es.1989,25(3):299306 2013,503)170H78 LEE J,FENVES G L Plastic-dama el for cyel 61 李 学 究进展 Journal of Buildin Structure,2014.35(4:20-29.((in Chinese)) structures []International Joumnal of Solids 7】龙渝川,李正良.模拟混凝士滞回行为的各向异性 Structure,1998,35(14):1533+558. 损伤模型].工程力学,2011,28(8):62-69 WU JY,LIJ.FARIA R.An energy release rate-based LI Zhen amage mo nal of Solid&Structures. 2006,43(3/4):58 clie the Γ1 ies,20,288:6269.{in Chin ZHANG J.II J.Inv 8]KUPFER H,HILSDORF H K,RUSCH H.Behavior of rete for 3D simulation ]Engin oncrete under hiacial stresses ]Journal of ACl, Strictures,2012.44(1):122127 1969,66(8):656666 [8]RICHARD B.RAGUENEAU F. m dama u Beton.CEB-FIF mode mechanics based model for quasi-brittle material [SJ.Trowbridge,Wilshire subjected to cyclie and app Engineering plain ith of Building Materials.Lund University.1981 2012,34(1):114438. 61-65 [10]ALLICHE A.Damage model for fatigue loading of 1]BAZANTZ P,OH B H.Crack band theo concrete].Intemational Journal of Fatigue.004. e们. () Q B. SONG Y P.Da ageonstihutireofd 2] crete Joumal of Structural Engineering,ASCE, tional Joumal of Solids Structures,2004.41 1986,112(11):2462-2477. (11):31513166 23]车轶,郑新丰,王金金,等.单调荷作用下高强混 D2]VOYIADJIS G Z.TAQIEDDIN Z N.KATTAN P 1 欠寸效应研究门.建筑结构学拆 Anisotropie damage-plasticity model (CHE Yi,ZHE al Journal of Plasticity,2008,24 (10) 3]AL-RUB R K A.KIM S M.Computational application plast 2012,33(6):96-J02.(in Chinese)) 153 1994-2017China Academic Joumal Electronic Publishing House.All rights reserved.htp://www.enki.net
参 考 文 献 [1] MAZARS J. A description of micro-and macroscale damage of concrete structures[J]. Engineering Fracture Mechanics,1986,25( 5 /6) : 729-737. [2] CERVERA M, OLIVER J, FARIA R. Seismic evaluation of concrete dams via continumm damage models [J]. Earthquake Engineering & Structural Dynamics,1995,24( 9) : 1225-1245. [3] LUBLINEAR J,OLIVER J,OLLER S,ONATE E. A plastic-damage model for concrete[J]. International Journal of Solids & Structures,1989,25( 3) : 299-306. [4] LEE J,FENVES G L. Plastic-damage model for cyclic loading of concrete structures [J ]. Journal of Engineering Mechanics,ASCE,1998,124( 8) : 892-900. [5] FARIA R,OLIVER J,CERVERA M. A strain-based plastic viscous-damage model for massive concrete structures [J]. International Journal of Solids & Structures,1998,35( 14) : 1533-1558. [6] WU J Y,LI J,FARIA R. An energy release rate-based plastic-damage model for concrete[J]. International Journal of Solids & Structures,2006,43 ( 3 /4 ) : 583- 612. [7] ZHANG J, LI J. Investigation into Lubliner yield criterion of concrete for 3D simulation[J]. Engineering Structures,2012,44( 1) : 122-127. [8] RICHARD B,RAGUENEAU F. Continuum damage mechanics based model for quasi-brittle materials subjected to cyclic loadings: formulation,numerical implementation and applications [J]. Engineering Fracture Mechanics,2013,98( 1) : 383-406. [9] SCIARRA F M D. Hardening plasticity with nonlocal strain damage[J]. International Journal of Plasticity, 2012,34( 1) : 114-138. [10] ALLICHE A. Damage model for fatigue loading of concrete[J]. International Journal of Fatigue,2004, 26( 9) : 915-921. [11] L P Y,LI Q B,SONG Y P. Damage constitutive of concrete under uniaxial alternate tension-compression fatigue loading based on double bounding surfaces[J]. International Journal of Solids & Structures,2004,41 ( 11) : 3151-3166. [12] VOYIADJIS G Z,TAQIEDDIN Z N,KATTAN P I. Anisotropic damage-plasticity model for concrete[J]. International Journal of Plasticity,2008,24 ( 10 ) : 1946-1965. [13] AL-RUB R K A,KIM S M. Computational applications of a coupled plasticity-damage constitutive model for simulating plain concrete fracture [J]. Engineering Fracture Mechanics,2010,77( 10) : 1577-1603. [14] WU J Y,XU S L. Reconsideration on the elastic damage /degradation theory for the modeling of microcrack closure-reopening ( MCR ) effects [J]. International Journal of Solids & Structures,2013,50 ( 5) : 795-805. [15] NGO M,IBRAHIMBEGOVIC A,BRANCHERIE D. Continuum damage model for thermo-mechanical coupling in quasi-brittle materials[J]. Engineering Structures,2013,50 ( 3) : 170-178. [16] 李杰,任晓丹. 混凝土随机损伤力学研究进展[J]. 建筑结构学报,2014,35( 4) : 20-29. ( LI Jie,REN Xiaodan. Recent developments on stochastic damage mechanics for concrete [J]. Journal of Building Structures,2014,35( 4) : 20-29. ( in Chinese) ) [17] 龙渝川,李正良. 模拟混凝土滞回行为的各向异性 损伤 模 型[J]. 工 程 力 学,2011,28 ( 8 ) : 62-69. ( LONG Yuchuan, LI Zhengliang. An anisotropic damage model for simulating the hysteretic behavior of concrete under cyclic loading [J]. Engineering Mechanics,2011,28( 8) : 62-69. ( in Chinese) ) [18] KUPFER H,HILSDORF H K,RUSCH H. Behavior of concrete under biaxial stresses[J]. Journal of ACI, 1969,66( 8) : 656-666. [19] Comite Euro-International Du Beton. CEB-FIP model code 1990 ( design code) [S]. Trowbridge,Wilshire, UK: Thomas Telford,1993. [20] PETERSSON P E. Crack growth and development of fracture zones in plain concrete and similar materials [R]. Report No. TVBM-1006. Lund, Sweden: Division of Building Materials,Lund University,1981: 61-65. [21] BAZANT Z P,OH B H. Crack band theory for fracture of concrete[J]. Material & Structures,1983,16( 93) : 155-177. [22] REINHARDT H W, CORNELISSEN H A W, HORDIJK D A. Tensile tests and failure analysis of concrete[J]. Journal of Structural Engineering,ASCE, 1986,112 ( 11) : 2462-2477. [23] 车轶,郑新丰,王金金,等. 单调荷载作用下高强混 凝土梁受弯性能尺寸效应研究[J]. 建筑结构学报, 2012,33( 6) : 96-102. ( CHE Yi,ZHENG Xinfeng, WANG Jinjin,et al. Size effect on flexural behavior of reinforced high-strength concrete beams subjected to monotonic loading[J]. Journal of Building Structures, 2012,33( 6) : 96-102. ( in Chinese) ) 153