
第五章个体育种值估计—BLP法 教学目的与要求: 理解最佳线性无偏估计的基本原理与优点,了解BP的几种基本模 型。 重点: 最佳线性无偏估计的基本原理与优点 难点: 最佳线性无偏估计的基本原理与优点 BLP的几种基本模型 教学进程: 第一节有关基本知识 一、有关数学问题 1.随机变量:设x是一个随机变量,假设有n个,那么就会有x1x2 x3…xn个变量,如果一个x变量对应一个y值的话,也可以说每 一个x的方向是固定的,每一个y值的方向也相当于固定的,这时我 们就可以把这些变化的一个个的值用向量赖表示。 向量:具有方向性的变量。 矩阵:为了保证其方向性我们用矩阵来规范它。 期望值:相当于理论值与真实值对应。 当有几个随机变量时,他们这些变量可以用向量和矩阵描述出来。 x=kxx】或 那么它的方差一协方差都可以用矩阵描述出来 「Co',Co'2…Co'm 8… V.=V= Co'1Co'z… 6 CoaCo'n2… 62… 2.个体间家性遗传相关

(1)亲缘系数(个体遗传相关) 0,-号 ”Q+F)=∑)0+F) 对于一个群体,个体间遗传相关就可以用矩阵表示: am d2…am 注意:r= Cov(A,A,) 64()6,(y) 当它表示是两个个体之间家性相关的话r=C4A2 Co(A,A)=rd明 V= A(2 线性模型基础知识 模型:指描述观察值与影响观察值变异的各因子之间的关系的方程式 真实模型:准确的模拟观察值的变异性,几乎不可能。 理想模型:尽可能的接近真实模型 操作模型:用于实际统计分析的模型,它通常是理想模型的简化形式。 固定因子(固定效应):对于一个因子有意 识的抽取它的若干个 特定的水平,而研究 的目的就是对这些水 平的效应进行估计和 比较。 离散型随机因子(随机效应):如果一个因子的若 干水平被视为来自 该因子的所有水平 所构成的总体的随 机样本。研究的月的 就是通过该样本去

推断总体,则该因子 就是随机因子, 操作模型 它的不同水平的效 应就称为随机效应。 连续型 线性模型:在模型中所包含的各因子以相加的形式影响观察值,就 视为各因子与观察值之间的关系为线性关系。 1.数学方程式 线性模型使括2.方程式中随机变量的期望和方差、协方差 3.假设和约束条件 设某肉牛190一210日龄的体重资料,将日龄按每5天间隔分组, 190一210日龄可分为4组,欲分析不同日龄组对体重的影响。 建立的数学模型为:yg=μ+a,+eg y::第i个日龄组中的第j头肉牛的体重,可视为观察值的随机 变量。 4:总平均常数 a,:第i个月龄组的效应,它是固定效应 :剩余效应,也称为随机误差。 ①同一品种 约束条件: ②无母体效应 ③不考虑性别 ④饲养条件相同 y=198=+a,+ yn=204=4+e g=201=4+a1+e y21=203=4+a2+e2 y2=206=u+a2+e2 用向量和矩阵表示:y
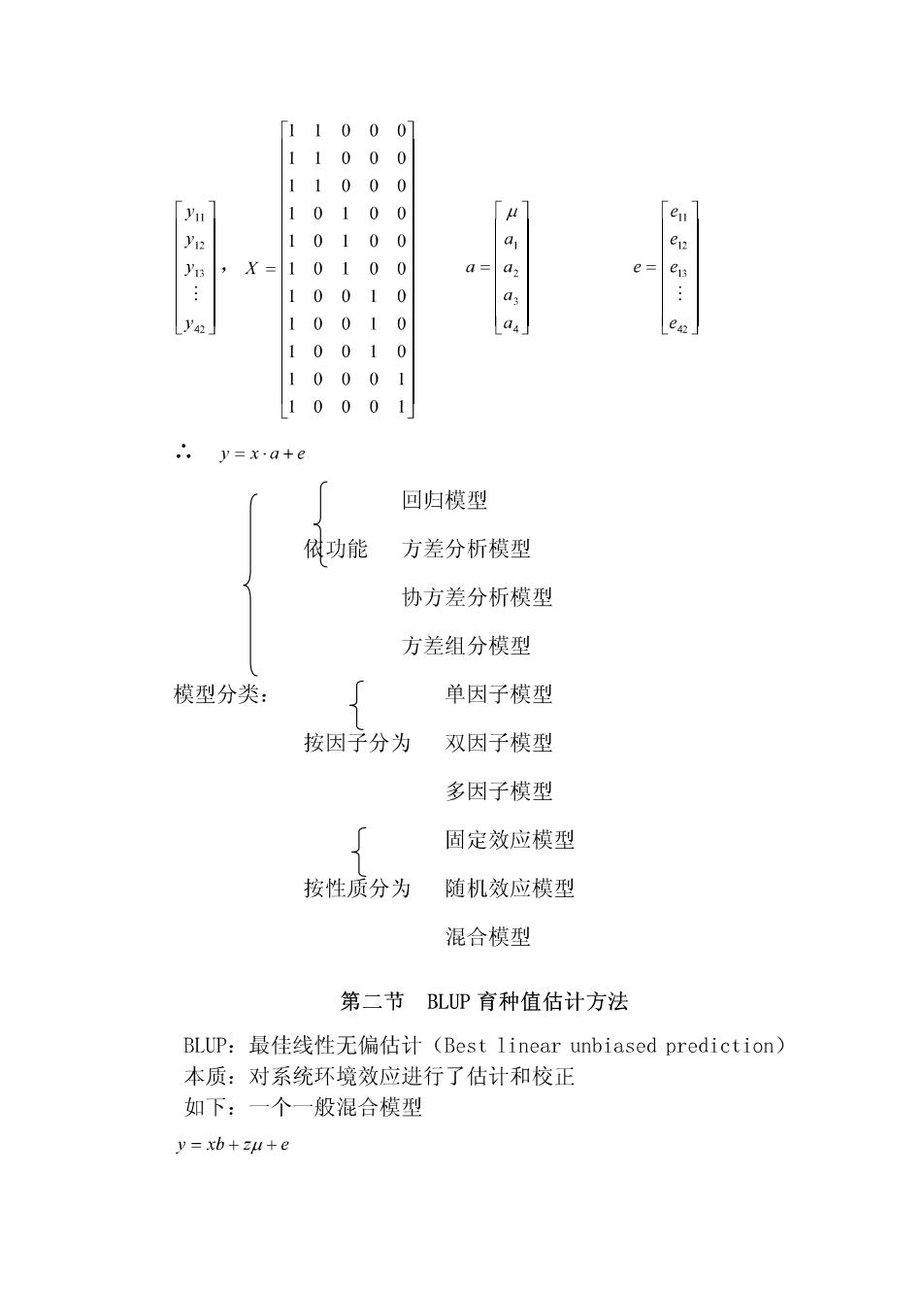
1000 1000 1 00 0100 010 X 101 00 es 1 0 01 0 001 e 001 0 10001 0001 .y=xate 回归模型 俄功能 方差分析模型 协方差分析模型 方差组分模型 模型分类: 单因子模型 按因子分为双因子模型 多因子模型 固定效应模型 按性质分为随机效应模型 混合模型 第二节BLUP育种值估计方法 BLUP:最佳线性无偏估计(Best linear unbiased prediction) 本质:对系统环境效应进行了估计和校正 如下:一个一般混合模型 y=xb+zu+e

y:观察值向量 b:固定效应向量 “:随机效应向量 e:随机误差向量 X,Z:为b和“的关联矩阵 模型中:需对b和“进行估 BLUP法:就是按照最佳线性无偏的原则去估计“和b。 最佳—估计值的误差方差最小 线性 估计值为观察值呈线性函数 无偏一估计值的数学期望等于真值 动物模型BL,P:根据观察值有无重复分为二种情况 无重复观察值时的动物模型BLUP 模型:y=6,+a+e b,—第i个系统环境效应 固定效应 a一个体育种值 随机效应 e- 一随机残差(由随机环境效应所致) 若有n个观察值,对s个个体育种值进行估计 则y=X+2a+e 最后 ]倒 模型:y=h,+a,+e -第i个牧场中的个体j的观察值 —第1个牧场的效应 第j个个体的育种值 一与观察值'对应的随机误差 写入矩阵:
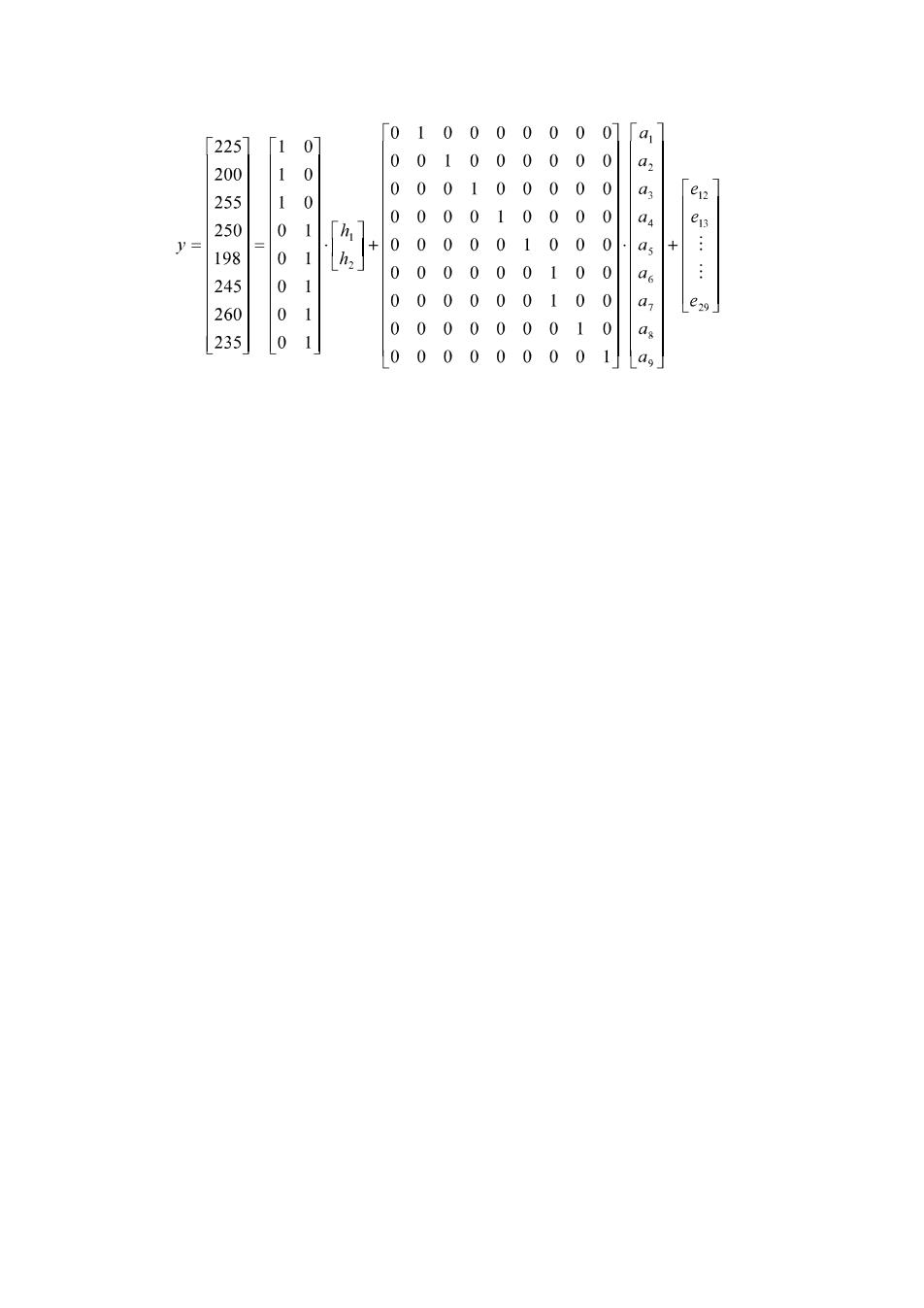
0 「225 1 0000000 oo 0 0 00 0 200 0 d; 0 0 0 0 0 1 e 0 0 0 598 h + 0 0 0 00 0 0 0 0