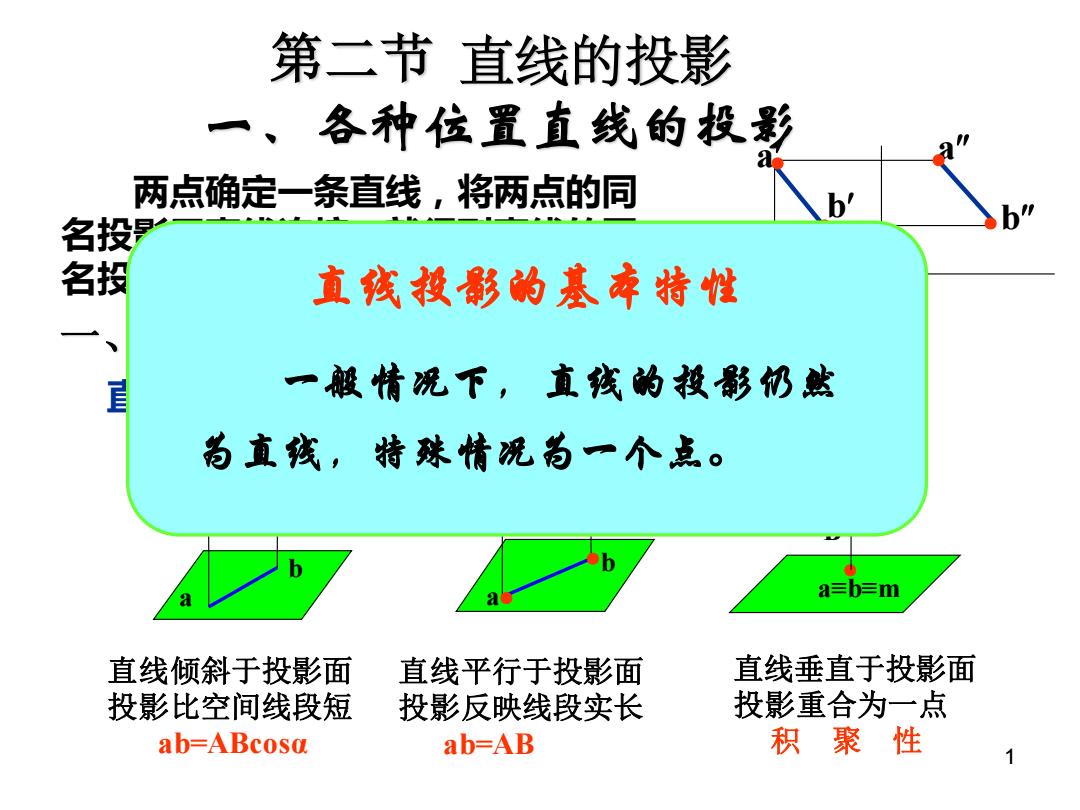
第二节直线的投影 一、各种位置直线的投影 两点确定一条直线,将两点的同 名投 名投 直线投影的基车特性 一般情况下,直孩的投影仍然 为直孩,特珠情况为一个点。 a≡b=m 直线倾斜于投影面 直线平行于投影面 直线垂直于投影面 投影比空间线段短 投影反映线段实长 投影重合为一点 ab=ABcosa ab=AB 积聚性
1 第二节 直线的投影 一、各种位置直线的投影 两点确定一条直线,将两点的同 名投影用直线连接,就得到直线的同 名投影。 直线对一个投影面的投影特性 一、直线的投影特性 A B ● ● ● ● a b 直线垂直于投影面 投影重合为一点 积 聚 性 直线平行于投影面 投影反映线段实长 ab=AB 直线倾斜于投影面 投影比空间线段短 ab=ABcosα ● ● A B ● ● a b α A M B● a≡b≡m ● ● ● a a a b b b ● ● ● ● ● ● 直线投影的基本特性 一般情况下,直线的投影仍然 为直线,特殊情况为一个点
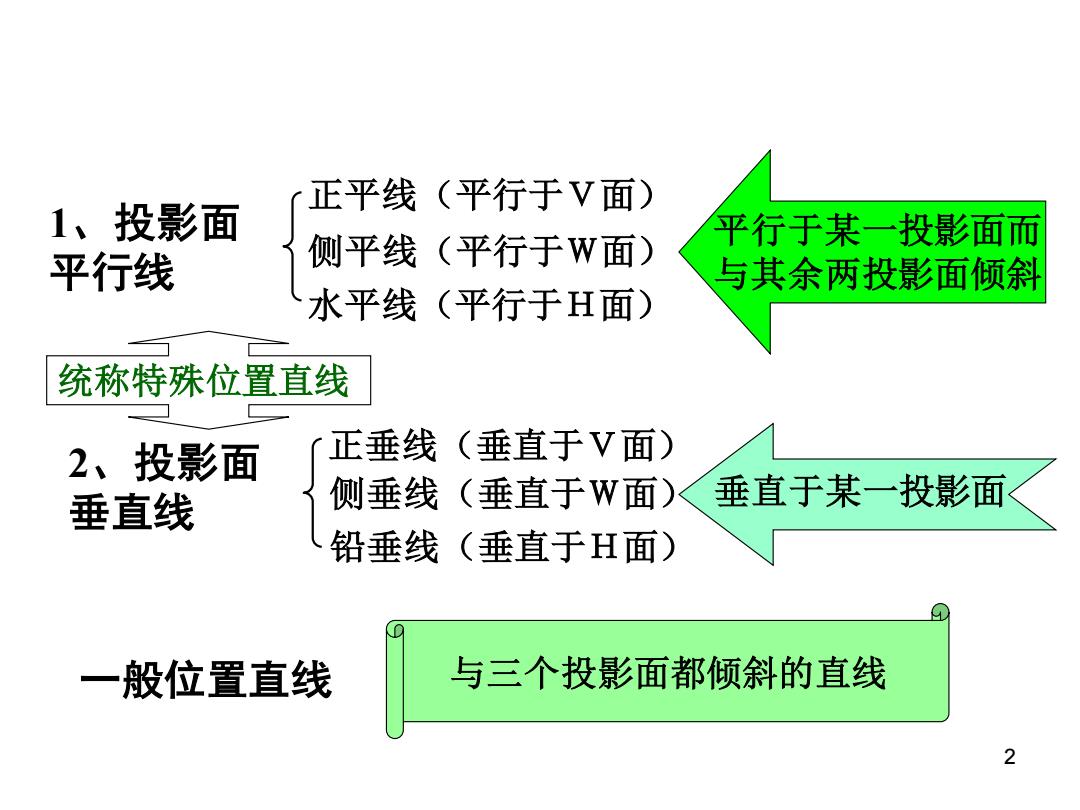
正平线(平行于V面) 1、投影面 平行于某一投影面而 平行线 侧平线(平行于W面) 与其余两投影面倾斜 水平线(平行于H面) 统称特殊位置直线 2、投影面 正垂线(垂直于V面) 垂直线 侧垂线(垂直于W面) 垂直于某一投影面 铅垂线(垂直于H面) 一般位置直线 与三个投影面都倾斜的直线 2
2 1、投影面 平行线 平行于某一投影面而 与其余两投影面倾斜 2、投影面 垂直线 正平线(平行于V面) 侧平线(平行于W面) 水平线(平行于H面) 正垂线(垂直于V面) 侧垂线(垂直于W面) 铅垂线(垂直于H面) 一般位置直线 与三个投影面都倾斜的直线 统称特殊位置直线 垂直于某一投影面
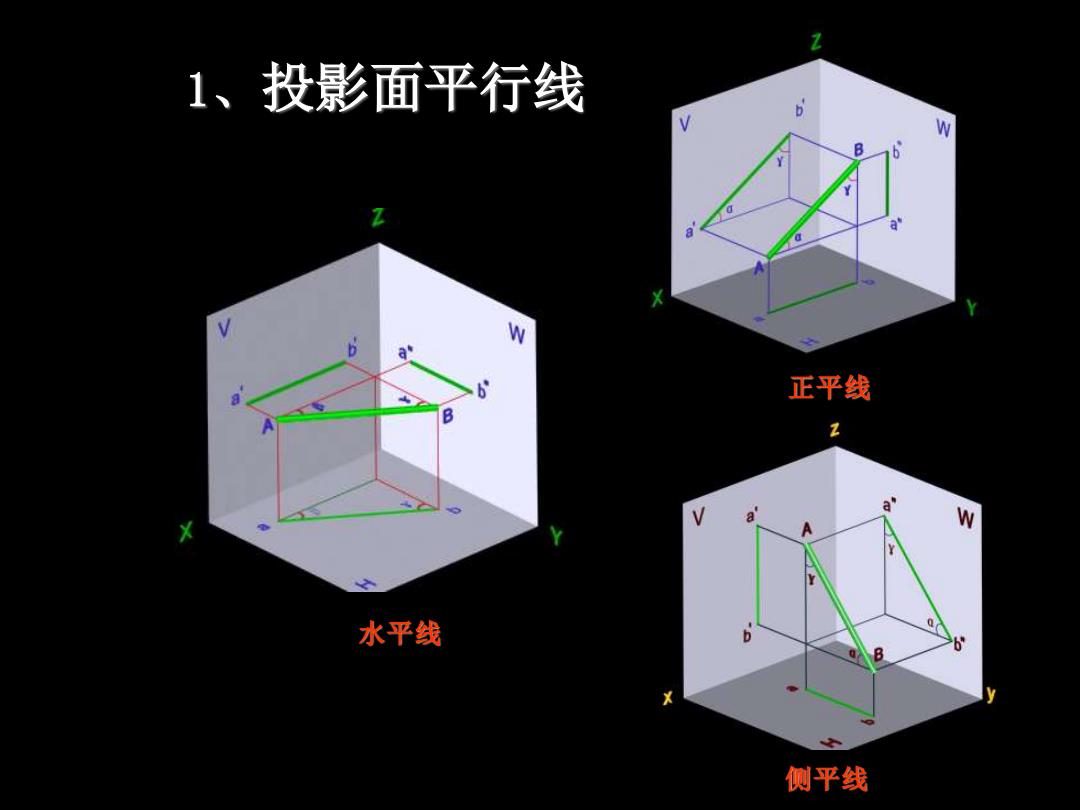
1、投影面平行线 Z 正平线 水平线 6 侧平线
3 1、投影面平行线 水平线 正平线 侧平线
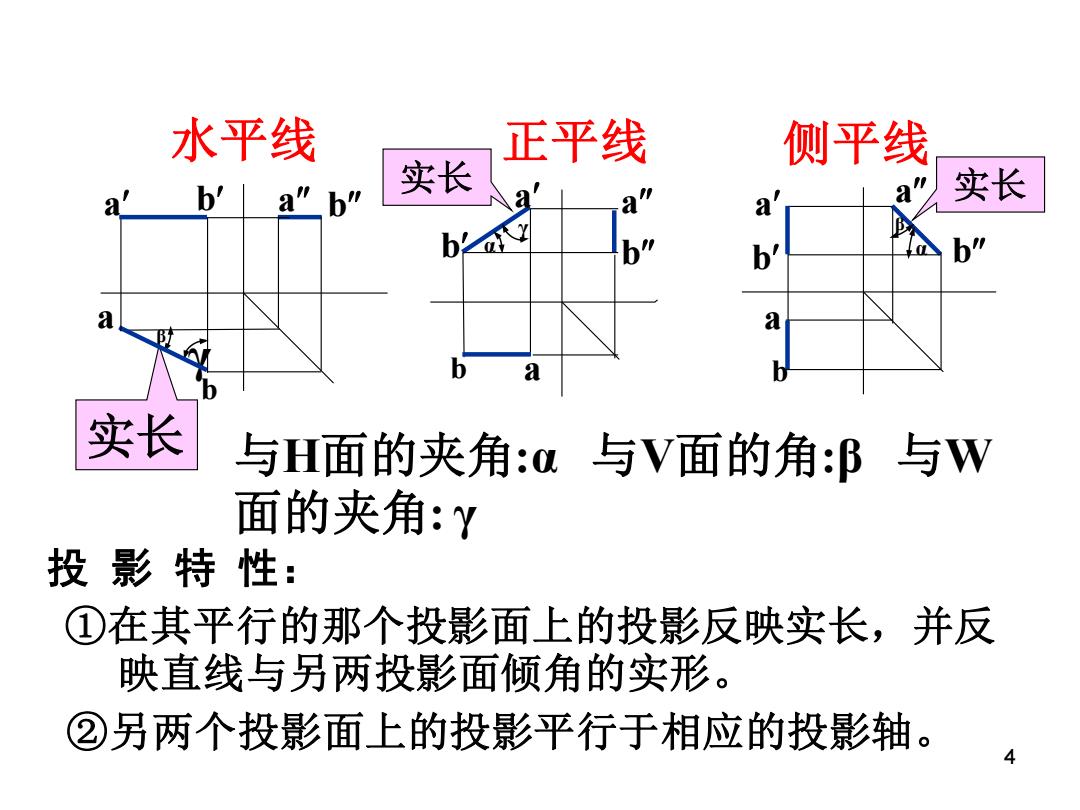
水平线 正平线 侧平线 b'a"b" 实长 a 实长 b a y b" b' b" a a b a 实长 与H面的夹角:a与V面的角:P与W 面的夹角:Y 投影特性: ①在其平行的那个投影面上的投影反映实长,并反 映直线与另两投影面倾角的实形。 ②另两个投影面上的投影平行于相应的投影轴
4 b a b a a b b a a b b a ①在其平行的那个投影面上的投影反映实长,并反 映直线与另两投影面倾角的实形。 ②另两个投影面上的投影平行于相应的投影轴。 水平线 正平线 侧平线 γ 投 影 特 性: 与H面的夹角:α 与V面的角:β 与W 面的夹角: γ 实长 实长 实长 β γ α α β b a a a b b
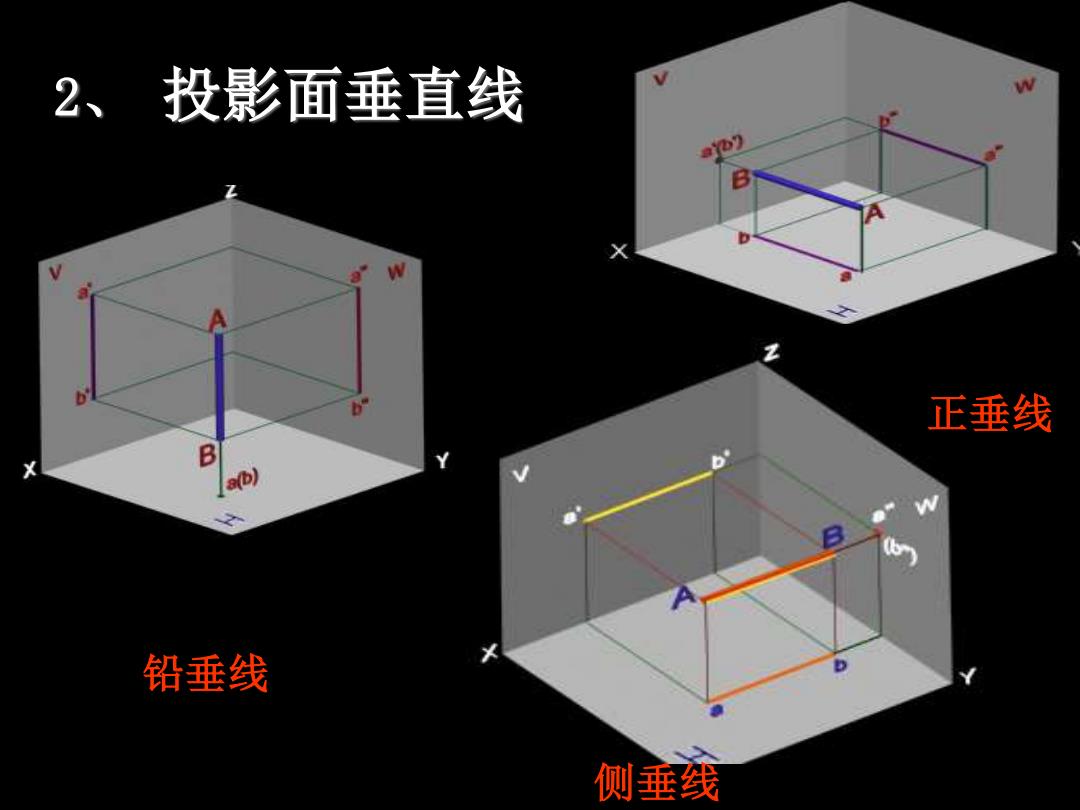
2、投影面垂直线 W 正垂线 B s(b) 铅垂线 D 侧垂线
5 2、 投影面垂直线 铅垂线 正垂线 侧垂线
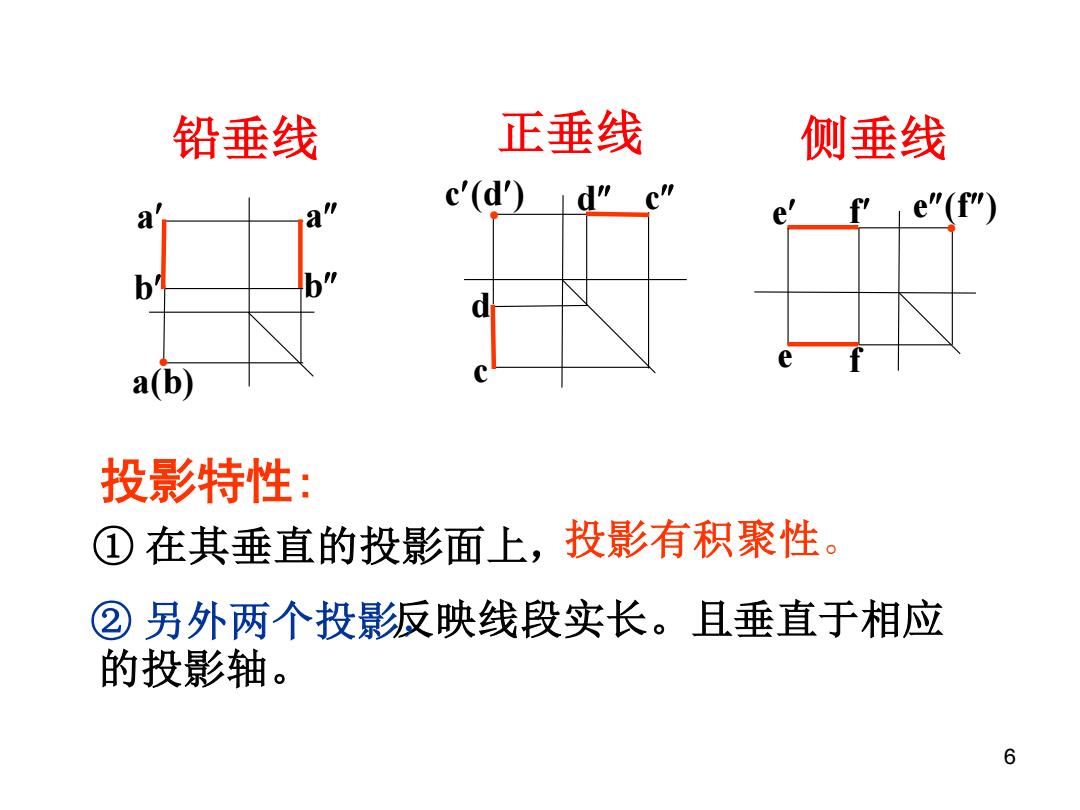
铅垂线 正垂线 侧垂线 a" a” c'(d')d"c" e e"(f) b b" d a(b) 投影特性: ①在其垂直的投影面上,投影有积聚性。 ②另外两个投影饭映线段实长。且垂直于相应 的投影轴。 6
6 反映线段实长。且垂直于相应 的投影轴。 铅垂线 正垂线 侧垂线 ② 另外两个投影, ① 在其垂直的投影面上,投影有积聚性。 投影特性: ● c(d) c d d c ● a b a(b) a b ● e f e f e(f)
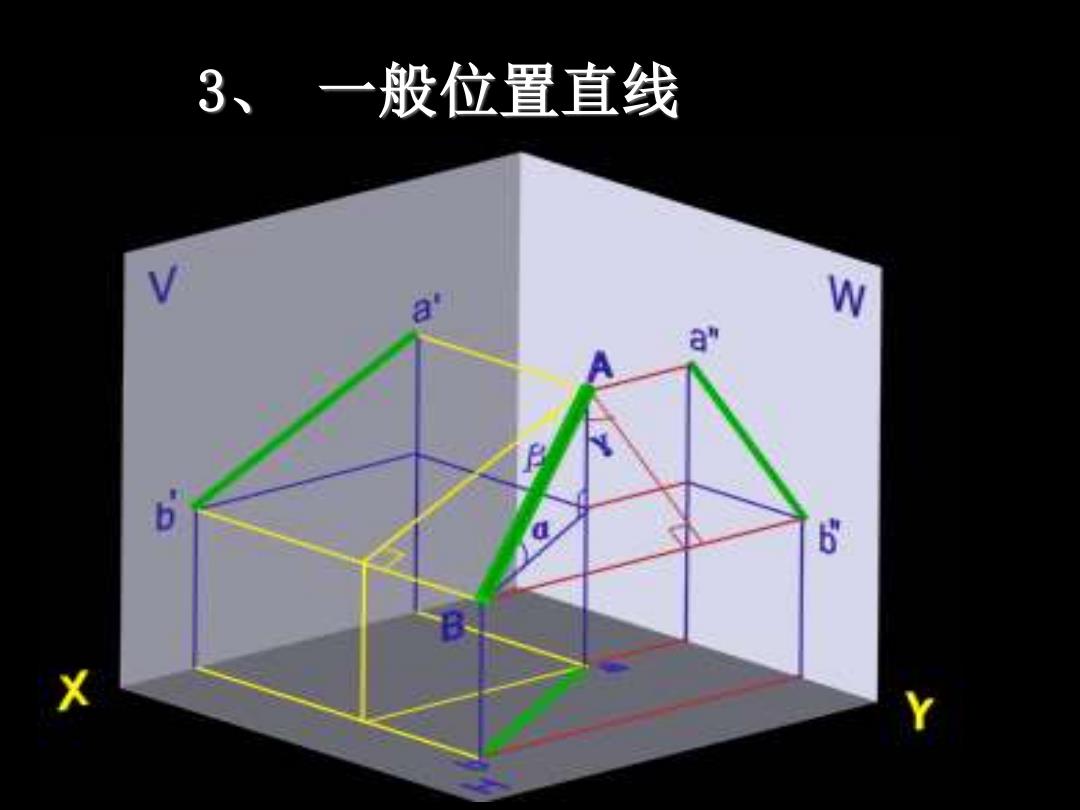
3、一般位置直线 a" 6
7 3、 一般位置直线
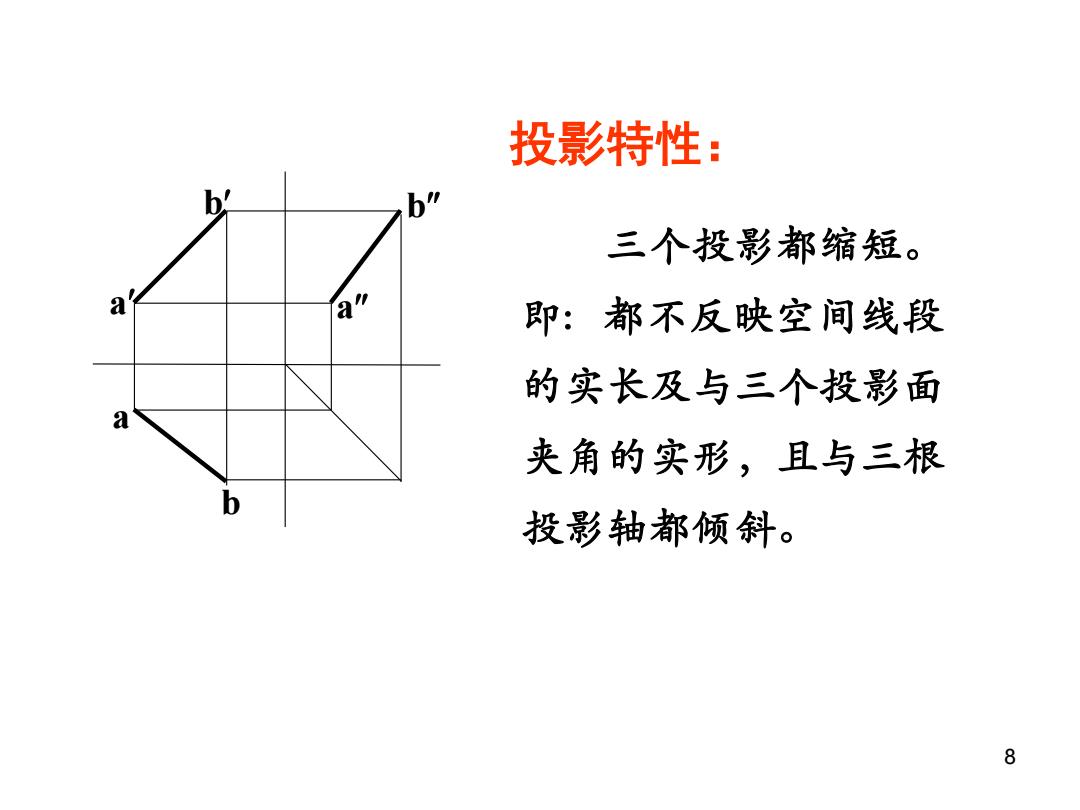
投影特性: b 三个投影都缩短。 a an 即:都不反映空间线段 的实长及与三个投影面 a 夹角的实形,且与三根 b 投影轴都倾斜。 8
8 投影特性: 三个投影都缩短。 即: 都不反映空间线段 的实长及与三个投影面 夹角的实形,且与三根 投影轴都倾斜。 a b b a b a
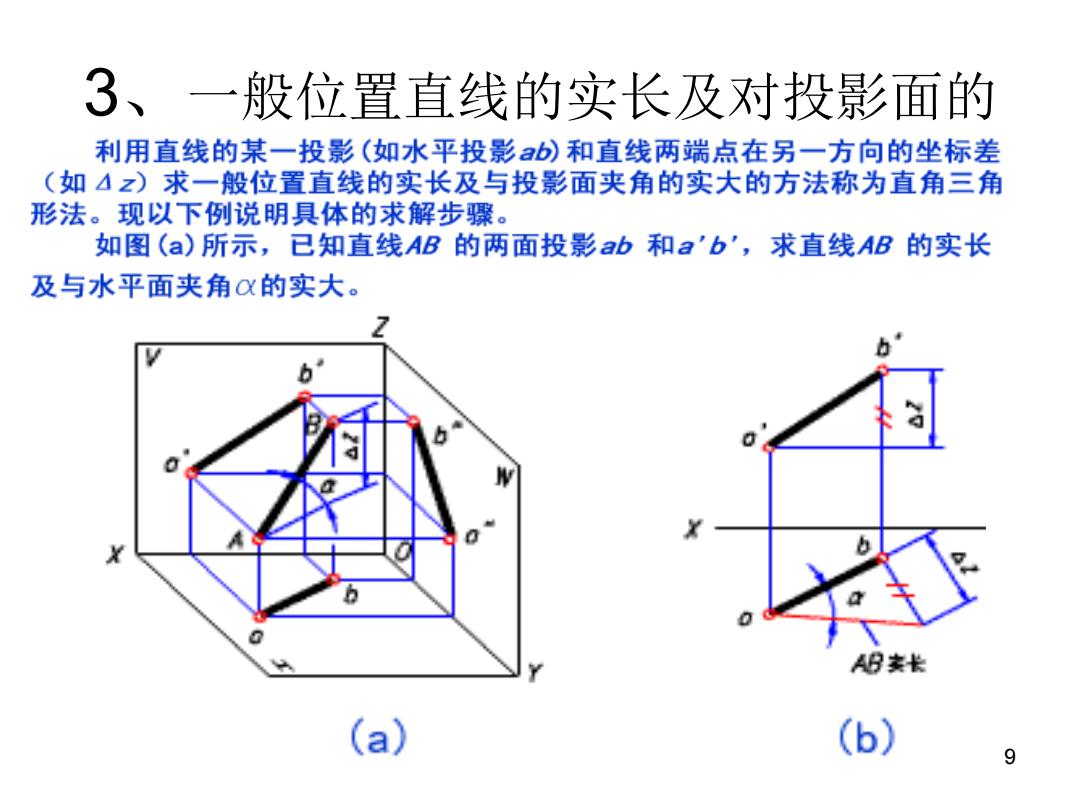
3、一般位置直线的实长及对投影面的 利用直线的某一投影(如水平投影ab)和直线两端点在另一方向的坐标差 (如4z)求一般位置直线的实长及与投影面夹角的实大的方法称为直角三角 形法。现以下例说明具体的求解步骤。 如图(a)所示,已知直线AB的两面投影ab和a'b',求直线AB的实长 及与水平面夹角0的实大。 b 0 AB炭长 (a) (b) 9
9 3、一般位置直线的实长及对投影面的 倾角
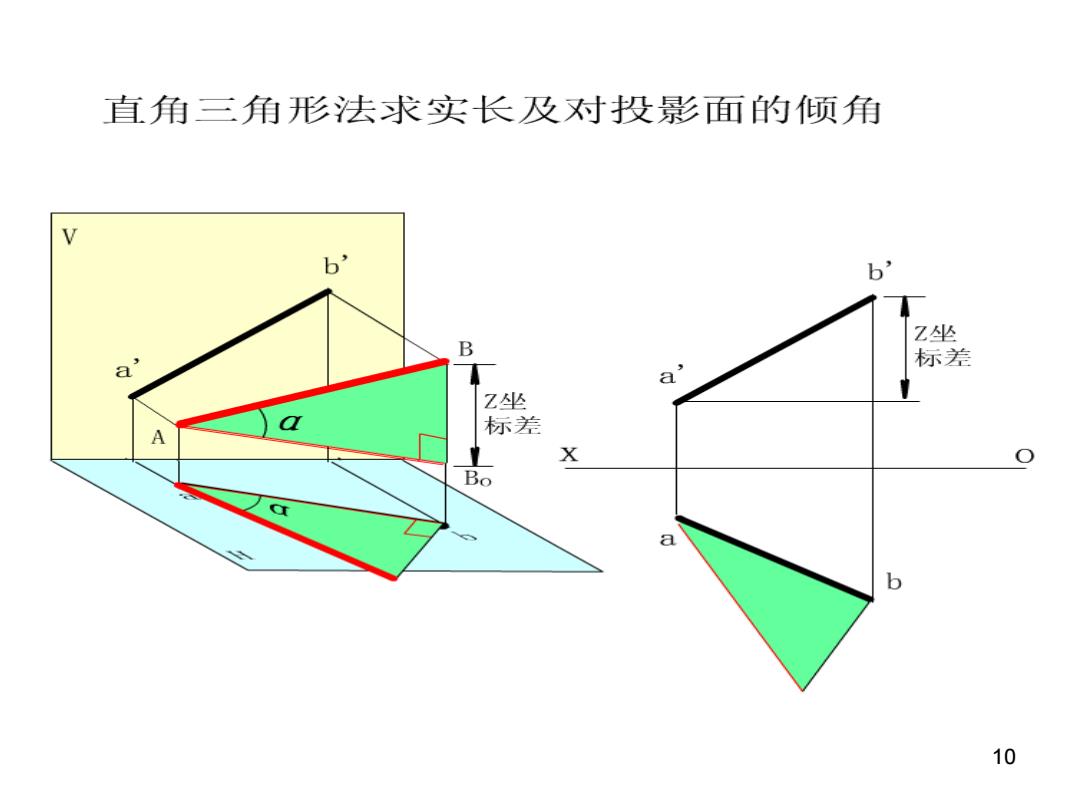
直角三角形法求实长及对投影面的倾角 6 b' Z坐 B 标差 Z坐 a A 标差 X 0 Bo 6 10
10