
《算法分析与设计》课程教学大纲 (Analysis Design of Algorithm)Teaching Outline 一、课程基本信息 课程代码:16158603 课程名称:算法分析与设计 英文名称:Analysis&Design of Algorithm 课程类别:专业课 学 时:48(课堂教学36,实验教学12) 学分:3 适用对象:计算机科学与技术专业本科生 考核方式:考试 先修课程:C或JAVA语言、数据结构 二、课程简介 中文简介 《算法分析与设计》是软件开发人员必修专业课,软件的效率和稳定性取决于软 件中所采用的算法技术:对于一般程序员和软件类专业学生,学习算法设计与分析课 程,可以开阔编程思路,找到最优问题的高效求解算法,提高程序的时间效率和空间 效率 英文简介 Analysis and Design of Algorithms is a compulsory specialty course for software developers.Effic ency and stability of software depends on algorithm-techniques used.For common coders and software relative students,learning this course could expand their programming vision and help them programming high quality codes.finding out the optimization solving algorithm in time and space 课程性质与教学目的 通过对常用的、有代表性的算法的研究,让学生理解并掌握算法设计的基本技术。 培养学生分析算法复杂度的初步能力,锻炼其逻辑思维能力和想象力,理解问题的难 度分类、并使之掌握算法理论的基本要点,了解算法理论的基本框架,并能够从辩证 唯物主义告诉我们的“真理是客观的,同时又是绝对的和相对的”角度,深入理解计 算机科学与 支不专 业中的NF 全理论体系。站在 学生具备 算法 术和相 的知识,去解决系统开发过程中的实际问题,从而培养学生的独立科研的能力和理论 联系实践的能力。 四、教学内容及要求
1 《算法分析与设计》课程教学大纲 《Analysis & Design of Algorithm》Teaching Outline 一、课程基本信息 课程代码:16158603 课程名称:算法分析与设计 英文名称:Analysis & Design of Algorithm 课程类别:专业课 学 时:48(课堂教学 36,实验教学 12) 学 分:3 适用对象: 计算机科学与技术专业本科生 考核方式:考试 先修课程:C 或 JAVA 语言、数据结构 二、课程简介 中文简介 《算法分析与设计》是软件开发人员必修专业课,软件的效率和稳定性取决于软 件中所采用的算法技术;对于一般程序员和软件类专业学生,学习算法设计与分析课 程,可以开阔编程思路,找到最优问题的高效求解算法,提高程序的时间效率和空间 效率。 英文简介 Analysis and Design of Algorithms is a compulsory specialty course for software developers. Effici ency and stability of software depends on algorithm-techniques used. For common coders and software relative students, learning this course could expand their programming vision and help them programming high quality codes, finding out the optimization solving algorithm in time and space. 三、课程性质与教学目的 通过对常用的、有代表性的算法的研究,让学生理解并掌握算法设计的基本技术。 培养学生分析算法复杂度的初步能力,锻炼其逻辑思维能力和想象力,理解问题的难 度分类、并使之掌握算法理论的基本要点,了解算法理论的基本框架,并能够从辩证 唯物主义告诉我们的“真理是客观的,同时又是绝对的和相对的”角度,深入理解计 算机科学与技术专业中的 NP 完全理论体系。站在。使学生具备运用算法技术和相关 的知识,去解决系统开发过程中的实际问题,从而培养学生的独立科研的能力和理论 联系实践的能力。 四、教学内容及要求

第一章算法引论 (一)目的与要求 掌握算法,算法复杂度的基本概念,及时间复杂度的估算方法。 (二)教学内容 第一节算法与程序 1.主要内容 算法特征、算法与程序的区别 2.基本念和知识点 算法的定义、算法的五大特徊 程序+数据结构+算法=编程 3.问题与应用 思考:只要是计算机程序,便是算法的实现吗? 第二节算法描述 1.主要内容 算法的表示与规范化描述方法 2.基本概念和知识点 Seduocode,算法描术的基本格式 3.问题与应用 思考 :算法描述到什么程度,其描述粒度便是合适的? 第三节算法复杂性分析 1.主要内容 算法的时间复杂性、空间复杂性,渐进表达式 2.基本概念和知识点 算法的时间复杂性、空间复杂性,渐进表达式 3.问题与应用 掌握算法复杂度的基本概念及时间复杂度的估算方法。 函数的渐进表达式。 在算法复杂性分析的教学中,要重点介绍时间复杂性从O)逐渐演化到 O2),也即“从易到难”的过程,并引出对“一分为二,这是个普遍的现象,这就 是辩证法。”(《毛泽东选集》第5卷第498页)这个哲学思想在计算机算法设计中的 体现、在算法时间复杂性研究和讨论中的体现。 (三)教学方法与手段 课堂讲授为主,结合课堂分组讨论。 第二章递归与分治策略 (一)目的与要求 1,掌握递归的概念,学会用递归方法解决实际问题: 2.熟练学握利用分治法解决问题的基本思想,会用某高级语言对算法进行描述, 2
2 第一章 算法引论 (一)目的与要求 掌握算法,算法复杂度的基本概念,及时间复杂度的估算方法。 (二) 教学内容 第一节 算法与程序 1.主要内容 算法特征、算法与程序的区别 2.基本概念和知识点 算法的定义、算法的五大特征 程序+数据结构+算法=编程 3.问题与应用 思考:只要是计算机程序,便是算法的实现吗? 第二节 算法描述 1.主要内容 算法的表示与规范化描述方法 2.基本概念和知识点 Seduocode,算法描述的基本格式 3.问题与应用 思考:算法描述到什么程度,其描述粒度便是合适的? 第三节 算法复杂性分析 1.主要内容 算法的时间复杂性、空间复杂性,渐进表达式 2.基本概念和知识点 算法的时间复杂性、空间复杂性,渐进表达式 3.问题与应用 掌握算法复杂度的基本概念及时间复杂度的估算方法。 函数的渐进表达式。 在算法复杂性分析的教学中,要重点介绍时间复杂性从 O(1)逐渐演化到 O(2^n),也即“从易到难”的过程,并引出对“一分为二,这是个普遍的现象,这就 是辩证法。”(《毛泽东选集》第 5 卷第 498 页)这个哲学思想在计算机算法设计中的 体现、在算法时间复杂性研究和讨论中的体现。 (三) 教学方法与手段 课堂讲授为主,结合课堂分组讨论。 第二章 递归与分治策略 (一)目的与要求 1. 掌握递归的概念,学会用递归方法解决实际问题; 2. 熟练掌握利用分治法解决问题的基本思想,会用某高级语言对算法进行描述

并对算法复杂度(时间和空间)进行分析。 (二)教学内容 第一节递归的概念 1.主要内容 递归概念,递归的程序实现 2.基本概念和知识点 递归思想 3.问题与应用 从易到难举例:指数算法、阶乘算法:汉诺塔问题 第二节分治法的基本思想 1。主要内容 分治法基本思想、子问题与子问题相互独立性 2.基本概念和知 识点 分治思想及其应 3.问题与应用 二分搜索技术,大整数乘法 第三节应用实例 主要内容 矩阵乘法,棋盘覆盖,合并排序,快速排序,线性时间选择 2.基本概念和知识点 各类应用实例的分治思维方法 3。问题与应用 掌握递归的概念 学会用递归方法解决实际问题,熟练掌握利用分治法解法 问题的基本思想 会用某高级语言对算法进行描述,并对算法复杂度(时间 和空间)进行分析。 算法设计:CHESS COVERING问题、子段和问题 (三)课后练习 Han o塔问题的非递归算法 (四)教学方法与手段 课堂讲授为主,结合课堂分组讨论。 第三章动态规划 (一)目的与要 熟练掌握利用动态规划方法解决问题的基本思想 2.学会如何将问题化为子问题的方法: 3.能对具体问题写出正确的递推公式。 (二)教学内容 第一节动态规划算法的基本要素 1.主要内容 3
3 并对算法复杂度(时间和空间)进行分析。 (二)教学内容 第一节 递归的概念 1. 主要内容 递归概念,递归的程序实现 2. 基本概念和知识点 递归思想 3. 问题与应用 从易到难举例:指数算法、阶乘算法;汉诺塔问题 第二节 分治法的基本思想 1.主要内容 分治法基本思想、子问题与子问题相互独立性 2.基本概念和知识点 分治思想及其应用 3.问题与应用 二分搜索技术,大整数乘法 第三节 应用实例 1.主要内容 矩阵乘法,棋盘覆盖,合并排序,快速排序,线性时间选择 2.基本概念和知识点 各类应用实例的分治思维方法 3.问题与应用 掌握递归的概念,学会用递归方法解决实际问题,熟练掌握利用分治法解决 问题的基本思想,会用某高级语言对算法进行描述,并对算法复杂度(时间 和空间)进行分析。 算法设计:CHESS COVERING 问题、子段和问题 (三)课后练习 Hanoi 塔问题的非递归算法。 (四)教学方法与手段 课堂讲授为主,结合课堂分组讨论。 第三章 动态规划 (一)目的与要求 1.熟练掌握利用动态规划方法解决问题的基本思想; 2.学会如何将问题化为子问题的方法; 3.能对具体问题写出正确的递推公式。 (二)教学内容 第一节 动态规划算法的基本要素 1. 主要内容

动态规划的基本要素、动态规划思想、动态规划算法步骤 2.基本概念和知识点 动态规划思想、最优子结构性质、子问题重叠性质、动态规划算法的时间复 杂性分析 3.问题与应用 思考:动态规划与分治法思想的区别与比较 通过对动态规划和分治法思想这两种算法思想的比较,从算法效率的角 度,引出“科学是第 生产力 这个重要诊断!并从生产力的“劳动者、劳 动工具和劳动对象”这三大要素中,把计算机这个劳动工具进一步理解到算 法层面。 第二节最长公共子序列 1.主要内容 LCS问题的定义、LCS问题的DP求解思路 2,基本概念和知识点 LCS、自底向上的编程思维、算法时间复杂性分析 3,问题与应用 串的各种运算及其比较 第三节矩阵连乘问题 1.主要内容 矩阵连乘问题 2.基本概念和知识点 矩阵连乘、算法时间复杂性分析 问题与应用 矩阵连乘问题的算法设计 第四节其他应用 4.主要内容 最大子段和,凸多边形最优三角剖分,多边形游戏,图像压缩,电路布线, 流水作业调度 0-1背包问题 5.基本概念和知识点 各类问题的定义、DP思想的递推方程 6.问题与应用 如何设计能够应用DP算法的递推方程? (三)课后练习 Triangle Problem的DP算法设计。 算法设计:TRIANGLE问题、LCS问题、数塔问题、矩阵连乘问题,等等 (四)教学方法与手段 课堂讲授为主,结合分组课堂讨论。 第四章贪心算法 4
4 动态规划的基本要素、动态规划思想、动态规划算法步骤 2. 基本概念和知识点 动态规划思想、最优子结构性质、子问题重叠性质、动态规划算法的时间复 杂性分析 3. 问题与应用 思考:动态规划与分治法思想的区别与比较 通过对动态规划和分治法思想这两种算法思想的比较,从算法效率的角 度,引出“科学是第一生产力”这个重要诊断!并从生产力的“劳动者、劳 动工具和劳动对象”这三大要素中,把计算机这个劳动工具进一步理解到算 法层面。 第二节 最长公共子序列 1.主要内容 LCS 问题的定义、LCS 问题的 DP 求解思路 2. 基本概念和知识点 LCS、自底向上的编程思维、算法时间复杂性分析 3. 问题与应用 串的各种运算及其比较 第三节 矩阵连乘问题 1.主要内容 矩阵连乘问题 2. 基本概念和知识点 矩阵连乘、算法时间复杂性分析 3. 问题与应用 矩阵连乘问题的算法设计 第四节 其他应用 4. 主要内容 最大子段和,凸多边形最优三角剖分,多边形游戏,图像压缩,电路布线, 流水作业调度,0-1 背包问题 5. 基本概念和知识点 各类问题的定义、DP 思想的递推方程 6. 问题与应用 如何设计能够应用 DP 算法的递推方程? (三)课后练习 Triangle Problem 的 DP 算法设计。 算法设计:TRIANGLE 问题、LCS 问题、数塔问题、矩阵连乘问题,等等 (四)教学方法与手段 课堂讲授为主,结合分组课堂讨论。 第四章 贪心算法

(一)目的与要求 1.掌握利用贪心算法解决问题的基本思想: 2.会用某高级语言编写用贪心算法解决问题的程序,并能对算法的复杂度 可靠性进行分析。 (二)教学内容 第一节贪心算法的基本要素 1。主要内容 贪心选择性质、最优子结构性质 2基木概令和知识占 贪心选择、最优子结构、算法时间复杂性分析 3.问颗与应用 贪心算法与动态规划算法的差异 第二节单源最短路径 1.主要内容 算法基本思想、算法的正确性和计算复杂性 2.基本概念和知识点 单源最短路径、算法时间复杂性分析 3 问题与应用 单源最短路径的程序实现 第三节其他应用 1.主要内 活动安排问题,最优装载,哈夫曼编码,最小生成树,多机调度 2. 基本概念和知识点 问题的描述与理解 3.问题与应用 实现以上各类问题的程序、分析各类问题的算法时间复杂性 贪心算法在问题具有什么特征下,才是正确的? (三)实践环节与课后练习 活动安排问题的贪心选择算法。 (四)教学方法与手段 课堂讲授为主,结合课堂分组讨论。 笋五音可湖法 (一)目的与要求 1,掌握利用回溯法解决问题的基本思想: 2,会用回溯法解决:个皇后问题,图的m着色问题,批处理作业调度问题 等,并能准确地分析回溯法的效率及稳定性。 (一)教学内容 第一节回溯法思想 5
5 (一)目的与要求 1.掌握利用贪心算法解决问题的基本思想; 2.会用某高级语言编写用贪心算法解决问题的程序,并能对算法的复杂度, 可靠性进行分析。 (二)教学内容 第一节 贪心算法的基本要素 1. 主要内容 贪心选择性质、最优子结构性质 2. 基本概念和知识点 贪心选择、最优子结构、算法时间复杂性分析 3. 问题与应用 贪心算法与动态规划算法的差异 第二节 单源最短路径 1.主要内容 算法基本思想、算法的正确性和计算复杂性 2. 基本概念和知识点 单源最短路径、算法时间复杂性分析 3. 问题与应用 单源最短路径的程序实现 第三节 其他应用 1.主要内容 活动安排问题,最优装载,哈夫曼编码,最小生成树,多机调度。 2. 基本概念和知识点 问题的描述与理解 3. 问题与应用 实现以上各类问题的程序、分析各类问题的算法时间复杂性 贪心算法在问题具有什么特征下,才是正确的? (三)实践环节与课后练习 活动安排问题的贪心选择算法。 (四)教学方法与手段 课堂讲授为主,结合课堂分组讨论。 第五章 回溯法 (一)目的与要求 1.掌握利用回溯法解决问题的基本思想; 2.会用回溯法解决:n 个皇后问题,图的 m 着色问题,批处理作业调度问题 等,并能准确地分析回溯法的效率及稳定性。 (二)教学内容 第一节 回溯法思想

1.主要内容 回溯法的算法思想及其框架 2.基本概念和知识点 回溯法、回溯法的算法思想及其框架 3.问题与应用 旅行售货员问题 第二节回溯法应用 1.主要内容 n个皇后问题,最大团问题,图的m着色问题,旅行售货员问题,圆排列问 题,连续邮资问题,电路板排列问题。 2.基本概念和知识点 各类问题的理解、回溯法思想的应用 问题与应用 掌握利用回溯法解决问题的基本思想。 (三)课后练习 TP问题的回湖法程序设计。 (四)教学方法与手段 课堂讲授为主,结合课堂分组讨论 第六章分支限界法 (一)目的与要求 1.掌握利用分支限界法解决问题的基本思想: 2能用多种不同方法解法同一问题,并分析各方法的效率。 (一)教学内容 第一节 分支限界法的算法思想 1.主要内容 分支限界法的算法思想、解决问题的算法时间复杂性特征 2.基本概念和知识点 分支限界法的算法思想、剪枝限界 3.问题与应用 从时间复杂性来说 一般是什么类型的问题需要用分支限界法? 分支限界法 回溯法的异同? 第二节01背包问题 1,主要内容 0-1背包问题的理解、用分支限界法求解 2基本概今和知识占 0-1背包问题 背包问题 问题与应用 01背包问题与背包问题的异同点?两个问题的时间复杂性分析? 6
6 1. 主要内容 回溯法的算法思想及其框架 2. 基本概念和知识点 回溯法、回溯法的算法思想及其框架 3. 问题与应用 旅行售货员问题 第二节 回溯法应用 1.主要内容 n 个皇后问题,最大团问题,图的 m 着色问题,旅行售货员问题,圆排列问 题,连续邮资问题,电路板排列问题。 2. 基本概念和知识点 各类问题的理解、回溯法思想的应用 3. 问题与应用 掌握利用回溯法解决问题的基本思想。 (三)课后练习 TSP 问题的回溯法程序设计。 (四)教学方法与手段 课堂讲授为主,结合课堂分组讨论。 第六章 分支限界法 (一)目的与要求 1. 掌握利用分支限界法解决问题的基本思想; 2. 能用多种不同方法解法同一问题,并分析各方法的效率。 (二)教学内容 第一节 分支限界法的算法思想 1. 主要内容 分支限界法的算法思想、解决问题的算法时间复杂性特征 2. 基本概念和知识点 分支限界法的算法思想、剪枝限界 3. 问题与应用 从时间复杂性来说,一般是什么类型的问题需要用分支限界法? 分支限界法与回溯法的异同? 第二节 0-1 背包问题 1.主要内容 0-1 背包问题的理解、用分支限界法求解 2. 基本概念和知识点 0-1 背包问题、背包问题 3. 问题与应用 0-1 背包问题与背包问题的异同点?两个问题的时间复杂性分析?

第三节其他应用 1.主要内容 单源最短路径,布线问题,批处理作业调度问题。 2.基本概今和知识占 各类问题的定义、算法应用 问题与应用 用多种方法求解 (三)实践环节 01背包问题的分支限界法算法实现。 (四)教学方法与手段 课堂讲授为 结合课堂分组讨论 第七章NP完全性理论与近似算法 (一)目的与要求 1.了解NPC理论中的假设条件,并能够从“真理的相对性”角度,来阐述 NP完全之所以能够成立的前提假设: 2· 掌握P类与N 题的划分 利用近似算法解决问题的基本思想,能对其可靠性进行分。 (二)教学内容 第一节问题分类 1. 主要内容 计算模型:确定性图灵机DTM、非确定性图灵机NDTM 问题的分类:P类与NP类问题、不可解问题 2.基本概今和知识点 DTM与NDTM P类与NP类问题 此内容的教学过程中,要介绍一下计算机之父A.MTui血g,及等价于计算机 界的NOBEL奖地位的“图灵奖”得主中,于2000年获得图灵奖的华人姚期 智教授,计算理论包括伪随机数生成、密码学与通信复杂度的突出贡献,美 国计算机协会(ACM)把2000年度的图灵奖授予他。姚期智是图灵奖创立 以来首位获奖的亚裔学者,也是迄今为止获此殊荣的唯一华裔计算机科学家。 姚期智教授放弃了自己在美国优厚的工作待遇,甚至是不惜变卖自己在美国 的房产回国,充分展现了中华学子的爱国情怀!同时强调:姚期智教授在计 算理论中所做出的突出贡献,充实和完普了NP完全理论的知识体系。 3.问题与知识要点 问题及其分类,问题的难度与时间复杂性关系、NP类问题的证明 第二节NP完全问题与NP-hard问题 1.主要内容 7
7 第三节 其他应用 1.主要内容 单源最短路径,布线问题,批处理作业调度问题。 2. 基本概念和知识点 各类问题的定义、算法应用 3. 问题与应用 用多种方法求解 (三)实践环节 0-1 背包问题的分支限界法算法实现。 (四)教学方法与手段 课堂讲授为主,结合课堂分组讨论。 第七章 NP 完全性理论与近似算法 (一)目的与要求 1.了解 NPC 理论中的假设条件,并能够从“真理的相对性”角度,来阐述 NP 完全之所以能够成立的前提假设; 2.掌握 P 类与 NP 类问题的划分; 3.掌握利用近似算法解决问题的基本思想,能对其可靠性进行分。 (二)教学内容 第一节 问题分类 1. 主要内容 计算模型:确定性图灵机 DTM、非确定性图灵机 NDTM 问题的分类:P 类与 NP 类问题、不可解问题 2. 基本概念和知识点 DTM 与 NDTM P 类与 NP 类问题 此内容的教学过程中,要介绍一下计算机之父 A.M.Turing,及等价于计算机 界的 NOBEL 奖地位的“图灵奖”得主中,于 2000 年获得图灵奖的华人姚期 智教授,计算理论包括伪随机数生成、密码学与通信复杂度的突出贡献,美 国计算机协会(ACM)把 2000 年度的图灵奖授予他。姚期智是图灵奖创立 以来首位获奖的亚裔学者,也是迄今为止获此殊荣的唯一华裔计算机科学家。 姚期智教授放弃了自己在美国优厚的工作待遇,甚至是不惜变卖自己在美国 的房产回国,充分展现了中华学子的爱国情怀!同时强调:姚期智教授在计 算理论中所做出的突出贡献,充实和完善了 NP 完全理论的知识体系。 3. 问题与知识要点 问题及其分类,问题的难度与时间复杂性关系、NP 类问题的证明 第二节 NP 完全问题与 NP-hard 问题 1.主要内容

P完全问题的定义、NP完全问题的证明,C0OK定理 NP完全理论,是计算机科学与技术专业的理论,专业的大厦总是建立在理论成立的 前提下的。从NP完全理论的定义讲解中,让学生明白:任何一个理论,必然基于至少 一个的理论假设:而NP完全理论之所以成立,是在针对P是否等于NP问题这个七大 干禧年难题之 ,假设NP学P的! 通过P完全理论的教学,可使得学生们对《列宁选 集》第2卷第315页所闸述的真理观有一个实际的感悟,即:“绝对真理是由发展中的 相对真理的总和构成:相对真理是不依赖于人类而存在的客体的相对正确的反映:这些 反映日趋正确:每一科学真理尽管有相对性,其中都含有绝对真理的成分。” 2.基本概念和知识点 NPC、COOK定理、常见的NPC问题 3 问题与应用 团问题、VC问题、SAT问题、IS问题的NPC 证明 了解NP完全性问题,掌握P类与NP类问题的划分。 第三节近似算法 1.主要内剂 近似算法的基本思想及性能 基本概念和知识 点 近似算法的基本思想、近似算法的性能评估、分析何类问题须用近似算法求 解。 3.问题与应用 顶点覆盖问题的近似算法,集合覆盖问题的近似算法,HAMILTON问题的近 似算法 掌握利用近似算法解决问题的基本思想,能对其可靠性进行分析。 (三)实践环节与课后练习 VC问题的近似算法及其实现 (四)教学方法与手段 课堂讲授为主,结合课堂分组讨论
8 NP 完全问题的定义、NP 完全问题的证明,COOK 定理 NP 完全理论,是计算机科学与技术专业的理论,专业的大厦总是建立在理论成立的 前提下的。从 NP 完全理论的定义讲解中,让学生明白:任何一个理论,必然基于至少 一个的理论假设:而 NP 完全理论之所以成立,是在针对 P 是否等于 NP 问题这个七大 千禧年难题之一,假设 NP≠P 的! 通过 NP 完全理论的教学,可使得学生们对《列宁选 集》第 2 卷第 315 页所阐述的真理观有一个实际的感悟,即:“绝对真理是由发展中的 相对真理的总和构成;相对真理是不依赖于人类而存在的客体的相对正确的反映;这些 反映日趋正确;每一科学真理尽管有相对性,其中都含有绝对真理的成分。” 2. 基本概念和知识点 NPC、COOK 定理、常见的 NPC 问题 3. 问题与应用 团问题、VC 问题、SAT 问题、IS 问题的 NPC 证明 了解 NP 完全性问题,掌握 P 类与 NP 类问题的划分。 第三节 近似算法 1.主要内容 近似算法的基本思想及性能 2. 基本概念和知识点 近似算法的基本思想、近似算法的性能评估、分析何类问题须用近似算法求 解。 3. 问题与应用 顶点覆盖问题的近似算法,集合覆盖问题的近似算法,HAMILTON 问题的近 似算法。 掌握利用近似算法解决问题的基本思想,能对其可靠性进行分析。 (三)实践环节与课后练习 VC 问题的近似算法及其实现 (四)教学方法与手段 课堂讲授为主,结合课堂分组讨论
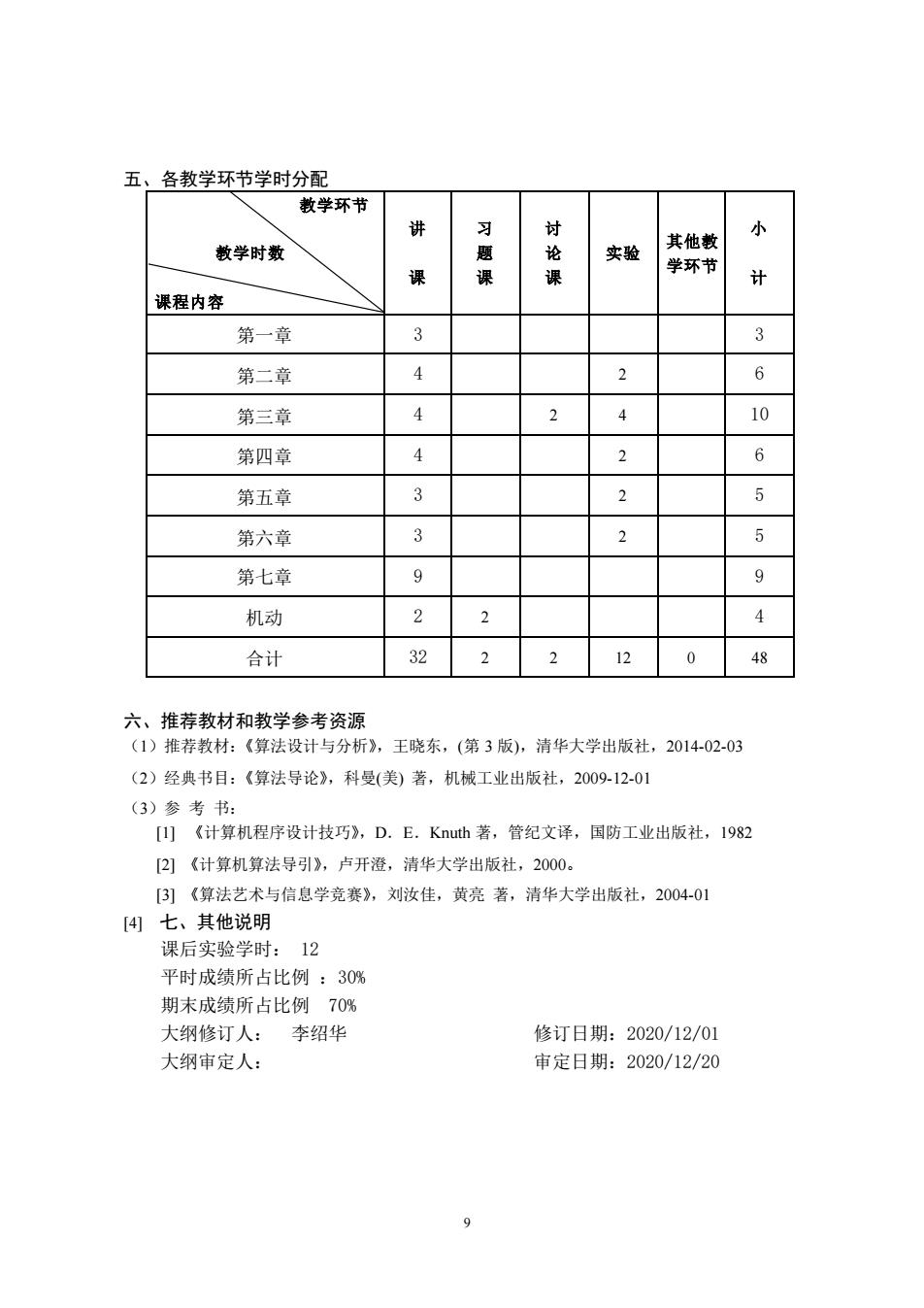
五、各教学环节学时分配 教学环节 习 讨 小 教学时数 实验 其他李 0 学环节 课 女 课程内容 第一章 3 3 第二章 4 6 第三章 10 第四章 2 6 第五章 2 5 第六章 5 第七章 9 机动 2 合计 22 120 六、推荐教材和教学参考资源 (1)推荐教林:《算法设计与分析》,王晓东,(第3版),清华大学出版社,2014-02-03 (2)经典书目:《算法导论》,科曼(美)著,机械工业出版社,200912-01 (3)参考书: [)《计算机程序设计技巧》,D.E.Knuh著,管纪文译,国防工业出版社,1982 [2]《计算机算法导引》,卢开澄,清华大学出版社,2000。 [3)《算法艺术与信息学竞赛》,刘汝佳,黄亮著,清华大学出版社,2004-01 [4七、其他说明 课后实验学时:12 平时成绩所占比例:30% 期末成绩所占比例70% 大纲修订人:李绍华 修订日期:2020/12/01 大纲审定人: 审定日期:2020/12/20
9 五、各教学环节学时分配 教学环节 教学时数 课程内容 讲 课 习 题 课 讨 论 课 实验 其他教 学环节 小 计 第一章 3 3 第二章 4 2 6 第三章 4 2 4 10 第四章 4 2 6 第五章 3 2 5 第六章 3 2 5 第七章 9 9 机动 2 2 4 合计 32 2 2 12 0 48 六、推荐教材和教学参考资源 (1)推荐教材:《算法设计与分析》,王晓东,(第 3 版),清华大学出版社,2014-02-03 (2)经典书目:《算法导论》,科曼(美) 著,机械工业出版社,2009-12-01 (3)参 考 书: [1] 《计算机程序设计技巧》,D.E.Knuth 著,管纪文译,国防工业出版社,1982 [2] 《计算机算法导引》,卢开澄,清华大学出版社,2000。 [3] 《算法艺术与信息学竞赛》,刘汝佳,黄亮 著,清华大学出版社,2004-01 [4] 七、其他说明 课后实验学时: 12 平时成绩所占比例 :30% 期末成绩所占比例 70% 大纲修订人: 李绍华 修订日期:2020/12/01 大纲审定人: 审定日期:2020/12/20