
第三节数理统计基础知识
第三节 数理统计基础知识
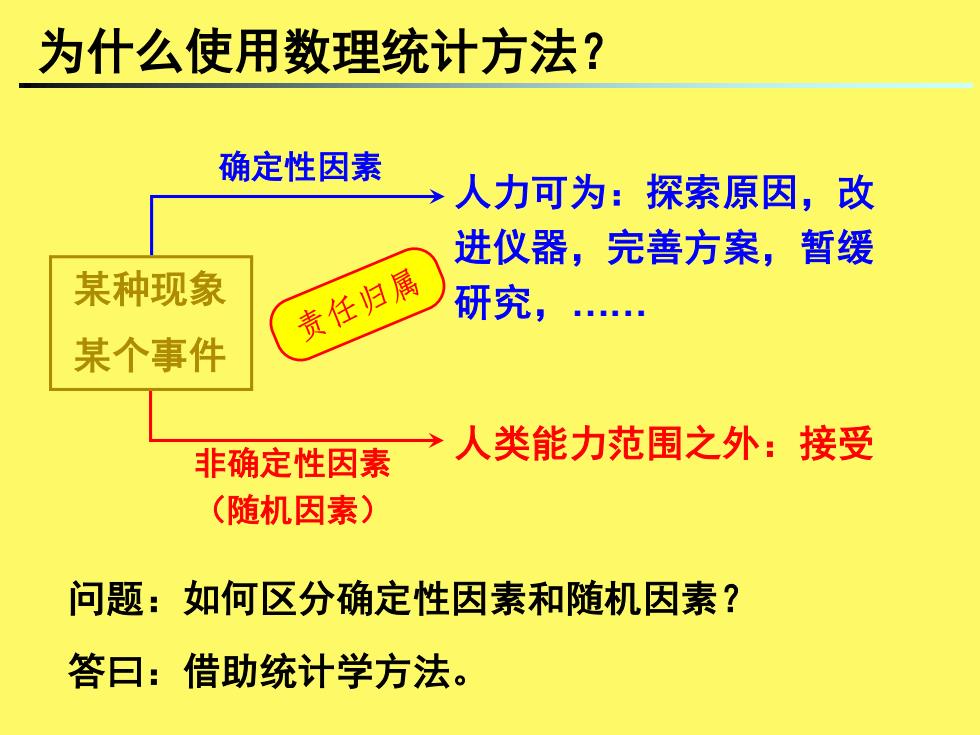
为什么使用数理统计方法? 确定性因素 人力可为:探索原因,改 进仪器,完善方案,暂缓 某种现象 责任归属 研究,. 某个事件 非确定性因素 →人类能力范围之外:接受 (随机因素) 问题:如何区分确定性因素和随机因素? 答曰:借助统计学方法
为什么使用数理统计方法? 人力可为:探索原因,改 进仪器,完善方案,暂缓 研究,. 人类能力范围之外:接受 确定性因素 非确定性因素 (随机因素) 问题:如何区分确定性因素和随机因素? 答曰:借助统计学方法。 某种现象 某个事件

关于概率和数理统计 ◆人类很早就知道随机现象,但是直到近代才发 展出了概率论,并不是缺乏必要的数学工具, 而是概率论所需要的哲学观点。 ◆决定论者否认随机性,认为不确定性仅仅表明 知识缺乏程度,倘若知道的足够多,至少在理 论上可以消除所有的不确定性。 一个特点是相对简单的数学和抽象难懂的概念。 ◆另一个特点是容易实施,难以阐释
关于概率和数理统计 ◆ 一个特点是相对简单的数学和抽象难懂的概念。 ◆ 另一个特点是容易实施,难以阐释。 ◆ 人类很早就知道随机现象,但是直到近代才发 展出了概率论,并不是缺乏必要的数学工具, 而是概率论所需要的哲学观点。 ◆ 决定论者否认随机性,认为不确定性仅仅表明 知识缺乏程度,倘若知道的足够多,至少在理 论上可以消除所有的不确定性

理解随机因素的研究策略 特点由随机因素决定的单次事件的结果不可预知 由确定性因素决定的事件的结果可以预知,因为遵循 特定规律 策略通过统计学方法研究随机因素 理解 统计学方法源于解决实际问题,与人类日常活 动有着密切的联系,是朴素思维活动的系统化 日常生活中,对于只有发生后才能知道确切结 果的事件,如何处理?一经验! 随机因素服从统计规律,即多个实例表现出的规律性
理解随机因素的研究策略 日常生活中,对于只有发生后才能知道确切结 果的事件,如何处理?—— 经验! 策略 通过统计学方法研究随机因素 特点 由随机因素决定的单次事件的结果不可预知 统计学方法源于解决实际问题,与人类日常活 动有着密切的联系,是朴素思维活动的系统化 理解 随机因素服从统计规律,即多个实例表现出的规律性 由确定性因素决定的事件的结果可以预知,因为遵循 特定规律
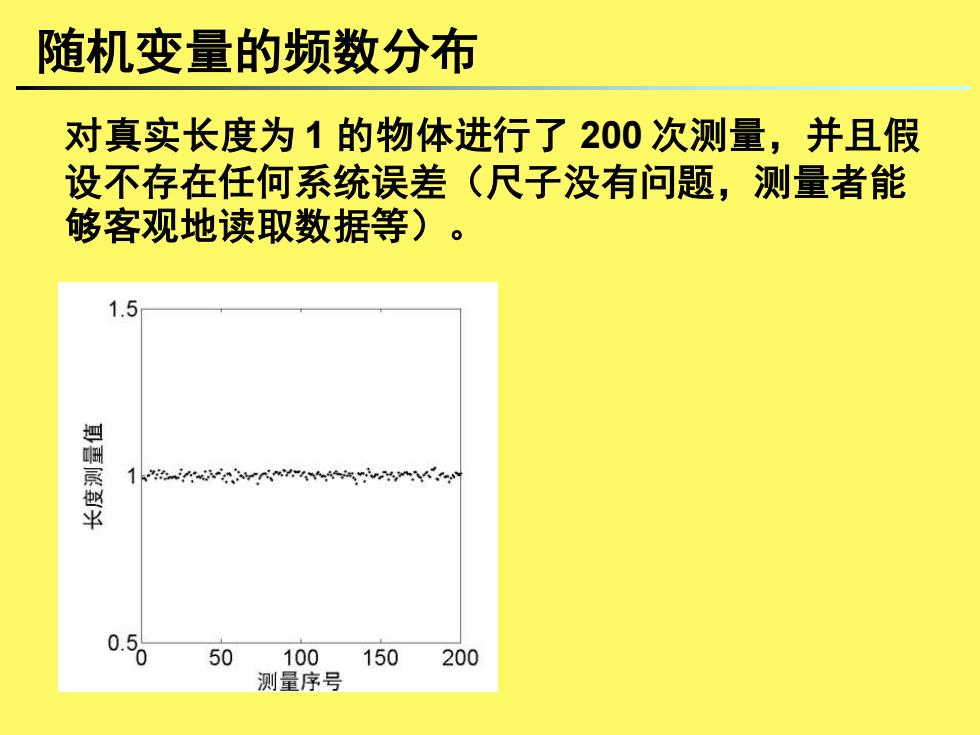
随机变量的频数分布 对真实长度为1的物体进行了200次测量,并且假 设不存在任何系统误差(尺子没有问题,测量者能 够客观地读取数据等)。 1.5 1VKK 寧 0.5 50 100 150 200 测量序号
随机变量的频数分布 对真实长度为 1 的物体进行了 200 次测量,并且假 设不存在任何系统误差(尺子没有问题,测量者能 够客观地读取数据等)

基本概念 随机变量:取值随机、而在确定范围内取值具有确 定概率的变量 随机变量的分布:随机变量的大量取值所表现出的 统计规律性 概率密度函数(PDF):函数化的随机变量分布, 通常以p表示。 累积分布函数(CDF):PDF的积分,通常以P表示 P()=广poa
随机变量:取值随机、而在确定范围内取值具有确 定概率的变量 随机变量的分布:随机变量的大量取值所表现出的 统计规律性 概率密度函数(PDF):函数化的随机变量分布, 通常以 p 表示。 累积分布函数(CDF):PDF的积分,通常以 P 表示 基本概念
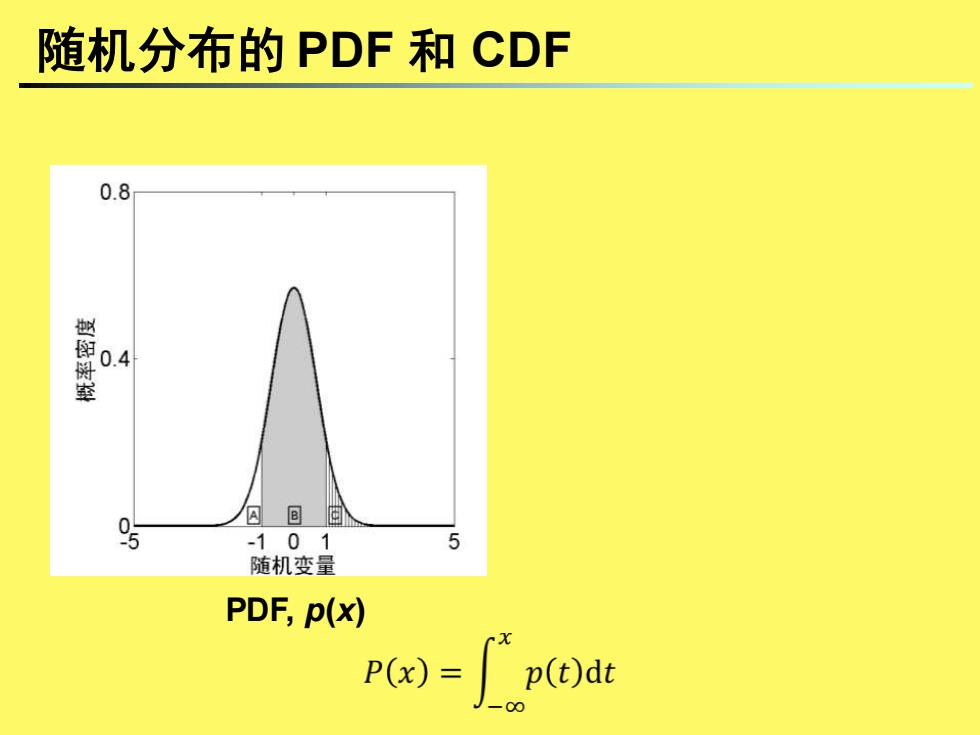
随机分布的PDF和CDF 0.8 0.4 囚回间 -101 5 随机变量 PDF,p(x) P(x)= p()dt
随机分布的 PDF 和 CDF PDF, p(x) CDF, P(x)

正态分布 正态分布(normal distribution),表示为 N(4,o2);概率密度函数(PDF)为高斯函数。 (x-u)2 p(x)= 2G2 0√2元 p一概率密度; x一测量值 一总体平均值;σ一标准偏差
正态分布 正态分布 (normal distribution) ,表示为 N(, 2 );概率密度函数 (PDF) 为高斯函数 。 p — 概率密度; x — 测量值 μ — 总体平均值; σ — 标准偏差

(1)极大值处在x=4,表明大多数测量值在4附 近,即平均值能够较好地反映数据的集中趋势; 1 (2)Pmax= √2元,概率密度的极大值取决于。: (3)以x=”成镜面对称,说明正负误差出现的概 率相等; (4)x→士o0时,y→0,说明极大误差出现的概率 为0。 9
9 (2) ,概率密度的极大值取决于σ; (1)极大值处在 x = μ, 表明大多数测量值在 μ 附 近,即平均值能够较好地反映数据的集中趋势; (3)以 x = μ 成镜面对称,说明正负误差出现的概 率相等; (4) 时,y→0,说明极大误差出现的概率 为0。 x →
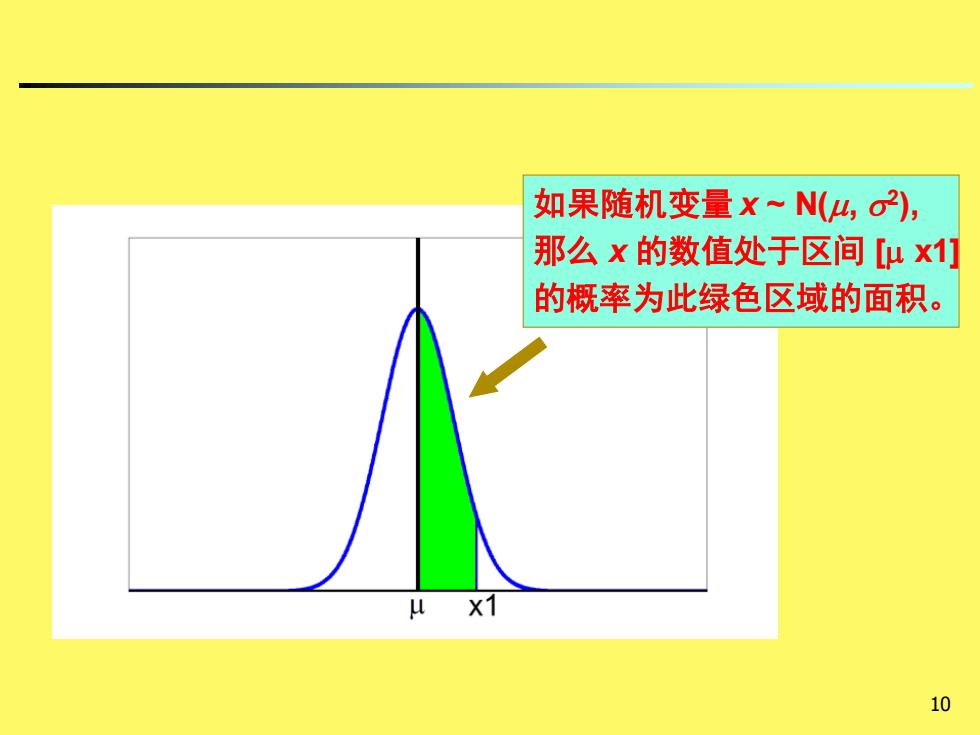
如果随机变量X~N(山,o2), 那么x的数值处于区间[μx1] 的概率为此绿色区域的面积。 10
10 如果随机变量 x ~ N(, 2 ), 那么 x 的数值处于区间 [ x1] 的概率为此绿色区域的面积