第三章 溶液—一多组分体系热力学 1.定义:一种以上的物质,以分子或原子大 小混合,且物理性质和化学组成均 匀一致的体系一一溶液或混合物 2.特性:混合体系是均匀体系 热力学性质是相同或连续的 3.分类:气态溶体一气体混合物 液态混合物一一-山,g-l,s-1构成的液态混合物 固态混合物一s-$,也叫固溶体
1 第三章 溶液——多组分体系热力学 1. 定义:一种以上的物质,以分子或原子大 小混合,且物理性质和化学组成均 匀一致的体系——溶液或混合物 3. 分类:气态溶体——气体混合物 2. 特性:混合体系是均匀体系 热力学性质是相同或连续的 液态混合物——l-l, g-l,s-l 构成的液态混合物 固态混合物——s-s,也叫固溶体

溶液:一种以上,液固均匀体系,多组分不 等同,有溶质溶剂之分,热力学处理 方法不同 混合物:一种以上,g,1,s均匀体系,无溶 质与溶剂之分,热力学处理方法相同 液体混合物一一理想溶液 2
2 溶液:一种以上,液固均匀体系,多组分不 等同,有溶质溶剂之分,热力学处理 方法不同 混合物:一种以上,g,l,s 均匀体系,无溶 质与溶剂之分,热力学处理方法相同 液体混合物——理想溶液

§3.1气体组分的化学势 1.理想气体组分的化学势 1)纯组分理想气体 1molB(P)T→1molB(P) OG )Gm=G8 d业B=dG d Gm=-SmdT+VmdP 等工a=vap fdu=oH.r μgμB°=RTLn-
3 §3.1 气体组分的化学势 1. 理想气体组分的化学势 1)纯组分理想气体 1mol B(P θ ) ⎯T →1mol B(P) μB = T P nB G , ( ) =Gm =GB dμB =d Gm d Gm = - Sm dT+Vm dP 等 T,dμ= Vm dP d = V dP P P m μB -μB θ=RTLn P P

P μB (T,P)=μB°(T)+RTLn o T,P时的化学势表示式 μ(T):标准状态的化学势 2)混合理想气体 理想气体间无相互作用,分子本身大小为质点 体系中每种组分的热力学性质和单独存在时相同 混合态中每种组分的行为与该气体单独存在 时占有同样体积时的行为相同 混合态中某种气体的化学势和在纯态时的相同
4 μθ(T):标准状态的化学势 2)混合理想气体 T,P 时的化学势表示式 理想气体间无相互作用,分子本身大小为质点 体系中每种组分的热力学性质和单独存在时相同 混合态中每种组分的行为与该气体单独存在 时占有同样体积时的行为相同 混合态中某种气体的化学势和在纯态时的相同 μB (T,P)=μB θ (T)+ RTLn P P
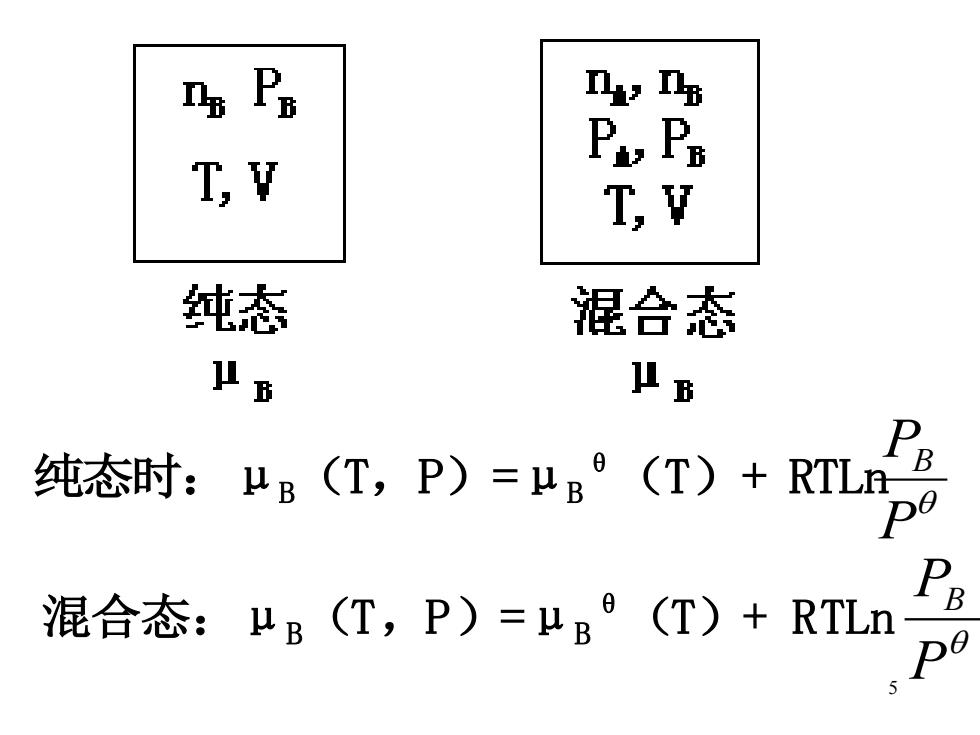
马P n s P& TV T,V 纯态 混合态 八B 八B 纯态时:B(T,P)=B(T)+RTLn 混合态:μB(T,P)=μB(T)+RTLn
5 纯态时:μB (T,P)=μB θ (T)+ RTLn P PB 混合态:μB (T,P)=μB θ (T)+ RTLn P PB

道尔顿分压定律:PPX X:B组分的摩尔分数;P:混合态中的总压 μB(T,P)=μB(T)+RTLn TRTL P + RTLnxB =μ*B(T,P)+RTLnxs μB(T,P)=μB(T,P)+RTLnXB P μ*:(T,P)=μB(T)+RTLn 6
6 xB:B 组分的摩尔分数;P:混合态中的总压 道尔顿分压定律:PB =PxB μB (T,P)=μB θ (T)+ RTLn P PB =μθ B (T)+ RTLn P P + RTLnxB =μ* B(T,P)+ RTLnxB μB(T,P)=μ* B(T,P)+ RTLnxB μ* B (T,P)=μθ B (T)+ RTLn P P

说明:a)μ*(T,P)为等T,P时,x=1, 纯B的化学势,不是标准态(P≠P) b)若P=P°,μ*(T,P)为标准态化学势 2.实际气体的化学势 1)纯实际气体的化学势 等T,实际气体状态变化 dG=VdPdμBdG=VdP 积分:μBu=dP
7 说明:a)μ* B(T,P)为等 T,P 时,xB =1, 纯 B 的化学势,不是标准态(P≠P θ) b)若 P=Pθ,μ* B(T,P θ)为标准态化学势 2. 实际气体的化学势 1)纯实际气体的化学势 等 T,实际气体状态变化 dG=VdP dμB =dG= VdP 积分:μB -μB θ= P P VdP

已知实际气体状态方程V=V(P) 有200多种实际气体状态方程,且较复杂, 不易计算μB 路易斯(Lewis)提出: 若把实际气体与理想气体之间的偏差, 反映在化学势的表示式中,也即在其压力项 上进行修正,而保留了与理想气体化学势公 式相一致的形式,引入逸度f 8
8 已知实际气体状态方程 V=V(P) 路易斯(Lewis)提出: 若把实际气体与理想气体之间的偏差, 反映在化学势的表示式中,也即在其压力项 上进行修正,而保留了与理想气体化学势公 式相一致的形式,引入逸度 f 有 200 多种实际气体状态方程,且较复杂, 不易计算μB

压力为P的理想气体: HB(T,P)=业B°(T)+RTLn P 压力为P的实际气体: BT,P)=B(T)+RTLn f=YP 说明:a)实际气体压力为P的化学势与理想 气体压力为f的化学势相等 PV=nRT fV≠nRT 9
9 压力为 P 的理想气体: μB (T,P)=μB θ (T)+ RTLn P P 压力为 P 的实际气体: μB (T,P)=μB θ (T)+ RTLn P f f=γP 说明:a)实际气体压力为 P 的化学势与理想 气体压力为 f 的化学势相等 PV=nRT fV≠nRT

b)逸度f,逸度系数Y f=YP =1 y=Lim'p P→0Y→1f→P P→0 实际气体就是理想气体 Y为校正因子,无量刚的,它的大小与T, P, 气体的种类有关 反映了实际气体与理想气体的偏差 P较小时,Y〈1 P较大时,Y〉1 P→0时,Y=1 10
10 b)逸度 f,逸度系数γ f=γP 1 0 = = → P f Lim P γ为校正因子,无量刚的,它的大小与 T, P,气体的种类有关 P 较小时,γ 1 P→0 时, γ=1P→0 γ→1 f→P 实际气体就是理想气体 反映了实际气体与理想气体的偏差