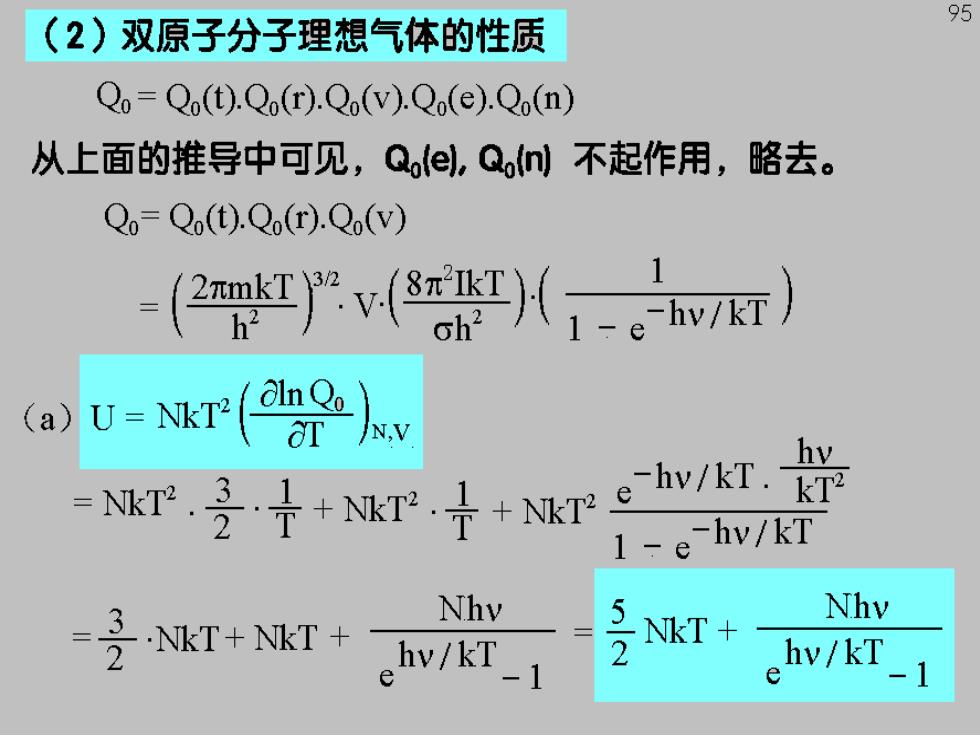
95 (2)双原子分子理想气体的性质 Qo=Q().Q(r).Q().Q(e).Q(n) 从上面的推导中可见,Qoel,Qo们不起作用,略去。 Qo-Qo(t).Qo(r).Qo(V) =(v1-e7a) tN( (a) hv =T,子+NT+mre灯 2 -e-hv/kT 1 Nhy 含k如+T+w成 Nhv 1 号 hv/kT e

当T较低时,化工袋=0,:为00-600K 96 分母值为e“~e”,后项可忽路,U= NkT。 2 当T较高时,贤<1令兴=x,。1+x 则有: Nhv Nhy hv/kT_1 =NkT 1+ hv kT -1 U 子NkT 可知双原子理想气体的摩尔内能低温时为 号R 高温时为子RT

97 (b)Cv-()xw 高温时Cvm子Ngk=子R,低温时Cvm多Ngk=三R 与实验结果相符合。 (3)第一定律的解释(统计解释)》 对于理想气体,是独立子体系 U=∑n81 相依子体系还要增加一项位能) dU=ed血+nde,与dU=δQ-8W,比较, cdh=δQ,n:de=-δW

Σnd:是能级变化对内能的贡献,外界对体系做功, 将使能级发生变化,最明显的是平动能级与 V有关,V变化使c:变化,这时将有功产生。 这一项可以证明如下: 、 gie5kT ,则e=-kT(ln +In Q) Q Ngi (点s-k灯(e :P-(=NT(0e)

99 令R卡=k灯()-(奈e 相当于一个粒子所呈现的压强。 当T,N不变时,d,=-PdV,代入原式, nds;=->n;Pdv=-(n;P dv =PdV =-6W: 各粒子显示的压力之和为P,既然证明了Σndc 代表功,则∑8dn:必定代表热量。 Q,-8edn,-z[-kTh是g+lhQ】dn =-kTg(h是g+-in dn, 做功后使能级发生移动但能级上的粒子数不变, 说明热量是由体系内的粒子在能级上重新分布而 改变的内能的量

99a (4)理想气体反应的平衡常数 a、平衡常数的统计表达式 aA+bB ←51 IL mM 独立子,等同系 A.Gr =-RT In Kp K的#表示热力学平衡常数。 △,G=lGtm+mGm-aGm-bG8m 而且有: G=-NkTn是-Tn是+U

几种物质的平衡常数表达式必须选取一个共同坐标, 即须用Q表示,而我们只知道Q,表示式,所以式中 要出现Uo项。 Gg-k灯hg=-krng+U △,Ga=-RTln ( +AUo.m 其中△,Um=[IU0m(L)+mUgm(M)] -[aUo (A)+bUoem (B)] 是在基态(或0K),(这时各种运动都处于基态)
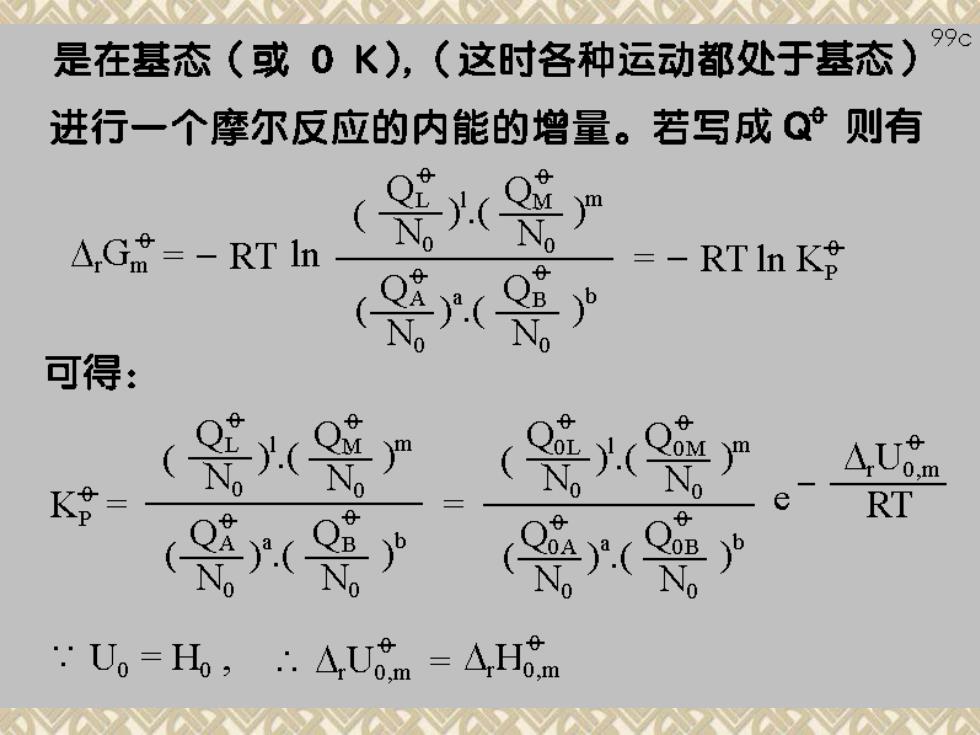
99 是在基态(或0K),(这时各种运动都处于基态) 进行一个摩尔反应的内能的增量。若写成Q则有 △,Gt=-RTln =-RT In K8 ( 可得: AUo.m KB= e RT Uo=Ho,.A,Uom =A,Ho.m

99d 将Q,变换一下,可得平衡常数的统计表达式的 另一种形式: Qooi=Qo(t).Qo(r).Qo(v).Q(e).Qo(n)=Q(t).Qo(i) =Q(①). 2元mkT32 No kT =f.No' kT 则有 =f.k 代入Kg表达式: K9= A.Uo.m f.f (。 RT

99e 有时用单位体积内的分子数来表达平衡常数更方便。 PV -1 kT,→义号为单位体积内的分子数。 KN (是冷 导州 式中△v= (+m)-(a+b)