
3.化学变化的△G 1)定义式:△G=△IHm-T△Sm 由298K的△H,Sm计算△H,△Sm △G(T)=△H(T)-T△S(T) △H(T)=△H(298K)+.ACpdT 298 A.S (T)AS(29K)C J298T 说明:无论可逆与否,都可由定义式 计算△G
1 3.化学变化的ΔG 1)定义式:Δr Gm =Δ r Hm -TΔ r Sm 由 298K 的Δf Hm,Sm 计算Δr Hm,Δr Sm Δ r G(T)=Δ r H(T)-TΔ r S(T) Δr H(T)=Δr H(298K)+ C dT T P 298 Δr S(T)=Δr S(298K)+ dT T T CP 298 说明:无论可逆与否,都可由定义式 计算Δr G

2)由标准生成吉布斯自由能△G9,计算△G 定义:在标准状态下(T,P),由稳定单质 完全反应生成1mo1标态下的化合物时,反应 的自由能变化值△G9 为该化合物的标准摩尔生成自由能 一般T=298K,△G9m (298K) 换句话:一切隐定单质的△G9,29)=0 2
2 2)由标准生成吉布斯自由能Δf G m ,计算Δr G 定义: 在标准状态下(T,P θ),由稳定单质 完全反应生成 1mol 标态下的化合物时,反应 的自由能变化值 Δf G m ——为该化合物的标准摩尔生成自由能 一般 T=298K,Δf G m (298K) 换句话:一切稳定单质的Δf G m (298K)=0

g+(g) 298K,P9 >NH (g) 2 2 G9 298K)=△fG (可查表) h2 NMH3(298K) △Gg229x)=0,△G229)-0 m 与△H9Ns类似 通式: △G品=(∑y,△,G品)产物(∑y,A,G品:)反物 说明:无需是否可逆 3
3 2 1 N2 (g)+ 2 3 H2 (g)⎯⎯ ⎯→ 298K,P NH3 (g) Δr G m (298K) Δf G m N2(298K)=0,Δf G m H2(298K)=0 通式: Δr G m = ( ) , j m j j j G 产物-( ), i m i i i G 反应物 =Δf G m NH3(298K) (可查表) 与Δf H m NH3类似 说明:无需是否可逆

3)电化学法 把化学反应安排成可逆电池,这时反应是以 可逆方式进行的,随着反应的进行,体系对 外做功W’ 可逆电池一 可逆过程 W=nFE n:1摩尔反应时得失电子量 F:1摩尔电子的电量,96480库仑(96500) E:电池电动势(可测) 等TP,可逆电池:△Gm=-W=-nFE
4 3)电化学法 可逆电池——可逆过程 W`=nFE n:1 摩尔反应时得失电子量 F:1 摩尔电子的电量,96480 库仑(96500) E:电池电动势(可测) 等 TP,可逆电池:Δr Gm=-W`=- nFE 把化学反应安排成可逆电池,这时反应是以 可逆方式进行的,随着反应的进行,体系对 外做功 W’

4)化学反应等温式 △GmF-RTLnKp+RTLnQ (1)Kp,Qp K——平衡常数 任意反应的压力熵 (2)化学反应等温式的推导 通过设计可逆过程,导出化学反应等温式 5
5 4)化学反应等温式 Δ r Gm =-RTLnKP +RTLnQP (1)KP,QP KP——平衡常数 QP——任意反应的压力熵 (2)化学反应等温式的推导 通过设计可逆过程,导出化学反应等温式

aA(P)+dD(P)-P.RgG(P)+hH() T,R△G, T,R△G aAP)+dD()T.P.RAC20→gG(Pe)+hHE〉 △G,F△G1+△G,2+△G3 宽 =aRTLn- +dRTLn PD 6
6 aA(PA )+dD(PD )⎯T ⎯,P, ⎯R,r ⎯Gm2 ⎯=0 →gG(PG )+hH(PH ) aA(P ` A )+dD(P ` D ) ⎯⎯⎯⎯⎯→ 1 T ,P`, IR, r Gm gG(P ` G )+hH(P` H ) T,R ΔG1 T,R ΔG3 Δ r Gm, 1 =ΔG1 +Δ r Gm,2+ΔG3 ΔG1 = V dP A A P P ` A + V dP D D P P ` D = dP P A aRT A P P A ` + dP P D dRT D P P D ` =aRTLn ` A A P P + dRTLn ` D D P P

同理:△G=gRTLn- P。 PH AG,F△G1+△G=-RTLnK+RTLnQ 在意
7 Δ r Gm, 1 =ΔG1 + ΔG3 =-RTLnKP +RTLnQP KP =( ) d D a A h H g G P P P P 平衡 QP =( ) ` ` ` ` d D a A h H g G P P P P 任意 同理:ΔG3 = gRTLn G G P P ' + hRTLn H H P P

(3)范特霍夫平衡箱一可逆过程的设计 等T PA P'c Px 可逆过程T,P,凸,G=0 aA(PA)+dD(Pn)>gG(Pc)+hH(P 8
8 (3)范特霍夫平衡箱——可逆过程的设计 等 T 可逆过程
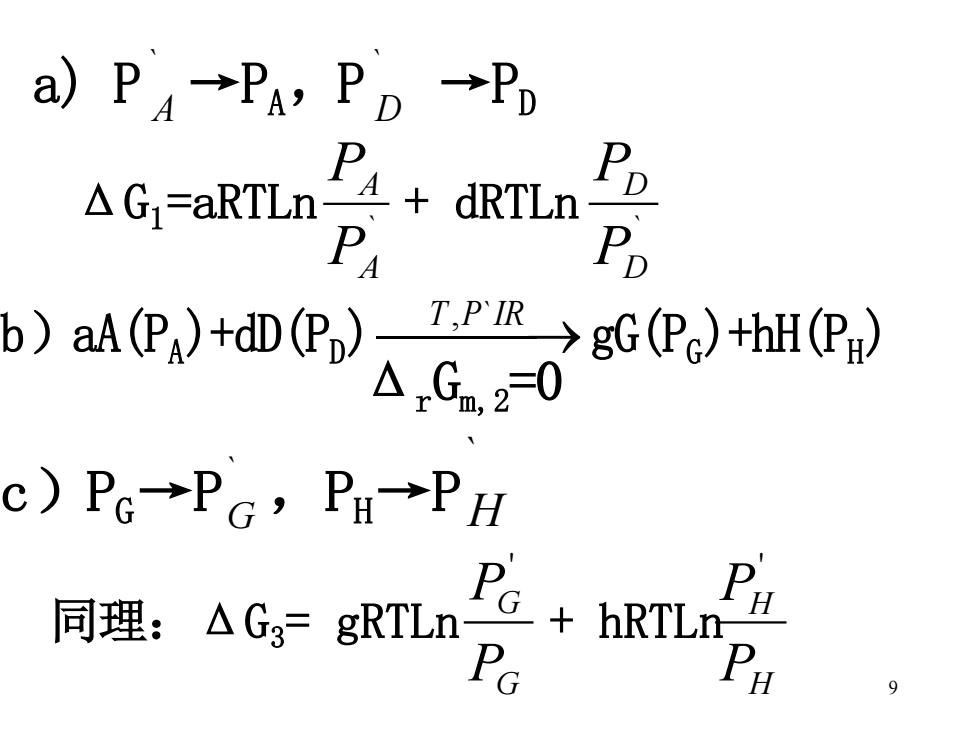
aP4→PA,PD→PD AGFaRTLn4+dRiLn PA D>a4R)DA6司s0r C)Pc→PG,PH→PH 同理:△G3=gRTLn PG PH
9 a) P ` A →PA ,P ` D →PD ΔG1 =aRTLn ` A A P P + dRTLn ` D D P P b)aA(PA )+dD(PD )⎯T ⎯,P ⎯`IR→gG(PG )+hH(PH ) Δ r Gm, 2 =0 c)PG →P ` G ,PH →P ` H 同理:ΔG3 = gRTLn G G P P ' + hRTLn H H P P

△Gn△G1+△G,2+△G3 =-RTLnK +RTLnQp 通过平衡箱,得到可逆平衡反应 平衡箱:宏观上,反应物和产物都不变 若外界干扰,加入反应物,减少产物量,即 物质的量在改变, 但始终保持平衡箱内的反应达到平衡, 即△Gm,20, 而△G.实际上为平衡箱外的反应的△G.的变化 10
10 Δ r Gm =ΔG1 +Δ r Gm,2+ΔG3 =-RTLnKP +RTLnQP 通过平衡箱,得到可逆平衡反应 平衡箱:宏观上,反应物和产物都不变 若外界干扰,加入反应物,减少产物量,即 物质的量在改变, 但始终保持平衡箱内的反应达到平衡, 即Δr Gm,2=0, 而Δr Gm实际上为平衡箱外的反应的Δr Gm的变化