
1 浙江大学 遗传学第五章 1 第五章 数量性状遗传 浙江大学 遗传学第五章 2 1. 数量性状的特征及与质量性状的区别; 2. 遗传率和在育种上的应用; 3. 数量性状的基因定位; 4. 近亲繁殖和回交的遗传效应; 5. 纯系学说和意义; 6. 杂种优势。 本章重点 浙江大学 遗传学第五章 3 前述的遗传现象是基于一个共同的遗传本质,即生物体 的遗传表现直接由其基因型所决定Î可根据遗传群体的表现 变异推测群体的基因型变异或基因的差异。 质量性状(qualitative trait)的特点:表现型和基因型 的变异不连续(discontinuous)。 在杂种后代的分离群体中 Î 可以采用经典遗传学分析方法, 研究其遗传动态。 浙江大学 遗传学第五章 4 生物界中还存在另一类遗传性状,其表现型变异是 连续的(continuous)Î数量性状(quantitative trait)。 例如,人高、动物体重、植株生育期、果实大小, 产量高低等。 表现型变异分析 Î 推断群体的 遗传变异Î借助数量统计的分析方法 Î分析数量性状的遗传规律。 ②.准连续变异(Quasi continuous variation): 如分蘖数(穗数)、 产蛋量、每穗粒数等, 但大测量值时,每个 数值均可能出现,不 出现有小数点数字。 但有的性状即有质量亦有数量性状的特点Î质量-数量 性状。 数量性状的类别: ①.严格的连续变异(Continuous variation) :如人身高; 株高、粒重、产量;棉花纤维长度、细度、强度等; 浙江大学 遗传学第五章 6 第一节 群体的变异
1 浙江大学 遗传学第五章 1 第五章 数量性状遗传 浙江大学 遗传学第五章 2 1. 数量性状的特征及与质量性状的区别; 2. 遗传率和在育种上的应用; 3. 数量性状的基因定位; 4. 近亲繁殖和回交的遗传效应; 5. 纯系学说和意义; 6. 杂种优势。 本章重点 浙江大学 遗传学第五章 3 前述的遗传现象是基于一个共同的遗传本质,即生物体 的遗传表现直接由其基因型所决定Î可根据遗传群体的表现 变异推测群体的基因型变异或基因的差异。 质量性状(qualitative trait)的特点:表现型和基因型 的变异不连续(discontinuous)。 在杂种后代的分离群体中 Î 可以采用经典遗传学分析方法, 研究其遗传动态。 浙江大学 遗传学第五章 4 生物界中还存在另一类遗传性状,其表现型变异是 连续的(continuous)Î数量性状(quantitative trait)。 例如,人高、动物体重、植株生育期、果实大小, 产量高低等。 表现型变异分析 Î 推断群体的 遗传变异Î借助数量统计的分析方法 Î分析数量性状的遗传规律。 ②.准连续变异(Quasi continuous variation): 如分蘖数(穗数)、 产蛋量、每穗粒数等, 但大测量值时,每个 数值均可能出现,不 出现有小数点数字。 但有的性状即有质量亦有数量性状的特点Î质量-数量 性状。 数量性状的类别: ①.严格的连续变异(Continuous variation) :如人身高; 株高、粒重、产量;棉花纤维长度、细度、强度等; 浙江大学 遗传学第五章 6 第一节 群体的变异
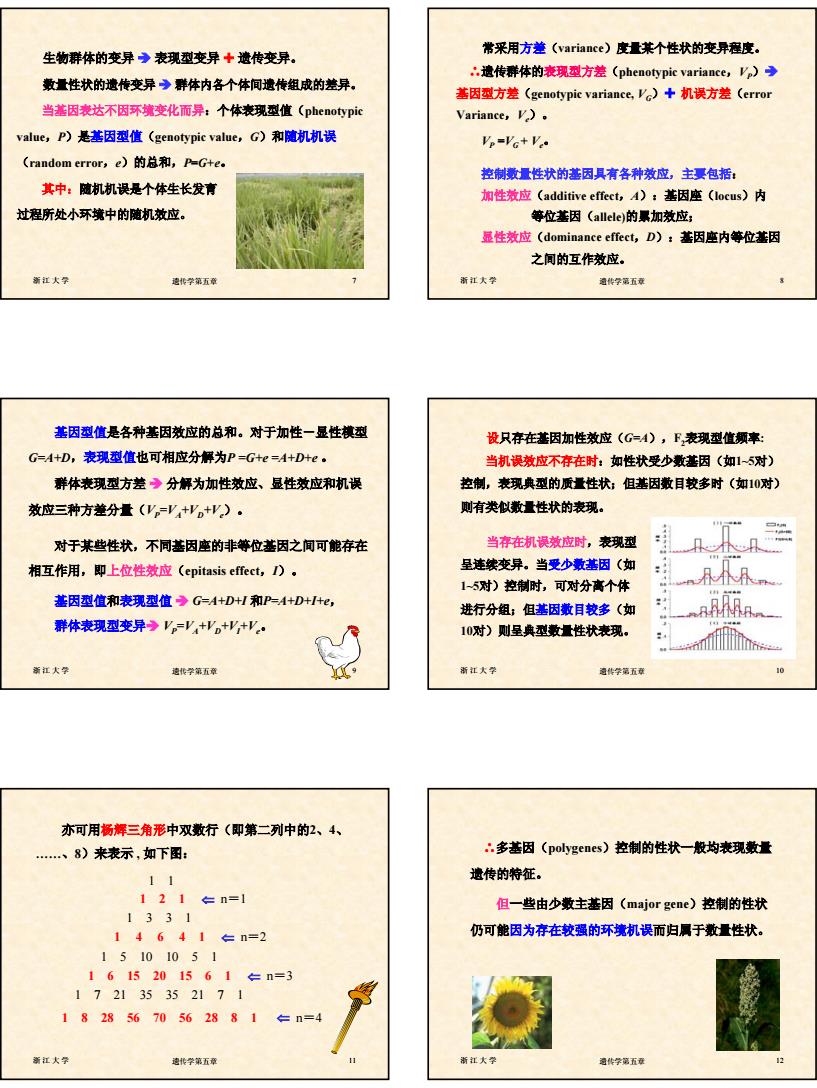
2 浙江大学 遗传学第五章 7 生物群体的变异 Î 表现型变异 ¬ 遗传变异。 数量性状的遗传变异 Î 群体内各个体间遗传组成的差异。 当基因表达不因环境变化而异:个体表现型值(phenotypic value,P)是基因型值(genotypic value,G)和随机机误 (random error,e)的总和,P=G+e。 其中:随机机误是个体生长发育 过程所处小环境中的随机效应。 浙江大学 遗传学第五章 8 常采用方差(variance)度量某个性状的变异程度。 ∴遗传群体的表现型方差(phenotypic variance,VP)Î 基因型方差(genotypic variance, VG)¬ 机误方差(error Variance,Ve)。 VP =VG + Ve。 控制数量性状的基因具有各种效应,主要包括: 加性效应(additive effect,A):基因座(locus)内 等位基因(allele)的累加效应; 显性效应(dominance effect,D):基因座内等位基因 之间的互作效应。 浙江大学 遗传学第五章 9 基因型值是各种基因效应的总和。对于加性-显性模型 G=A+D,表现型值也可相应分解为P =G+e =A+D+e 。 群体表现型方差 Î 分解为加性效应、显性效应和机误 效应三种方差分量(VP=VA+VD+Ve)。 对于某些性状,不同基因座的非等位基因之间可能存在 相互作用,即上位性效应(epitasis effect,I)。 基因型值和表现型值 Î G=A+D+I 和P=A+D+I+e, 群体表现型变异Î VP=VA+VD+VI+Ve。 浙江大学 遗传学第五章 10 设只存在基因加性效应(G=A),F2表现型值频率: 当机误效应不存在时:如性状受少数基因(如1~5对) 控制,表现典型的质量性状;但基因数目较多时(如10对) 则有类似数量性状的表现。 当存在机误效应时,表现型 呈连续变异。当受少数基因(如 1~5对)控制时,可对分离个体 进行分组;但基因数目较多(如 10对)则呈典型数量性状表现。 浙江大学 遗传学第五章 11 亦可用杨辉三角形中双数行(即第二列中的2、4、 .、8)来表示 , 如下图: 1 1 1 2 1 ⇐ n=1 1 3 3 1 1 4 6 4 1 ⇐ n=2 1 5 10 10 5 1 1 6 15 20 15 6 1 ⇐ n=3 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 ⇐ n=4 浙江大学 遗传学第五章 12 ∴多基因(polygenes)控制的性状一般均表现数量 遗传的特征。 但一些由少数主基因(major gene)控制的性状 仍可能因为存在较强的环境机误而归属于数量性状
2 浙江大学 遗传学第五章 7 生物群体的变异 Î 表现型变异 ¬ 遗传变异。 数量性状的遗传变异 Î 群体内各个体间遗传组成的差异。 当基因表达不因环境变化而异:个体表现型值(phenotypic value,P)是基因型值(genotypic value,G)和随机机误 (random error,e)的总和,P=G+e。 其中:随机机误是个体生长发育 过程所处小环境中的随机效应。 浙江大学 遗传学第五章 8 常采用方差(variance)度量某个性状的变异程度。 ∴遗传群体的表现型方差(phenotypic variance,VP)Î 基因型方差(genotypic variance, VG)¬ 机误方差(error Variance,Ve)。 VP =VG + Ve。 控制数量性状的基因具有各种效应,主要包括: 加性效应(additive effect,A):基因座(locus)内 等位基因(allele)的累加效应; 显性效应(dominance effect,D):基因座内等位基因 之间的互作效应。 浙江大学 遗传学第五章 9 基因型值是各种基因效应的总和。对于加性-显性模型 G=A+D,表现型值也可相应分解为P =G+e =A+D+e 。 群体表现型方差 Î 分解为加性效应、显性效应和机误 效应三种方差分量(VP=VA+VD+Ve)。 对于某些性状,不同基因座的非等位基因之间可能存在 相互作用,即上位性效应(epitasis effect,I)。 基因型值和表现型值 Î G=A+D+I 和P=A+D+I+e, 群体表现型变异Î VP=VA+VD+VI+Ve。 浙江大学 遗传学第五章 10 设只存在基因加性效应(G=A),F2表现型值频率: 当机误效应不存在时:如性状受少数基因(如1~5对) 控制,表现典型的质量性状;但基因数目较多时(如10对) 则有类似数量性状的表现。 当存在机误效应时,表现型 呈连续变异。当受少数基因(如 1~5对)控制时,可对分离个体 进行分组;但基因数目较多(如 10对)则呈典型数量性状表现。 浙江大学 遗传学第五章 11 亦可用杨辉三角形中双数行(即第二列中的2、4、 .、8)来表示 , 如下图: 1 1 1 2 1 ⇐ n=1 1 3 3 1 1 4 6 4 1 ⇐ n=2 1 5 10 10 5 1 1 6 15 20 15 6 1 ⇐ n=3 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 ⇐ n=4 浙江大学 遗传学第五章 12 ∴多基因(polygenes)控制的性状一般均表现数量 遗传的特征。 但一些由少数主基因(major gene)控制的性状 仍可能因为存在较强的环境机误而归属于数量性状

3 浙江大学 遗传学第五章 13 生物所处的宏观环境对群体表现具有环境效应(E); 基因在不同环境中表达也可能有所不同,会存在基因型 与环境互作效应(GE)。 ∴生物体在不同环境下的表现型值可细分为: P=E+G+GE+e, 群体表现型变异也可作相应分解: VP= VE+ VG+VGE+Ve。 浙江大学 遗传学第五章 14 ①. 加性-显性遗传体系的互作效应: 加性与环境互作效应(AE) 显性与环境互作效应(DE) ∴个体表现型值:P=E+A+D+AE+DE+e; 表现型方差:VP=VE+VA+VD+VAE+VDE+Ve。 ②. 加性-显性-上位性遗传体系的互作效应: 个体表现型值:P=E+A+D+I+AE+DE+IE+e 表现型方差:VP=VE +VA +VD +VI+VAE+VDE+VIE+Ve。 GE互作效应 浙江大学 遗传学第五章 15 第二节 数量性状的特征 浙江大学 遗传学第五章 16 数量遗传学是在孟德尔经典遗传学的基础上 发展而成的一门学科,但与孟德尔遗传学有明显 的区别。 浙江大学 遗传学第五章 17 1918年费希尔(Fisher R. A. ) 发表 “根据孟德尔遗传假设对亲子间相关性的 研究”论文 Î 统计方法与遗传分析方法 结合 Î 创立数量遗传学。 1925年著《研究工作者统计方法》一书(Statistical Methods for Research Workers),为数量遗传学的研究 提供了有效的分析方法。 首次提出方差分析(ANOVA)方法, 为数量遗传学 发展奠定了基础。 浙江大学 遗传学第五章 18 1.数量性状具有以下特点: ⑴. 数量性状的变异表现为连续性: 杂交后代难以明确分组,只能用度量单位进行测量, 并采用统计学方法加以分析; P1 U P2 Ð F1 表现介于两者之间 Ð F2 连续变异
3 浙江大学 遗传学第五章 13 生物所处的宏观环境对群体表现具有环境效应(E); 基因在不同环境中表达也可能有所不同,会存在基因型 与环境互作效应(GE)。 ∴生物体在不同环境下的表现型值可细分为: P=E+G+GE+e, 群体表现型变异也可作相应分解: VP= VE+ VG+VGE+Ve。 浙江大学 遗传学第五章 14 ①. 加性-显性遗传体系的互作效应: 加性与环境互作效应(AE) 显性与环境互作效应(DE) ∴个体表现型值:P=E+A+D+AE+DE+e; 表现型方差:VP=VE+VA+VD+VAE+VDE+Ve。 ②. 加性-显性-上位性遗传体系的互作效应: 个体表现型值:P=E+A+D+I+AE+DE+IE+e 表现型方差:VP=VE +VA +VD +VI+VAE+VDE+VIE+Ve。 GE互作效应 浙江大学 遗传学第五章 15 第二节 数量性状的特征 浙江大学 遗传学第五章 16 数量遗传学是在孟德尔经典遗传学的基础上 发展而成的一门学科,但与孟德尔遗传学有明显 的区别。 浙江大学 遗传学第五章 17 1918年费希尔(Fisher R. A. ) 发表 “根据孟德尔遗传假设对亲子间相关性的 研究”论文 Î 统计方法与遗传分析方法 结合 Î 创立数量遗传学。 1925年著《研究工作者统计方法》一书(Statistical Methods for Research Workers),为数量遗传学的研究 提供了有效的分析方法。 首次提出方差分析(ANOVA)方法, 为数量遗传学 发展奠定了基础。 浙江大学 遗传学第五章 18 1.数量性状具有以下特点: ⑴. 数量性状的变异表现为连续性: 杂交后代难以明确分组,只能用度量单位进行测量, 并采用统计学方法加以分析; P1 U P2 Ð F1 表现介于两者之间 Ð F2 连续变异
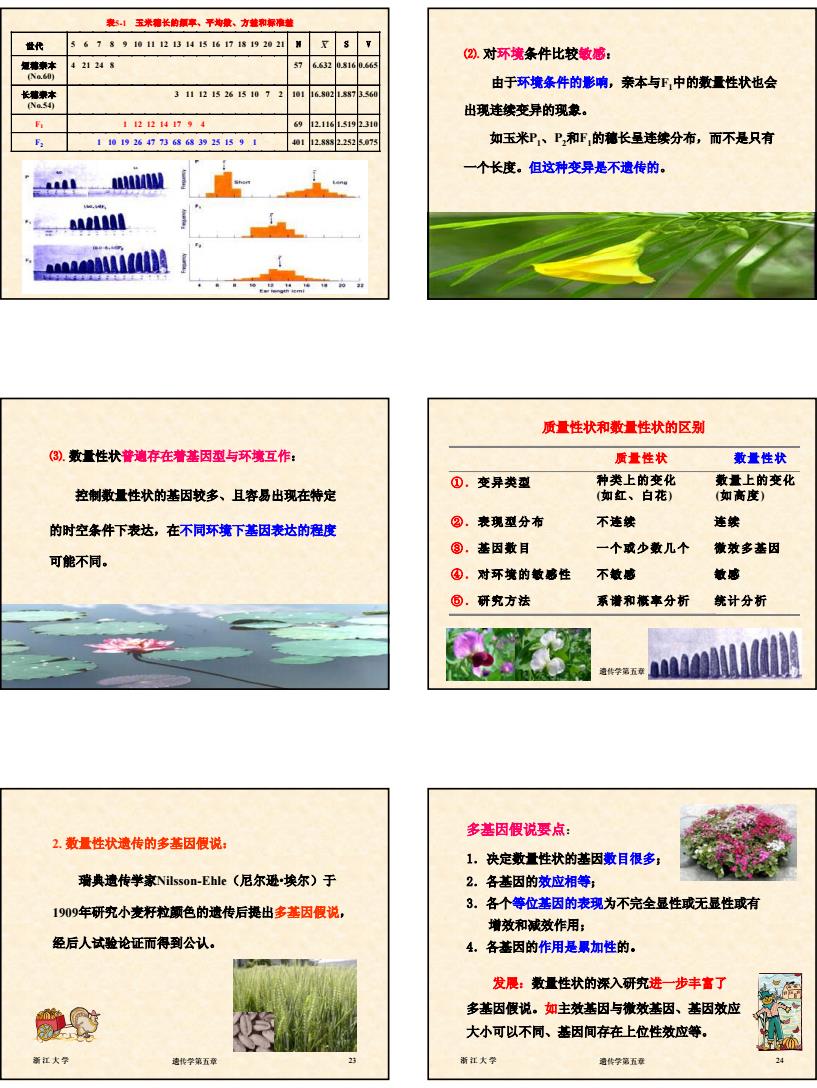
4 浙江大学 遗传学第五章 19 表5-1 玉米穗长的频率、平均数、方差和标准差 世代 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 N X S V 短穗亲本 (No.60) 4 21 24 8 57 6.632 0.816 0.665 长穗亲本 (No.54) 3 11 12 15 26 15 10 7 2 101 16.802 1.887 3.560 F1 1 12 12 14 17 9 4 69 12.116 1.519 2.310 F2 1 10 19 26 47 73 68 68 39 25 15 9 1 401 12.888 2.252 5.075 浙江大学 遗传学第五章 20 ⑵. 对环境条件比较敏感: 由于环境条件的影响,亲本与F1中的数量性状也会 出现连续变异的现象。 如玉米P1、P2和F1的穗长呈连续分布,而不是只有 一个长度。但这种变异是不遗传的。 浙江大学 遗传学第五章 21 ⑶. 数量性状普遍存在着基因型与环境互作: 控制数量性状的基因较多、且容易出现在特定 的时空条件下表达,在不同环境下基因表达的程度 可能不同。 浙江大学 遗传学第五章 22 质量性状和数量性状的区别 质量性状 数量性状 ①.变异类型 种类上的变化 (如红、白花) 数量上的变化 (如高度) ②.表现型分布 不连续 连续 ③.基因数目 一个或少数几个 微效多基因 ④.对环境的敏感性 不敏感 敏感 ⑤.研究方法 系谱和概率分析 统计分析 浙江大学 遗传学第五章 23 2. 数量性状遗传的多基因假说: 瑞典遗传学家Nilsson-Ehle(尼尔逊x埃尔)于 1909年研究小麦籽粒颜色的遗传后提出多基因假说, 经后人试验论证而得到公认。 浙江大学 遗传学第五章 24 多基因假说要点: 1.决定数量性状的基因数目很多; 2.各基因的效应相等; 3.各个等位基因的表现为不完全显性或无显性或有 增效和减效作用; 4.各基因的作用是累加性的。 发展:数量性状的深入研究进一步丰富了 多基因假说。如主效基因与微效基因、基因效应 大小可以不同、基因间存在上位性效应等
4 浙江大学 遗传学第五章 19 表5-1 玉米穗长的频率、平均数、方差和标准差 世代 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 N X S V 短穗亲本 (No.60) 4 21 24 8 57 6.632 0.816 0.665 长穗亲本 (No.54) 3 11 12 15 26 15 10 7 2 101 16.802 1.887 3.560 F1 1 12 12 14 17 9 4 69 12.116 1.519 2.310 F2 1 10 19 26 47 73 68 68 39 25 15 9 1 401 12.888 2.252 5.075 浙江大学 遗传学第五章 20 ⑵. 对环境条件比较敏感: 由于环境条件的影响,亲本与F1中的数量性状也会 出现连续变异的现象。 如玉米P1、P2和F1的穗长呈连续分布,而不是只有 一个长度。但这种变异是不遗传的。 浙江大学 遗传学第五章 21 ⑶. 数量性状普遍存在着基因型与环境互作: 控制数量性状的基因较多、且容易出现在特定 的时空条件下表达,在不同环境下基因表达的程度 可能不同。 浙江大学 遗传学第五章 22 质量性状和数量性状的区别 质量性状 数量性状 ①.变异类型 种类上的变化 (如红、白花) 数量上的变化 (如高度) ②.表现型分布 不连续 连续 ③.基因数目 一个或少数几个 微效多基因 ④.对环境的敏感性 不敏感 敏感 ⑤.研究方法 系谱和概率分析 统计分析 浙江大学 遗传学第五章 23 2. 数量性状遗传的多基因假说: 瑞典遗传学家Nilsson-Ehle(尼尔逊x埃尔)于 1909年研究小麦籽粒颜色的遗传后提出多基因假说, 经后人试验论证而得到公认。 浙江大学 遗传学第五章 24 多基因假说要点: 1.决定数量性状的基因数目很多; 2.各基因的效应相等; 3.各个等位基因的表现为不完全显性或无显性或有 增效和减效作用; 4.各基因的作用是累加性的。 发展:数量性状的深入研究进一步丰富了 多基因假说。如主效基因与微效基因、基因效应 大小可以不同、基因间存在上位性效应等
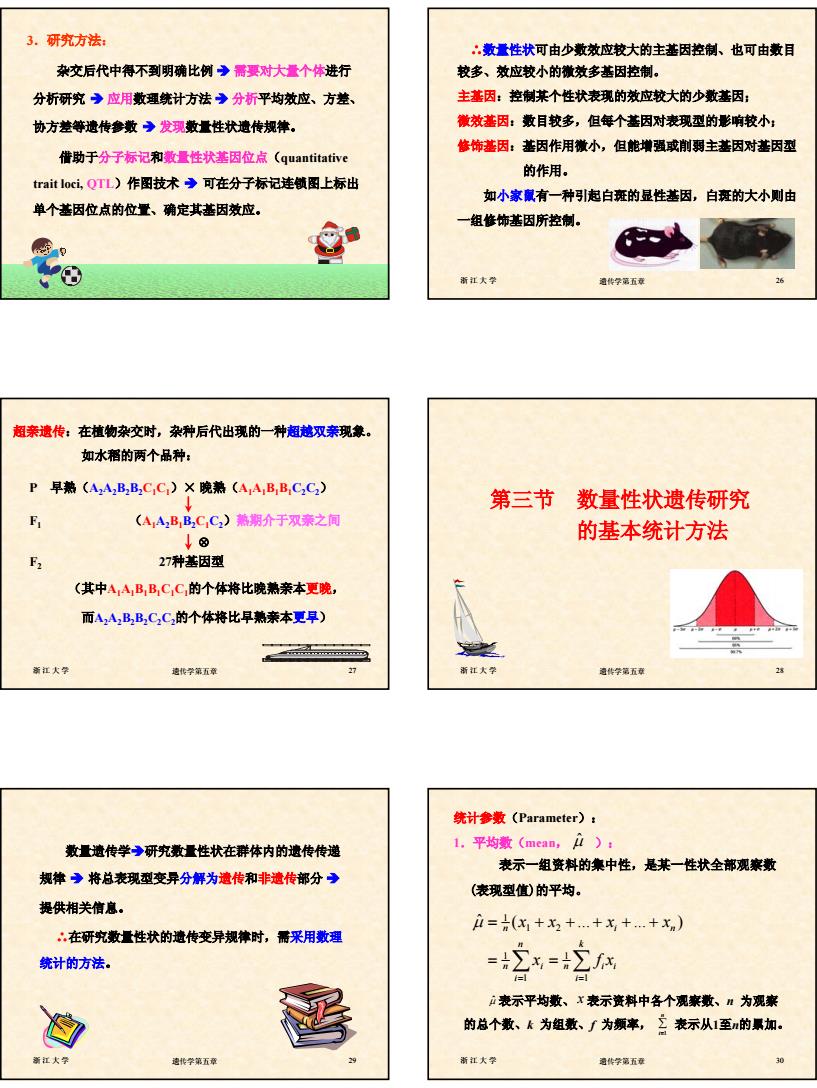
5 浙江大学 遗传学第五章 25 3.研究方法: 杂交后代中得不到明确比例 Î 需要对大量个体进行 分析研究 Î 应用数理统计方法 Î 分析平均效应、方差、 协方差等遗传参数 Î 发现数量性状遗传规律。 借助于分子标记和数量性状基因位点(quantitative trait loci, QTL)作图技术 Î 可在分子标记连锁图上标出 单个基因位点的位置、确定其基因效应。 浙江大学 遗传学第五章 26 ∴数量性状可由少数效应较大的主基因控制、也可由数目 较多、效应较小的微效多基因控制。 主基因:控制某个性状表现的效应较大的少数基因; 微效基因:数目较多,但每个基因对表现型的影响较小; 修饰基因:基因作用微小,但能增强或削弱主基因对基因型 的作用。 如小家鼠有一种引起白斑的显性基因,白斑的大小则由 一组修饰基因所控制。 浙江大学 遗传学第五章 27 超亲遗传:在植物杂交时,杂种后代出现的一种超越双亲现象。 如水稻的两个品种: P 早熟(A2A2B2B2C1C1)× 晚熟(A1A1B1B1C2C2) F1 (A1A2B1B2C1C2)熟期介于双亲之间 ⊗ F2 27种基因型 (其中A1A1B1B1C1C1的个体将比晚熟亲本更晚, 而A2A2B2B2C2C2的个体将比早熟亲本更早) 浙江大学 遗传学第五章 28 第三节 数量性状遗传研究 的基本统计方法 浙江大学 遗传学第五章 29 数量遗传学Î研究数量性状在群体内的遗传传递 规律 Î 将总表现型变异分解为遗传和非遗传部分 Î 提供相关信息。 ∴在研究数量性状的遗传变异规律时,需采用数理 统计的方法。 浙江大学 遗传学第五章 30 表示一组资料的集中性,是某一性状全部观察数 (表现型值)的平均。 1 1 2 1 1 1 1 ˆ ( . . ) n i n n k n n i ii i i xx x x x fx µ = = = + ++++ = = ∑ ∑ µˆ 表示平均数、 x 表示资料中各个观察数、n 为观察 的总个数、k 为组数、f 为频率, ∑ = n i 1 表示从1至n的累加。 统计参数(Parameter): 1.平均数(mean, ): µˆ
5 浙江大学 遗传学第五章 25 3.研究方法: 杂交后代中得不到明确比例 Î 需要对大量个体进行 分析研究 Î 应用数理统计方法 Î 分析平均效应、方差、 协方差等遗传参数 Î 发现数量性状遗传规律。 借助于分子标记和数量性状基因位点(quantitative trait loci, QTL)作图技术 Î 可在分子标记连锁图上标出 单个基因位点的位置、确定其基因效应。 浙江大学 遗传学第五章 26 ∴数量性状可由少数效应较大的主基因控制、也可由数目 较多、效应较小的微效多基因控制。 主基因:控制某个性状表现的效应较大的少数基因; 微效基因:数目较多,但每个基因对表现型的影响较小; 修饰基因:基因作用微小,但能增强或削弱主基因对基因型 的作用。 如小家鼠有一种引起白斑的显性基因,白斑的大小则由 一组修饰基因所控制。 浙江大学 遗传学第五章 27 超亲遗传:在植物杂交时,杂种后代出现的一种超越双亲现象。 如水稻的两个品种: P 早熟(A2A2B2B2C1C1)× 晚熟(A1A1B1B1C2C2) F1 (A1A2B1B2C1C2)熟期介于双亲之间 ⊗ F2 27种基因型 (其中A1A1B1B1C1C1的个体将比晚熟亲本更晚, 而A2A2B2B2C2C2的个体将比早熟亲本更早) 浙江大学 遗传学第五章 28 第三节 数量性状遗传研究 的基本统计方法 浙江大学 遗传学第五章 29 数量遗传学Î研究数量性状在群体内的遗传传递 规律 Î 将总表现型变异分解为遗传和非遗传部分 Î 提供相关信息。 ∴在研究数量性状的遗传变异规律时,需采用数理 统计的方法。 浙江大学 遗传学第五章 30 表示一组资料的集中性,是某一性状全部观察数 (表现型值)的平均。 1 1 2 1 1 1 1 ˆ ( . . ) n i n n k n n i ii i i xx x x x fx µ = = = + ++++ = = ∑ ∑ µˆ 表示平均数、 x 表示资料中各个观察数、n 为观察 的总个数、k 为组数、f 为频率, ∑ = n i 1 表示从1至n的累加。 统计参数(Parameter): 1.平均数(mean, ): µˆ
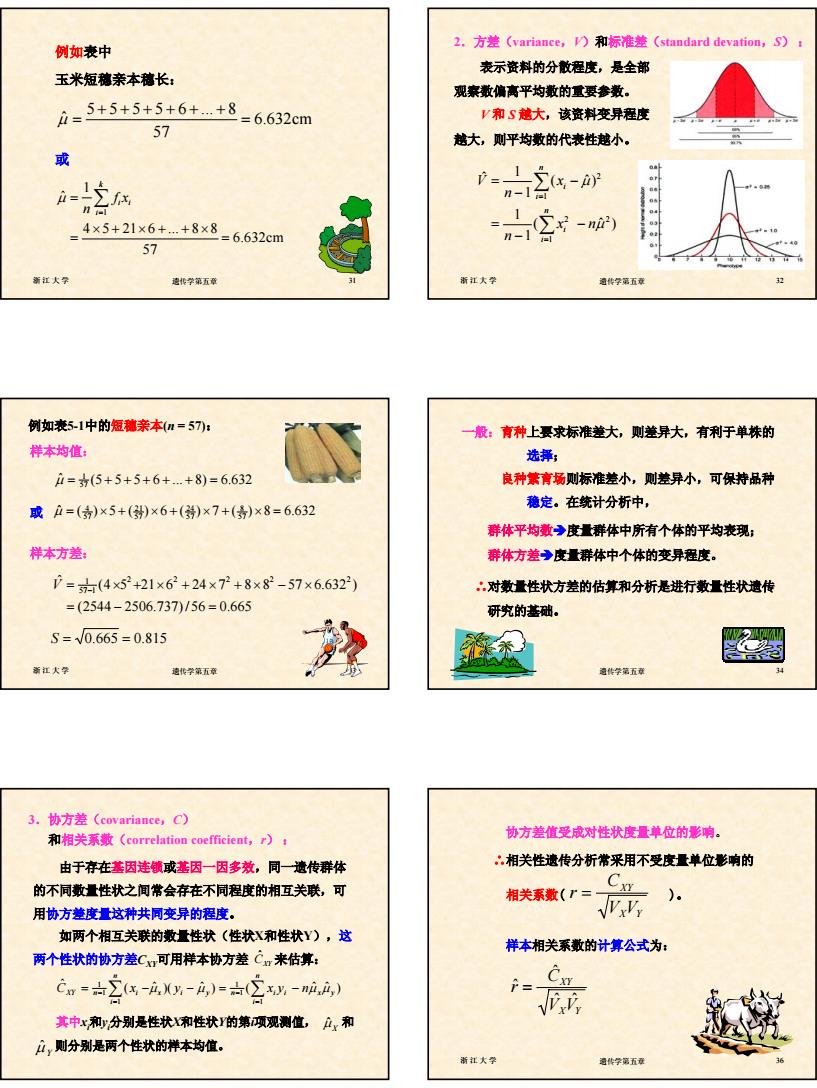
6 浙江大学 遗传学第五章 31 例如表中 玉米短穗亲本穗长: 5 5 5 5 6 . 8 ˆ 6.632cm 57 µ +++++ + = = 或 1 1 ˆ 4 5 21 6 . 8 8 6.632cm 57 k i i i f x n µ = = ×+ ×+ +× = = ∑ 浙江大学 遗传学第五章 32 2.方差(variance,V)和标准差(standard devation,S) : 表示资料的分散程度,是全部 观察数偏离平均数的重要参数。 V 和 S 越大,该资料变异程度 越大,则平均数的代表性越小。 ∑ ∑ = = − − = − − = n i i n i i x n n x n V 1 2 2 1 2 ( ˆ ) 1 1 ( ˆ) 1 1 ˆ µ µ 浙江大学 遗传学第五章 33 例如表5-1中的短穗亲本(n = 57): 样本均值: 1 57 µˆ = ++++ + = (5 5 5 6 . 8) 6.632 ˆ ( ) 5 ( ) 6 ( ) 7 ( ) 8 6.632 57 8 57 24 57 21 57 4 或 µ = × + × + × + × = 样本方差: (2544 2506.737)/ 56 0.665 (4 5 21 6 24 7 8 8 57 6.632 ) ˆ 2 2 2 2 2 57 1 1 = − = V = − × + × + × + × − × S = 0.665 = 0.815 浙江大学 遗传学第五章 34 一般:育种上要求标准差大,则差异大,有利于单株的 选择; 良种繁育场则标准差小,则差异小,可保持品种 稳定。在统计分析中, 群体平均数Î度量群体中所有个体的平均表现; 群体方差Î度量群体中个体的变异程度。 ∴对数量性状方差的估算和分析是进行数量性状遗传 研究的基础。 其中xi 和yi 分别是性状X和性状Y的第i项观测值, 和 则分别是两个性状的样本均值。 由于存在基因连锁或基因一因多效,同一遗传群体 的不同数量性状之间常会存在不同程度的相互关联,可 用协方差度量这种共同变异的程度。 如两个相互关联的数量性状(性状X和性状Y),这 两个性状的协方差CXY可用样本协方差 来估算: CXY ˆ ( ˆ )( ˆ ) ( ˆ ˆ ) ˆ 1 1 1 1 1 1 x y n i x i y n i i n i CXY = n ∑ xi −µ y − µ = ∑x y − nµ µ = − = − µ Xˆ µ Y ˆ 3.协方差(covariance,C) 和相关系数(correlation coefficient,r) : 浙江大学 遗传学第五章 36 协方差值受成对性状度量单位的影响。 ∴相关性遗传分析常采用不受度量单位影响的 相关系数( )。 样本相关系数的计算公式为: X Y XY V V C r = X Y XY V V C r ˆ ˆ ˆ ˆ =
6 浙江大学 遗传学第五章 31 例如表中 玉米短穗亲本穗长: 5 5 5 5 6 . 8 ˆ 6.632cm 57 µ +++++ + = = 或 1 1 ˆ 4 5 21 6 . 8 8 6.632cm 57 k i i i f x n µ = = ×+ ×+ +× = = ∑ 浙江大学 遗传学第五章 32 2.方差(variance,V)和标准差(standard devation,S) : 表示资料的分散程度,是全部 观察数偏离平均数的重要参数。 V 和 S 越大,该资料变异程度 越大,则平均数的代表性越小。 ∑ ∑ = = − − = − − = n i i n i i x n n x n V 1 2 2 1 2 ( ˆ ) 1 1 ( ˆ) 1 1 ˆ µ µ 浙江大学 遗传学第五章 33 例如表5-1中的短穗亲本(n = 57): 样本均值: 1 57 µˆ = ++++ + = (5 5 5 6 . 8) 6.632 ˆ ( ) 5 ( ) 6 ( ) 7 ( ) 8 6.632 57 8 57 24 57 21 57 4 或 µ = × + × + × + × = 样本方差: (2544 2506.737)/ 56 0.665 (4 5 21 6 24 7 8 8 57 6.632 ) ˆ 2 2 2 2 2 57 1 1 = − = V = − × + × + × + × − × S = 0.665 = 0.815 浙江大学 遗传学第五章 34 一般:育种上要求标准差大,则差异大,有利于单株的 选择; 良种繁育场则标准差小,则差异小,可保持品种 稳定。在统计分析中, 群体平均数Î度量群体中所有个体的平均表现; 群体方差Î度量群体中个体的变异程度。 ∴对数量性状方差的估算和分析是进行数量性状遗传 研究的基础。 其中xi 和yi 分别是性状X和性状Y的第i项观测值, 和 则分别是两个性状的样本均值。 由于存在基因连锁或基因一因多效,同一遗传群体 的不同数量性状之间常会存在不同程度的相互关联,可 用协方差度量这种共同变异的程度。 如两个相互关联的数量性状(性状X和性状Y),这 两个性状的协方差CXY可用样本协方差 来估算: CXY ˆ ( ˆ )( ˆ ) ( ˆ ˆ ) ˆ 1 1 1 1 1 1 x y n i x i y n i i n i CXY = n ∑ xi −µ y − µ = ∑x y − nµ µ = − = − µ Xˆ µ Y ˆ 3.协方差(covariance,C) 和相关系数(correlation coefficient,r) : 浙江大学 遗传学第五章 36 协方差值受成对性状度量单位的影响。 ∴相关性遗传分析常采用不受度量单位影响的 相关系数( )。 样本相关系数的计算公式为: X Y XY V V C r = X Y XY V V C r ˆ ˆ ˆ ˆ =
7 浙江大学 遗传学第五章 37 第四节 遗传参数的估算 及其应用 浙江大学 遗传学第五章 38 数量遗传学运用统计分析方法 Î 研究性状: 表 现 型 变 异 遗传效应 环境效应 基因主效应变异分量 基因型×环境互作变异分量 浙江大学 遗传学第五章 39 早期研究群体,一般采用遗传差异较大的二个亲本 杂交 Î 分析亲本、F1、F2或回交世代的表现型方差 Î 估算群体的遗传方差或加性、显性等方差分量。 基因型不分离的纯系亲本和F1的变异Î归因于环境 机误变异(Ve),基因型方差等于0。 F2变异 Î 包括分离个体的基因型变异和环境机误 变异( )。 ∴可以估算基因型方差( )。 VF =VG +Ve 2 VG =VF −Ve 2 一、遗传效应及其方差和协方差分析: 浙江大学 遗传学第五章 40 对于动物和异花授粉植物,由于可能存在严重的自交 衰退现象,常用F1表现型方差估算环境机误方差: 。 对于自花授粉植物,也可以用纯系亲本(或自交系) 表现型方差估计环境机误方差: ; 或利用亲本和F1的表现型方差: 。 1 Ve =VF ( ) 2 1 2 1 Ve = VP +VP ( ) 3 1 2 1 1 Ve = VP +VP +VF 浙江大学 遗传学第五章 41 0.665 ˆ 1 VP = ˆ 3.560 2 VP = ˆ 2.310 1 VF = ˆ 5.075 2 VF = 2.310 Vˆ e = ˆ ˆ ˆ 5.075 2.310 2.765 2 VG = VF −Ve = − = 遗传实验观察的个体数有限Î 所得各项方差分量 属于样本方差Î群体方差的估计值。 现以表5-1中玉米穗长试验的结果为例,计算各个 世代的表现型方差分量: 浙江大学 遗传学第五章 42 再增加两个回交世代( 和 ) Î 可进一步估算加性方差和显性方差: VF =VG +Ve =VA +VD +Ve 2 B1 = F1 × P1 B2 = F1 × P2 2 ( ) A F2 B1 B2 V = V − V +V VD = VB +VB −VF −Ve 1 2 2 ( ) 基因型方差(VG)的分解: 如假设不存在基因型与环境的互作效应(VGE=0)和 基因的上位性效应(VI=0),F2表现型方差可以分解为:
7 浙江大学 遗传学第五章 37 第四节 遗传参数的估算 及其应用 浙江大学 遗传学第五章 38 数量遗传学运用统计分析方法 Î 研究性状: 表 现 型 变 异 遗传效应 环境效应 基因主效应变异分量 基因型×环境互作变异分量 浙江大学 遗传学第五章 39 早期研究群体,一般采用遗传差异较大的二个亲本 杂交 Î 分析亲本、F1、F2或回交世代的表现型方差 Î 估算群体的遗传方差或加性、显性等方差分量。 基因型不分离的纯系亲本和F1的变异Î归因于环境 机误变异(Ve),基因型方差等于0。 F2变异 Î 包括分离个体的基因型变异和环境机误 变异( )。 ∴可以估算基因型方差( )。 VF =VG +Ve 2 VG =VF −Ve 2 一、遗传效应及其方差和协方差分析: 浙江大学 遗传学第五章 40 对于动物和异花授粉植物,由于可能存在严重的自交 衰退现象,常用F1表现型方差估算环境机误方差: 。 对于自花授粉植物,也可以用纯系亲本(或自交系) 表现型方差估计环境机误方差: ; 或利用亲本和F1的表现型方差: 。 1 Ve =VF ( ) 2 1 2 1 Ve = VP +VP ( ) 3 1 2 1 1 Ve = VP +VP +VF 浙江大学 遗传学第五章 41 0.665 ˆ 1 VP = ˆ 3.560 2 VP = ˆ 2.310 1 VF = ˆ 5.075 2 VF = 2.310 Vˆ e = ˆ ˆ ˆ 5.075 2.310 2.765 2 VG = VF −Ve = − = 遗传实验观察的个体数有限Î 所得各项方差分量 属于样本方差Î群体方差的估计值。 现以表5-1中玉米穗长试验的结果为例,计算各个 世代的表现型方差分量: 浙江大学 遗传学第五章 42 再增加两个回交世代( 和 ) Î 可进一步估算加性方差和显性方差: VF =VG +Ve =VA +VD +Ve 2 B1 = F1 × P1 B2 = F1 × P2 2 ( ) A F2 B1 B2 V = V − V +V VD = VB +VB −VF −Ve 1 2 2 ( ) 基因型方差(VG)的分解: 如假设不存在基因型与环境的互作效应(VGE=0)和 基因的上位性效应(VI=0),F2表现型方差可以分解为:
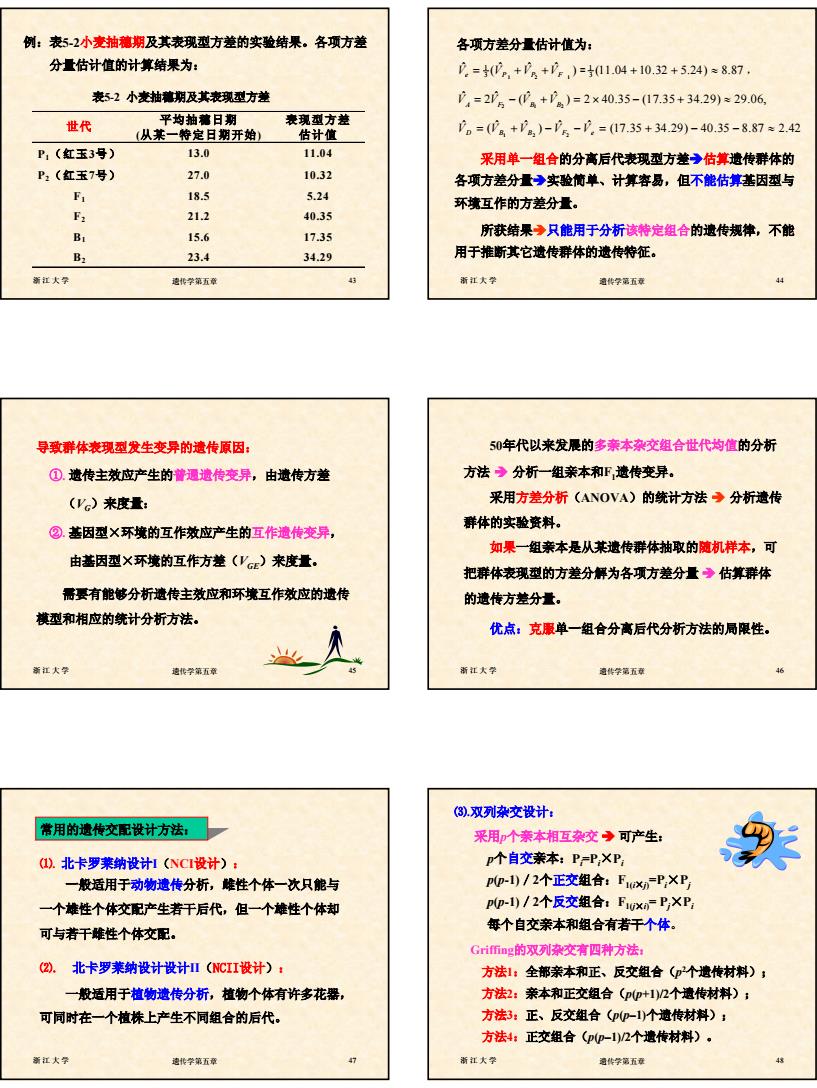
8 浙江大学 遗传学第五章 43 世代 平均抽穗日期 (从某一特定日期开始) 表现型方差 估计值 P1(红玉3号) 13.0 11.04 P2(红玉7号) 27.0 10.32 F1 18.5 5.24 F2 21.2 40.35 B1 15.6 17.35 B2 23.4 34.29 表5-2 小麦抽穗期及其表现型方差 例:表5-2小麦抽穗期及其表现型方差的实验结果。各项方差 分量估计值的计算结果为: 浙江大学 遗传学第五章 44 各项方差分量估计值为: Ve VP VP VF ˆ ˆ ˆ ( ˆ 3 1 2 1 = + + ) 1 = (11.04 10.32 5.24) 8.87 3 1 + + ≈ , 2 12 ˆ ˆ ˆˆ 2 ( ) 2 40.35 (17.35 34.29) 29.06, V V VV A F BB = − + =× − + ≈ (17.35 34.29) 40.35 8.87 2.42 ˆ ˆ ) ˆ ˆ ( ˆ 1 2 2 VD = VB + VB −VF − Ve = + − − ≈ 采用单一组合的分离后代表现型方差Î估算遗传群体的 各项方差分量Î实验简单、计算容易,但不能估算基因型与 环境互作的方差分量。 所获结果Î只能用于分析该特定组合的遗传规律,不能 用于推断其它遗传群体的遗传特征。 浙江大学 遗传学第五章 45 导致群体表现型发生变异的遗传原因: ①. 遗传主效应产生的普通遗传变异,由遗传方差 (VG)来度量: ②. 基因型×环境的互作效应产生的互作遗传变异, 由基因型×环境的互作方差(VGE)来度量。 需要有能够分析遗传主效应和环境互作效应的遗传 模型和相应的统计分析方法。 浙江大学 遗传学第五章 46 50年代以来发展的多亲本杂交组合世代均值的分析 方法 Î 分析一组亲本和F1遗传变异。 采用方差分析(ANOVA)的统计方法 Î 分析遗传 群体的实验资料。 如果一组亲本是从某遗传群体抽取的随机样本,可 把群体表现型的方差分解为各项方差分量 Î 估算群体 的遗传方差分量。 优点:克服单一组合分离后代分析方法的局限性。 浙江大学 遗传学第五章 47 ⑴. 北卡罗莱纳设计I(NCI设计): 一般适用于动物遗传分析,雌性个体一次只能与 一个雄性个体交配产生若干后代,但一个雄性个体却 可与若干雌性个体交配。 常用的遗传交配设计方法: ⑵. 北卡罗莱纳设计设计II(NCII设计): 一般适用于植物遗传分析,植物个体有许多花器, 可同时在一个植株上产生不同组合的后代。 浙江大学 遗传学第五章 48 ⑶.双列杂交设计: 采用p个亲本相互杂交 Î 可产生: p个自交亲本:Pi =Pi ×Pi p(p-1)/2个正交组合:F1(i×j) =Pi ×Pj p(p-1)/2个反交组合:F1(j×i) = Pj ×Pi 每个自交亲本和组合有若干个体。 Griffing的双列杂交有四种方法: 方法1:全部亲本和正、反交组合(p2个遗传材料); 方法2:亲本和正交组合(p(p+1)/2个遗传材料); 方法3:正、反交组合(p(p–1)个遗传材料); 方法4:正交组合(p(p–1)/2个遗传材料)
8 浙江大学 遗传学第五章 43 世代 平均抽穗日期 (从某一特定日期开始) 表现型方差 估计值 P1(红玉3号) 13.0 11.04 P2(红玉7号) 27.0 10.32 F1 18.5 5.24 F2 21.2 40.35 B1 15.6 17.35 B2 23.4 34.29 表5-2 小麦抽穗期及其表现型方差 例:表5-2小麦抽穗期及其表现型方差的实验结果。各项方差 分量估计值的计算结果为: 浙江大学 遗传学第五章 44 各项方差分量估计值为: Ve VP VP VF ˆ ˆ ˆ ( ˆ 3 1 2 1 = + + ) 1 = (11.04 10.32 5.24) 8.87 3 1 + + ≈ , 2 12 ˆ ˆ ˆˆ 2 ( ) 2 40.35 (17.35 34.29) 29.06, V V VV A F BB = − + =× − + ≈ (17.35 34.29) 40.35 8.87 2.42 ˆ ˆ ) ˆ ˆ ( ˆ 1 2 2 VD = VB + VB −VF − Ve = + − − ≈ 采用单一组合的分离后代表现型方差Î估算遗传群体的 各项方差分量Î实验简单、计算容易,但不能估算基因型与 环境互作的方差分量。 所获结果Î只能用于分析该特定组合的遗传规律,不能 用于推断其它遗传群体的遗传特征。 浙江大学 遗传学第五章 45 导致群体表现型发生变异的遗传原因: ①. 遗传主效应产生的普通遗传变异,由遗传方差 (VG)来度量: ②. 基因型×环境的互作效应产生的互作遗传变异, 由基因型×环境的互作方差(VGE)来度量。 需要有能够分析遗传主效应和环境互作效应的遗传 模型和相应的统计分析方法。 浙江大学 遗传学第五章 46 50年代以来发展的多亲本杂交组合世代均值的分析 方法 Î 分析一组亲本和F1遗传变异。 采用方差分析(ANOVA)的统计方法 Î 分析遗传 群体的实验资料。 如果一组亲本是从某遗传群体抽取的随机样本,可 把群体表现型的方差分解为各项方差分量 Î 估算群体 的遗传方差分量。 优点:克服单一组合分离后代分析方法的局限性。 浙江大学 遗传学第五章 47 ⑴. 北卡罗莱纳设计I(NCI设计): 一般适用于动物遗传分析,雌性个体一次只能与 一个雄性个体交配产生若干后代,但一个雄性个体却 可与若干雌性个体交配。 常用的遗传交配设计方法: ⑵. 北卡罗莱纳设计设计II(NCII设计): 一般适用于植物遗传分析,植物个体有许多花器, 可同时在一个植株上产生不同组合的后代。 浙江大学 遗传学第五章 48 ⑶.双列杂交设计: 采用p个亲本相互杂交 Î 可产生: p个自交亲本:Pi =Pi ×Pi p(p-1)/2个正交组合:F1(i×j) =Pi ×Pj p(p-1)/2个反交组合:F1(j×i) = Pj ×Pi 每个自交亲本和组合有若干个体。 Griffing的双列杂交有四种方法: 方法1:全部亲本和正、反交组合(p2个遗传材料); 方法2:亲本和正交组合(p(p+1)/2个遗传材料); 方法3:正、反交组合(p(p–1)个遗传材料); 方法4:正交组合(p(p–1)/2个遗传材料)
9 浙江大学 遗传学第五章 49 ⑷.混合线性模型分析方法 : 70年代以来发展的混合线性模型分析方法(mixed linear model approach)Î 可无偏分析ANOVA方法所 不能分析的各种非平衡资料和复杂的遗传模型。 基于Cockerham广义遗传模型建模原理和混合线性 模型的统计分析方法,数量遗传研究已有一些更为复杂 的遗传模型。 浙江大学 遗传学第五章 50 ①. 加性-显性-性连锁-母体效应遗传模型(AD+L+M模型) 哺乳动物或家禽类动物的数量性状¨受常染色体所载的 基因控制¨还可能受母体基因(母体细胞质基因及核基因) 控制;另外动物雌雄体数量性状表现差异也较大¨表明存在 性染色体连锁的基因效应。 采用AD+L+M模型分析一组 亲本和F1组合雌雄个体在多环境 下的实验资料 ¨ 可以无偏估算 表现型方差分量。 浙江大学 遗传学第五章 51 VP =VE +VA +VD +VL +VM +VAE +VDE +VLE +VME +Ve 其中VL是性连锁效应(L)的方差分量,VM是母体效应 (M)的方差分量,VLE是性连锁×环境互作效应方差分量, VME是母体×环境互作效应方差分量。 不同性状表现型协方差分量估算: AE DE LE ME e P E A D L M C C C C C C C C C C C + + + + + = + + + + 浙江大学 遗传学第五章 52 ②. 加性-显性-上位性遗传模型(AD+AA模型) VP =VE +VA +VD +VAA +VAE +VDE +VAAE +Ve 不同性状表现型协方差分量的估算: CP = CE +CA +CD +CAA +CAE +CDE +CAAE +Ce 非等位基因间互作的上位性效应是控制数量性状表现 的重要遗传分量。 采用AD+AA模型分析一组亲本、F1和F2组合在多环境 下的资料 ¨ 可以无偏估算以下表现型方差的各项分量。 其中VAA是加性×加性的上位性效应(AA)方差分量, VAAE是AA上位性×环境互作效应方差分量。 浙江大学 遗传学第五章 53 ③. 种子(或幼畜)遗传模型(AD+C+AmDm模型): 作物种子品质性状和动物幼畜经济性状等复杂 数量性状 ¨ 受种子(或幼畜)核基因、母体细胞质 基因和母体核基因三套遗传体系的控制。 浙江大学 遗传学第五章 54 AE DE CE AmE DmE e P E A D C Am Dm C C C C C C C C C C C C C + + + + + + = + + + + + 不同性状表现型协方差分量的估算: AE DE CE AmE DmE e P E A D C Am Dm V V V V V V V V V V V V V + + + + + + = + + + + + 采用三套遗传体系的 AD+C+AmDm模型分析一组亲本 及F1和F2组合在多环境下的实验资料 ¨ 估算表现型方差的 各项分量:
9 浙江大学 遗传学第五章 49 ⑷.混合线性模型分析方法 : 70年代以来发展的混合线性模型分析方法(mixed linear model approach)Î 可无偏分析ANOVA方法所 不能分析的各种非平衡资料和复杂的遗传模型。 基于Cockerham广义遗传模型建模原理和混合线性 模型的统计分析方法,数量遗传研究已有一些更为复杂 的遗传模型。 浙江大学 遗传学第五章 50 ①. 加性-显性-性连锁-母体效应遗传模型(AD+L+M模型) 哺乳动物或家禽类动物的数量性状¨受常染色体所载的 基因控制¨还可能受母体基因(母体细胞质基因及核基因) 控制;另外动物雌雄体数量性状表现差异也较大¨表明存在 性染色体连锁的基因效应。 采用AD+L+M模型分析一组 亲本和F1组合雌雄个体在多环境 下的实验资料 ¨ 可以无偏估算 表现型方差分量。 浙江大学 遗传学第五章 51 VP =VE +VA +VD +VL +VM +VAE +VDE +VLE +VME +Ve 其中VL是性连锁效应(L)的方差分量,VM是母体效应 (M)的方差分量,VLE是性连锁×环境互作效应方差分量, VME是母体×环境互作效应方差分量。 不同性状表现型协方差分量估算: AE DE LE ME e P E A D L M C C C C C C C C C C C + + + + + = + + + + 浙江大学 遗传学第五章 52 ②. 加性-显性-上位性遗传模型(AD+AA模型) VP =VE +VA +VD +VAA +VAE +VDE +VAAE +Ve 不同性状表现型协方差分量的估算: CP = CE +CA +CD +CAA +CAE +CDE +CAAE +Ce 非等位基因间互作的上位性效应是控制数量性状表现 的重要遗传分量。 采用AD+AA模型分析一组亲本、F1和F2组合在多环境 下的资料 ¨ 可以无偏估算以下表现型方差的各项分量。 其中VAA是加性×加性的上位性效应(AA)方差分量, VAAE是AA上位性×环境互作效应方差分量。 浙江大学 遗传学第五章 53 ③. 种子(或幼畜)遗传模型(AD+C+AmDm模型): 作物种子品质性状和动物幼畜经济性状等复杂 数量性状 ¨ 受种子(或幼畜)核基因、母体细胞质 基因和母体核基因三套遗传体系的控制。 浙江大学 遗传学第五章 54 AE DE CE AmE DmE e P E A D C Am Dm C C C C C C C C C C C C C + + + + + + = + + + + + 不同性状表现型协方差分量的估算: AE DE CE AmE DmE e P E A D C Am Dm V V V V V V V V V V V V V + + + + + + = + + + + + 采用三套遗传体系的 AD+C+AmDm模型分析一组亲本 及F1和F2组合在多环境下的实验资料 ¨ 估算表现型方差的 各项分量:

10 浙江大学 遗传学第五章 55 ♥ 遗传率或遗传力:指遗传方差(VG)在总方差(VP)中 所占比值¨可作为杂种后代进行选择的指标。 遗传率是度量性状的遗传变异占表现型变异相对比率的 重要遗传参数¨是指性状从上一代传递到下一代 的能力。 ♣ 遗传率大,早期选择效果好,如株高、抽穗期等性状; ♣ 遗传率小,早期选择效果差,如穗数、产量等。 二、遗传率的估算和应用: 浙江大学 遗传学第五章 56 2 G GE A D AE DE P P VV VVV V H V V + ++ + = = 简单的数量遗传分析一般假设只包括加性效应(A) 和显性效应(D): 表现型方差简单地分解为: 1. 广义遗传率(heritability in the broadsense,简称H2): 指总的遗传方差占表现型方差的比率: VVV V P = G GE e + + 浙江大学 遗传学第五章 57 2. 狭义遗传率(heritability in the narrow sense,简称h2): 指加性遗传方差占表现型方差的比率: 根据不同的遗传模型可以进一步分解广义遗传率(H2) 和狭义遗传率(h2)¨ 获得不同的遗传率分量。 2 G GE A AE P P VV VV h V V + + = = 浙江大学 遗传学第五章 58 遗传率与育种选择的关系: 根据性状遗传率的大小,容易从表现型鉴别不同的 基因型¨较快地选育出优良的新的类型。 狭义遗传率较高的性状,在杂种早期世代进行选择 ¨ 收效比较明显:而狭义遗传率较低的性状,则在杂种 后期世代 进行选择。 浙江大学 遗传学第五章 59 第五节 数量性状基因定位 浙江大学 遗传学第五章 60 经典数量遗传分析方法Î分析控制数量性状表现 的总遗传效应Î但无法鉴别基因的数目、单个基因在 基因组的位置和遗传效应。 现代分子生物学分子标记技术 Î构建各种作物 的分子标记连锁图谱。 分子标记连锁图谱 数量性状基因位点(quantitative trait loci,简称QTL)定位分析方法 Î估算数量性状 基因位点数目、位置和遗传效应。 常用QTL定位(QTL mapping)方法如下:
10 浙江大学 遗传学第五章 55 ♥ 遗传率或遗传力:指遗传方差(VG)在总方差(VP)中 所占比值¨可作为杂种后代进行选择的指标。 遗传率是度量性状的遗传变异占表现型变异相对比率的 重要遗传参数¨是指性状从上一代传递到下一代 的能力。 ♣ 遗传率大,早期选择效果好,如株高、抽穗期等性状; ♣ 遗传率小,早期选择效果差,如穗数、产量等。 二、遗传率的估算和应用: 浙江大学 遗传学第五章 56 2 G GE A D AE DE P P VV VVV V H V V + ++ + = = 简单的数量遗传分析一般假设只包括加性效应(A) 和显性效应(D): 表现型方差简单地分解为: 1. 广义遗传率(heritability in the broadsense,简称H2): 指总的遗传方差占表现型方差的比率: VVV V P = G GE e + + 浙江大学 遗传学第五章 57 2. 狭义遗传率(heritability in the narrow sense,简称h2): 指加性遗传方差占表现型方差的比率: 根据不同的遗传模型可以进一步分解广义遗传率(H2) 和狭义遗传率(h2)¨ 获得不同的遗传率分量。 2 G GE A AE P P VV VV h V V + + = = 浙江大学 遗传学第五章 58 遗传率与育种选择的关系: 根据性状遗传率的大小,容易从表现型鉴别不同的 基因型¨较快地选育出优良的新的类型。 狭义遗传率较高的性状,在杂种早期世代进行选择 ¨ 收效比较明显:而狭义遗传率较低的性状,则在杂种 后期世代 进行选择。 浙江大学 遗传学第五章 59 第五节 数量性状基因定位 浙江大学 遗传学第五章 60 经典数量遗传分析方法Î分析控制数量性状表现 的总遗传效应Î但无法鉴别基因的数目、单个基因在 基因组的位置和遗传效应。 现代分子生物学分子标记技术 Î构建各种作物 的分子标记连锁图谱。 分子标记连锁图谱 数量性状基因位点(quantitative trait loci,简称QTL)定位分析方法 Î估算数量性状 基因位点数目、位置和遗传效应。 常用QTL定位(QTL mapping)方法如下: