1 浙江大学 遗传学第十四章 1 第十四章 群体遗传与进化 浙江大学 遗传学第十四章 2 1.遗传平衡定律:哈德-魏伯格定律、基因型频率 和基因频率的概念、基因频率计算方法。 2.改变基因频率的因素:突变、选择、遗传漂变和 迁移。 3.生物进化的特点。 4.物种形成的方式、隔离在物种形成过程中的作用。 本章重点 浙江大学 遗传学第十四章 3 遗传学 Î 研究生物遗传和变异的规律和机理; 进化论 Î 研究生物物种的起源和演变过程。 每个物种具有相当稳定的遗传特性,而新种形成 和发展则有赖于可遗传的变异。 ∴ 群体遗传学是研究进化论的必要基础。 群体遗传学的研究: ①. 为生物进化的研究提供更多的证据; ②. 解释生物进化根本原因和历史过程。 浙江大学 遗传学第十四章 4 第一节 群体的遗传平衡 浙江大学 遗传学第十四章 5 个体间互配可使孟德尔遗传因子代代相传Î 遗传学上 称为“孟德尔群体”或“基因库”。 同一群体内个体基因组合虽有不同,但群体中所有的 基因是一定的 Î 基因库指一个群体中所含的基因总数。 有机体繁殖过程 Î 并不能把各个体的基因型传递给 子代,传递给子代的只是不同频率的基因。 遗传学群体的概念:是研究一个群体内基因传递情况及其 频率改变的科学。 群体 是各个体间能互配 (相互交配关系) 的集合体。 浙江大学 遗传学第十四章 6 一、等位基因频率和基因型频率
1 浙江大学 遗传学第十四章 1 第十四章 群体遗传与进化 浙江大学 遗传学第十四章 2 1.遗传平衡定律:哈德-魏伯格定律、基因型频率 和基因频率的概念、基因频率计算方法。 2.改变基因频率的因素:突变、选择、遗传漂变和 迁移。 3.生物进化的特点。 4.物种形成的方式、隔离在物种形成过程中的作用。 本章重点 浙江大学 遗传学第十四章 3 遗传学 Î 研究生物遗传和变异的规律和机理; 进化论 Î 研究生物物种的起源和演变过程。 每个物种具有相当稳定的遗传特性,而新种形成 和发展则有赖于可遗传的变异。 ∴ 群体遗传学是研究进化论的必要基础。 群体遗传学的研究: ①. 为生物进化的研究提供更多的证据; ②. 解释生物进化根本原因和历史过程。 浙江大学 遗传学第十四章 4 第一节 群体的遗传平衡 浙江大学 遗传学第十四章 5 个体间互配可使孟德尔遗传因子代代相传Î 遗传学上 称为“孟德尔群体”或“基因库”。 同一群体内个体基因组合虽有不同,但群体中所有的 基因是一定的 Î 基因库指一个群体中所含的基因总数。 有机体繁殖过程 Î 并不能把各个体的基因型传递给 子代,传递给子代的只是不同频率的基因。 遗传学群体的概念:是研究一个群体内基因传递情况及其 频率改变的科学。 群体 是各个体间能互配 (相互交配关系) 的集合体。 浙江大学 遗传学第十四章 6 一、等位基因频率和基因型频率
2 浙江大学 遗传学第十四章 7 1.基因型和表现型的概念 : 孟德尔的杂交试验之后 Î 遗传学中 提出了基因型和表现型的概念。 基因型是基因的一种组合 Î 个体遗传组成。 表现型指生物个体所表现的性状 Î 基因型与环境 影响共同作用的结果。 浙江大学 遗传学第十四章 8 ①.基因型频率 (genotype frequency): 一个群体内某种特定基因型所占的比例。 ∵一个群体内由许多不同基因型的个体所组合。 基因型是受精时由父母本基因组成Î基因型频率 需从F2的表现型比例推算出来,再从F3加以验证。 2.基因型频率和基因频率: 浙江大学 遗传学第十四章 9 一个群体内特定基因座某一等位基因占该基因座等位基因 总数的比例。基因型频率Î推算出基因频率。 等位基因频率Î决定群体基因性质的基本因素; 环境条件或遗传结构不变Î等位基因频率不会改变。 例: A1A1×A2A2 ↓ F1 A1A2 ↓ F2 1 A1A1 : 2 A1A2 : 1 A2A2 P→F1→F2基因型频率改变,但基因在各代中是复制自己, 代代相传而不改变Î孟德尔群体的基本特征。 ②.基因频率(gene frequency)或 等位基因频率(allele frequency): 浙江大学 遗传学第十四章 10 ♣ 设一对同源染色体某一基因座有一对等位基因A1A2 。 其中A1频率为p、 A2频率为q, 则 p ¬ q = 1 由这一对基因可以构成三种不同基因型 A1A1 A1A2 A2A2 个体数为 N11 N12 N22 ♣ 设群体总个体数为N,即 N11 + N12 + N22 = N 3.基因频率的推算: 浙江大学 遗传学第十四章 11 ∵ 二倍体生物各基因型由两个等位基因组成 Î 如A1A1、A1A2、 A2A2,其中:A1基因有2N11+N12,A2基因有N12+2N22。 ∴ 3种基因型的频率见下表: 基因型频率的计算公式 群体 样本群体 基因型 计数 基因型频率 计数 基因型频率估计 频率估计标准差 A1A1 N11 P11=N11 / N n11 P n / n ˆ 11 = 11 ) ˆ (1 ˆ 11 11 11 1 S P P n = − A1A2 N12 P12=N12 / N n12 P n / n ˆ 12 = 12 ) ˆ (1 ˆ 12 12 12 1 S P P n = − A2A2 N22 P22=N22 / N n22 P n / n ˆ 22 = 22 ) ˆ (1 ˆ 22 22 22 1 S P P n = − 合计 N 1 n 1 浙江大学 遗传学第十四章 12 ∴ 2种等位基因的频率为: 等位基因频率的计算公式 群体 样本群体 基因型 计数 等位基因频率 计数 等位基因频率估计 等位基因频率估计标准差 A1 N1 11 12 11 12 1 2 1 2 2 P P N N N p = + + = n1 11 12 1 11 12 2 ˆ 2 1 ˆ ˆ 2 n n p n P P + = = + 2 ˆ ) ˆ ( ˆ 2 1 1 11 1 2 1 S p P p n = + − A2 N2 22 12 22 12 2 2 1 2 2 P P N N N p = + + = n2 22 12 2 22 12 2 ˆ 2 1 ˆ ˆ 2 n n p n P P + = = + 2 ˆ ) ˆ ( ˆ 2 2 2 22 2 2 1 S p P p n = + − 合计 2N 1 2n 1
2 浙江大学 遗传学第十四章 7 1.基因型和表现型的概念 : 孟德尔的杂交试验之后 Î 遗传学中 提出了基因型和表现型的概念。 基因型是基因的一种组合 Î 个体遗传组成。 表现型指生物个体所表现的性状 Î 基因型与环境 影响共同作用的结果。 浙江大学 遗传学第十四章 8 ①.基因型频率 (genotype frequency): 一个群体内某种特定基因型所占的比例。 ∵一个群体内由许多不同基因型的个体所组合。 基因型是受精时由父母本基因组成Î基因型频率 需从F2的表现型比例推算出来,再从F3加以验证。 2.基因型频率和基因频率: 浙江大学 遗传学第十四章 9 一个群体内特定基因座某一等位基因占该基因座等位基因 总数的比例。基因型频率Î推算出基因频率。 等位基因频率Î决定群体基因性质的基本因素; 环境条件或遗传结构不变Î等位基因频率不会改变。 例: A1A1×A2A2 ↓ F1 A1A2 ↓ F2 1 A1A1 : 2 A1A2 : 1 A2A2 P→F1→F2基因型频率改变,但基因在各代中是复制自己, 代代相传而不改变Î孟德尔群体的基本特征。 ②.基因频率(gene frequency)或 等位基因频率(allele frequency): 浙江大学 遗传学第十四章 10 ♣ 设一对同源染色体某一基因座有一对等位基因A1A2 。 其中A1频率为p、 A2频率为q, 则 p ¬ q = 1 由这一对基因可以构成三种不同基因型 A1A1 A1A2 A2A2 个体数为 N11 N12 N22 ♣ 设群体总个体数为N,即 N11 + N12 + N22 = N 3.基因频率的推算: 浙江大学 遗传学第十四章 11 ∵ 二倍体生物各基因型由两个等位基因组成 Î 如A1A1、A1A2、 A2A2,其中:A1基因有2N11+N12,A2基因有N12+2N22。 ∴ 3种基因型的频率见下表: 基因型频率的计算公式 群体 样本群体 基因型 计数 基因型频率 计数 基因型频率估计 频率估计标准差 A1A1 N11 P11=N11 / N n11 P n / n ˆ 11 = 11 ) ˆ (1 ˆ 11 11 11 1 S P P n = − A1A2 N12 P12=N12 / N n12 P n / n ˆ 12 = 12 ) ˆ (1 ˆ 12 12 12 1 S P P n = − A2A2 N22 P22=N22 / N n22 P n / n ˆ 22 = 22 ) ˆ (1 ˆ 22 22 22 1 S P P n = − 合计 N 1 n 1 浙江大学 遗传学第十四章 12 ∴ 2种等位基因的频率为: 等位基因频率的计算公式 群体 样本群体 基因型 计数 等位基因频率 计数 等位基因频率估计 等位基因频率估计标准差 A1 N1 11 12 11 12 1 2 1 2 2 P P N N N p = + + = n1 11 12 1 11 12 2 ˆ 2 1 ˆ ˆ 2 n n p n P P + = = + 2 ˆ ) ˆ ( ˆ 2 1 1 11 1 2 1 S p P p n = + − A2 N2 22 12 22 12 2 2 1 2 2 P P N N N p = + + = n2 22 12 2 22 12 2 ˆ 2 1 ˆ ˆ 2 n n p n P P + = = + 2 ˆ ) ˆ ( ˆ 2 2 2 22 2 2 1 S p P p n = + − 合计 2N 1 2n 1
3 浙江大学 遗传学第十四章 13 一般难以分析整个群体的所有个体 Î 就难以得到群体 基因型频率(P11、P12、P22)和等位基因频率(p1、p2)。 在群体中抽取一些个体 Î 样本群体 Î 计算基因型数 (n11、n12、n22)和等位基因数(n1、n2)Î 估算群体的 基因型频率( 、 、 )、等位基因频率( 、 )和 相应的标准差。 基因型频率或等位基因频率估计值的标准差 Î 度量 参数的抽样变异。 11 Pˆ 12 Pˆ 22 Pˆ 1 pˆ 2 pˆ 人类第3条染色体有一个细胞表层蛋白基因CCR5,该 基因座的编码区段有一个突变等位基因△32(缺失32bp)Î 正常型等位基因CCR5ª和突变型等位基因CCR5−△32。 3种基因型对爱滋病毒HIV的感染性不同,ª/ª易感染、 发病快,ª/△32易感染、发病慢,△32/△32不易感染。 下表列出了欧洲4个地区人群中 CCR5基因型观察值和基因型频率、 等位基因频率的估计值及其标准差 (Martinson 等,1997)。 浙江大学 遗传学第十四章 15 ①.ª/ª基因型频率估计和标准差: ˆ = 75 102 = 0.7353 P++ 0.7353 (1 0.7353) 0.0437 102 1 S++ = × × − = ②. ª/△32的基因型频率估计和标准差: 24 102 0.2353 Pˆ +− = = 0.2353 (1 0.2353) 0.0420 102 1 S+− = × × − = 以冰岛人群CCR5基因为例,计算基因型频率和 等位基因频率及其标准差: ③.Δ32/Δ32基因型频率估计和标准差: 0.0294 ˆ ˆ 1 Pˆ −− = − P++ − P+− = 0.0294 1 0.0294 0.0167 102 1 S−− = × ×( − )= ④. CCR5ª等位基因频率估计和标准差: pˆ 2 75 24 / 2 102 0.8529 + =( ) ×+ × = ( ) 1 2 0.8529 0.7353 2 0.8529 0.0256 2 102 S+ = + −× = × ( ) ⑤. CCR5-Δ32等位基因频率估计和标准差: pˆ ((2 3) 24) /(2 102) 0.1471 − = ×+ × = 1 2 0.1471 0.0294 2 0.1471 0.0256 2 102 S− = + −× = × ( ) 浙江大学 遗传学第十四章 17 欧洲不同人群中 CCR5 等位基因的频率估计值(标准差) 群体 观察值 基因型频率估计值 (标准差) 基因频率估计值 (标准差) 人 数 +/+ +/ Δ32 Δ32 /Δ32 +/+ +/ Δ32 Δ32 /Δ32 CCR5+ CCR5- Δ32 冰岛 102 75 24 3 0.7353 0.2353 0.0294 0.8529 0.1471 (0.0437) (0.0420) (0.0167) (0.0256) (0.0256) 英国 283 223 57 3 0.7880 0.2014 0.0106 0.8887 0.1113 (0.0243) (0.0238) (0.0061) (0.0131) (0.0131) 意大利 91 81 10 0 0.8901 0.1099 0.0000 0.9451 0.0549 (0.0328) (0.0328) (0.0000) (0.0164) (0.0164) 希腊 63 60 3 0 0.9524 0.0476 0.0000 0.9762 0.0238 (0.0268) (0.0268) (0.0000) (0.0134) (0.0134) +/+基因型: PS PS ˆ ˆ ++ ++ ++ ++ − = ≤≤+ = 1.96 0.6494 1.96 0.8209 P++ +/Δ32 基因型: PS PS ˆ ˆ +− +− +− +− − = ≤≤+ = 1.96 0.1530 1.96 0.3176 P+− Δ32/Δ32 基因型: ˆ ˆ PS PS −− −− −− − − =≤ ≤ + = 1.96 0 1.96 0.0622 P−− − CCR5+等位基因: pS pS ˆ ˆ 1.96 0.8029 1.96 0.9030 p ++ ++ − = ≤≤+ = + CCR5–Δ32 等位基因: pS pS ˆ ˆ 1.96 0.0970 1.96 0.1971 p −− −− − = ≤≤+ = − 欧洲4个地区不同人群CCR5基因的基因型频率和等位 基因频率的95%置信区间列于下表。 其中冰岛人群CCR5基因型频率和等位基因频率的95% 置信区间的估算如下:
3 浙江大学 遗传学第十四章 13 一般难以分析整个群体的所有个体 Î 就难以得到群体 基因型频率(P11、P12、P22)和等位基因频率(p1、p2)。 在群体中抽取一些个体 Î 样本群体 Î 计算基因型数 (n11、n12、n22)和等位基因数(n1、n2)Î 估算群体的 基因型频率( 、 、 )、等位基因频率( 、 )和 相应的标准差。 基因型频率或等位基因频率估计值的标准差 Î 度量 参数的抽样变异。 11 Pˆ 12 Pˆ 22 Pˆ 1 pˆ 2 pˆ 人类第3条染色体有一个细胞表层蛋白基因CCR5,该 基因座的编码区段有一个突变等位基因△32(缺失32bp)Î 正常型等位基因CCR5ª和突变型等位基因CCR5−△32。 3种基因型对爱滋病毒HIV的感染性不同,ª/ª易感染、 发病快,ª/△32易感染、发病慢,△32/△32不易感染。 下表列出了欧洲4个地区人群中 CCR5基因型观察值和基因型频率、 等位基因频率的估计值及其标准差 (Martinson 等,1997)。 浙江大学 遗传学第十四章 15 ①.ª/ª基因型频率估计和标准差: ˆ = 75 102 = 0.7353 P++ 0.7353 (1 0.7353) 0.0437 102 1 S++ = × × − = ②. ª/△32的基因型频率估计和标准差: 24 102 0.2353 Pˆ +− = = 0.2353 (1 0.2353) 0.0420 102 1 S+− = × × − = 以冰岛人群CCR5基因为例,计算基因型频率和 等位基因频率及其标准差: ③.Δ32/Δ32基因型频率估计和标准差: 0.0294 ˆ ˆ 1 Pˆ −− = − P++ − P+− = 0.0294 1 0.0294 0.0167 102 1 S−− = × ×( − )= ④. CCR5ª等位基因频率估计和标准差: pˆ 2 75 24 / 2 102 0.8529 + =( ) ×+ × = ( ) 1 2 0.8529 0.7353 2 0.8529 0.0256 2 102 S+ = + −× = × ( ) ⑤. CCR5-Δ32等位基因频率估计和标准差: pˆ ((2 3) 24) /(2 102) 0.1471 − = ×+ × = 1 2 0.1471 0.0294 2 0.1471 0.0256 2 102 S− = + −× = × ( ) 浙江大学 遗传学第十四章 17 欧洲不同人群中 CCR5 等位基因的频率估计值(标准差) 群体 观察值 基因型频率估计值 (标准差) 基因频率估计值 (标准差) 人 数 +/+ +/ Δ32 Δ32 /Δ32 +/+ +/ Δ32 Δ32 /Δ32 CCR5+ CCR5- Δ32 冰岛 102 75 24 3 0.7353 0.2353 0.0294 0.8529 0.1471 (0.0437) (0.0420) (0.0167) (0.0256) (0.0256) 英国 283 223 57 3 0.7880 0.2014 0.0106 0.8887 0.1113 (0.0243) (0.0238) (0.0061) (0.0131) (0.0131) 意大利 91 81 10 0 0.8901 0.1099 0.0000 0.9451 0.0549 (0.0328) (0.0328) (0.0000) (0.0164) (0.0164) 希腊 63 60 3 0 0.9524 0.0476 0.0000 0.9762 0.0238 (0.0268) (0.0268) (0.0000) (0.0134) (0.0134) +/+基因型: PS PS ˆ ˆ ++ ++ ++ ++ − = ≤≤+ = 1.96 0.6494 1.96 0.8209 P++ +/Δ32 基因型: PS PS ˆ ˆ +− +− +− +− − = ≤≤+ = 1.96 0.1530 1.96 0.3176 P+− Δ32/Δ32 基因型: ˆ ˆ PS PS −− −− −− − − =≤ ≤ + = 1.96 0 1.96 0.0622 P−− − CCR5+等位基因: pS pS ˆ ˆ 1.96 0.8029 1.96 0.9030 p ++ ++ − = ≤≤+ = + CCR5–Δ32 等位基因: pS pS ˆ ˆ 1.96 0.0970 1.96 0.1971 p −− −− − = ≤≤+ = − 欧洲4个地区不同人群CCR5基因的基因型频率和等位 基因频率的95%置信区间列于下表。 其中冰岛人群CCR5基因型频率和等位基因频率的95% 置信区间的估算如下:
4 浙江大学 遗传学第十四章 19 欧洲不同人群中CCR5基因的基因型频率和等位基因频率的95%置信区间 基因型 +/+ 基因型 +/Δ32 基因型 Δ32/Δ32 等位基因 CCR5+ 等位基因 CCR5-Δ32 群体 下限 上限 下限 上限 下限 上限 下限 上限 下限 上限 冰岛 0.6497 0.8209 0.1530 0.3176 0.0000 0.0622 0.8029 0.9030 0.0970 0.1971 英国 0.7404 0.8356 0.1547 0.2481 0.0000 0.0225 0.8630 0.9144 0.0856 0.1370 意大利 0.8259 0.9544 0.0456 0.1741 0.0000 0.0000 0.9129 0.9772 0.0228 0.0871 希腊 0.8998 1.0000 0.0000 0.1002 0.0000 0.0000 0.9499 1.0025 0.0000 0.0501 浙江大学 遗传学第十四章 20 置信区间的分析 Î 推断群体参数值的可能区间、比较 不同群体频率参数值的显著性差异。 例如,冰岛人群的+/+基因型频率上限(0.8209)大于 英国人群的下限(0.7404),但要小于意大利人群的下限 (0.8259)和希腊人群的下限(0.8998)Î 推断+/+基因型 频率在冰岛与英国人群之间无显著差异,但冰岛人群显著 低于意大利和希腊人群。 一对等位基因频率计算法 Î 推广到对一个遗传群体中 复等位基因(multiple alleles)的分析。 如果一个基因座上有k个复等位基因,则共有 k 个同质 基因型Ai Ai 和 k (k-1) / 2 个异质基因型Ai Aj 。 群体各种基因型为Nii(i=1,2,.,k)和Nij (i=1,2, .,k–1;j=i+1,i+2,.,k),基因型总数是: 样本群体各种基因型个体数分别是nii(i=1,2,.,k) 和nij (i=1,2,.,k–1;j=i+1,i+2,.,k ),基因型总数: ij k j i k i i k i N ∑Nii ∑ ∑ N = + − = = = + 1 1 1 ij k j i k i i k i ii n ∑n ∑ ∑ n = + − = = = + 1 1 1 浙江大学 遗传学第十四章 22 复等位基因的基因型频率计算公式 群体 样本群体 基因型 计数 基因型频率 计数 基因型频率估计 基因型频率估计标准误 Ai Ai Nii N N P ii ii = nii ˆ ii ii n P n = 1 ˆ ˆ ( (1 ) ii ii ii S PP n = − Ai Aj Nij N N P ij ij = nij ˆ ij ij n P n = 1 ˆ ˆ ( (1 ) ij ij ij S PP n = − 合计 N 1 n 1 浙江大学 遗传学第十四章 23 复等位基因频率的计算公式 群体 样本群体 基因型 计数 等位基因频率 计数 等位基因频率估计 等位基因频率估计标准误 Ai Ni 2 2 1 2 ii ij j i i ii ij j i N N p N p p ≠ ≠ + = = + ∑ ∑ ni 2 ˆ 2 1 ˆ ˆ 2 ii ij j i i ii ij j i n n p N p p ≠ ≠ + = = + ∑ ∑ 1 2 ˆ ( 2) ˆ ˆ 2 i i ii i S pP p n = +− 合计 2N 1 2n 1 浙江大学 遗传学第十四章 24 二、哈德-魏伯格定律
4 浙江大学 遗传学第十四章 19 欧洲不同人群中CCR5基因的基因型频率和等位基因频率的95%置信区间 基因型 +/+ 基因型 +/Δ32 基因型 Δ32/Δ32 等位基因 CCR5+ 等位基因 CCR5-Δ32 群体 下限 上限 下限 上限 下限 上限 下限 上限 下限 上限 冰岛 0.6497 0.8209 0.1530 0.3176 0.0000 0.0622 0.8029 0.9030 0.0970 0.1971 英国 0.7404 0.8356 0.1547 0.2481 0.0000 0.0225 0.8630 0.9144 0.0856 0.1370 意大利 0.8259 0.9544 0.0456 0.1741 0.0000 0.0000 0.9129 0.9772 0.0228 0.0871 希腊 0.8998 1.0000 0.0000 0.1002 0.0000 0.0000 0.9499 1.0025 0.0000 0.0501 浙江大学 遗传学第十四章 20 置信区间的分析 Î 推断群体参数值的可能区间、比较 不同群体频率参数值的显著性差异。 例如,冰岛人群的+/+基因型频率上限(0.8209)大于 英国人群的下限(0.7404),但要小于意大利人群的下限 (0.8259)和希腊人群的下限(0.8998)Î 推断+/+基因型 频率在冰岛与英国人群之间无显著差异,但冰岛人群显著 低于意大利和希腊人群。 一对等位基因频率计算法 Î 推广到对一个遗传群体中 复等位基因(multiple alleles)的分析。 如果一个基因座上有k个复等位基因,则共有 k 个同质 基因型Ai Ai 和 k (k-1) / 2 个异质基因型Ai Aj 。 群体各种基因型为Nii(i=1,2,.,k)和Nij (i=1,2, .,k–1;j=i+1,i+2,.,k),基因型总数是: 样本群体各种基因型个体数分别是nii(i=1,2,.,k) 和nij (i=1,2,.,k–1;j=i+1,i+2,.,k ),基因型总数: ij k j i k i i k i N ∑Nii ∑ ∑ N = + − = = = + 1 1 1 ij k j i k i i k i ii n ∑n ∑ ∑ n = + − = = = + 1 1 1 浙江大学 遗传学第十四章 22 复等位基因的基因型频率计算公式 群体 样本群体 基因型 计数 基因型频率 计数 基因型频率估计 基因型频率估计标准误 Ai Ai Nii N N P ii ii = nii ˆ ii ii n P n = 1 ˆ ˆ ( (1 ) ii ii ii S PP n = − Ai Aj Nij N N P ij ij = nij ˆ ij ij n P n = 1 ˆ ˆ ( (1 ) ij ij ij S PP n = − 合计 N 1 n 1 浙江大学 遗传学第十四章 23 复等位基因频率的计算公式 群体 样本群体 基因型 计数 等位基因频率 计数 等位基因频率估计 等位基因频率估计标准误 Ai Ni 2 2 1 2 ii ij j i i ii ij j i N N p N p p ≠ ≠ + = = + ∑ ∑ ni 2 ˆ 2 1 ˆ ˆ 2 ii ij j i i ii ij j i n n p N p p ≠ ≠ + = = + ∑ ∑ 1 2 ˆ ( 2) ˆ ˆ 2 i i ii i S pP p n = +− 合计 2N 1 2n 1 浙江大学 遗传学第十四章 24 二、哈德-魏伯格定律
5 浙江大学 遗传学第十四章 25 1. 概念:在一个完全随机交配的群体内,如果没有其它因素(如 突变、选择、迁移等),则基因频率和基因型频率可以 保持一定,各代不变。 设:在一个随机交配群内(即一个个体与群体内其它个体 交配机会相等),基因A1与A2的频率分别为p1和p2(p1+p2=1), 三种基因型的频率为: P11= p1 2, P12=2 p1p2, P22= p2 2 当3种不同基因型个体间充分随机交配 Î 下一代基因型频率 和亲代完全一样,不会发生改变。 这一现象由德国医生魏伯格(Weinberg W.)和英国数学家 哈德(Hardy G. H.)在1908年分别发现 Î 哈德-魏伯格定律。 浙江大学 遗传学第十四章 26 2. 验证: 设一群体内三个基因型频率是: A1A1 A1A2 A2A2 P11= p1 2, P12=2 p1p2, P22= p2 2 ∵这三种基因型产生配子频率为: A1: p1 2 + (1/2) (2 p1p2) = p1 (p1+p2) = p1 A2:(1/2) (2 p1p2) + p2 2 = p2 (p1+p2) = p2 在一个大群体中,个体间随机交配 Î 配子间的 随机结合 Î 可得以下结果: 浙江大学 遗传学第十四章 27 ♠下一代的3个基因型频率分别为 A1A1 A1A2 A2A2 P11= p1 2 P12=2 p1p2 P22= p2 2 ♠三个基因型频率和上一代频率完全一样。 ♠就这对基因而言,群体已经达到平衡。 雄配子(频率) 雌配子(频率) A1 (p1) A2 (p2) A1 (p1) A1A1 (p1 2 ) A1A2 (p1 p2) A2 (p2) A1A2 (p1 p2) A2A2 (p2 2 ) ①. 初始群体基因型频率:P11(0) =0.6,P12(0) =0.4,P22(0) =0 等位基因频率:p1(0) = P11(0) + (1/2) P12(0) =0.6 + (1/2) (0.4)=0.8 p2(0) = P22(0) + (1/2) P12(0) =0 + (1/2) (0.4)=0.2 3.例如: ②. 随机交配第一代基因型频率:P11(1) = p1 (0)2=0.82=0.64, P12(1) =2 p1 (0) p2 (0) =2×0.8×0.2=0.32, P22(1) = p2 (0)2 =0.22=0.04 等位基因频率:p1(1) = P11(1) + (1/2)P12(1) =0.64 + (1/2) (0.32)=0.8 P2(1) = P22(1) + (1/2)P12(1) =0.04 + (1/2) (0.32)=0.2 ③. 随机交配第二代基因型频率:P11(2) = p1 (1)2=0.82=0.64 , P12(2) =2 p1 (1) p2 (1)=2×0.8×0.2=0.32, P22(2) = p2 (1)2=0.22=0.04 等位基因频率:p1(2) = P11(2) + (1/2)P12(2) =0.64 + (1/2) (0.32)=0.8 p2(2) = P22(2) + (1/2)P12(2) =0.04 + (1/2) (0.32)=0.2 浙江大学 遗传学第十四章 29 ∴基因型频率 P11(1)≠ P11(0), P12(1)≠ P12(0), P22(1)≠ P22(0) 但经一代随机交配后,则 P11(1) = P11(2), P12(1) = P12(2), P22(1) = P22(2) 而等位基因频率则自始至终保持不变。 p1(0) = p1(1) = p1(2) , p2(0) = p2(1) = p2(2) 浙江大学 遗传学第十四章 30 4.定律要点:这一定律可以使一个群体的遗传特性保持 相对稳定。 ①.在随机交配的大群体中,如果没有其它因素干扰,则各代 基因频率能保持不变; ②.任何一个大群体内,不论原始等位基因频率和基因型频率 如何,只需经过一代的随机交配就可达到平衡。 ③.当一个群体达到平衡状态后,基因频率和基因型频率关系 是: P11= p1 2,P12=2 p1p2,P22= p2 2 。 自然界中许多群体都很大,个体间交配一般也是接近随机 Î 哈德-魏伯格定律基本上是普遍适用的
5 浙江大学 遗传学第十四章 25 1. 概念:在一个完全随机交配的群体内,如果没有其它因素(如 突变、选择、迁移等),则基因频率和基因型频率可以 保持一定,各代不变。 设:在一个随机交配群内(即一个个体与群体内其它个体 交配机会相等),基因A1与A2的频率分别为p1和p2(p1+p2=1), 三种基因型的频率为: P11= p1 2, P12=2 p1p2, P22= p2 2 当3种不同基因型个体间充分随机交配 Î 下一代基因型频率 和亲代完全一样,不会发生改变。 这一现象由德国医生魏伯格(Weinberg W.)和英国数学家 哈德(Hardy G. H.)在1908年分别发现 Î 哈德-魏伯格定律。 浙江大学 遗传学第十四章 26 2. 验证: 设一群体内三个基因型频率是: A1A1 A1A2 A2A2 P11= p1 2, P12=2 p1p2, P22= p2 2 ∵这三种基因型产生配子频率为: A1: p1 2 + (1/2) (2 p1p2) = p1 (p1+p2) = p1 A2:(1/2) (2 p1p2) + p2 2 = p2 (p1+p2) = p2 在一个大群体中,个体间随机交配 Î 配子间的 随机结合 Î 可得以下结果: 浙江大学 遗传学第十四章 27 ♠下一代的3个基因型频率分别为 A1A1 A1A2 A2A2 P11= p1 2 P12=2 p1p2 P22= p2 2 ♠三个基因型频率和上一代频率完全一样。 ♠就这对基因而言,群体已经达到平衡。 雄配子(频率) 雌配子(频率) A1 (p1) A2 (p2) A1 (p1) A1A1 (p1 2 ) A1A2 (p1 p2) A2 (p2) A1A2 (p1 p2) A2A2 (p2 2 ) ①. 初始群体基因型频率:P11(0) =0.6,P12(0) =0.4,P22(0) =0 等位基因频率:p1(0) = P11(0) + (1/2) P12(0) =0.6 + (1/2) (0.4)=0.8 p2(0) = P22(0) + (1/2) P12(0) =0 + (1/2) (0.4)=0.2 3.例如: ②. 随机交配第一代基因型频率:P11(1) = p1 (0)2=0.82=0.64, P12(1) =2 p1 (0) p2 (0) =2×0.8×0.2=0.32, P22(1) = p2 (0)2 =0.22=0.04 等位基因频率:p1(1) = P11(1) + (1/2)P12(1) =0.64 + (1/2) (0.32)=0.8 P2(1) = P22(1) + (1/2)P12(1) =0.04 + (1/2) (0.32)=0.2 ③. 随机交配第二代基因型频率:P11(2) = p1 (1)2=0.82=0.64 , P12(2) =2 p1 (1) p2 (1)=2×0.8×0.2=0.32, P22(2) = p2 (1)2=0.22=0.04 等位基因频率:p1(2) = P11(2) + (1/2)P12(2) =0.64 + (1/2) (0.32)=0.8 p2(2) = P22(2) + (1/2)P12(2) =0.04 + (1/2) (0.32)=0.2 浙江大学 遗传学第十四章 29 ∴基因型频率 P11(1)≠ P11(0), P12(1)≠ P12(0), P22(1)≠ P22(0) 但经一代随机交配后,则 P11(1) = P11(2), P12(1) = P12(2), P22(1) = P22(2) 而等位基因频率则自始至终保持不变。 p1(0) = p1(1) = p1(2) , p2(0) = p2(1) = p2(2) 浙江大学 遗传学第十四章 30 4.定律要点:这一定律可以使一个群体的遗传特性保持 相对稳定。 ①.在随机交配的大群体中,如果没有其它因素干扰,则各代 基因频率能保持不变; ②.任何一个大群体内,不论原始等位基因频率和基因型频率 如何,只需经过一代的随机交配就可达到平衡。 ③.当一个群体达到平衡状态后,基因频率和基因型频率关系 是: P11= p1 2,P12=2 p1p2,P22= p2 2 。 自然界中许多群体都很大,个体间交配一般也是接近随机 Î 哈德-魏伯格定律基本上是普遍适用的

6 浙江大学 遗传学第十四章 31 i p(i pi ) n S ˆ 1 ˆ 2 1 = − 如果随机交配群体的某基因座上有k个复等位基因, 则共有k个同质基因型Ai Ai 和k(k-1)/2个异质基因型Ai Aj 。 平衡群体中等位基因频率和基因型频率关系: Pii=pi 2(i=1,2,.,k-1),Pij=2pi pj (i=1,2,.,k; j=i+1,i+2, .,k)。 等位基因频率估计值的标准差: 哈德-魏伯格定律适用于复等位基因的群体。 浙江大学 遗传学第十四章 32 哈德-魏伯格定律对于那些不能用实验方法进行 研究的群体也具有适用性。 例如,早在1900年己发现人类血型遗传,但一直 到20年代哈德-魏伯格定律得到广泛应用后,才给予 合理的证明。 浙江大学 遗传学第十四章 33 等位基因 I O频率 po = POO 等位基因 I A频率 A A OO O p PP p = +− − 等位基因 I B频率 B A o p = 1− p − p ABO血型受单基因控制,该基因座具有3个复等位基因 (IA、IB和IO),其中IA和IB是共显性,IA和IB对IO是显性。 ∴ ABO血型有6种基因型和4种表现型,其相互关系可用 于估算复等位基因频率的计算公式: 浙江大学 遗传学第十四章 34 随机交配群体ABO血型的基因型和表现型关系 表现型 A B AB O 基因型 I A IA IA IO I B IB IB IO I A IB I O IO 基因型频率 2 A p A O 2 p p 2 B p B O 2 p p 2 pA pB 2 O p 表现型频率 A A A O P p 2 p p 2 − = + B B B O P p 2 p p 2 − = + PAB = 2 p A pB 2 POO = pO 浙江大学 遗传学第十四章 35 表现型 A B AB O 合计 个体数 n A− = 227 nB− = 91 nAB = 48 nOO = 134 500 表现型频率 0.454 Pˆ A− = 0.182 Pˆ B− = 0.096 Pˆ AB = 0.268 Pˆ OO = 1 一个人群中ABO血型的频率分析 4种表现型频率的估计值: Pˆ A− = nA− / n = 227 / 500 = 0.454, Pˆ B− = nB− / n = 91/ 500 = 0.182, ˆ ˆ / 48/ 500 0.096 / 134 / 500 0.268 P nn P nn AB AB OO OO == = == = , 现以一个人群ABO血型的调查资料为例,分析血型的 等位基因频率。 浙江大学 遗传学第十四章 36 3个等位基因频率的估计值和标准差: IO: ˆ ˆ 0.268 0.518 o OO p P == = ˆ ˆ (1 ) / 2 O OO S p pn = − = 0.518 × (1 − 0.518 ) 1000 = 0.016 IA: ˆ ˆ ˆ ˆ 0.454 0.268 0.518 0.332 A A OO O p PP p = + −= + − = − S = pˆ A (1 − pˆ A ) 2n = 0.332 × (1− 0.332) /1000 = 0.015 A IB:ˆ = 1 − ˆ − ˆ = 1 − 0.332 − 0.518 = 0.150 B A O p p p S = pˆ B (1 − pˆ B ) 2n = 0.150 × (1 − 0.150 ) / 1000 = 0.011 B
6 浙江大学 遗传学第十四章 31 i p(i pi ) n S ˆ 1 ˆ 2 1 = − 如果随机交配群体的某基因座上有k个复等位基因, 则共有k个同质基因型Ai Ai 和k(k-1)/2个异质基因型Ai Aj 。 平衡群体中等位基因频率和基因型频率关系: Pii=pi 2(i=1,2,.,k-1),Pij=2pi pj (i=1,2,.,k; j=i+1,i+2, .,k)。 等位基因频率估计值的标准差: 哈德-魏伯格定律适用于复等位基因的群体。 浙江大学 遗传学第十四章 32 哈德-魏伯格定律对于那些不能用实验方法进行 研究的群体也具有适用性。 例如,早在1900年己发现人类血型遗传,但一直 到20年代哈德-魏伯格定律得到广泛应用后,才给予 合理的证明。 浙江大学 遗传学第十四章 33 等位基因 I O频率 po = POO 等位基因 I A频率 A A OO O p PP p = +− − 等位基因 I B频率 B A o p = 1− p − p ABO血型受单基因控制,该基因座具有3个复等位基因 (IA、IB和IO),其中IA和IB是共显性,IA和IB对IO是显性。 ∴ ABO血型有6种基因型和4种表现型,其相互关系可用 于估算复等位基因频率的计算公式: 浙江大学 遗传学第十四章 34 随机交配群体ABO血型的基因型和表现型关系 表现型 A B AB O 基因型 I A IA IA IO I B IB IB IO I A IB I O IO 基因型频率 2 A p A O 2 p p 2 B p B O 2 p p 2 pA pB 2 O p 表现型频率 A A A O P p 2 p p 2 − = + B B B O P p 2 p p 2 − = + PAB = 2 p A pB 2 POO = pO 浙江大学 遗传学第十四章 35 表现型 A B AB O 合计 个体数 n A− = 227 nB− = 91 nAB = 48 nOO = 134 500 表现型频率 0.454 Pˆ A− = 0.182 Pˆ B− = 0.096 Pˆ AB = 0.268 Pˆ OO = 1 一个人群中ABO血型的频率分析 4种表现型频率的估计值: Pˆ A− = nA− / n = 227 / 500 = 0.454, Pˆ B− = nB− / n = 91/ 500 = 0.182, ˆ ˆ / 48/ 500 0.096 / 134 / 500 0.268 P nn P nn AB AB OO OO == = == = , 现以一个人群ABO血型的调查资料为例,分析血型的 等位基因频率。 浙江大学 遗传学第十四章 36 3个等位基因频率的估计值和标准差: IO: ˆ ˆ 0.268 0.518 o OO p P == = ˆ ˆ (1 ) / 2 O OO S p pn = − = 0.518 × (1 − 0.518 ) 1000 = 0.016 IA: ˆ ˆ ˆ ˆ 0.454 0.268 0.518 0.332 A A OO O p PP p = + −= + − = − S = pˆ A (1 − pˆ A ) 2n = 0.332 × (1− 0.332) /1000 = 0.015 A IB:ˆ = 1 − ˆ − ˆ = 1 − 0.332 − 0.518 = 0.150 B A O p p p S = pˆ B (1 − pˆ B ) 2n = 0.150 × (1 − 0.150 ) / 1000 = 0.011 B

7 浙江大学 遗传学第十四章 37 IO: IA: IB: ˆ ˆ 1.96 0.487 1.96 0.549 OO OO O pS pS − = ≤≤+ = p ˆ ˆ 1.96 0.303 1.96 0.361 AA AA A pS pS − = ≤≤+ = p ˆ 1.96 0.128 1.96 0.172 ˆ BB B B B pS p S − = ≤≤+ = p 利用等位基因频率的估计值和标准差,可计算基因 频率的95%置信区间 Î 推断群体基因频率的真值范围: 浙江大学 遗传学第十四章 38 5.定律意义: 哈德 – 魏伯格定律在群体遗传学中的重要性 Î 揭示 基因频率和基因型频率的规律。 只要群体内个体间能进行随机交配Î该群体能够保持 平衡状态和相对稳定。 即使由于突变、选择、迁移和杂交等因素改变了群体 的基因频率和基因型频率Î但只要这些因素不再继续产生 作用而进行随机交配时,则该群体仍将保持平衡。 浙江大学 遗传学第十四章 39 6.打破平衡的意义: 在人工控制下通过选择、杂交或人工诱变等途径, 就可以打破这种平衡 Î 促使生物个体发生变异 Î 群体 (如亚种、变种、品种或品系) 遗传特性将随之改变。 为动、植物育种中选育新类型提供了有利的条件。 ∴ 改变群体基因频率和基因型频率,打破遗传平衡Î 是目前动、植物育种中的主要手段。 浙江大学 遗传学第十四章 40 例:我国某人群中测定了1050人对苯硫脲的尝味能力,其中 410人(TT)有尝味能力、杂合的有 500人(Tt) 、味盲者有140 人(tt) 。 问是否是达到Hardy-weiberg平衡? T 的基因频率 p = (410×2+500)/(1050×2)=0.63 t 的基因频率 q = (140×2+500)/(1050×2)=0.37 TT Tt tt 总计 实际频数 (O) 410 500 140 1050 预计频数 (C) (Np2 ) 416.75 (N2 pq) 489.51 (Nq2 ) 143.74 N 1050 (O-C) 2 / C 0.109 0.225 0.097 0.431 χ2 = 0.431<3.841,符合Hardy-weiberg平衡群体。 浙江大学 遗传学第十四章 41 第二节 改变基因频率的因素 浙江大学 遗传学第十四章 42 在自然界或栽培条件下,许多因素可以影响群体 遗传平衡,如突变、选择、迁移和遗传漂变等,这些 因素都是促进生物进化的原因。 其中突变和选择是主要的
7 浙江大学 遗传学第十四章 37 IO: IA: IB: ˆ ˆ 1.96 0.487 1.96 0.549 OO OO O pS pS − = ≤≤+ = p ˆ ˆ 1.96 0.303 1.96 0.361 AA AA A pS pS − = ≤≤+ = p ˆ 1.96 0.128 1.96 0.172 ˆ BB B B B pS p S − = ≤≤+ = p 利用等位基因频率的估计值和标准差,可计算基因 频率的95%置信区间 Î 推断群体基因频率的真值范围: 浙江大学 遗传学第十四章 38 5.定律意义: 哈德 – 魏伯格定律在群体遗传学中的重要性 Î 揭示 基因频率和基因型频率的规律。 只要群体内个体间能进行随机交配Î该群体能够保持 平衡状态和相对稳定。 即使由于突变、选择、迁移和杂交等因素改变了群体 的基因频率和基因型频率Î但只要这些因素不再继续产生 作用而进行随机交配时,则该群体仍将保持平衡。 浙江大学 遗传学第十四章 39 6.打破平衡的意义: 在人工控制下通过选择、杂交或人工诱变等途径, 就可以打破这种平衡 Î 促使生物个体发生变异 Î 群体 (如亚种、变种、品种或品系) 遗传特性将随之改变。 为动、植物育种中选育新类型提供了有利的条件。 ∴ 改变群体基因频率和基因型频率,打破遗传平衡Î 是目前动、植物育种中的主要手段。 浙江大学 遗传学第十四章 40 例:我国某人群中测定了1050人对苯硫脲的尝味能力,其中 410人(TT)有尝味能力、杂合的有 500人(Tt) 、味盲者有140 人(tt) 。 问是否是达到Hardy-weiberg平衡? T 的基因频率 p = (410×2+500)/(1050×2)=0.63 t 的基因频率 q = (140×2+500)/(1050×2)=0.37 TT Tt tt 总计 实际频数 (O) 410 500 140 1050 预计频数 (C) (Np2 ) 416.75 (N2 pq) 489.51 (Nq2 ) 143.74 N 1050 (O-C) 2 / C 0.109 0.225 0.097 0.431 χ2 = 0.431<3.841,符合Hardy-weiberg平衡群体。 浙江大学 遗传学第十四章 41 第二节 改变基因频率的因素 浙江大学 遗传学第十四章 42 在自然界或栽培条件下,许多因素可以影响群体 遗传平衡,如突变、选择、迁移和遗传漂变等,这些 因素都是促进生物进化的原因。 其中突变和选择是主要的

8 浙江大学 遗传学第十四章 43 ①.提供自然选择的原始材料; ②.影响群体等位基因频率。 如:一对等位基因,当A1 Î A2时,群体中A1频率减少、 A2频率则增加。 长期A1 Î A2 ,最后该群体中A1将被A2代替 Î 这就是由于突变而产生的突变压。 一、突变(mutation): 1.基因突变对于改变群体遗传组成的作用: 浙江大学 遗传学第十四章 44 设:A1 Î A2为正突变,速率为u; A2 Î A1为反突变,速率为v。 某一世代中A2的频率为q,则A1的频率为p = 1– q。 平衡时,qv = pu = (1 – q) u qv = u – uq qv + uq = u q (v + u) = u ∴ q = u / (v + u) 同理可得: p = v / ( v + u) 2.当一个群体内正反突变压相等即平衡状态时: A1 A2 u v 3.当基因频率未达到平衡时: 群体中A1频率的改变值(△p) Î 是基因A2的突变频率(qv) 减去 基因A1的突变频率 (pu),即:△p = qv – pu。 例如:A1 → A2突变率为1 / 100万,突变频率u = 0.000001 A2 → A1突变率为0.5 / 100万,突变频率v = 0.0000005 则按上式可算出 pA = v / (v + u) = 0.0000005 / (0.0000005+0.000001)=0.33 以上说明,在群体中A1基因占33%,A2基因占67%。 当△p=0时,即qv=pu时,群体达到平衡; 当一对等位基因的正反突变速率相等(即v=u),则q和p的平衡值 为0.5。 浙江大学 遗传学第十四章 46 4.当A1 → A2的突变不受其它因素的阻碍,该群体最后将 达到纯合性的A2 : 设:基因A1的频率在某一世代是p0,则在n代之后,其频率 pn 将是: pn = p0 (1 – u)n 多数基因的突变率很小(1/104~1/107),仅靠突变压使 基因频率明显改变, 需要经过很多世代。 有些生物世代很短,突变压可能成为 一个重要因素。 浙江大学 遗传学第十四章 47 二、选择(selection): 1.基因突变对于改变群体遗传组成的作用: 例如:玉米致死基因: 设:正常绿色基因C和等位白苗基因 c 的基因频率为0.5。 经过一代繁殖,子代群体中将出现1/4隐性纯合体白苗, 死亡。 则:子代群体中的C频率变为2/3、c 频率只有1/3。 由此形成的下一代个体的频率为: 其中(1/3)2cc的白化苗个体又被淘汰。 cc 3 1 Cc : 3 1 3 2 CC: 2 3 2 2 2 × 浙江大学 遗传学第十四章 48 例如淘汰至第十代时: 0.8264CC: 0.1653Cc : 0.0083cc cc (10 1) 1 Cc : (10 1) 2 10 CC: (10 1) 10 2 2 2 2 = + + × + ∴ 第十代时,在100株苗中的白化苗 个体已不到1株 (0.83%)。 经 n 代淘汰后,群体内三种基因型的频率为: cc ( 1) 1 Cc : ( 1) 2 CC: ( 1) 2 2 2 2 + n + n + n n n
8 浙江大学 遗传学第十四章 43 ①.提供自然选择的原始材料; ②.影响群体等位基因频率。 如:一对等位基因,当A1 Î A2时,群体中A1频率减少、 A2频率则增加。 长期A1 Î A2 ,最后该群体中A1将被A2代替 Î 这就是由于突变而产生的突变压。 一、突变(mutation): 1.基因突变对于改变群体遗传组成的作用: 浙江大学 遗传学第十四章 44 设:A1 Î A2为正突变,速率为u; A2 Î A1为反突变,速率为v。 某一世代中A2的频率为q,则A1的频率为p = 1– q。 平衡时,qv = pu = (1 – q) u qv = u – uq qv + uq = u q (v + u) = u ∴ q = u / (v + u) 同理可得: p = v / ( v + u) 2.当一个群体内正反突变压相等即平衡状态时: A1 A2 u v 3.当基因频率未达到平衡时: 群体中A1频率的改变值(△p) Î 是基因A2的突变频率(qv) 减去 基因A1的突变频率 (pu),即:△p = qv – pu。 例如:A1 → A2突变率为1 / 100万,突变频率u = 0.000001 A2 → A1突变率为0.5 / 100万,突变频率v = 0.0000005 则按上式可算出 pA = v / (v + u) = 0.0000005 / (0.0000005+0.000001)=0.33 以上说明,在群体中A1基因占33%,A2基因占67%。 当△p=0时,即qv=pu时,群体达到平衡; 当一对等位基因的正反突变速率相等(即v=u),则q和p的平衡值 为0.5。 浙江大学 遗传学第十四章 46 4.当A1 → A2的突变不受其它因素的阻碍,该群体最后将 达到纯合性的A2 : 设:基因A1的频率在某一世代是p0,则在n代之后,其频率 pn 将是: pn = p0 (1 – u)n 多数基因的突变率很小(1/104~1/107),仅靠突变压使 基因频率明显改变, 需要经过很多世代。 有些生物世代很短,突变压可能成为 一个重要因素。 浙江大学 遗传学第十四章 47 二、选择(selection): 1.基因突变对于改变群体遗传组成的作用: 例如:玉米致死基因: 设:正常绿色基因C和等位白苗基因 c 的基因频率为0.5。 经过一代繁殖,子代群体中将出现1/4隐性纯合体白苗, 死亡。 则:子代群体中的C频率变为2/3、c 频率只有1/3。 由此形成的下一代个体的频率为: 其中(1/3)2cc的白化苗个体又被淘汰。 cc 3 1 Cc : 3 1 3 2 CC: 2 3 2 2 2 × 浙江大学 遗传学第十四章 48 例如淘汰至第十代时: 0.8264CC: 0.1653Cc : 0.0083cc cc (10 1) 1 Cc : (10 1) 2 10 CC: (10 1) 10 2 2 2 2 = + + × + ∴ 第十代时,在100株苗中的白化苗 个体已不到1株 (0.83%)。 经 n 代淘汰后,群体内三种基因型的频率为: cc ( 1) 1 Cc : ( 1) 2 CC: ( 1) 2 2 2 2 + n + n + n n n
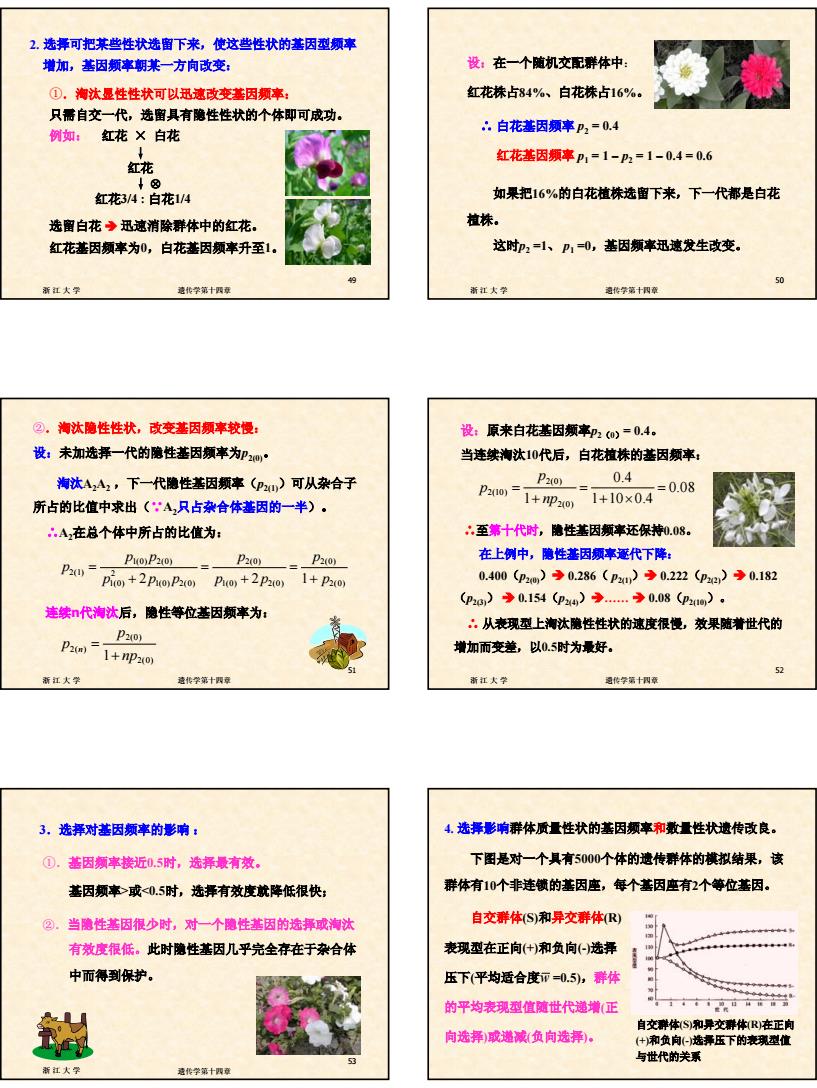
9 浙江大学 遗传学第十四章 49 2. 选择可把某些性状选留下来,使这些性状的基因型频率 增加,基因频率朝某一方向改变: ①.淘汰显性性状可以迅速改变基因频率: 只需自交一代,选留具有隐性性状的个体即可成功。 例如: 红花 × 白花 ↓ 红花 ↓ ⊗ 红花3/4 : 白花1/4 选留白花 Î 迅速消除群体中的红花。 红花基因频率为0,白花基因频率升至1。 浙江大学 遗传学第十四章 50 设:在一个随机交配群体中: 红花株占84%、白花株占16%。 ∴ 白花基因频率 p2 = 0.4 红花基因频率 p1 = 1 – p2 = 1 – 0.4 = 0.6 如果把16%的白花植株选留下来,下一代都是白花 植株。 这时p2 =1、 p1 =0,基因频率迅速发生改变。 浙江大学 遗传学第十四章 51 ②.淘汰隐性性状,改变基因频率较慢: 设:未加选择一代的隐性基因频率为p2(0)。 淘汰A2A2 ,下一代隐性基因频率(p2(1))可从杂合子 所占的比值中求出(∵A2只占杂合体基因的一半)。 ∴A2在总个体中所占的比值为: 1(0) 2(0) 2(0) 2(0) 2(1) 2 1(0) 1(0) 2(0) 1(0) 2(0) 2(0) 2 21 pp p p p p pp p p p = == + ++ 连续n代淘汰后,隐性等位基因频率为: 2(0) 2(0) 2( ) 1 np p p n + = 浙江大学 遗传学第十四章 52 设:原来白花基因频率p2(0)= 0.4。 当连续淘汰10代后,白花植株的基因频率: 0.08 1 10 0.4 0.4 1 2(0) 2(0) 2(10) = + × = + = np p p ∴至第十代时,隐性基因频率还保持0.08。 在上例中,隐性基因频率逐代下降: 0.400(p2(0))Î 0.286( p2(1))Î 0.222(p2(2))Î 0.182 (p2(3)) Î 0.154(p2(4))Î. Î 0.08(p2(10))。 ∴ 从表现型上淘汰隐性性状的速度很慢,效果随着世代的 增加而变差,以0.5时为最好。 浙江大学 遗传学第十四章 53 3.选择对基因频率的影响 : ①.基因频率接近0.5时,选择最有效。 基因频率>或<0.5时,选择有效度就降低很快; ②.当隐性基因很少时,对一个隐性基因的选择或淘汰 有效度很低。此时隐性基因几乎完全存在于杂合体 中而得到保护。 4. 选择影响群体质量性状的基因频率和数量性状遗传改良。 下图是对一个具有5000个体的遗传群体的模拟结果,该 群体有10个非连锁的基因座,每个基因座有2个等位基因。 自交群体(S)和异交群体(R) 表现型在正向(+)和负向(-)选择 压下(平均适合度 =0.5),群体 的平均表现型值随世代递增(正 向选择)或递减(负向选择)。 自交群体(S)和异交群体(R)在正向 (+)和负向(-)选择压下的表现型值 与世代的关系 w
9 浙江大学 遗传学第十四章 49 2. 选择可把某些性状选留下来,使这些性状的基因型频率 增加,基因频率朝某一方向改变: ①.淘汰显性性状可以迅速改变基因频率: 只需自交一代,选留具有隐性性状的个体即可成功。 例如: 红花 × 白花 ↓ 红花 ↓ ⊗ 红花3/4 : 白花1/4 选留白花 Î 迅速消除群体中的红花。 红花基因频率为0,白花基因频率升至1。 浙江大学 遗传学第十四章 50 设:在一个随机交配群体中: 红花株占84%、白花株占16%。 ∴ 白花基因频率 p2 = 0.4 红花基因频率 p1 = 1 – p2 = 1 – 0.4 = 0.6 如果把16%的白花植株选留下来,下一代都是白花 植株。 这时p2 =1、 p1 =0,基因频率迅速发生改变。 浙江大学 遗传学第十四章 51 ②.淘汰隐性性状,改变基因频率较慢: 设:未加选择一代的隐性基因频率为p2(0)。 淘汰A2A2 ,下一代隐性基因频率(p2(1))可从杂合子 所占的比值中求出(∵A2只占杂合体基因的一半)。 ∴A2在总个体中所占的比值为: 1(0) 2(0) 2(0) 2(0) 2(1) 2 1(0) 1(0) 2(0) 1(0) 2(0) 2(0) 2 21 pp p p p p pp p p p = == + ++ 连续n代淘汰后,隐性等位基因频率为: 2(0) 2(0) 2( ) 1 np p p n + = 浙江大学 遗传学第十四章 52 设:原来白花基因频率p2(0)= 0.4。 当连续淘汰10代后,白花植株的基因频率: 0.08 1 10 0.4 0.4 1 2(0) 2(0) 2(10) = + × = + = np p p ∴至第十代时,隐性基因频率还保持0.08。 在上例中,隐性基因频率逐代下降: 0.400(p2(0))Î 0.286( p2(1))Î 0.222(p2(2))Î 0.182 (p2(3)) Î 0.154(p2(4))Î. Î 0.08(p2(10))。 ∴ 从表现型上淘汰隐性性状的速度很慢,效果随着世代的 增加而变差,以0.5时为最好。 浙江大学 遗传学第十四章 53 3.选择对基因频率的影响 : ①.基因频率接近0.5时,选择最有效。 基因频率>或<0.5时,选择有效度就降低很快; ②.当隐性基因很少时,对一个隐性基因的选择或淘汰 有效度很低。此时隐性基因几乎完全存在于杂合体 中而得到保护。 4. 选择影响群体质量性状的基因频率和数量性状遗传改良。 下图是对一个具有5000个体的遗传群体的模拟结果,该 群体有10个非连锁的基因座,每个基因座有2个等位基因。 自交群体(S)和异交群体(R) 表现型在正向(+)和负向(-)选择 压下(平均适合度 =0.5),群体 的平均表现型值随世代递增(正 向选择)或递减(负向选择)。 自交群体(S)和异交群体(R)在正向 (+)和负向(-)选择压下的表现型值 与世代的关系 w
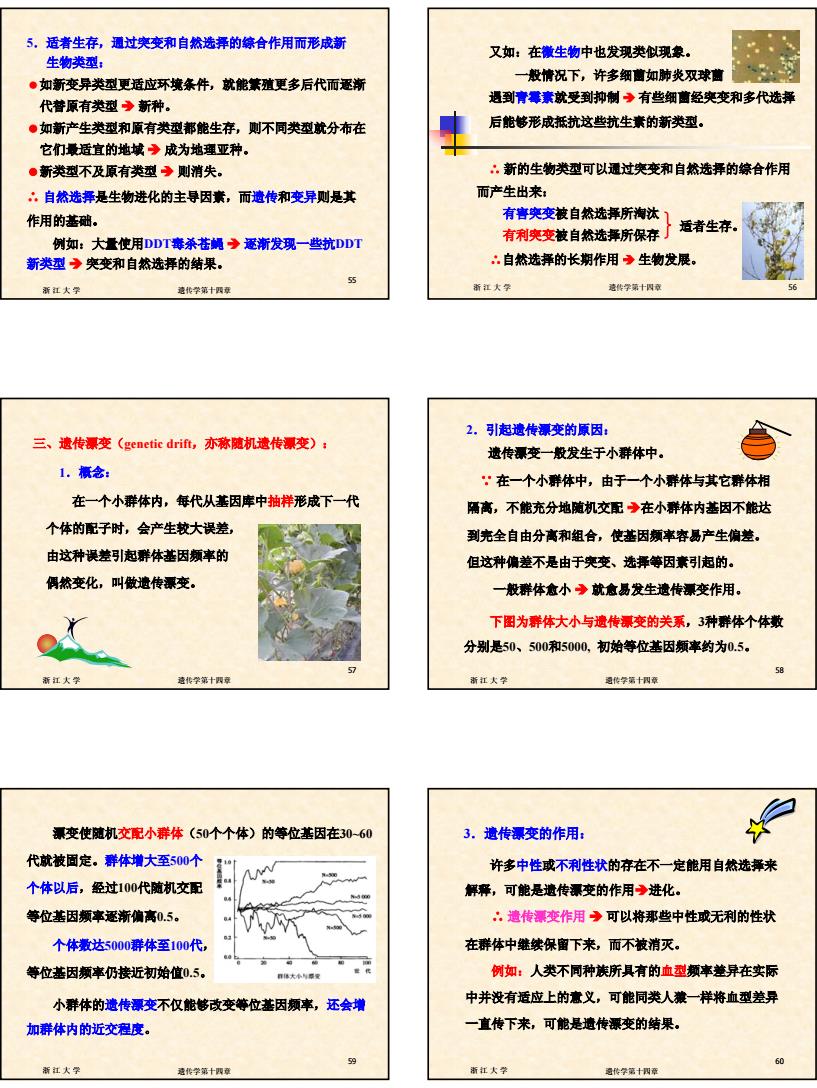
10 浙江大学 遗传学第十四章 55 5.适者生存,通过突变和自然选择的综合作用而形成新 生物类型: 如新变异类型更适应环境条件,就能繁殖更多后代而逐渐 代替原有类型 Î 新种。 如新产生类型和原有类型都能生存,则不同类型就分布在 它们最适宜的地域 Î 成为地理亚种。 新类型不及原有类型 Î 则消失。 ∴ 自然选择是生物进化的主导因素,而遗传和变异则是其 作用的基础。 例如:大量使用DDT毒杀苍蝇 Î 逐渐发现一些抗DDT 新类型 Î 突变和自然选择的结果。 浙江大学 遗传学第十四章 56 又如:在微生物中也发现类似现象。 一般情况下,许多细菌如肺炎双球菌 遇到青霉素就受到抑制 Î 有些细菌经突变和多代选择 后能够形成抵抗这些抗生素的新类型。 ∴ 新的生物类型可以通过突变和自然选择的综合作用 而产生出来: 有害突变被自然选择所淘汰 有利突变被自然选择所保存 ∴自然选择的长期作用 Î 生物发展。 适者生存。 浙江大学 遗传学第十四章 57 三、遗传漂变(genetic drift,亦称随机遗传漂变): 1.概念: 在一个小群体内,每代从基因库中抽样形成下一代 个体的配子时,会产生较大误差, 由这种误差引起群体基因频率的 偶然变化,叫做遗传漂变。 浙江大学 遗传学第十四章 58 2.引起遗传漂变的原因: 遗传漂变一般发生于小群体中。 ∵ 在一个小群体中,由于一个小群体与其它群体相 隔离,不能充分地随机交配 Î在小群体内基因不能达 到完全自由分离和组合,使基因频率容易产生偏差。 但这种偏差不是由于突变、选择等因素引起的。 一般群体愈小 Î 就愈易发生遗传漂变作用。 下图为群体大小与遗传漂变的关系,3种群体个体数 分别是50、500和5000, 初始等位基因频率约为0.5。 浙江大学 遗传学第十四章 59 漂变使随机交配小群体(50个个体)的等位基因在30~60 代就被固定。群体增大至500个 个体以后,经过100代随机交配 等位基因频率逐渐偏离0.5。 个体数达5000群体至100代, 等位基因频率仍接近初始值0.5。 小群体的遗传漂变不仅能够改变等位基因频率,还会增 加群体内的近交程度。 浙江大学 遗传学第十四章 60 3.遗传漂变的作用: 许多中性或不利性状的存在不一定能用自然选择来 解释,可能是遗传漂变的作用Î进化。 ∴ 遗传漂变作用 Î 可以将那些中性或无利的性状 在群体中继续保留下来,而不被消灭。 例如:人类不同种族所具有的血型频率差异在实际 中并没有适应上的意义,可能同类人猿一样将血型差异 一直传下来,可能是遗传漂变的结果
10 浙江大学 遗传学第十四章 55 5.适者生存,通过突变和自然选择的综合作用而形成新 生物类型: 如新变异类型更适应环境条件,就能繁殖更多后代而逐渐 代替原有类型 Î 新种。 如新产生类型和原有类型都能生存,则不同类型就分布在 它们最适宜的地域 Î 成为地理亚种。 新类型不及原有类型 Î 则消失。 ∴ 自然选择是生物进化的主导因素,而遗传和变异则是其 作用的基础。 例如:大量使用DDT毒杀苍蝇 Î 逐渐发现一些抗DDT 新类型 Î 突变和自然选择的结果。 浙江大学 遗传学第十四章 56 又如:在微生物中也发现类似现象。 一般情况下,许多细菌如肺炎双球菌 遇到青霉素就受到抑制 Î 有些细菌经突变和多代选择 后能够形成抵抗这些抗生素的新类型。 ∴ 新的生物类型可以通过突变和自然选择的综合作用 而产生出来: 有害突变被自然选择所淘汰 有利突变被自然选择所保存 ∴自然选择的长期作用 Î 生物发展。 适者生存。 浙江大学 遗传学第十四章 57 三、遗传漂变(genetic drift,亦称随机遗传漂变): 1.概念: 在一个小群体内,每代从基因库中抽样形成下一代 个体的配子时,会产生较大误差, 由这种误差引起群体基因频率的 偶然变化,叫做遗传漂变。 浙江大学 遗传学第十四章 58 2.引起遗传漂变的原因: 遗传漂变一般发生于小群体中。 ∵ 在一个小群体中,由于一个小群体与其它群体相 隔离,不能充分地随机交配 Î在小群体内基因不能达 到完全自由分离和组合,使基因频率容易产生偏差。 但这种偏差不是由于突变、选择等因素引起的。 一般群体愈小 Î 就愈易发生遗传漂变作用。 下图为群体大小与遗传漂变的关系,3种群体个体数 分别是50、500和5000, 初始等位基因频率约为0.5。 浙江大学 遗传学第十四章 59 漂变使随机交配小群体(50个个体)的等位基因在30~60 代就被固定。群体增大至500个 个体以后,经过100代随机交配 等位基因频率逐渐偏离0.5。 个体数达5000群体至100代, 等位基因频率仍接近初始值0.5。 小群体的遗传漂变不仅能够改变等位基因频率,还会增 加群体内的近交程度。 浙江大学 遗传学第十四章 60 3.遗传漂变的作用: 许多中性或不利性状的存在不一定能用自然选择来 解释,可能是遗传漂变的作用Î进化。 ∴ 遗传漂变作用 Î 可以将那些中性或无利的性状 在群体中继续保留下来,而不被消灭。 例如:人类不同种族所具有的血型频率差异在实际 中并没有适应上的意义,可能同类人猿一样将血型差异 一直传下来,可能是遗传漂变的结果