
里德伯常数的测定 氢原子的光谱现在按波长(或波数)大小的排列次序上显示出简单的规律性, 测量氢灯各光谱线的波长值可以来了解原子的能级结构。本实验用分光计测量氢 原子的光谱线波长,并通过巴尔末公式推算里德伯常数。 原理 氢原子的光谱线在可见光区共有四条,分别用H。(红线)H。(蓝绿线)H (青线)和H,(紫线)记号来标志。他们的波数y(波长元的倒数)可以准确 地用实验公式 (1) 表示,式中n是大于2的整数,即3,4,5,…每一个数代表一条谱线,而R,是 一个实验常数,称为里德伯常数。式(1)就是著名的巴尔末公式。若利用分光 计准确的测定上述四条谱线的波长,并分别代入(1)式,即可由实验方法确定 里德伯常数。此外,根据玻尔关于原子构造的量子假设,里德伯常数与原子内部 若干微观量和有关物理普适常数的关系是: RH e m (2) 8ceih(1+m) MH 式中e为电子电荷,m为电子质量,Mn为氢原子核的质量,m 1 g1836.5’C 为光在真空中的传播速度,6。为真空介电常数,h为普朗克常数。由此算出里德 伯常数的理论值 Rg=1.09678×10/m 实验内容 1、以钠灯为光源,利用分光计及光栅测出衍射角,再算得光栅常数。 2、用氢气放电管作为光源,分别测出氢原子三条谱线(H。,H。,H,)所对
里德伯常数的测定 氢原子的光谱现在按波长(或波数)大小的排列次序上显示出简单的规律性, 测量氢灯各光谱线的波长值可以来了解原子的能级结构。本实验用分光计测量氢 原子的光谱线波长,并通过巴尔末公式推算里德伯常数。 原理 氢原子的光谱线在可见光区共有四条,分别用 α(红线)Hβ (蓝绿线) (青线)和 (紫线)记号来标志。他们的波数 H Hγ Hδ ν (波长λ 的倒数)可以准确 地用实验公式 ) 1 2 1 ( 22 n ν RH −= (1) 表示,式中 n 是大于 2 的整数,即 3,4,5,…每一个数代表一条谱线,而 RH 是 一个实验常数,称为里德伯常数。式(1)就是著名的巴尔末公式。若利用分光 计准确的测定上述四条谱线的波长,并分别代入(1)式,即可由实验方法确定 里德伯常数。此外,根据玻尔关于原子构造的量子假设,里德伯常数与原子内部 若干微观量和有关物理普适常数的关系是: )1( 8 32 0 4 H H M m m hce e R + = (2) 式中 e 为电子电荷,m 为电子质量,M H 为氢原子核的质量, 5.1836 1 = M H m ,c 为光在真空中的传播速度, 0 ε 为真空介电常数,h 为普朗克常数。由此算出里德 伯常数的理论值 RH /1009678.1 m 7 ×= 实验内容 1﹑以钠灯为光源,利用分光计及光栅测出衍射角,再算得光栅常数。 2﹑用氢气放电管作为光源,分别测出氢原子三条谱线( Hα, , Hβ Hγ )所对
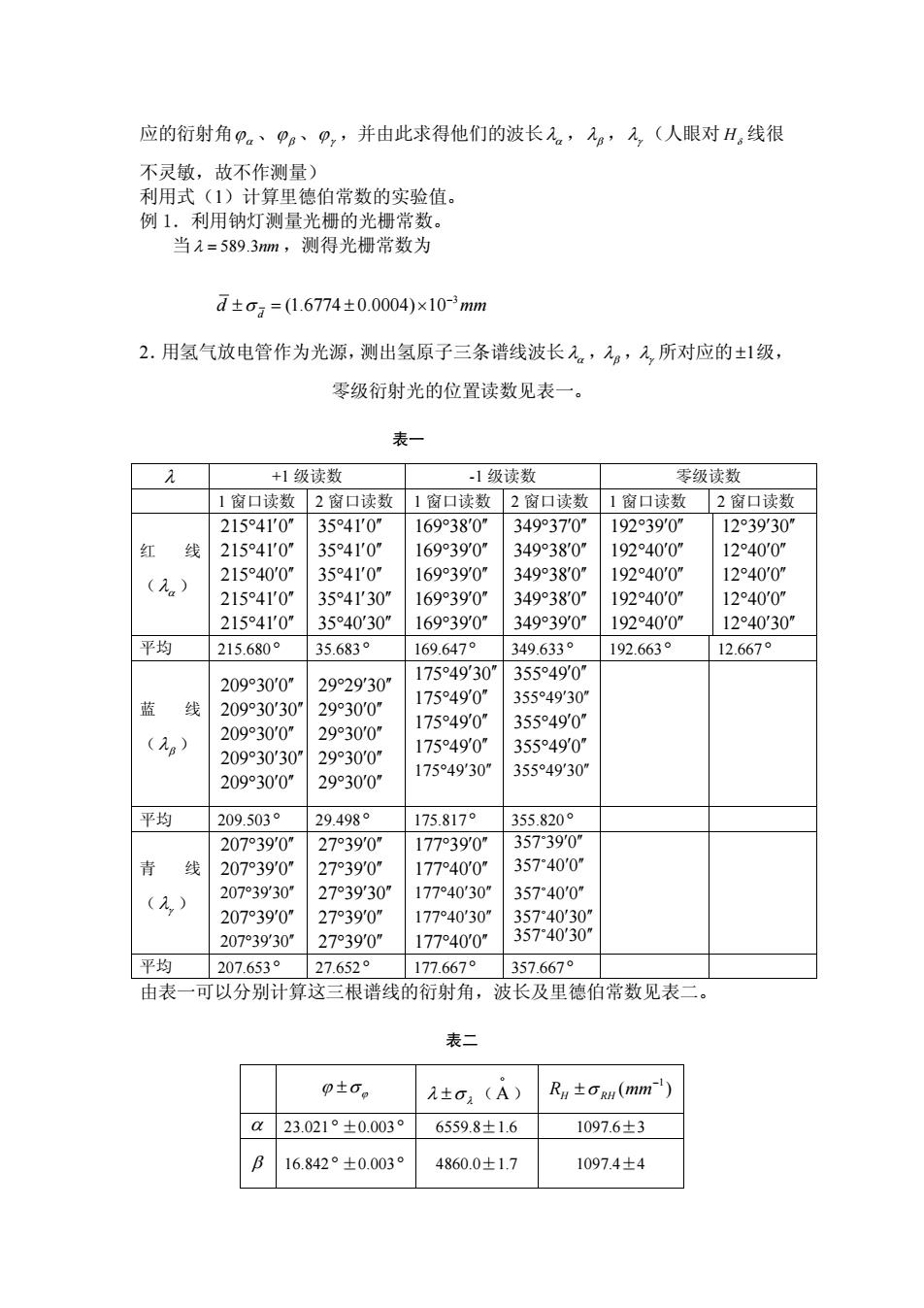
应的衍射角p。、p。、p,并由此求得他们的波长,p,入,(人眼对H,线很 不灵敏,故不作测量) 利用式(1)计算里德伯常数的实验值。 例1.利用钠灯测量光栅的光栅常数。 当1=589.3m,测得光栅常数为 d±og=(1.6774±0.0004)×10-3mm 2.用氢气放电管作为光源,测出氢原子三条谱线波长元,,元,所对应的±1级, 零级衍射光的位置读数见表一。 表一 +1级读数 -1级读数 零级读数 1窗口读数 2窗口读数 1窗口读数 2窗口读数 1窗口读数 2窗口读数 215410" 3541'0" 16938'0" 349°370" 19239'0" 123930" 红 线 21541'0" 3541'0" 169°390" 34938'0" 19240'0" 12°40'0" (a) 215°40'0" 3541'0" 16939'0" 34938'0" 19240'0" 12°40'0" 21541'0" 3541'30" 16939'0" 34938'0" 19240'0" 12°40'0" 215410" 3540'30" 16939'0" 349°390" 192°40'0" 12°40'30" 平均 215.680° 35.683° 169.647° 349.633° 192.663 12.667° 20930'0" 17549'30" 35549'0" 292930" 17549'0" 3554930" 蓝 线 20930'30" 2930'0" 17549'0" 35549'0" (B) 20930'0" 2930'0" 17549'0" 35549'0" 209°30'30" 2930'0" 1754930" 355°49'30" 20930'0" 2930'0" 平均 209.503° 29.498° 175.817° 355.820° 20739'0" 2739'0" 17739'0" 35739'0" 青 线 20739'0" 2739'0" 177°40'0" 35740'0" 207°39'30” (元,) 2739'30" 177°40'30” 35740'0" 20739'0" 27°39'0" 177°40'30” 357°40'30 20739'30” 2739'0" 177°40'0" 35740'30" 平均 207.653° 27.652° 177.667 357.667 由表一可以分别计算这三根谱线的衍射角, 波长及里德伯常数见表二。 表二 p±0。 元±o:(A) Rg±Og(mm) 23.021°±0.003° 6559.8±1.6 1097.6±3 16.842°±0.003° 4860.0±1.7 1097.4±4
应的衍射角ϕ α、ϕ β、ϕγ ,并由此求得他们的波长λα ,λβ,λγ(人眼对 线很 不灵敏,故不作测量) Hδ 利用式(1)计算里德伯常数的实验值。 例 1.利用钠灯测量光栅的光栅常数。 当λ = 3.589 nm ,测得光栅常数为 3 (1.6774 0.0004) 10 d d m σ − ±= ± × m 2.用氢气放电管作为光源,测出氢原子三条谱线波长λα ,λβ,λγ 所对应的 级, 零级衍射光的位置读数见表一。 ±1 表一 λ +1 级读数 -1 级读数 零级读数 1 窗口读数 2 窗口读数 1 窗口读数 2 窗口读数 1 窗口读数 2 窗口读数 红 线 (λα ) 215 41 0 ° ′ ′′ 215 41 0 ° ′ ′′ 215 40 0 ° ′ ′′ 215 41 0 ° ′ ′′ 215 41 0 ° ′ ′′ 35 41 0 ° ′ ′′ 35 41 0 ° ′ ′′ 35 41 0 ° ′ ′′ 35 41 30 ° ′ ′ 35 40 30 ′ ′ ′ ° ′ 169 38 0 ° ′ ′′ 169 39 0 ° ′ ′′ 169 39 0 ° ′ ′′ 169 39 0 ° ′ ′′ 169 39 0 ° ′ ′′ 349 37 0 ° ′ ′′ 349 38 0 ° ′ ′′ 349 38 0 ° ′ ′′ 349 38 0 ° ′ ′′ 349 39 0 ° ′ ′′ 192 39 0 ° ′ ′′ 192 40 0 ° ′ ′′ 192 40 0 ° ′ ′′ 192 40 0 ° ′ ′′ 192 40 0 ° ′ ′′ 12 39 30 ° ′ ′′ 12 40 0 ° ′ ′′ 12 40 0 ° ′ ′′ 12 40 0 ° ′ ′′ 12 40 30 ° ′ ′′ 平均 215.680 ° 35.683 ° 169.647 ° 349.633 ° 192.663 ° 12.667 ° 蓝 线 ( 175 49 30 ′ λβ ) 209 30 0 ° ′ ′′ 209 30 30 ° ′ ′′ 209 30 0 ° ′ ′′ 209 30 30 ° ′ ′′ 209 30 0 ° ′ ′′ 29 29 30 ° ′ ′′ 29 30 0 ° ′ ′′ 29 30 0 ° ′ ′′ 29 30 0 ° ′ ′′ 29 30 0 ° ′ ′′ ° ′′ 175 49 0 ° ′ ′′ 175 49 0 ° ′ ′′ 175 49 0 ° ′ ′′ 175 49 30 ° ′ ′′ 355 49 0 ° ′ ′′ 355 49 30 ° ′ ′′ 355 49 0 ° ′ ′′ 355 49 0 ° ′ ′′ 355 49 30 ° ′ ′′ 平均 209.503 ° 29.498 ° 175.817 ° 355.820 ° 青 线 (λγ ) 207 39 0 ° ′ ′′ 207 39 0 ° ′ ′′ 207 39 30 ° ′ ′′ 207 39 0 ° ′ ′′ 207 39 30 ° ′ ′′ 27 39 0 ° ′ ′′ 27 39 0 ° ′ ′′ 27 39 30 ° ′ ′′ 27 39 0 ° ′ ′′ 27 39 0 ° ′ ′′ 177 39 0 ° ′ ′′ 177 40 0 ° ′ ′′ 177 40 30 ° ′ ′′ 177 40 30 ° ′ ′′ 177 40 0 ° ′ ′′ 093357 ′′′ o 004357 ′′′ o 004357 ′′′ o 0304357 ′′′ o 0304357 ′′′ o 平均 207.653 ° 27.652 ° 177.667 ° 357.667 ° 由表一可以分别计算这三根谱线的衍射角,波长及里德伯常数见表二。 表二 ϕ ±σ ϕ λ ±σ λ( )A o 1 ( ) RH RH σ mm− ± α 23.021 ° ±0.003 ° 6559.8±1.6 1097.6±3 β 16.842 ° ±0.003 ° 4860.0±1.7 1097.4±4

Y14.944°±0.003°4339.7±1.7 1097.3±4 R,的平均值及标准偏差为 Ru±o元=(1.0975±0.0001)×10'/m。 思考题 1.氢原子在可见区、红外区、紫外区的所有谱线可统一用一个简单的公式表示: 11 立=R元灵 式中n=l、2、3、…;n=nm+1、n+2…。根据什么原则来选定各氢光谱线的 n的可能值?又怎么来判别某个n值的可能值是正确值?n又怎么求得呢?(提 示:可作-】图线来判断所选定n的正确性及求得n) 2.光谱中若出现不属于氢的谱线,应如何判断?
γ 14.944 ° ±0.003 ° 4339.7±1.7 1097.3±4 RH 的平均值及标准偏差为 7 ˆ (1.0975 0.0001) 10 / H R R m ±= ± × σ 。 思考题 1. 氢原子在可见区、红外区、紫外区的所有谱线可统一用一个简单的公式表示: 2 2 1 1 ( ) H oi R n n ν% = − 式中 =1﹑2﹑3﹑… ;n= +1﹑ +2…。根据什么原则来选定各氢光谱线的 n 的可能值?又怎么来判别某个 n 值的可能值是正确值? 又怎么求得呢?(提 示:可作 oi n oi n oi n oi n 2 1 n ν% − 图线来判断所选定 n 的正确性及求得 。)oi n 2.光谱中若出现不属于氢的谱线,应如何判断?