
金属逸出电势的测定 电子从加热的金属中发射出来的现象称为热电子发射。热电子发射的性能与金属材料 的逸出电势(或逸出功)有关。在电真空器件阴极材料的选择中,材料的逸出电势是重要 参量之一。本实验用理查逊(Richardsion)直线法测量钨的逸出电势,这一方法有丰富的 物理思想和较好的数据处理基本训练。 【实验目的】 1.了解有关热电子发射的基本规律。 2.用理查逊直线法测定钨丝的电子逸出电势V。 3.进一步学习数据处理方法。 【实验原理】 在高真空(1.33×104Pa以下)的电子管中,一个由被测金属丝做成的阴极K,通过电 流缸加热,并在另一个阳极加正电压时,在连接这两个电极的外电路中将有电流1通过,如 图1,所示这种现象称为热电子发射。 通过对热电子发射规律的研究,可以测定阴极材料逸出功,以选择合适的材料。 (1)电子的逸出功、逸出电势 根据固体物理中金属电子理论,金属中传导电子的能量分布是按费米一狄拉克分布 (Fermi--Dirac distribution)的。即 f(E)=dN_4n dE(2m)Ev(e E-Eg (1) 式中,E为费米能级。 在绝对零度时能量分布如图2中曲线(1)所示。此时,电子具有最大动能E。当温度 升高时,电子能量分布曲线如图2中曲线(2)所示。其中能量较大的少数电子具有比E更 高的能量,且具有这种能量的电子数随能量的增加而指数递减。 E◆ () dN/dE 0 图1 图2 在通常温度下由于金属表面存在一个厚约1010m左右的电子层一正电荷的偶电层, 它的电场阻碍电子从金属表面逸出,也就是说金属表面与外界(真空)之间存在一个势垒
金属逸出电势的测定 电子从加热的金属中发射出来的现象称为热电子发射。热电子发射的性能与金属材料 的逸出电势(或逸出功)有关。在电真空器件阴极材料的选择中,材料的逸出电势是重要 参量之一。本实验用理查逊(Richardsion)直线法测量钨的逸出电势,这一方法有丰富的 物理思想和较好的数据处理基本训练。 【实验目的】 1. 了解有关热电子发射的基本规律。 2. 用理查逊直线法测定钨丝的电子逸出电势 V。 3. 进一步学习数据处理方法。 【实验原理】 在高真空(1.33×10-4Pa以下)的电子管中,一个由被测金属丝做成的阴极K,通过电 流If加热,并在另一个阳极加正电压时,在连接这两个电极的外电路中将有电流Ia通过,如 图 1,所示这种现象称为热电子发射。 通过对热电子发射规律的研究,可以测定阴极材料逸出功,以选择合适的材料。 (1) 电子的逸出功、逸出电势 根据固体物理中金属电子理论,金属中传导电子的能量分布是按费米—狄拉克分布 (Fermi—Dirac distribution)的。即 2/12/3 1 3 )1()2( 4 )( − − == + kT EE F eEm hdE dN Ef π (1) 式中,EF为费米能级。 在绝对零度时能量分布如图 2 中曲线(1)所示。此时,电子具有最大动能EF。当温度 升高时,电子能量分布曲线如图 2 中曲线(2)所示。其中能量较大的少数电子具有比EF更 高的能量,且具有这种能量的电子数随能量的增加而指数递减。 Ia μ A K Ua Uf If A 图 1 EF Eb Eb dN/dE O E0 (1) X (2) E 图 2 在通常温度下由于金属表面存在一个厚约 10-10 m左右的电子层——正电荷的偶电层, 它的电场阻碍电子从金属表面逸出,也就是说金属表面与外界(真空)之间存在一个势垒 1

Eb,因此,电子要从金属中逸出,至少必须具有E的动能。从图2可见,在绝对零度时, 电子逸出金属至少要从外界得到的能量为Eo,即必须克服偶电层的阻力做功V=Eo Eo=Ep-Er=eV (2) Eo(或eV)称为金属电子的逸出功,常用单位为eV,它表征要使处于绝对零度下的金属中 具有最大能量的电子逸出金属表面时,所需要给予的能量,V则称为电子的逸出电势。 (2)热电子发射公式 根据费米一狄拉克能量分布公式,可以推导出热电子发射的理查逊一杜西曼公式 (Richardson-Dushman formula) I=AST2eeVAT (3) 式中,I是热电子发射的电流强度(单位是A):S是阴极金属的有效发射面积(单位是cm): T是热阴极的绝对温度(单位是K):A是与阴极化学纯度有关的系数(单位是A·cm2·K2): k是玻耳兹曼常量,k=1.38×1023J/K 原则上只要测定I,A,S和T,就可以根据式(3)算出阴极的逸出功V。但是困难 在于A和$的测量。所以在实际测量中,通常采用理查逊直线法,借此可以设法避开A和 S的测量。 (3)理查逊直线法 将式(3)两边除以T,再取对数得到 g=1g(AS)-27 =lgAS)-5.04×103V/T (4) 从式(④可以看出,8了与7呈线性关系。蜘以g子和作图。由所得直线的 T 斜率即可求出电子的逸出电势V,这种方法就叫做理查逊直线法。它的优点是可以不必测 的具体数值而直接由I和T就可得到V的值,A和S的影响只是使g为 线平行移动。这种避开不易测量或不易测准的物理量而获得所需结果的方法,在设计方案 中是常用的方法之一。 (4)肖特基(Schottky)效应与外延法求零场电流 式(4)中的1是在阴极与阳极间不存在加速电场情况下的热电子发射电流。但是,为 了维持阴极发射的热电子能连续不断地飞向阳极,必须在阳极和阴极间加一个加速电场E, 由于E的存在会使阴极表面的势垒E降低,因而逸出功减小,发射电流增大,这就是肖特 基效应。可以证明,在加速电场E作用下阴极发射电流L与E有如下的关系 I。=1ea.439VE1m) (5) 式中,I和I分别是加速电场为E和零时的发射电流,对式(5)取对数得 0.439 lgI。=lgI+ 2.30T VE (6) 如果把阴极和阳极做成共轴柱形,并忽略接触电势差和其他影响,则加速电场可表示为 E。= U (7 片xln2
Eb,因此,电子要从金属中逸出,至少必须具有Eb的动能。从图 2 可见,在绝对零度时, 电子逸出金属至少要从外界得到的能量为E0,即必须克服偶电层的阻力做功eV=E0 E0=Eb-EF=eV (2) E0(或eV)称为金属电子的逸出功,常用单位为eV,它表征要使处于绝对零度下的金属中 具有最大能量的电子逸出金属表面时,所需要给予的能量,V则称为电子的逸出电势。 (2) 热电子发射公式 根据费米—狄拉克能量分布公式,可以推导出热电子发射的理查逊—杜西曼公式 (Richardson—Dushman formula) I=AST2 e -eV/kT (3) 式中,I是热电子发射的电流强度(单位是A);S是阴极金属的有效发射面积(单位是cm 2 ); T是热阴极的绝对温度(单位是K);A是与阴极化学纯度有关的系数(单位是A·cm -2·K-2); k是玻耳兹曼常量,k=1.38×10-23J/K. 原则上只要测定 I,A,S 和 T,就可以根据式(3)算出阴极的逸出功 eV。但是困难 在于 A 和 S 的测量。所以在实际测量中,通常采用理查逊直线法,借此可以设法避开 A 和 S 的测量。 (3) 理查逊直线法 将式(3)两边除以T2 ,再取对数得到 AS TV kT eV AS T I /1004.5)lg( 30.2 )lg(lg 3 2 ×−=−= (4) 从式(4)可以看出, 2 lg T I 与 T 1 呈线性关系。如以 2 lg T I 和 T 1 作图,由所得直线的 斜率即可求出电子的逸出电势 V,这种方法就叫做理查逊直线法。它的优点是可以不必测 出 A,S 的具体数值而直接由 I 和 T 就可得到 V 的值,A 和 S 的影响只是使 TT I 1 lg 2 − 直 线平行移动。这种避开不易测量或不易测准的物理量而获得所需结果的方法,在设计方案 中是常用的方法之一。 (4)肖特基(Schottky)效应与外延法求零场电流 式(4)中的I是在阴极与阳极间不存在加速电场情况下的热电子发射电流。但是,为 了维持阴极发射的热电子能连续不断地飞向阳极,必须在阳极和阴极间加一个加速电场Ea, 由于Ea的存在会使阴极表面的势垒Eb降低,因而逸出功减小,发射电流增大,这就是肖特 基效应。可以证明,在加速电场Ea作用下阴极发射电流Ia与Ea有如下的关系 TE )/439.0( a a = IeI (5) 式中,Ia和I分别是加速电场为Ea和零时的发射电流,对式(5)取对数得 a Ea T II 30.2 439.0 lglg += (6) 如果把阴极和阳极做成共轴柱形,并忽略接触电势差和其他影响,则加速电场可表示为 1 2 1 ln r r r U E a a × = (7) 2

式中,r1和r2分别为阴极和阳极的半径,U为加速电压。把式(7)代入式(6)得 lg1。=lgI+ 0.439,0a (8) 2.30T x In 由式(8)可知,在一定温度和管子结构下,lg1。和√可。呈 lgIa 5.10V 0 mP+9 线性关系。如果以√U。为横坐标,以lgI为纵坐标作图,得 1gI 14 T3 T2 直线,如图3所示。此直线的延长线与纵坐标的交点为gI, 由此求出在一定温度下,当加速电场为零时的发射电流I。 T4>T3>…Ti 由上面讨论可知,要测定金属材料的逸出功,首先应该把 图3 被测材料做成二极管阴极,当测定了阴极温度T、阳极电压U和 发射电流Ia后,通过外延法和理查逊直线法即可求出逸出电势和逸出功V (⑤)温度测量与理想的二极管 从热电子发射公式中可以看出,灯丝温度T对发射电流的影响极大,因此准确测量温度 是一个重要问题。一般可用光测高温计通过理想二极管阳极中间的一个小圆孔来测量阴极 的温度,或根据管子的参数及阴极K的加热电流I来计算它的温度。 实验中所用电子管为直流式理想二极管,结构如图4所示,电路如图5所示。二极管的阴 极K由直径0.0075cm左右的钨丝做成。阳极A为长1.5cm,半径r2=0.42cm的镍制圆筒,中间 有一个d=0.15cm的小孔。为了避免灯丝的冷端效应及电场的边缘效应,在阳极两端各有一 圆筒形保护电极B,保护电极与阳极加上同一电势,但其电流并不计入热电子发射电流中, 这种二极管灯丝加热电流1与灯丝的温度T间的对应数值关系由表1给出。 2202 图4 图5 表1理想二极管灯丝电流与温度关系 灯丝电流I(A) 0.50 0.55 0.60 0.65 0.70 0.75 0.80 灯丝温度T(103K) 1.72 1.80 1.88 1.96 2.04 2.12 2.20
式中,r1和r2分别为阴极和阳极的半径,Ua为加速电压。把式(7)代入式(6)得 1 2 1 ln30.2 439.0 lglg r r rT U II a a × += (8) 由式(8)可知,在一定温度和管子结构下, 和a lg I Ua 呈 线性关系。如果以 Ua 为横坐标,以 为纵坐标作图,得一 直线,如图 3 所示。此直线的延长线与纵坐标的交点为 , 由此求出在一定温度下,当加速电场为零时的发射电流 I。 a lg I lg I 由上面讨论可知,要测定金属材料的逸出功,首先应该把 被测材料做成二极管阴极,当测定了阴极温度T、阳极电压Ua和 发射电流Ia后,通过外延法和理查逊直线法即可求出逸出电势和逸出功eV (5) 温度测量与理想的二极管 从热电子发射公式中可以看出,灯丝温度T对发射电流的影响极大,因此准确测量温度 是一个重要问题。一般可用光测高温计通过理想二极管阳极中间的一个小圆孔来测量阴极 的温度,或根据管子的参数及阴极K的加热电流If来计算它的温度。 实验中所用电子管为直流式理想二极管,结构如图 4 所示,电路如图 5 所示。二极管的阴 极K由直径 0.0075cm左右的钨丝做成。阳极A为长 1.5cm,半径r2=0.42cm的镍制圆筒,中间 有一个d=0.15cm的小孔。为了避免灯丝的冷端效应及电场的边缘效应,在阳极两端各有一 圆筒形保护电极B,保护电极与阳极加上同一电势,但其电流并不计入热电子发射电流中, 这种二极管灯丝加热电流If与灯丝的温度T间的对应数值关系由表 1 给出。 表 1 理想二极管灯丝电流与温度关系 灯丝电流If(A) 0.50 0.55 0.60 0.65 0.70 0.75 0.80 灯丝温度T(103 K) 1.72 1.80 1.88 1.96 2.04 2.12 2.20 220Ω×2 5 1 2 6 3 4 Uf A V A Ua μ 图 5 K B A B 图 4 5 10 lgIa lgI T4 T3 T2 T1 O Ua T4>T3>…T1 图 3 3

(6)实验电路 根据实验原理实验电路如图5所示 【实验内容】 1.熟悉仪器装置,并连接好安培表(1安培,测量灯丝电流),和微安表(1000微安, 测量阳极电流缸)。伏特表己安装在逸出功测定仪上)接通电源,预热10分钟。 2.取理想二极管灯丝电流1从0.55~0.75安培,每间隔0.05安培进行一次测量。对应 每一灯丝电流,在阳极上加25、36、49、64、…144伏特诸电压,各测出一组阳极电流 1a。记录数据于表一,并换算至表二。 3.根据表二数据,做出gI。~√U。图线。求出截距,即可得到在不同阴极温度时的零 场热电子发射电流I,并换算成表三。 11 4根据表三数据,做出g广~7图线。从直线斜率求出钨的逸出功V或逸出电势 V。 5.分析讨论本实验产生测量误差的原因。 【数据表格】 表一 I.(106A)aV) 25 36 49 64 81 100 121 144 L(A) 0.75 0.70 0.65 0.60 0.55 表二 Lgla U.) 5.0 6.0 7.0 8.0 9.0 10.0 11.0 12.0 T(10R
(6)实验电路 根据实验原理实验电路如图 5 所示 【实验内容】 1. 熟悉仪器装置,并连接好安培表(1 安培,测量灯丝电流If),和微安表(1000 微安, 测量阳极电流Ia)。伏特表已安装在逸出功测定仪上)接通电源,预热 10 分钟。 2. 取理想二极管灯丝电流If从 0.55~0.75 安培,每间隔 0.05 安培进行一次测量。对应 每一灯丝电流,在阳极上加 25、36、49、64、……144 伏特诸电压,各测出一组阳极电流 Ia.。记录数据于表一,并换算至表二。 3.根据表二数据,做出 ~a lg I Ua 图线。求出截距,即可得到在不同阴极温度时的零 场热电子发射电流 I,并换算成表三。 4. 根据表三数据,做出 2 1 lg T ~ T 1 图线。从直线斜率求出钨的逸出功 eV 或逸出电势 V。 5. 分析讨论本实验产生测量误差的原因。 【数据表格】 表一 25 36 49 64 81 100 121 144 0.75 0.70 0.65 0.60 0.55 表二 5.0 6.0 7.0 8.0 9.0 10.0 11.0 12.0 Ia(10-6A) Ua(V) If(A) LgIa VU )( a T(10K) 4
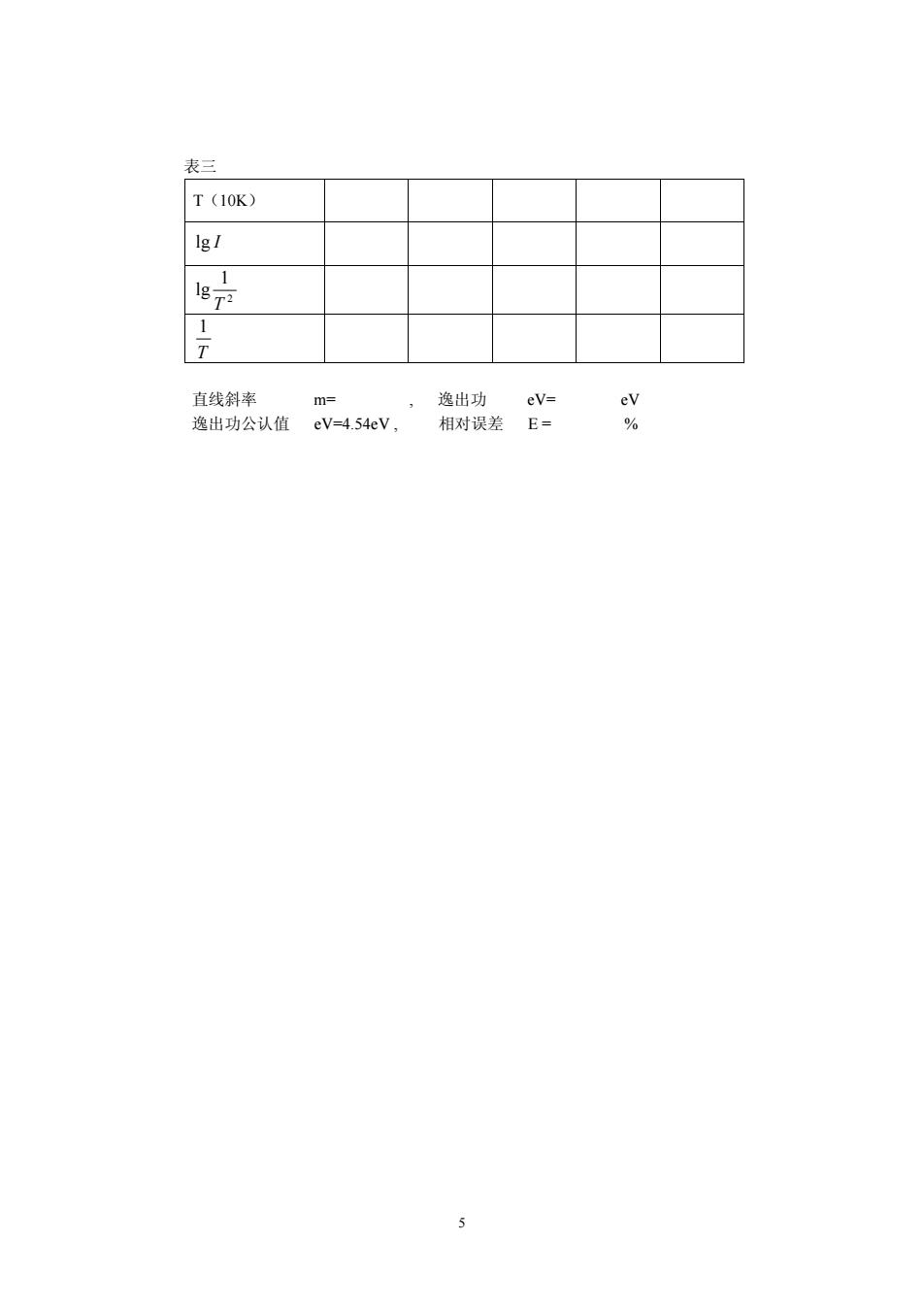
表三 T(10K) IgI 1 g 直线斜率 m= 逸出功 eV= ev 逸出功公认值 eV=4.54eV. 相对误差 E= % 5
表三 T(10K) lg I 2 1 lg T T 1 直线斜率 m= , 逸出功 eV= eV 逸出功公认值 eV=4.54eV , 相对误差 E = % 5