
实验十二 用快速电子验证相对论效应 相对论是现代物理学的重要基石.它的建立是20世纪自然科学最伟大的发现之一,对 物理学乃至哲学思想都有深远影响.本实验利用半圆聚焦B磁谱仪,通过测定快速电子的 动量值和动能值,来验证动量和动能之间的相对论关系 【实验目的】 1.学习相对论动量和动能的一些基本原理: 2.了解B磁谱仪测量原理,掌握能谱测量方法: 3.通过对快速电子的动量值及和动能值的测定,验证动量和动能之间的相对论关系, 【实验原理】 1.相对论效应 经典力学把时间和空间看作是彼此无关的,把时间和空间的基本属性也看作与物质的 运动没有任何关系而是绝对的、永远不变的.这就是所谓经典力学中的“绝对时间”和“绝 对空间”的观点,也称作牛顿绝对时空观.但是,随着物理学的发展,特别是20世纪初叶 就已发现一些现象与经典力学的一些概念和定律相抵触,牛顿的绝对时空观和建立在这一 基础上的经典力学开始陷入了无法解决的困境. 在这种情况下,1905年爱因斯坦提出了狭义相对论.这一理论描述了一种新的时空观, 认为时间和空间是相互联系的,而且时间的流逝和空间的延拓也与物质和运动有不可分割 的联系.按照爱因斯坦的狭义相对论,在洛伦兹变换下,静止质量为mo、速度为的质点, 其动量应为 p= mo y=mv (1) V1-B2 式中m=m,/1-B2,B=v1c.相对论的能量E为 E=me2 (2) 这就是著名的质能关系.mc是运动物体的总能量,物体静止时的能量E。=moc2称为静止 能量,两者之差为物体的动能Ek,即 E mc2 -moc2 =mo (3) 1-B 当B<1时,式(3)可展开为 -61-
实验十二 用快速电子验证相对论效应 相对论是现代物理学的重要基石.它的建立是 20 世纪自然科学最伟大的发现之一,对 物理学乃至哲学思想都有深远影响.本实验利用半圆聚焦β 磁谱仪,通过测定快速电子的 动量值和动能值,来验证动量和动能之间的相对论关系. 【实验目的】 1.学习相对论动量和动能的一些基本原理; 2.了解β 磁谱仪测量原理,掌握能谱测量方法; 3.通过对快速电子的动量值及和动能值的测定,验证动量和动能之间的相对论关系. 【实验原理】 1.相对论效应 经典力学把时间和空间看作是彼此无关的,把时间和空间的基本属性也看作与物质的 运动没有任何关系而是绝对的、永远不变的.这就是所谓经典力学中的“绝对时间”和“绝 对空间”的观点,也称作牛顿绝对时空观.但是,随着物理学的发展,特别是 20 世纪初叶 就已发现一些现象与经典力学的一些概念和定律相抵触,牛顿的绝对时空观和建立在这一 基础上的经典力学开始陷入了无法解决的困境. 在这种情况下,1905 年爱因斯坦提出了狭义相对论.这一理论描述了一种新的时空观, 认为时间和空间是相互联系的,而且时间的流逝和空间的延拓也与物质和运动有不可分割 的联系.按照爱因斯坦的狭义相对论,在洛伦兹变换下,静止质量为m0、速度为v的质点, 其动量应为 mvv m p = − = 2 0 1 β (1) 式中 2 mm 0 1/ −= β , β = / cv .相对论的能量 E 为 2 = mcE (2) 这就是著名的质能关系.mc 2 是运动物体的总能量,物体静止时的能量 称为静止 能量,两者之差为物体的动能E 2 00 = cmE k,即 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − =−= 1 1 1 2 2 0 2 0 2 β k cmcmmcE (3) 当β <<1 时,式(3)可展开为 - 61 -
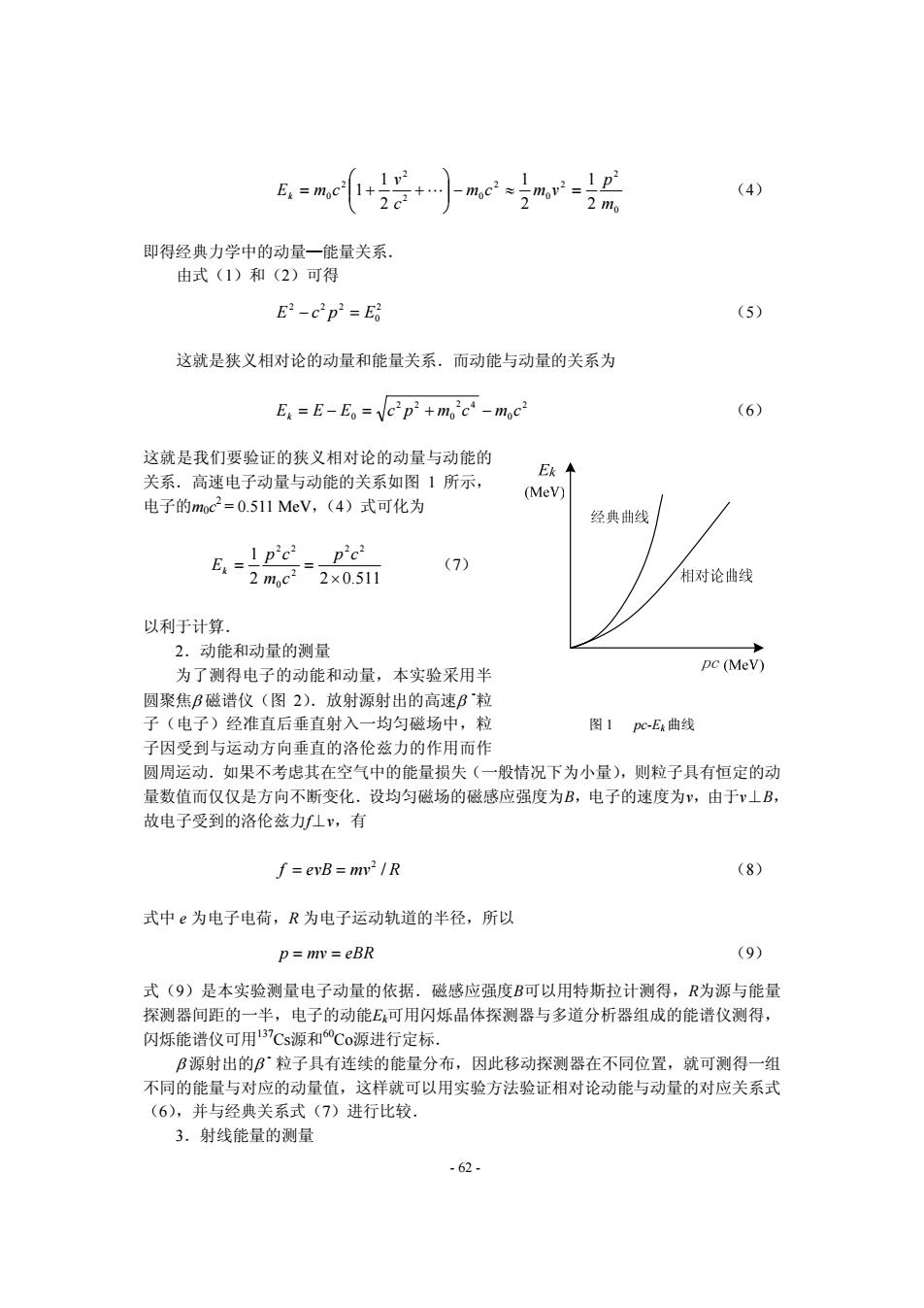
Eg=moci 2c+-mcp 1v2, (4) 2 2 mo 即得经典力学中的动量一能量关系. 由式(1)和(2)可得 E2-c2p2=E昭 (5) 这就是狭义相对论的动量和能量关系.而动能与动量的关系为 E=E-E。=VCp2+m,c-mc2 (6) 这就是我们要验证的狭义相对论的动量与动能的 Ek个 关系.高速电子动量与动能的关系如图1所示, (MeV) 电子的moc2=0.511MeV,(4)式可化为 经典曲线 =Ip'c: _p'c2 2m,c2-2×0.51m (7) 相对论曲线 以利于计算. 2.动能和动量的测量 为了测得电子的动能和动量,本实验采用半 pC(Mev) 圆聚焦B磁谱仪(图2).放射源射出的高速Bˉ粒 子(电子)经准直后垂直射入一均匀磁场中,粒 图1pc-Ek曲线 子因受到与运动方向垂直的洛伦兹力的作用而作 圆周运动.如果不考虑其在空气中的能量损失(一般情况下为小量),则粒子具有恒定的动 量数值而仅仅是方向不断变化.设均匀磁场的磁感应强度为B,电子的速度为v,由于ⅴ⊥B, 故电子受到的洛伦兹力fL",有 f=evB=mv2/R (8) 式中e为电子电荷,R为电子运动轨道的半径,所以 p=my=eBR (9) 式(9)是本实验测量电子动量的依据,.磁感应强度B可以用特斯拉计测得,R为源与能量 探测器间距的一半,电子的动能E可用闪烁晶体探测器与多道分析器组成的能谱仪测得, 闪烁能谱仪可用137Cs源和℃o源进行定标. B源射出的B~粒子具有连续的能量分布,因此移动探测器在不同位置,就可测得一组 不同的能量与对应的动量值,这样就可以用实验方法验证相对论动能与动量的对应关系式 (6),并与经典关系式(7)进行比较. 3.射线能量的测量 -62-
0 2 2 0 2 2 0 2 2 0 2 1 2 1 2 1 1 m p vmcm c v k cmE =≈−⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ++= " (4) 即得经典力学中的动量—能量关系. 由式(1)和(2)可得 2 0 222 =− EpcE (5) 这就是狭义相对论的动量和能量关系.而动能与动量的关系为 2 0 2 4 0 22 0 k −+=−= cmcmpcEEE (6) 这就是我们要验证的狭义相对论的动量与动能的 关系.高速电子动量与动能的关系如图 1 所示, 电子的m0c 2 = 0.511 MeV,(4)式可化为 511.022 1 22 2 0 22 × == cp cm cp Ek (7) 以利于计算. 2.动能和动量的测量 为了测得电子的动能和动量,本实验采用半 圆聚焦β 磁谱仪(图 2).放射源射出的高速β -粒 子(电子)经准直后垂直射入一均匀磁场中,粒 子因受到与运动方向垂直的洛伦兹力的作用而作 圆周运动.如果不考虑其在空气中的能量损失(一般情况下为小量),则粒子具有恒定的动 量数值而仅仅是方向不断变化.设均匀磁场的磁感应强度为B,电子的速度为v,由于v⊥B, 故电子受到的洛伦兹力f⊥v,有 图 1 pc-Ek 曲线 == 2 / RmvevBf (8) 式中 e 为电子电荷,R 为电子运动轨道的半径,所以 == eBRmvp (9) 式(9)是本实验测量电子动量的依据.磁感应强度B可以用特斯拉计测得,R为源与能量 探测器间距的一半,电子的动能Ek可用闪烁晶体探测器与多道分析器组成的能谱仪测得, 闪烁能谱仪可用137Cs源和60Co源进行定标. β 源射出的β - 粒子具有连续的能量分布,因此移动探测器在不同位置,就可测得一组 不同的能量与对应的动量值,这样就可以用实验方法验证相对论动能与动量的对应关系式 (6),并与经典关系式(7)进行比较. 3.射线能量的测量 - 62 -
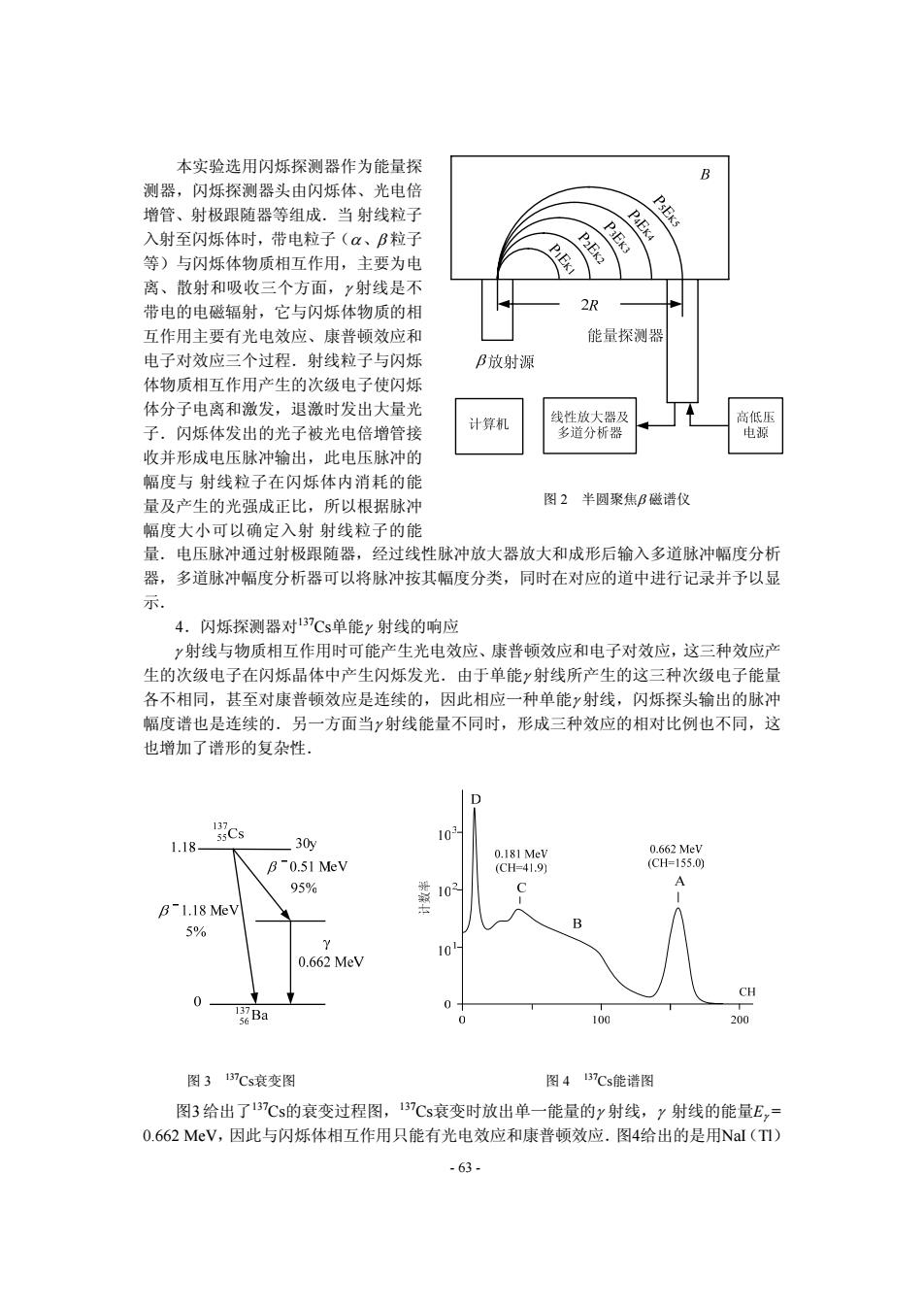
本实验选用闪烁探测器作为能量探 测器,闪烁探测器头由闪烁体、光电倍 增管、射极跟随器等组成.当射线粒子 PsEks 入射至闪烁体时,带电粒子(、B粒子 P4EK4 等)与闪烁体物质相互作用,主要为电 P2EK2 离、散射和吸收三个方面,y射线是不 带电的电磁辐射,它与闪烁体物质的相 2R 互作用主要有光电效应、康普顿效应和 能量探测器 电子对效应三个过程.射线粒子与闪烁 B放射源 体物质相互作用产生的次级电子使闪烁 体分子电离和激发,退激时发出大量光 线性放大器及 高低压 子.闪烁体发出的光子被光电倍增管接 计算机 多道分析器 电源 收并形成电压脉冲输出,此电压脉冲的 幅度与射线粒子在闪烁体内消耗的能 量及产生的光强成正比,所以根据脉冲 图2半圆聚焦B磁谱仪 幅度大小可以确定入射射线粒子的能 量.电压脉冲通过射极跟随器,经过线性脉冲放大器放大和成形后输入多道脉冲幅度分析 器,多道脉冲幅度分析器可以将脉冲按其幅度分类,同时在对应的道中进行记录并予以显 示. 4.闪烁探测器对137℃s单能y射线的响应 y射线与物质相互作用时可能产生光电效应、康普顿效应和电子对效应,这三种效应产 生的次级电子在闪烁晶体中产生闪烁发光.由于单能y射线所产生的这三种次级电子能量 各不相同,甚至对康普顿效应是连续的,因此相应一种单能y射线,闪烁探头输出的脉冲 幅度谱也是连续的.另一方面当y射线能量不同时,形成三种效应的相对比例也不同,这 也增加了谱形的复杂性 D Cs 1.18- 30y 103 0.181 Mev 0.662MeV B0.51 MeV (CH=41.9) (CH=155.0) 95% C A B-1.18 Mev 5% B Y 101 0.662MeV CH 0 a 0 0 100 200 图3137Cs衰变图 图413Cs能谱图 图3给出了13Cs的衰变过程图,137Cs衰变时放出单一能量的y射线,y射线的能量E,= 0.662MV,因此与闪烁体相互作用只能有光电效应和康普顿效应.图4给出的是用Nal(T1) -63-
本实验选用闪烁探测器作为能量探 测器,闪烁探测器头由闪烁体、光电倍 增管、射极跟随器等组成.当 射线粒子 入射至闪烁体时,带电粒子(α、β 粒子 等)与闪烁体物质相互作用,主要为电 离、散射和吸收三个方面,γ 射线是不 带电的电磁辐射,它与闪烁体物质的相 互作用主要有光电效应、康普顿效应和 电子对效应三个过程.射线粒子与闪烁 体物质相互作用产生的次级电子使闪烁 体分子电离和激发,退激时发出大量光 子.闪烁体发出的光子被光电倍增管接 收并形成电压脉冲输出,此电压脉冲的 幅度与 射线粒子在闪烁体内消耗的能 量及产生的光强成正比,所以根据脉冲 幅度大小可以确定入射 射线粒子的能 量.电压脉冲通过射极跟随器,经过线性脉冲放大器放大和成形后输入多道脉冲幅度分析 器,多道脉冲幅度分析器可以将脉冲按其幅度分类,同时在对应的道中进行记录并予以显 示. 5 K5 4 K4 3 K3 2 K2 1 K1 图 2 半圆聚焦β 磁谱仪 4.闪烁探测器对137Cs单能γ 射线的响应 γ 射线与物质相互作用时可能产生光电效应、康普顿效应和电子对效应,这三种效应产 生的次级电子在闪烁晶体中产生闪烁发光.由于单能γ 射线所产生的这三种次级电子能量 各不相同,甚至对康普顿效应是连续的,因此相应一种单能γ 射线,闪烁探头输出的脉冲 幅度谱也是连续的.另一方面当γ 射线能量不同时,形成三种效应的相对比例也不同,这 也增加了谱形的复杂性. 图3 给出了137Cs的衰变过程图,137Cs衰变时放出单一能量的γ 射线,γ 射线的能量Eγ = 0.662 MeV,因此与闪烁体相互作用只能有光电效应和康普顿效应.图4给出的是用NaI(Tl) 图 3 137Cs衰变图 图 4 137Cs能谱图 - 63 -

闪烁探测器测得的13Cs能谱,谱中有三个峰和一个平台.在光电效应过程中,入射的y光 子把能量全部转移给原子中的束缚电子,使之发射出来,而光子本身消失.图4中的A峰称 为全能峰或光电峰,它主要是由光电效应产生的.在康普顿效应中散射电子的能量在0~ 0.477MV范围内,产生宽的康普顿平台,见图4B处.康普顿平台上的C峰称为反散射峰(能 量为0.181MeV),D峰是X射线峰(能量约32KeV). 【实验仪器】 实验仪器框图见图2. 1.放射源 在选用B放射源时,应考虑 放射源的Bˉ射线最大能量Emax Co 2.81 5.27y 要大,其Bˉ粒子速度越接近光 B 0.32 MeV 100% 速则越能明显地反映出相对论 与经典力学的差异.另外,该放 y 1.17 MeV 射源的半衰期要尽可能的长,以 便于多年长期使用.本实验选用 Egmax y 1.33 MeV 8Sr-9YB放射源,其B能谱 En(MeV N 图见图5,其中Emax(Sr)=0.546 MeV,Eemax (Y)=2.27 MeV. 图5 8Sr-9y能谱图 图660℃0衰变图 放射源做成点源,强度约为1 Ci,外壳由铅铝组合做成圆柱形防护壳,以达到安全防护的要求, 本实验采用37Cs和C0y源对闪烁能谱仪进行能量定标,1B7Csy能谱的光电峰(或全 能峰)对应的能量为0.662MV.图6给出了Co的衰变图,它的两个光电峰对应的能量分 别为1.17MeV和1.33MeV.y源强度约为1.5uCi,也采用铝和铅进行屏蔽 2.探测器 由于Nl(TI)晶体易潮解,因此用铝膜密封并遮挡杂散光.铝膜前面是一条供B粒 子入射的狭缝,B粒子通过铝膜时,有少量能量损失,需进行修正.为了降低本底的影响, Nal(T1)晶体外壳采用了铅铝组合屏蔽措施. 由于光电倍增管是一个电子光学系统,如果太靠近磁场,电子光学系统将受边缘磁场 的影响而不能正常工作.为此在闪烁晶体与光电倍增管之间加了一个25mm长的光导管, 以使光电倍增管的光电阴极远离边缘磁场,并且在光电倍增管外包以非晶态合金薄膜进行 磁屏蔽 3.磁场 本实验装置的均匀磁场空间范围为325mm×170mm×32mm,采用铁氧永磁材料Y25-F 做成,整个磁板由小磁铁棒拼接而成,再整体充磁.为了提高磁场均匀性,两对板上贴上 了薄铁板.本装置的平均磁感应强度约为75mT. 【实验内容】 1.闪烁能谱仪的能量定标 -64-
闪烁探测器测得的137Cs能谱,谱中有三个峰和一个平台.在光电效应过程中,入射的γ 光 子把能量全部转移给原子中的束缚电子,使之发射出来,而光子本身消失.图4中的A峰称 为全能峰或光电峰,它主要是由光电效应产生的.在康普顿效应中散射电子的能量在0~ 0.477 MeV范围内,产生宽的康普顿平台,见图4B处.康普顿平台上的C 峰称为反散射峰(能 量为0.181 MeV),D峰是X射线峰(能量约32 KeV). 【实验仪器】 实验仪器框图见图 2. 1.放射源 在选用β 放射源时,应考虑 放射源的β - 射线最大能量Eβmax 要大,其β - 粒子速度越接近光 速则越能明显地反映出相对论 与经典力学的差异.另外,该放 射源的半衰期要尽可能的长,以 便于多年长期使用.本实验选用 β 放射源,其β 能谱 图见图 5,其中E YSr 90 39 90 38 − βmax(Sr)= 0.546 MeV,Eβmax(Y)= 2.27 MeV.本 放射源做成点源,强度约为 1 mCi,外壳由铅铝组合做成圆柱形防护壳,以达到安全防护的要求. 2.81 0 5.27y Co Ni 60 27 60 28 - eV 100% eV eV 图 5 YSr 能谱图 图 6 90 39 90 38 − 60Co衰变图 本实验采用137Cs和60Co γ 源对闪烁能谱仪进行能量定标,137Cs γ 能谱的光电峰(或全 能峰)对应的能量为 0.662 MeV.图 6 给出了60Co的衰变图,它的两个光电峰对应的能量分 别为 1.17 MeV和 1.33 MeV. γ 源强度约为 1.5 μCi,也采用铝和铅进行屏蔽. 2.探测器 由于NaI(Tl)晶体易潮解,因此用铝膜密封并遮挡杂散光.铝膜前面是一条供β- 粒 子入射的狭缝,β - 粒子通过铝膜时,有少量能量损失,需进行修正.为了降低本底的影响, NaI(Tl)晶体外壳采用了铅铝组合屏蔽措施. 由于光电倍增管是一个电子光学系统,如果太靠近磁场,电子光学系统将受边缘磁场 的影响而不能正常工作.为此在闪烁晶体与光电倍增管之间加了一个 25 mm 长的光导管, 以使光电倍增管的光电阴极远离边缘磁场,并且在光电倍增管外包以非晶态合金薄膜进行 磁屏蔽. 3.磁场 本实验装置的均匀磁场空间范围为 325 mm×170 mm×32 mm,采用铁氧永磁材料 Y25-F 做成,整个磁板由小磁铁棒拼接而成,再整体充磁.为了提高磁场均匀性,两对板上贴上 了薄铁板.本装置的平均磁感应强度约为 75 mT. 【实验内容】 1.闪烁能谱仪的能量定标 - 64 -

调整加到闪烁探测器上的高压,选择合适的放大倍数,分别测量3℃s和C0的y能谱, 并从中确定Co两个光电峰(对应能量1.17MeV和1.33MeV)峰位的道数,以及137Cs反散 射峰(对应能量0.184MeV)和光电峰(对应能量0.662MeV)峰位的道数.根据各峰位的 道数和分别对应的能量,用最小二乘法拟合来定标谱仪,求出道位与能量的对应关系. 提示:选择放大倍数,应保证测量高能B粒子(1.8~1.9MeV)时不超出多道分析器 的量程范围,又能充分利用多道的有效测量范围. 2.B粒子动能及动量的测量 打开机械泵抽真空,机械泵正常运转2~3分钟即可停止工作.对不同的电子偏转半径, 分别测量B能谱,并求出各个B能谱的峰位道数,根据能量定标结果,由道数求得各个峰位 对应的能量. 提示:测量时探测器与B源的距离△X最近要小于9cm,最远要大于24cm,以保证获 得动能范围0.41.8MeV的电子. 3.实验数据的处理 (1)根据能量定标数据求定标曲线 己知一组能量定标数据(E,CH,),根据最小二乘法原理,用线性拟合的方法即可求 得能量E和道数CH之间的关系 E=a+bxCH (2)B粒子动能的计算 由于B粒子与物质的相互作用,因此对其损失的能量进行必要的修正十分重要. ①Bˉ粒子在铝膜中的能量损失修正 在计算Bˉ粒子的动能时,需要对粒子穿过铝膜(220um:200um为Nal(TI)晶体的 铝膜密封层厚度,20为反射层的铝膜厚度)时的动能予以修正.设Bˉ粒子在铝膜中穿 越△x的动能损失为△E,则 AE=dE P△x (10) dxo 其中近(dE<0)是铝对B粒子的能量吸收系数,P是铝的密度,5是关于B的函数。 dxpdxp dxp 不同E情况下dE的取值可以通过计算得到.设E=K(E),则△E=K(EAx,取 dxp dxp △x→0,则B~粒子穿过整个铝膜的能量损失为 E-E =K(E)dx (11) 即 E=E:-K(EXix (12) 其中d为薄膜的厚度,E,为出射后的动能,E,为入射前的动能.由于实验探测到的是经铝膜 衰减后的动能,所以经公式(12)可计算出入射前的动能.计算可采用梯形积分法在计算 -65-
调整加到闪烁探测器上的高压,选择合适的放大倍数,分别测量137Cs和60Co的γ 能谱, 并从中确定60Co两个光电峰(对应能量 1.17 MeV和 1.33 MeV)峰位的道数,以及137Cs反散 射峰(对应能量 0.184 MeV)和光电峰(对应能量 0.662 MeV)峰位的道数.根据各峰位的 道数和分别对应的能量,用最小二乘法拟合来定标谱仪,求出道位与能量的对应关系. 提示:选择放大倍数,应保证测量高能β -粒子(1.8~1.9 MeV)时不超出多道分析器 的量程范围,又能充分利用多道的有效测量范围. 2.β - 粒子动能及动量的测量 打开机械泵抽真空,机械泵正常运转 2~3 分钟即可停止工作.对不同的电子偏转半径, 分别测量β 能谱,并求出各个β 能谱的峰位道数,根据能量定标结果,由道数求得各个峰位 对应的能量. 提示:测量时探测器与β 源的距离ΔX 最近要小于 9 cm,最远要大于 24 cm,以保证获 得动能范围 0.4~1.8 MeV 的电子. 3.实验数据的处理 (1)根据能量定标数据求定标曲线 已知一组能量定标数据(Ei,CHi),根据最小二乘法原理,用线性拟合的方法即可求 得能量E和道数CH之间的关系 ×+= CHbaE (2)β - 粒子动能的计算 由于β 粒子与物质的相互作用,因此对其损失的能量进行必要的修正十分重要. ①β - 粒子在铝膜中的能量损失修正 在计算β - 粒子的动能时,需要对粒子穿过铝膜(220 μm:200 μm为NaI(Tl)晶体的 铝膜密封层厚度,20 μm为反射层的铝膜厚度)时的动能予以修正.设β - 粒子在铝膜中穿 越Δx的动能损失为ΔE,则 x x E E ρ Δ=Δ d ρ d (10) 其中 xρ E d d ( xρ E d d <0)是铝对β 粒子的能量吸收系数,ρ 是铝的密度, xρ E d d 是关于E的函数, 不同E情况下 xρ E d d 的取值可以通过计算得到.设 )( d d EK x E = ρ ,则 Δ )( Δ= xEKE ,取 x →Δ 0,则β - 粒子穿过整个铝膜的能量损失为 ( ) ∫ + =− dx x 12 dxEKEE (11) 即 ( ) ∫ + −= dx x 21 dxEKEE (12) 其中d为薄膜的厚度,E2为出射后的动能,E1为入射前的动能.由于实验探测到的是经铝膜 衰减后的动能,所以经公式(12)可计算出入射前的动能.计算可采用梯形积分法在计算 - 65 -

机上完成,表1为计算结果。 表1入射动能E和出射动能E之间的对应关系 E (MeV) E2 (MeV) E (MeV) E2 (MeV) E (MeV) E2 (MeV) 0.317 0.200 0.887 0.800 1.489 1.400 0.360 0.250 0.937 0.850 1.536 1.450 0.404 0.300 0.988 0.900 1.583 1.500 0.451 0.350 1.039 0.950 1.638 1.550 0.497 0.400 1.090 1.000 1.685 1.600 0.545 0.450 1.137 1.050 1.740 1.650 0.595 0.500 1.184 1.100 1.787 1.700 0.640 0.550 1.239 1.150 1.834 1.750 0.690 0.600 1.286 1.200 1.889 1.800 0.740 0.650 1.333 1.250 1.936 1.850 0.790 0.700 1.388 1.300 1.991 1.900 0.840 0.750 1.435 1.350 2.038 1.950 ②B~粒子在有机塑料薄膜中的能量损失修正 实验表明封装真空室的有机塑料薄膜对Bˉ存在一定的能量吸收,尤其对小于0.4MV 的B粒子吸收近0.02MV.由于塑料薄膜的厚度及物质组分难以测量,可采用实验的方法 进行修正,实验测量了不同能量下入射动能E和出射动能E的关系(表2),采用分段插值 的方法即可计算修正值, 表2入射动能E和出射动能E的关系 Ek (MeV) 0.382 0.581 0.777 0.973 1.173 1.367 1.567 1.752 Eo (MeV) 0.365 0.571 0.770 0.966 1.166 1.360 1.557 1.747 实验中可以根据表1和表2,利用线性插值对Bˉ粒子作能量损失修正. (3)B粒子动量的计算 各个测量位置上对应的动量p值可由 (9)式算得. 由于磁场的非均匀性(尤其是边缘部 分)无法避免,直接用式(9)求动量将产 生一定的系统误差,因此需要采用更为合理 的方式来表述p与4X的关系, 如图6所示,设粒子的真实径迹为aob, 0 X a △X 位移ds与Y的夹角为0,则d在X轴上的 投影为sin0·d,显然有 图6粒子在磁场中的径迹 △r=sin0-dk≈0sin0dk6a,≈z) (13) -66-
机上完成,表 1 为计算结果. 表 1 入射动能E1和出射动能E2之间的对应关系 E1(MeV) E2(MeV) E1(MeV) E2(MeV) E1(MeV) E2(MeV) 0.317 0.200 0.887 0.800 1.489 1.400 0.360 0.250 0.937 0.850 1.536 1.450 0.404 0.300 0.988 0.900 1.583 1.500 0.451 0.350 1.039 0.950 1.638 1.550 0.497 0.400 1.090 1.000 1.685 1.600 0.545 0.450 1.137 1.050 1.740 1.650 0.595 0.500 1.184 1.100 1.787 1.700 0.640 0.550 1.239 1.150 1.834 1.750 0.690 0.600 1.286 1.200 1.889 1.800 0.740 0.650 1.333 1.250 1.936 1.850 0.790 0.700 1.388 1.300 1.991 1.900 0.840 0.750 1.435 1.350 2.038 1.950 ②β - 粒子在有机塑料薄膜中的能量损失修正 实验表明封装真空室的有机塑料薄膜对β - 存在一定的能量吸收,尤其对小于 0.4 MeV 的β - 粒子吸收近 0.02 MeV.由于塑料薄膜的厚度及物质组分难以测量,可采用实验的方法 进行修正.实验测量了不同能量下入射动能Ek和出射动能E0的关系(表 2),采用分段插值 的方法即可计算修正值. 表 2 入射动能Ek和出射动能E0的关系 Ek(MeV) 0.382 0.581 0.777 0.973 1.173 1.367 1.567 1.752 E0(MeV) 0.365 0.571 0.770 0.966 1.166 1.360 1.557 1.747 实验中可以根据表 1 和表 2,利用线性插值对β - 粒子作能量损失修正. (3)β - 粒子动量的计算 各个测量位置上对应的动量 p 值可由 (9)式算得. 0 X ds Y a b o ΔX θ 图 6 粒子在磁场中的径迹 由于磁场的非均匀性(尤其是边缘部 分)无法避免,直接用式(9)求动量将产 生一定的系统误差,因此需要采用更为合理 的方式来表述 p 与ΔX 的关系. 如图 6 所示,设粒子的真实径迹为 aob, 位移 ds 与 Y 的夹角为θ,则 ds 在 X 轴上的 投影为sinθ ⋅ ds ,显然有 X ds ⋅≈⋅=Δ ds ∫∫θ π θ θ 0 0 sin sin 1 ( θ ≈ π ) ∵ 1 (13) - 66 -

又因为及R=p/eB,其中R和B分别为ds处的曲率半径和磁感应强度,则有 A=如8Bd0=工09a0(:真空中p为定值 (14) e Jo B 所以有 d0) (15) B 若把言改写成0日0/s血6,0,则物理含义更为明显,即 为粒子在整个路径上 B B 的磁感应强度的倒数以所处位置处的位移与Y轴夹角的正弦为权重的加权平均值.显然, B相当于均匀磁场情形下p=eBR=eBAX/2中的磁感应强度B,即求出B就能更为确切 地表述p与4X的关系,进而准确地确定粒子的动量值. 4.根据B粒子的动能,由动能和动量的相对论关系(6)式求出动量c(为与动能量 纲统一,故把动量p乘以光速,这样两者单位均为MeV)的理论值.在pc(MeV)-Ek(MeV) 坐标系中作实验曲线和相对论关系理论曲线,并与根据(7)式求出的动量℃所作经典理论 曲线比较.求出实验点的动量c与相对论关系理论值的相对误差. 【注意事项】 1.若要打开机玻璃防护罩,应先关闭B源. 2.防止B源强烈振动,以免损坏其密封薄膜. 3.开机预热20分钟后,方能进行测量. 4.实验完毕后,请关闭各放射源. 【思考题】 1.测量能谱进行能量定标时,全能峰所对应的脉冲幅度应选择多大? 2.试比较c-E坐标系中的实验曲线和理论曲线,并进行讨论和得出结论. 3.用y放射源对闪烁探测器进行能量定标时,为什么不需要对y射线穿过220厚的铝 膜进行能量损失的修正? 【参考文献】 []陈玲燕等.相对论效应实验及装置.物理实验,1987 [2]复日大学等合编。原子核物理实验方法.原子能出版社,1986 -67-
又因为及 ,其中 = / eBpR R 和 B 分别为 ds 处的曲率半径和磁感应强度,则有 θ θ θθ π π d Be p d eB p X =⋅⋅=Δ ⋅ ∫0 ∫0 sin sin (∵真空中 p 为定值) (14) 所以有 XeB B Δ= Xep Δ= ∫ 2 1 d sin 0 π θ ϑ (其中 θ π θ d B sim B = ⋅ ∫0 2 11 ) (15) 若把 B 1 改写成 θθθ π θ π d d B ⋅ ⋅ 0 ∫∫ 0 sin/ sin ,则物理含义更为明显,即 B 1 为粒子在整个路径上 的磁感应强度的倒数以所处位置处的位移与 Y 轴夹角的正弦为权重的加权平均值.显然, B 相当于均匀磁场情形下 = = ΔXeBeBRp 2/ 中的磁感应强度 B,即求出 B 就能更为确切 地表述 p 与ΔX 的关系,进而准确地确定粒子的动量值. 4.根据β- 粒子的动能,由动能和动量的相对论关系(6)式求出动量pc(为与动能量 纲统一,故把动量p乘以光速,这样两者单位均为MeV)的理论值.在pc(MeV)-Ek (MeV) 坐标系中作实验曲线和相对论关系理论曲线,并与根据(7)式求出的动量pc所作经典理论 曲线比较.求出实验点的动量pc与相对论关系理论值的相对误差. 【注意事项】 1.若要打开机玻璃防护罩,应先关闭β 源. 2.防止β 源强烈振动,以免损坏其密封薄膜. 3.开机预热20分钟后,方能进行测量. 4.实验完毕后,请关闭各放射源. 【思考题】 1.测量γ能谱进行能量定标时,全能峰所对应的脉冲幅度应选择多大? 2.试比较pc-Ek坐标系中的实验曲线和理论曲线,并进行讨论和得出结论. 3.用γ 放射源对闪烁探测器进行能量定标时,为什么不需要对γ 射线穿过 220 厚的铝 膜进行能量损失的修正? 【参考文献】 [1] 陈玲燕等.相对论效应实验及装置.物理实验,1987 [2] 复旦大学等合编.原子核物理实验方法.原子能出版社,1986 - 67 -