
信号傅立叶分析项目 基本原理 在科学技术的各个领域,存在各种复杂的信号。不管信号多复杂都可以分解为不同频率 的正弦分量。频谱函数描述了信号含有的正弦分量的频率和振幅的关系,是信号最基本的特 征之一。信号的傅立叶分析就是计算信号的频谱函数。 周期函数的频谱函数 周期为T的周期信号可以展开成傅立叶级数: fd+a.cos(xnv,+b,sin(xnv] =C(0)+∑C,[cos(2πnv,)+(n 式中:C0=V匠+6p)=g(守 分别是n次谐波的振幅和相位。把才C(n)看作是n或2πnv。的函数,称为振幅频谱。 中(n)看作是是n或2πnv的函数,称为相位频谱。一般情况下只要知道振幅频谱就够 了,因而通常所称的频谱是指振幅频谱。 非周期函数的频谱函数 非周期函数可以看作是周期函数当周期趋向于∞时的极限情况。只要将周期函数的傅 立叶级数改写成傅立叶积分即可得相似的结果。 二.实验内容及要求 1.利用软件,给出信号发生器的周期信号(方波,正弦波,之字形波)图及对应傅立叶谱 图,根据傅立叶谱找出信号的中心频率。 2.利用软件,根据傅立叶谱给出声音信号的各主要频率组成。 3.利用软件,设置恰当的数据采集间隔及采集时间,给出RLC瞬态电路及耦合电路信号图 及对应傅立叶谱图,根据两傅立叶谱找出两信号的中心频率,根据RLC电路理论解释瞬态 电路及耦合电路对应傅立叶谱图的中心频率分布特点
信号傅立叶分析项目 一. 基本原理 在科学技术的各个领域,存在各种复杂的信号。不管信号多复杂都可以分解为不同频率 的正弦分量。频谱函数描述了信号含有的正弦分量的频率和振幅的关系,是信号最基本的特 征之一。信号的傅立叶分析就是计算信号的频谱函数。 周期函数的频谱函数 周期为 T 的周期信号 可以展开成傅立叶级数: ¥ 0 n 0n 0 n=1 f(t)= a + a cos(2 n t)+ b sin(2 n t)] ∑ πν πν 0 1 (0) [cos(2 ) ( )] n n C C nt n πν φ ∞ = =+ + ∑ 式中: 2 2 () , Cn a b = +n n 1 () ( ) n tg d λ ϕ − = 分别是 n 次谐波的振幅和相位。把才 C(n)看作是 n 或 2πnν0的函数,称为振幅频谱。 φ(n)看作是是 n 或 2πnν0的函数,称为相位频谱。一般情况下只要知道振幅频谱就够 了,因而通常所称的频谱是指振幅频谱。 非周期函数的频谱函数 非周期函数可以看作是周期函数当周期趋向于∞ 时的极限情况。只要将周期函数的傅 立叶级数改写成傅立叶积分即可得相似的结果。 二.实验内容及要求 1.利用软件,给出信号发生器的周期信号(方波,正弦波,之字形波)图及对应傅立叶谱 图,根据傅立叶谱找出信号的中心频率。 2.利用软件,根据傅立叶谱给出声音信号的各主要频率组成。 3.利用软件,设置恰当的数据采集间隔及采集时间,给出 RLC 瞬态电路及耦合电路信号图 及对应傅立叶谱图,根据两傅立叶谱找出两信号的中心频率,根据 RLC 电路理论解释瞬态 电路及耦合电路对应傅立叶谱图的中心频率分布特点

三,实验室仪器、设备 实验室仪器 模拟信号装置
三.实验室仪器、设备 实验室仪器 模拟信号装置

麦克风及声音信号的傅立叶谱 YYYYWWWWWWW 平再 9Z9 臣宝 由 由 田 出 出 出 密
麦克风及声音信号的傅立叶谱
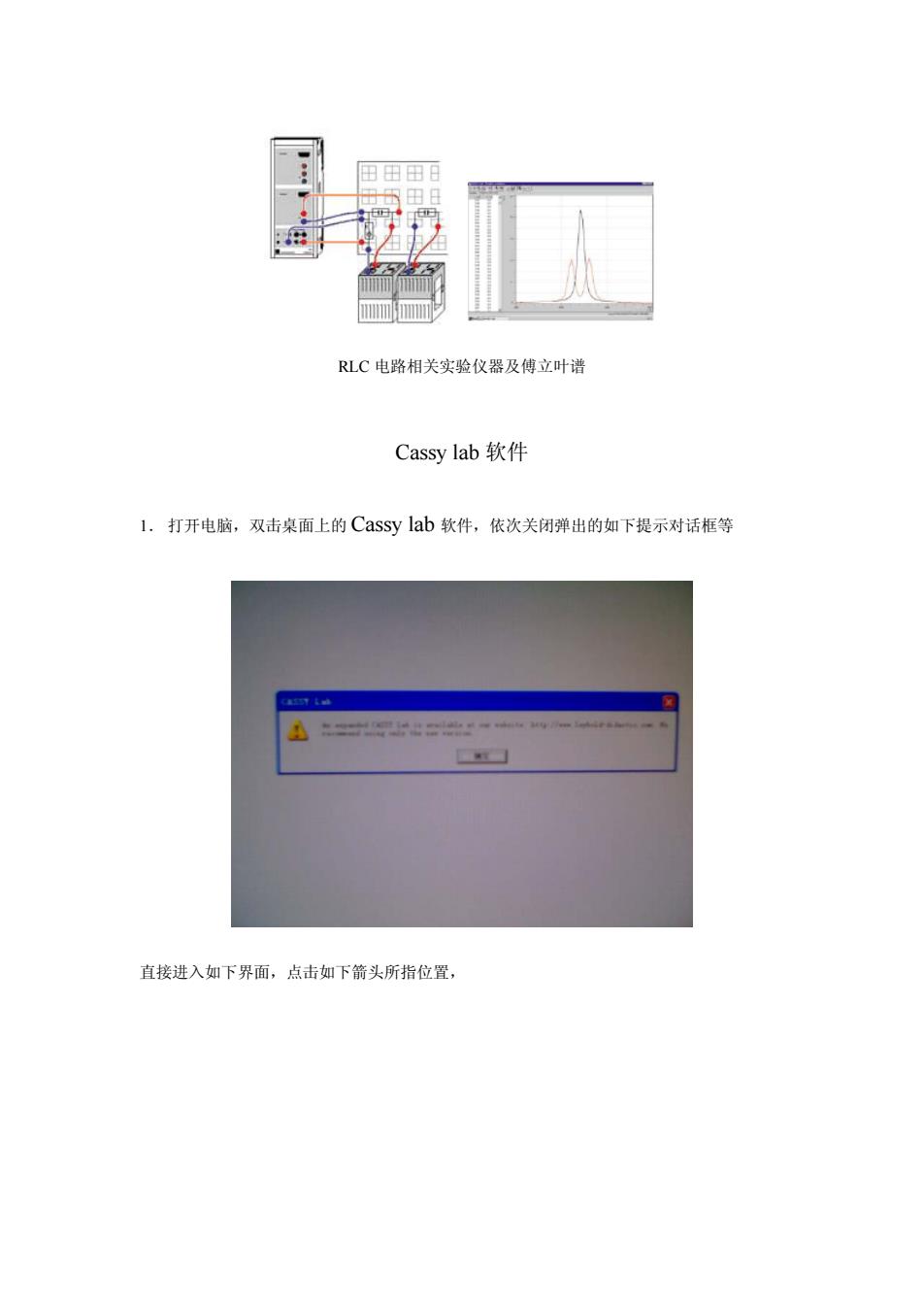
田田田目 面田日 LC电路相关实验仪器及傅立叶谱 Cassy lab软件 l.打开电脑,双击桌面上的Cassy lab软件,依次关闭弹出的如下提示对话框等 直接进入如下界面,点击如下箭头所指位置
RLC 电路相关实验仪器及傅立叶谱 Cassy lab 软件 1. 打开电脑,双击桌面上的 Cassy lab 软件,依次关闭弹出的如下提示对话框等 直接进入如下界面,点击如下箭头所指位置

在如下界面,进行电压设置,在点击箭头所指设置项, ( m
在如下界面,进行电压设置,在点击箭头所指设置项

如果没有得到如下界面,则点击New Quantity,选中快速傅立叶变换按钮。在最下方的参数 设置栏,可适当选择测量间隔及测量点数。在进行瞬态电路信号和耦合电路信号的测量时, 须选择触发,触发值小于0.01即可。此时,软件设置完毕,按下时钟按钮,可进行信号采 集。 注意:每次使用软件, 都需要对软件进行设置
如果没有得到如下界面,则点击 New Quantity,选中快速傅立叶变换按钮。在最下方的参数 设置栏,可适当选择测量间隔及 测量点数。在进行瞬态电路信号和耦合电路信号的测量时, 须选择触发,触发值小于 0.01 即可。此时,软件设置完毕,按下时钟按钮,可进行信号采 集。 注意:每次使用软件,都需要对软件进行设置