
PASCO物理组合实验系列 转动系统组合实验 周红编译 上海交通大学物理实验中心
PASCO 物理组合实验系列 转动系统组合实验 周红 编译 上海交通大学物理实验中心

目录 引言 I 实验】质点的转动惯量… 1 实验2向心力 4 实验3质点的角动量守恒… 8 实验4圆盘和圆环的转动惯量… 12 实验5圆盘绕偏轴的转动惯量(固定轴/转动轴) 16 实验6角动量守恒…19 演示实验六例… 21 实验一角动量守恒… 23 实验二向心力… 27 实验三证明角动量守恒: 30 实验四旋转马达… 31 实验五 旋转加逆水槽 32 实验六法拉第定律… 34
目 录 引言·································································································································· Ⅰ 实验1 质点的转动惯量································································································ 1 实验 2 向心力··············································································································· 4 实验3 质点的角动量守恒······························································································ 8 实验4 圆盘和圆环的转动惯量···················································································· 12 实验 5 圆盘绕偏轴的转动惯量(固定轴/转动轴)·················································· 16 实验6 角动量守恒········································································································ 19 演示实验六例·················································································································· 21 实验一 角动量守恒······································································································ 23 实验二 向心力·············································································································· 27 实验三 证明角动量守恒······························································································ 30 实验四 旋转马达·········································································································· 31 实验五 旋转加逆水槽·································································································· 32 实验六 法拉第定律······································································································ 34

转动系统组合实验 引言 Pascos的该套装置提供了一系列的向心力和转动动力学的实验,它包括了一坚实的底 座,一旋转平台,一T型沟槽,一套向心力装置和一套转动惯量装置,同时该系统提供一 750接口,通过一轻质滑轮来测量该装置的运动情况
转动系统组合实验 引言 Pascos 的该套装置提供了一系列的向心力和转动动力学的实验,它包括了一坚实的底 座,一旋转平台,一 T 型沟槽,一套向心力装置和一套转动惯量装置,同时该系统提供一 750 接口,通过一轻质滑轮来测量该装置的运动情况。 1

实验1质点的转动惯量 实验装置 A型底座 旋转平台 轻质滑轮及计时程序 砝码等 实验目的 测量质点的转动惯量,并证明它与理论值相一致。 实验原理 由理论可知,一个质点的转动惯量可由公式I=MR给出,其中M是质量,R是质点至转轴 的距离。 实验时可将一已知力矩作用于物体上,且其产生的角加速度可测出。因为t=α, I=va 其中a是角加速度,等于r,t是由悬挂的砝码产生的力矩。绳子缠绕在装置底坐上,其上 有卡口,用于卡绳头。R是绕绳圆半径,T是装置转动时绳中张力。 运用牛顿第二定律,得ΣF=mg-T=ma(见图1.1) rotating platform "A"base mg hanging mass 图1.1转动惯量装置和隔离体图 绳中张力为: T=m (g-a) 因为砝码的线加速度可测得,则通过计算就可测得T及。 实验内容 1.调节底座水平 实验前,必须仔细地调节底座的水平,如果导轨不水平,实验就会有影响,在加上附件 以前,先按下列步骤调水平。 (1)在导轨外侧加上一300g砝码,先使装置不平衡,拧紧螺丝使之固定。 (2)调整A型底座上的底脚螺丝直至导轨有砝码的一侧与另一底脚螺丝成一线,见图 1.2
实验 1 质点的转动惯量 实验装置 A 型底座 轻质滑轮及计时程序 旋转平台 砝码等 实验目的 测量质点的转动惯量,并证明它与理论值相一致。 实验原理 由理论可知,一个质点的转动惯量可由公式I=MR2 给出,其中M是质量,R是质点至转轴 的距离。 实验时可将一已知力矩作用于物体上,且其产生的角加速度可测出。因为 τ=Iα, I=τ/α 其中 α 是角加速度,等于 a/r,τ 是由悬挂的砝码产生的力矩。绳子缠绕在装置底坐上,其上 有卡口,用于卡绳头。R 是绕绳圆半径,T 是装置转动时绳中张力。 运用牛顿第二定律,得ΣF=mg-T=ma(见图 1.1) 图 1.1 转动惯量装置和隔离体图 绳中张力为: T=m(g-a) 因为砝码的线加速度可测得,则通过计算就可测得 T 及 α。 实验内容 1. 调节底座水平 实验前,必须仔细地调节底座的水平,如果导轨不水平,实验就会有影响,在加上附件 以前,先按下列步骤调水平。 (1) 在导轨外侧加上—300g 砝码,先使装置不平衡,拧紧螺丝使之固定。 (2) 调整 A 型底座上的底脚螺丝直至导轨有砝码的一侧与另一底脚螺丝成一线,见图 1.2。 1
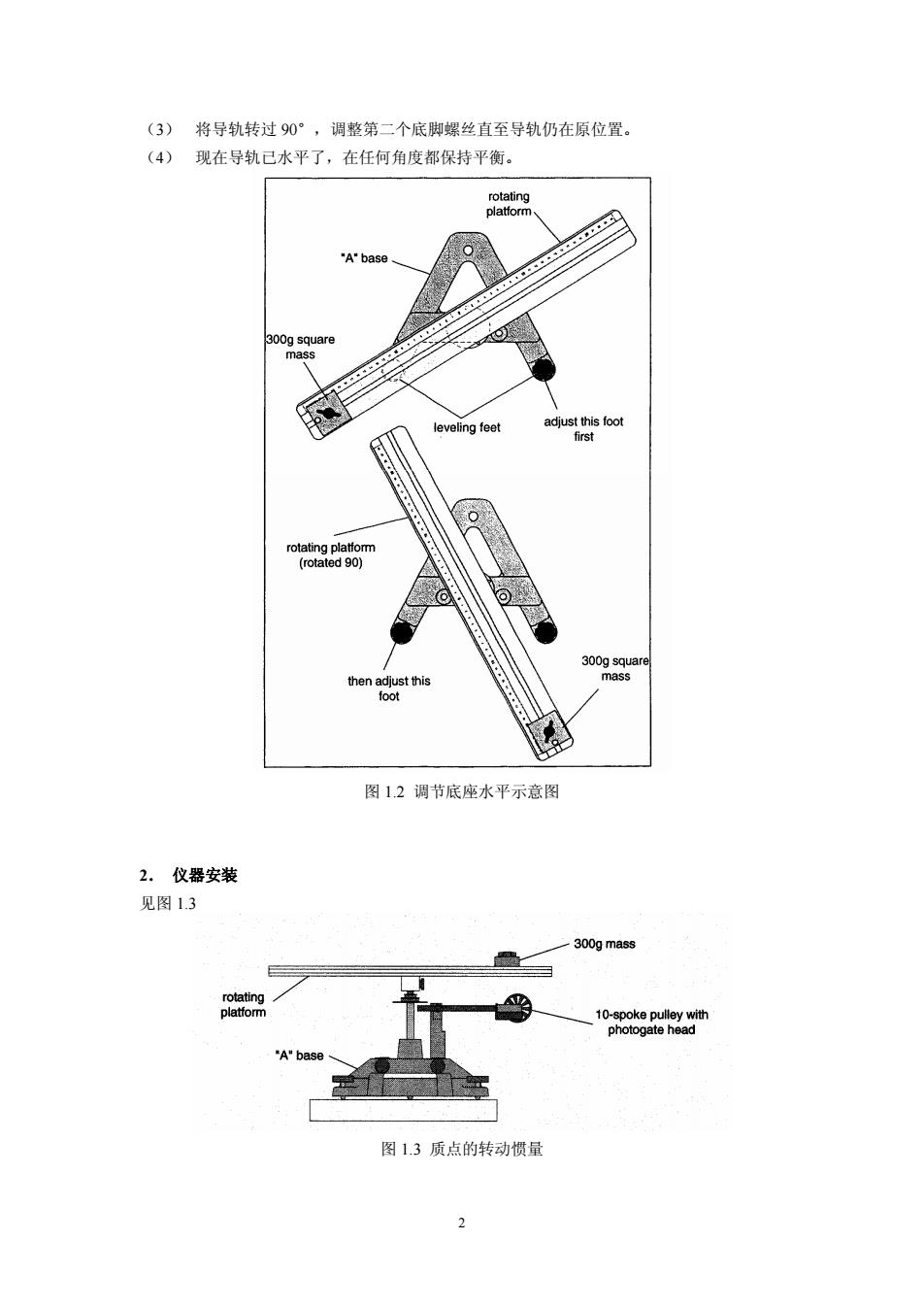
(3) 将导轨转过90°,调整第二个底脚螺丝直至导轨仍在原位置。 (4)现在导轨已水平了,在任何角度都保持平衡。 rotating platform "A"base 300g square mass leveling feet adjust this foot first rotating platform (rotated 90) 300g square then adjust this mass foot 图1.2调节底座水平示意图 2.仪器安装 见图1.3 300g mass rotating platform 10-spoke pulley wi地h photogate head "A"base 图1.3质点的转动惯量 2
(3) 将导轨转过 90°,调整第二个底脚螺丝直至导轨仍在原位置。 (4) 现在导轨已水平了,在任何角度都保持平衡。 图 1.2 调节底座水平示意图 2. 仪器安装 见图 1.3 图 1.3 质点的转动惯量 2

3.实验内容 第一部分:理论值测量 测量质量(M)及质点至转轴中心的距离。 表1.1转动惯量理论值 质量(g) 半径(cm) 第二部分测量实验值 1.寻找摩擦力 通常在做测量转动惯量的理论分析时,并没有考虑摩擦力。在实验中要设法补偿。即找 用于克服摩擦力的砝码的大小,即使砝码在下落过程中作匀速成运动。那么这“摩擦质量” 将被从总质量中减去。 2.利用计算机测量速度程序,确定“摩擦质量”,即在滑轮下挂足够重的砝码,使得它做 匀速运动,且测量速度时,要求三位有效位数字相同。 2
3. 实验内容 第一部分:理论值测量 测量质量(M)及质点至转轴中心的距离 r。 表 1.1 转动惯量理论值 质量(g) 半径(cm) 第二部分 测量实验值 1. 寻找摩擦力 通常在做测量转动惯量的理论分析时,并没有考虑摩擦力。在实验中要设法补偿。即找 用于克服摩擦力的砝码的大小,即使砝码在下落过程中作匀速成运动。那么这“摩擦质量” 将被从总质量中减去。 2. 利用计算机测量速度程序,确定“摩擦质量”,即在滑轮下挂足够重的砝码,使得它做 匀速运动,且测量速度时,要求三位有效位数字相同。 3

实验2向心力 实验装置 向心力装置 曲线纸(2张) 旋转平台 砝码和悬挂支架 秒表 线 天平 实验目的 研究在一圆形轨道上旋转的物体,不同的物体质量,圆的半径对该物体所受向心力的影 响。 实验原理 当一质量为的物体系在一长度为L的绳上并绕一水平圆旋转,则该物上的向心力为: F=m -mro2 其中v为切向速度,o为角速度(v=@)。通过测量旋转一周的时间(周期T)得到速度 T 则向心力为: FA4πmr T2 安装 参阅“A”底座及旋转平台法安装该装置。 实验内容 第一部分不同半径(力和质量恒定不变) (1)向心力和悬挂物的质量在这部分保持不变。称衡该物体并在表2.1中记录,在边柱 上悬挂起物体,并将之通过线与弹簧连接起来,线必须通过中央柱体上的滑轮。 (2)把带夹头的滑轮安装在导轨的靠近悬挂物的一端,按图2.1挂上砝码,在表2.1中记 录下该砝码的质量,这样就有了恒向心力。 (3)边柱刻线所对应位置长是所选择半径,安装边柱时要使之垂直并拧紧支架螺丝。在 表2.1中记录该半径。 (4)边柱上的悬挂物必须垂直悬挂,调节中央柱顶端的弹簧支架直至边柱刻线与物体悬 线重合。 (5)调节指示支架,使之与橙色指示器重合。 (6)移开滑轮上的重物以及滑轮
实验 2 向心力 实验装置 向心力装置 旋转平台 秒表 天平 曲线纸(2 张) 砝码和悬挂支架 线 实验目的 研究在一圆形轨道上旋转的物体,不同的物体质量,圆的半径对该物体所受向心力的影 响。 实验原理 当一质量为 m 的物体系在一长度为 L 的绳上并绕一水平圆旋转,则该物上的向心力为: 2 2 mrω r mv F == 其中 v 为切向速度,ω 为角速度(v=rω)。通过测量旋转一周的时间(周期 T)得到速度 V= T 2πr 则向心力为: F= 2 2 4 T π mr 安装 参阅“A”底座及旋转平台法安装该装置。 实验内容 第一部分 不同半径(力和质量恒定不变) (1) 向心力和悬挂物的质量在这部分保持不变。称衡该物体并在表 2.1 中记录,在边柱 上悬挂起物体,并将之通过线与弹簧连接起来,线必须通过中央柱体上的滑轮。 (2) 把带夹头的滑轮安装在导轨的靠近悬挂物的一端,按图 2.1 挂上砝码,在表 2.1 中记 录下该砝码的质量,这样就有了恒向心力。 (3) 边柱刻线所对应位置长是所选择半径,安装边柱时要使之垂直并拧紧支架螺丝。在 表 2.1 中记录该半径。 (4) 边柱上的悬挂物必须垂直悬挂,调节中央柱顶端的弹簧支架直至边柱刻线与物体悬 线重合。 (5) 调节指示支架,使之与橙色指示器重合。 (6) 移开滑轮上的重物以及滑轮。 4

(7)转动装置,使之加速至橙色指示器与指示支架重合,这说明悬挂物再一次垂直。 string side post center post assembly assembly clamp-on pulley rotating platfomm hanging mass "A"base 图2.1向心力装置 (8) 保持该速度,用秒表记录转动周的时间,算出周期后记录在表2.1中。 (9) 移边柱至一新的半径处,重复上述过程,共做5个半径。 表2.1不同的半径 物体的质量= 挂在滑轮上的砝码质量= 直线的斜率= 半径 周期 2 说明 (1)通过滑轮悬挂的砝码就等于施于弹簧的向心力。该质量乘以“g”就是向心力,并记 录在表2.2中。 (2)计算出T2,记录在表2.1中。 (3)作图-T,它是线性的,因为r=(,F一)T: An2m (4)画出拟合直线,求出斜率,记录在表2.1中。 (5)利用斜率计算向心力,并记录在表2.2中。 (6)计算在表2.2中向心力的百分误差。 表2.2结果(不同半径) 向心力=mg 由斜率求出的向心力 百分误差
(7) 转动装置,使之加速至橙色指示器与指示支架重合,这说明悬挂物再一次垂直。 图 2.1 向心力装置 (8) 保持该速度,用秒表记录转动周的时间,算出周期后记录在表 2.1 中。 (9) 移边柱至一新的半径处,重复上述过程,共做 5 个半径。 表 2.1 不同的半径 物体的质量= 挂在滑轮上的砝码质量= 直线的斜率= 半径 周期 T2 说明 (1) 通过滑轮悬挂的砝码就等于施于弹簧的向心力。该质量乘以“g”就是向心力,并记 录在表 2.2 中。 (2) 计算出T2 ,记录在表 2.1 中。 (3) 作图r-T2 ,它是线性的,因为 2 2 ) 4 ( T m F r π = (4) 画出拟合直线,求出斜率,记录在表 2.1 中。 (5) 利用斜率计算向心力,并记录在表 2.2 中。 (6) 计算在表 2.2 中向心力的百分误差。 表 2.2 结果(不同半径) 向心力=mg 由斜率求出的向心力 百分误差 5

第二部分:改变力(半径和质量恒定不变) 在该实验部分,旋转半径及悬挂物的质量保持恒定。 (1)称衡该物体并记录在表2.3中,在边柱上悬挂该物体并通过绳将之与弹簧连接起来, 绳子必须通过在中央柱上的滑轮。(2)-(8)同第一部分的(2)·(8)。 (9)改变向心力:悬挂上不同质量的砝码。保持半径不变从(4)开始重复,共改变5 次力的大不。 表2.3不同的向心力 物体质量= 半径= 直线的斜率= 挂在滑轮上的砝码质量 向心力=mg 周期(T) 1/T2 说明 (1) 通过滑轮悬挂的砝码的重量就等于作用在弹簧上的向心力,将悬挂砝码的质量乘以 “g”即得到每次实验的向心力记录在表2.3中。 (2) 计算出每次实验的T2的倒数,并记录在表2.3中。 (3) 画出F~ 下图,它是线性的,因为:F=4nm T2 (4) 画出拟合直线并求出斜率,记录在表2.3中。 (5) 从斜率中计算出质量并记录在表2.4中。 (6)计算出二者的百分误差,并记录在表24中。 表2.4结果(不同的向心力) 物体的质量 物体的质量(斜率求得) 百分误差 第三部分改变质量(半径和向心力保持恒定) 在实验的该部分中,向心力和旋转半径保持不变。 (1)称衡附加砝码的质量,并记录在表2.5中,其(2)·(8)同第一部分(2)·(8) (2)改变侧面砝码的质量,保持半径不变,测定新的周期,重新称衡物体的质量,并记 录在表2.5中。 6
第二部分:改变力(半径和质量恒定不变) 在该实验部分,旋转半径及悬挂物的质量保持恒定。 (1) 称衡该物体并记录在表 2.3 中,在边柱上悬挂该物体并通过绳将之与弹簧连接起来, 绳子必须通过在中央柱上的滑轮。(2)-(8)同第一部分的(2)-(8)。 (9) 改变向心力:悬挂上不同质量的砝码。保持半径不变从(4)开始重复,共改变 5 次力的大不。 表 2.3 不同的向心力 物体质量= 半径= 直线的斜率= 挂在滑轮上的砝码质量 向心力=mg 周期(T) 1/T2 说明 (1) 通过滑轮悬挂的砝码的重量就等于作用在弹簧上的向心力,将悬挂砝码的质量乘以 “g”即得到每次实验的向心力记录在表 2.3 中。 (2) 计算出每次实验的T2 的倒数,并记录在表 2.3 中。 (3) 画出 F~ 2 1 T 图,它是线性的,因为:F= 2 2 4 T π mr (4) 画出拟合直线并求出斜率,记录在表 2.3 中。 (5) 从斜率中计算出质量并记录在表 2.4 中。 (6) 计算出二者的百分误差,并记录在表 2.4 中。 表 2.4 结果(不同的向心力) 物体的质量 物体的质量(斜率求得) 百分误差 第三部分 改变质量(半径和向心力保持恒定) 在实验的该部分中,向心力和旋转半径保持不变。 (1) 称衡附加砝码的质量,并记录在表 2.5 中,其(2)-(8)同第一部分(2)-(8) (2) 改变侧面砝码的质量,保持半径不变,测定新的周期,重新称衡物体的质量,并记 录在表 2.5 中。 6

表2.5悬挂物的质量不同 挂在滑轮上的砝码质量= 向心力=mg= 半径= 物体质量 周期(T) 向心力计算值 百分误差 说明 (1) 通过滑轮所悬挂的质量就等于弹簧上的向心力,表2.5的表头上记录向心力mg。 (2) 利用公式F=4红m,计算每次实验的向心力,并记录在表25中。 T2 (3)计算每次实验的向心力和mg之间的%。 思考题 1.当半径增加时,旋转周期是增加还是减小? 2.当半径和旋转物体的质量保持恒定,周期增加时,向心力是增加还是减小? 3.当物体质量增加时,向心力是增加还是减小? >
表 2.5 悬挂物的质量不同 挂在滑轮上的砝码质量= 向心力=mg= 半径= 物体质量 周期(T) 向心力计算值 百分误差 说明 (1) 通过滑轮所悬挂的质量就等于弹簧上的向心力,表 2.5 的表头上记录向心力 mg。 (2) 利用公式 F= 2 2 4 T π mr ,计算每次实验的向心力,并记录在表 2.5 中。 (3) 计算每次实验的向心力和 mg 之间的%。 思考题 1. 当半径增加时,旋转周期是增加还是减小? 2. 当半径和旋转物体的质量保持恒定,周期增加时,向心力是增加还是减小? 3. 当物体质量增加时,向心力是增加还是减小? 7