
实验三用非线性电路研究混沌现象 长期以来,物理学用两类体系描述物质世界:以经典力学为核心的完全确定论描述一 幅完全确定的物质及其运动图象,过去、现在和未来都按照确定的方式稳定而有序地运行; 统计物理和量子力学的创立,提示了大量微观粒子运动的随机性,它们遵循统计规律,因 为大多数的复杂系统是随机和无序的,只能用概率论方法得到某些统计结果.确定论和随 机性是相互独立的两套体系,分别在各自领域里成功地描述过世界.混沌的英文意思是混 乱的,无序的.由于长久以来世界各地的物理学家都在探求自然的秩序,而面对无秩序的 现象如大气、骚动的海洋、野生动物数目的突然增减及心脏跳动和脑部的变化,却都显得 相当无知.这些大自然中不规则的部份,既不连续且无规律,在科学上一直是个谜.但是 在七十年代,美国和欧洲有少数的科学家开始穿越混乱来开辟一条出路。包括数学家、物 理学家、生物学家及化学家等等,所有的人都在找寻各种不规则间的共相.混沌的研究表 明,一个完全确定的系统,即使非常简单,由于自身的非线性作用、同样具有内在的随机 性.绝大多数非线性动力学系统,既有周期运动,又有混沌运动,而混沌既不是具有周期 性和对称性的有序,又不是绝对的无序,而是可用奇怪吸引子来描述的复杂的有序,混沌 是非周期的有序性.本实验将借助非线性电阻,从实验上对这一现象进行一番探索.混沌 (Chaos)研究是20世纪物理学的重大事件. 混沌研究最先起源于Lorenz研究天气预报时用到的三个动力学方程.后来的研究表明, 无论是复杂系统,如气象系统、太阳系,还是简单系统,如钟摆、滴水龙头等,皆因存在 着内在随机性而出现类似无轨,但实际是非周期有序运动,即混沌现象.现在混沌研究涉 及的领域包括数学、物理学、生物学、化学、天文学、经济学及工程技术的众多学科,并 对这些学科的发展产生了深远影响.混沌包含的物理内容非常广泛,研究这些内容更需要 比较深入的数学理论,如微分动力学理论、拓扑学、分形几何学等等.目前混沌的研究重 点已转向多维动力学系统中的混沌、量子及时空混沌、混沌的同步及控制等方面. 【实验目的】 1.学习有源非线性电阻的伏安特性; 2.通过研究一个简单的非线性电路,了解混沌现象和产生混沌的原因. 【实验原理】 实验所用电路原理图如图1所示.电路中电感L和电容C1、C2并联构成一个振荡电 路.方程如(1)所示: dUc_=G(Uc-Uc,)+i C2di dUc=GUe,-Ua)-gUc (1) Ldi=-Uc dt -16-
- 16 - 实验三 用非线性电路研究混沌现象 长期以来,物理学用两类体系描述物质世界:以经典力学为核心的完全确定论描述一 幅完全确定的物质及其运动图象,过去、现在和未来都按照确定的方式稳定而有序地运行; 统计物理和量子力学的创立,提示了大量微观粒子运动的随机性,它们遵循统计规律,因 为大多数的复杂系统是随机和无序的,只能用概率论方法得到某些统计结果.确定论和随 机性是相互独立的两套体系,分别在各自领域里成功地描述过世界.混沌的英文意思是混 乱的,无序的.由于长久以来世界各地的物理学家都在探求自然的秩序,而面对无秩序的 现象如大气、骚动的海洋、野生动物数目的突然增减及心脏跳动和脑部的变化,却都显得 相当无知.这些大自然中不规则的部份,既不连续且无规律,在科学上一直是个谜.但是 在七十年代,美国和欧洲有少数的科学家开始穿越混乱来开辟一条出路.包括数学家、物 理学家、生物学家及化学家等等,所有的人都在找寻各种不规则间的共相.混沌的研究表 明,一个完全确定的系统,即使非常简单,由于自身的非线性作用、同样具有内在的随机 性.绝大多数非线性动力学系统,既有周期运动,又有混沌运动,而混沌既不是具有周期 性和对称性的有序,又不是绝对的无序,而是可用奇怪吸引子来描述的复杂的有序,混沌 是非周期的有序性.本实验将借助非线性电阻,从实验上对这一现象进行一番探索.混沌 (Chaos)研究是 20 世纪物理学的重大事件. 混沌研究最先起源于Lorenz研究天气预报时用到的三个动力学方程.后来的研究表明, 无论是复杂系统,如气象系统、太阳系,还是简单系统,如钟摆、滴水龙头等,皆因存在 着内在随机性而出现类似无轨,但实际是非周期有序运动,即混沌现象.现在混沌研究涉 及的领域包括数学、物理学、生物学、化学、天文学、经济学及工程技术的众多学科,并 对这些学科的发展产生了深远影响.混沌包含的物理内容非常广泛,研究这些内容更需要 比较深入的数学理论,如微分动力学理论、拓扑学、分形几何学等等.目前混沌的研究重 点已转向多维动力学系统中的混沌、量子及时空混沌、混沌的同步及控制等方面. 【实验目的】 1.学习有源非线性电阻的伏安特性; 2.通过研究一个简单的非线性电路,了解混沌现象和产生混沌的原因. 【实验原理】 实验所用电路原理图如图 1 所示.电路中电感 L 和电容 C1、C2 并联构成一个振荡电 路.方程如(1)所示: 2 2 1 1 1 2 2 d d ( ) d d ( ) d d 1 1 2 C L C C C C C C L C U t i L G U U gU t U C G U U i t U C = − = − − = − + (1)
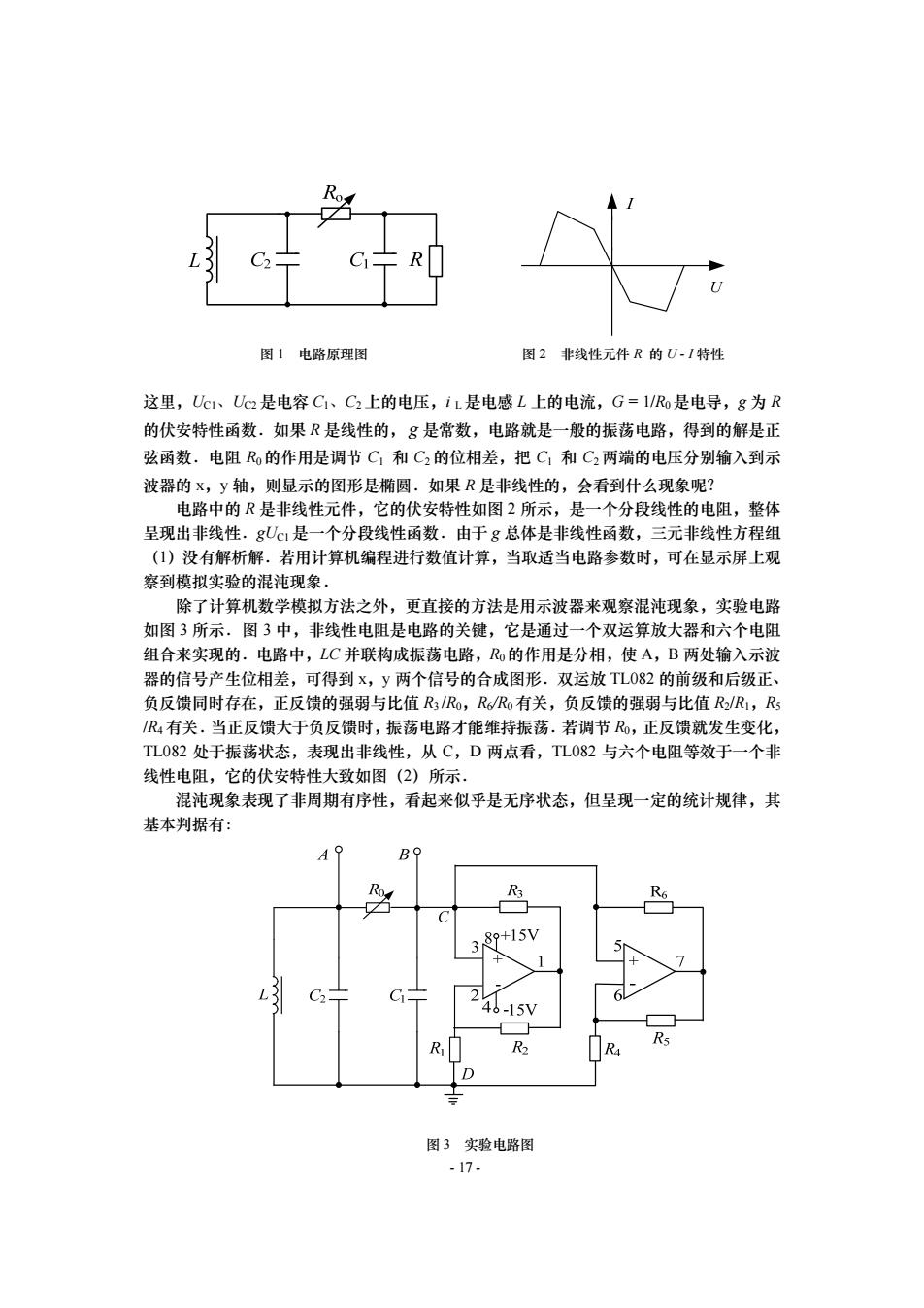
图1电路原理图 图2非线性元件R的U-I特性 这里,Uc1、UC2是电容C1、C2上的电压,iL是电感L上的电流,G=1/R是电导,g为R 的伏安特性函数.如果R是线性的,g是常数,电路就是一般的振荡电路,得到的解是正 弦函数.电阻R的作用是调节C:和C2的位相差,把C:和C2两端的电压分别输入到示 波器的X,y轴,则显示的图形是椭圆.如果R是非线性的,会看到什么现象呢? 电路中的R是非线性元件,它的伏安特性如图2所示,是一个分段线性的电阻,整体 呈现出非线性.gU1是一个分段线性函数.由于g总体是非线性函数,三元非线性方程组 (1)没有解析解.若用计算机编程进行数值计算,当取适当电路参数时,可在显示屏上观 察到模拟实验的混沌现象。 除了计算机数学模拟方法之外,更直接的方法是用示波器来观察混沌现象,实验电路 如图3所示.图3中,非线性电阻是电路的关键,它是通过一个双运算放大器和六个电阻 组合来实现的.电路中,LC并联构成振荡电路,R的作用是分相,使A,B两处输入示波 器的信号产生位相差,可得到x,y两个信号的合成图形.双运放TL082的前级和后级正、 负反馈同时存在,正反馈的强弱与比值R3/R,R6/Ro有关,负反馈的强弱与比值R2R1,R5 /R4有关.当正反馈大于负反馈时,振荡电路才能维持振荡.若调节R,正反馈就发生变化, TL082处于振荡状态,表现出非线性,从C,D两点看,TL082与六个电阻等效于一个非 线性电阻,它的伏安特性大致如图(2)所示. 混沌现象表现了非周期有序性,看起来似乎是无序状态,但呈现一定的统计规律,其 基本判据有: A Bo R3 3 89+15V L C2 C 2 46-15V R门 R2 图3实验电路图 -17-
- 17 - 这里,UC1、UC2 是电容 C1、C2 上的电压,i L是电感 L 上的电流,G = 1/R0是电导,g 为 R 的伏安特性函数.如果 R 是线性的, g 是常数,电路就是一般的振荡电路,得到的解是正 弦函数.电阻 R0 的作用是调节 C1 和 C2 的位相差,把 C1 和 C2 两端的电压分别输入到示 波器的 x,y 轴,则显示的图形是椭圆.如果 R 是非线性的,会看到什么现象呢? 电路中的 R 是非线性元件,它的伏安特性如图 2 所示,是一个分段线性的电阻,整体 呈现出非线性.gUC1 是一个分段线性函数.由于 g 总体是非线性函数,三元非线性方程组 (1)没有解析解.若用计算机编程进行数值计算,当取适当电路参数时,可在显示屏上观 察到模拟实验的混沌现象. 除了计算机数学模拟方法之外,更直接的方法是用示波器来观察混沌现象,实验电路 如图 3 所示.图 3 中,非线性电阻是电路的关键,它是通过一个双运算放大器和六个电阻 组合来实现的.电路中,LC 并联构成振荡电路,R0 的作用是分相,使 A,B 两处输入示波 器的信号产生位相差,可得到 x,y 两个信号的合成图形.双运放 TL082 的前级和后级正、 负反馈同时存在,正反馈的强弱与比值 R3 /R0,R6/R0 有关,负反馈的强弱与比值 R2/R1,R5 /R4 有关.当正反馈大于负反馈时,振荡电路才能维持振荡.若调节 R0,正反馈就发生变化, TL082 处于振荡状态,表现出非线性,从 C,D 两点看,TL082 与六个电阻等效于一个非 线性电阻,它的伏安特性大致如图(2)所示. 混沌现象表现了非周期有序性,看起来似乎是无序状态,但呈现一定的统计规律,其 基本判据有: 图 1 电路原理图 图 2 非线性元件 R 的 U - I 特性 图 3 实验电路图

1.频谱分析:R很小时,系统只有一个稳定的状态(对应一个解),随R的变化系统 由一个稳定状态变成在两个稳定状态之间跳跃(两个解),即由一周期变为二周期,进而两 个稳定状态分裂为四个稳定状态(四周期,四个解),八个稳定状态(八周期,八个解) 直至分裂进入无穷周期,即为连续频谱,接着进入混沌,系统的状态无法确定;分岔是进 入混沌的途径 2.无穷周期后,由于产生轨道排斥,系统出现局部不稳定; 3.奇异吸引子(Strange Attractor)存在.奇异吸引子有一个复杂但明确的边界,这个 边界保证了在整体上的稳定,在边界内部具有无穷嵌套的自相似结构,运动是混合和随机 的.它对初始条件十分敏感. 【实验仪器】 电源,实验接线板,数字万用表,非线性电阻,电容、电感和可调电位器,示波器。 元件参数如下: L=22mH,C1=10nF,C2=100nF,R1=3.3k2,R2=R3=22k2,R4=2.2k2, R=R6=220D,Ro是由的两个多圈电位器串联组成,可以进行粗调和细调. 【实验内容】 1.测量有源非线性电阻的伏安特性并画出伏安特性图 (1)因为非线性电阻是含源的,测量时不用电源,用电阻箱调节.伏特表并联在非线 性电阻两端,再和安培表、电阻箱串在一起构成回路 (2)尽量多测数据点.要求:测量间隔01V 测量范围13V 2.倍周期现象、周期性窗口、单吸引子和双吸引子的观察、记录和描述 将电容C1,C2上的电压输入到示波器的X,Y轴,先把R调到最小,示波器屏上可 观察到一条直线,调节,直线变成椭圆,到某一位置,图形缩成一点.增大示波器的倍 率,反向微调,可见曲线作倍周期变化,曲线由一周期增为二周期,由二周期倍增至四 周期,,直至一系列难以计数的无首尾的环状曲线,这是一个单涡旋吸引子集.再细 微调节,单吸引子突然变成了双吸引子,只见环状曲线在两个向外涡旋的吸引子之间不 断填充与跳跃,这就是混沌研究文献中所描述的“蝴蝶”图像,也是一种奇怪吸引子,它 的特点是整体上的稳定性和局域上的不稳定性同时存在· 利用这个电路,还可以观察到周期性窗口,仔细调节,有时原先的混沌吸引子不是 倍周期变化,却突然出现了一个三周期图像,再微调R,又出现混沌吸引子,这一现象称 为出现了周期性窗口.混沌现象的另一个特征是对于初值的敏感性 观察并记录不同倍周期时U一t图和Ro的值。 【思考题】 1.在正确连线的情况下,测量数据分布在(一、三)象限,而理论图为(二、四)象 限,为什么? 2.用计算机迭代求解方程x+1=1-xm2,k的取值范围为(0一2),迭代求解的方法是, 对一个k值,任意设定和,由上述方程可得到x1,由x可得到x2,如此求解下去.你会 -18-
- 18 - 1.频谱分析:R0 很小时,系统只有一个稳定的状态(对应一个解),随 R0 的变化系统 由一个稳定状态变成在两个稳定状态之间跳跃(两个解),即由一周期变为二周期,进而两 个稳定状态分裂为四个稳定状态(四周期,四个解),八个稳定状态(八周期,八个解)……… 直至分裂进入无穷周期,即为连续频谱,接着进入混沌,系统的状态无法确定;分岔是进 入混沌的途径. 2.无穷周期后,由于产生轨道排斥,系统出现局部不稳定; 3.奇异吸引子(Strange Attractor)存在.奇异吸引子有一个复杂但明确的边界,这个 边界保证了在整体上的稳定,在边界内部具有无穷嵌套的自相似结构,运动是混合和随机 的.它对初始条件十分敏感. 【实验仪器】 电源,实验接线板,数字万用表,非线性电阻,电容、电感和可调电位器,示波器. 元件参数如下: L = 22 mH,C1 = 10 nF, C2 = 100 nF, R1 = 3.3 kΩ, R2 = R3 = 22 kΩ,R4 = 2.2 kΩ, R5 = R6 = 220 Ω, R0 是由的两个多圈电位器串联组成,可以进行粗调和细调. 【实验内容】 1.测量有源非线性电阻的伏安特性并画出伏安特性图 (1)因为非线性电阻是含源的,测量时不用电源,用电阻箱调节.伏特表并联在非线 性电阻两端,再和安培表、电阻箱串在一起构成回路. (2)尽量多测数据点.要求:测量间隔 0.1 V 测量范围 13 V 2.倍周期现象、周期性窗口、单吸引子和双吸引子的观察、记录和描述 将电容 C1,C2 上的电压输入到示波器的 X,Y 轴,先把 R0 调到最小,示波器屏上可 观察到一条直线,调节 R0,直线变成椭圆,到某一位置,图形缩成一点.增大示波器的倍 率,反向微调 R0,可见曲线作倍周期变化,曲线由一周期增为二周期,由二周期倍增至四 周期,……,直至一系列难以计数的无首尾的环状曲线,这是一个单涡旋吸引子集.再细 微调节 R0,单吸引子突然变成了双吸引子,只见环状曲线在两个向外涡旋的吸引子之间不 断填充与跳跃,这就是混沌研究文献中所描述的“蝴蝶”图像,也是一种奇怪吸引子,它 的特点是整体上的稳定性和局域上的不稳定性同时存在. 利用这个电路,还可以观察到周期性窗口,仔细调节 R0,有时原先的混沌吸引子不是 倍周期变化,却突然出现了一个三周期图像,再微调 R0,又出现混沌吸引子,这一现象称 为出现了周期性窗口.混沌现象的另一个特征是对于初值的敏感性. 观察并记录不同倍周期时 Uc1-t 图和 R0 的值. 【思考题】 1.在正确连线的情况下,测量数据分布在(一、三)象限,而理论图为(二、四)象 限,为什么? 2.用计算机迭代求解方程 xn+1=1-kxn 2 ,k 的取值范围为(0-2),迭代求解的方法是, 对一个 k 值,任意设定 x0 ,由上述方程可得到 x1 ,由 x1 可得到 x2,如此求解下去.你会

发现对某些k值,可得到一个稳定的解,即一倍周期,某些k值,解在两个数值间跳跃, 即二倍周期,还会有四倍周期、八倍周期.直至无穷周期到混沌.尝试画出k一x图,并 分析.(x可取迭代500次以后的值) 3.分析讨论你所观察的混沌现象有哪些特征,并列举一些你所了解的混沌现象,以及 发生混沌现象的途径, 【参考文献】 [山华金龙等编.大学物理学(下册).上海:同济大学出版社,1996 [2]郝柏林.分岔、混沌、奇怪吸引子、湍流及其它.物理学进展,1983 3]赵凯华.从单摆到混沌.现代物理知识,1994 [4)郝柏林.从抛物线谈起一混沌动力学引论。上海:上海科技教有出版社,1993 [)张连芳等。非线性电路中混沌现象的模拟实验。工科物理增刊.北京:清华大学出版社,1998 [6E.H洛伦滋.混沌的本质.北京:气象出版社,1997 [7]P.R.Hobson and A.N.Lansbury.A simple electronic circuit to demonstrate bifurcation and chaos. Physics Education,1997 -19-
- 19 - 发现对某些 k 值,可得到一个稳定的解,即一倍周期,某些 k 值,解在两个数值间跳跃, 即二倍周期,还会有四倍周期、八倍周期……直至无穷周期到混沌.尝试画出 k—x 图,并 分析.(x 可取迭代 500 次以后的值) 3.分析讨论你所观察的混沌现象有哪些特征,并列举一些你所了解的混沌现象,以及 发生混沌现象的途径. 【参考文献】 [1] 华金龙等编.大学物理学(下册).上海:同济大学出版社,1996 [2] 郝柏林.分岔、混沌、奇怪吸引子、湍流及其它.物理学进展,1983 [3] 赵凯华.从单摆到混沌.现代物理知识,1994 [4] 郝柏林.从抛物线谈起——混沌动力学引论.上海:上海科技教育出版社,1993 [5] 张连芳等.非线性电路中混沌现象的模拟实验.工科物理增刊.北京:清华大学出版社,1998 [6] E.H.洛伦兹.混沌的本质.北京:气象出版社,1997 [7] P.R.Hobson and A.N.Lansbury. A simple electronic circuit to demonstrate bifurcation and chaos. Physics Education,1997