
良导热体铜、铝热导率的测量 热导率的动态测量在国际上已很普遍,方法也有多种。本实验采用热波法。其特点是当 热量在样品中转播时,样品各点的温度不像稳态法那样保持恒定。只要给定适当的边界条件, 就可以使得样品上的各点温度均可随时间作简谐变化,利用这种变化可计算出样品的热导 率。 【实验目的】 1.了解动态法的特点和其优越性 2.认识热波,加强对波动理论的理解 3.掌握一种测量热导率的方法 【实验原理】 令热量沿一维传播,故将样品制成棒状,周边隔热,取一小段样品讨论如图1所示。 Q+dQ X+dX 根据热转导定律,单位时间内流过任一垂直于转播方向面积A的热量,即热流为 Q=-kA4T (1) 其中K为待测材料的热导率, 是温度对坐标X的剃度。 dx 将(1)式两边对坐标取微分有 d0=-K447 dx2 根据能量守恒定律,任一时刻棒元的热平衡方程为 dT d'T CpAdx =d0=-k4 (2) dt 其中C,P分别为材料的比热容和密度,于是可得热流方程为 d=DT d (3) dr2 其中D= K ,称为热扩张系数。 Cp (3)式的解可把各点的温度随时间的变化表示出来,具体形式取决于边界条件。 若令热端的温度按简谐变化,即 T=To+T sin @t (4)
良导热体铜、铝热导率的测量 热导率的动态测量在国际上已很普遍,方法也有多种。本实验采用热波法。其特点是当 热量在样品中转播时,样品各点的温度不像稳态法那样保持恒定。只要给定适当的边界条件, 就可以使得样品上的各点温度均可随时间作简谐变化,利用这种变化可计算出样品的热导 率。 【实验目的】 1. 了解动态法的特点和其优越性 2. 认识热波,加强对波动理论的理解 3. 掌握一种测量热导率的方法 【实验原理】 令热量沿一维传播,故将样品制成棒状,周边隔热,取一小段样品讨论如图 1 所示。 T Q Q+dQ X X X+dX 图 1 根据热转导定律,单位时间内流过任一垂直于转播方向面积 A 的热量,即热流为 (1) dT Q KA dx = − 其中 K 为待测材料的热导率, dT dx 是温度对坐标 X 的剃度。 将(1)式两边对坐标取微分有 2 2 d T dQ KA dx dx = − 根据能量守恒定律,任一时刻棒元的热平衡方程为 2 2 (2) dT d T C Adx dQ KA dx dt dx = = − 其中 C,ρ分别为材料的比热容和密度,于是可得热流方程为 2 2 (3) dT d T D dt dx = 其中 K D C = ,称为热扩张系数。 (3)式的解可把各点的温度随时间的变化表示出来,具体形式取决于边界条件。 若令热端的温度按简谐变化,即 0 sin (4) T T T t = + m

另一端用冷水冷却,保持恒定的低温T,则(3)式的解也就是棒中各点的温度。为 四 T=To-ax+Te V2D'xsin(@t- 0 x) (5) V2D 其中T,是直流成分,α是线性成分的斜率。从上式得出: (1)热端(x=O)处温度按简谐方式变化时,这种变化将以衰减的形式在棒内向冷端传播, 称为热波,或温度波。 (2)热波的波速:V=√2Do (6) (3)热波的波长:V=2π 2D (7) 因此在热端温度变化的角频率ω以知的情况下,只要测出波速或波长就可计算出D,而后再 有D= 计算出材料的热导率K。本实验采用(6)式可得 Cp 2=2 0 则 V'Cp_VCeT K= (8) Cp 4πf4π 其中,f、T分别为热端温度按简谐变化的频率和周期。 从上述原理可知实现热导率测量的关键是: (1) 如何实现热量的一维传播: (2)如何实现热断温度随时间按简谐形式变化的边界条件: 【实验仪器】 1.RB-1型热导率动态测量仪 工作方式:“手动”和“程控”两种: 热源功率:500W×2 脉动周期:手动方式:180土1(秒):程控方式:任意 样品温度有效范围:10℃~100℃ 温度分辨率:±0.5℃ 2.微型计算机(P5以上,RAM16M) 软件环境:Windows98 数据格式:标准文本格式 显示方式:动态实时显示测量曲线和数据 3.样品中的测量点分布及编号 从样品热端至冷端,沿轴样品轴线,每隔20mm分布1个热电偶传感器 “铜”样品有12个传感器,编号依次为1、2、3、4、5、6、7、8、9、10、11、12 “铝”样品有8个传感器,编号依次为1、2、3、4、5、6、7、8 4.有关参数
另一端用冷水冷却,保持恒定的低温 , T0 ,则(3)式的解也就是棒中各点的温度。为 2 0 sin( ) (5) 2 x D T T x T e x t x m D − = − + − 其中 T0 是直流成分,α是线性成分的斜率。从上式得出: (1)热端(x=0)处温度按简谐方式变化时,这种变化将以衰减的形式在棒内向冷端传播, 称为热波,或温度波。 (2)热波的波速: V D = 2 (6) (3)热波的波长: 2 2 (7) D V = 因此在热端温度变化的角频率ω以知的情况下,只要测出波速或波长就可计算出 D,而后再 有 K D C = 计算出材料的热导率 K。本实验采用(6)式可得 2 2 2 2 (8) 4 4 K V C V C V K T C f = = = 则 其中,f、T 分别为热端温度按简谐变化的频率和周期。 从上述原理可知实现热导率测量的关键是: (1) 如何实现热量的一维传播; (2) 如何实现热断温度随时间按简谐形式变化的边界条件; 【实验仪器】 1.RB-1 型热导率动态测量仪 工作方式:“手动”和“程控”两种; 热源功率:500W×2 脉动周期:手动方式:180±1(秒);程控方式:任意 样品温度有效范围:10℃~100℃ 温度分辨率:±0.5℃ 2.微型计算机(P5 以上,RAM>16M) 软件环境:Windows98 数据格式:标准文本格式 显示方式:动态实时显示测量曲线和数据 3.样品中的测量点分布及编号 从样品热端至冷端,沿轴样品轴线,每隔 20mm 分布 1 个热电偶传感器 “铜”样品有 12 个传感器,编号依次为 1、2、3、4、5、6、7、8、9、10、11、12 “铝”样品有 8 个传感器,编号依次为 1、2、3、4、5、6、7、8 4. 有关参数
铜的密度:8.9g/cm 铝的密度:2.7gcm3 铜的比热:0.38J/g·K 铜的比热:0.90J/g·K 【实验内容】 1.使用“程控”方式 2.测量“铜”样品(2~7)共6个点,“铝”样品(2~6)共5个点:(先铜后铝) 3.经过40~60分钟后系统稳定后,在曲线上利用光标键测量出各峰点的相关的数据,并将 曲线图复制下来: 【数据处理】 方法一: 将T~t曲线图打印出来,选定任意两条曲线,求出这两条正弦曲线与参考方波产生的相 位差△S=S-S,,以及测量点走过的距离△L和每个周期的长度S,可得出 1=(△S,/S)×T,T为方波的周期,并且设V为热波在样品中传播的速度,在走过了△L距 离后所需要的时间为t=△L,/W,所以传播的速度为V=△L,S/T△S,将V代入(8)式计 算热导率K=△L2S2Cρ/4πT△S2。也可用相应各组的K值取平均。如图2所示。 方法二: RB-1热导率动态测量仪 1440 1820 1710 1600 1890 190 20T0 2180 094 0g4 松 644
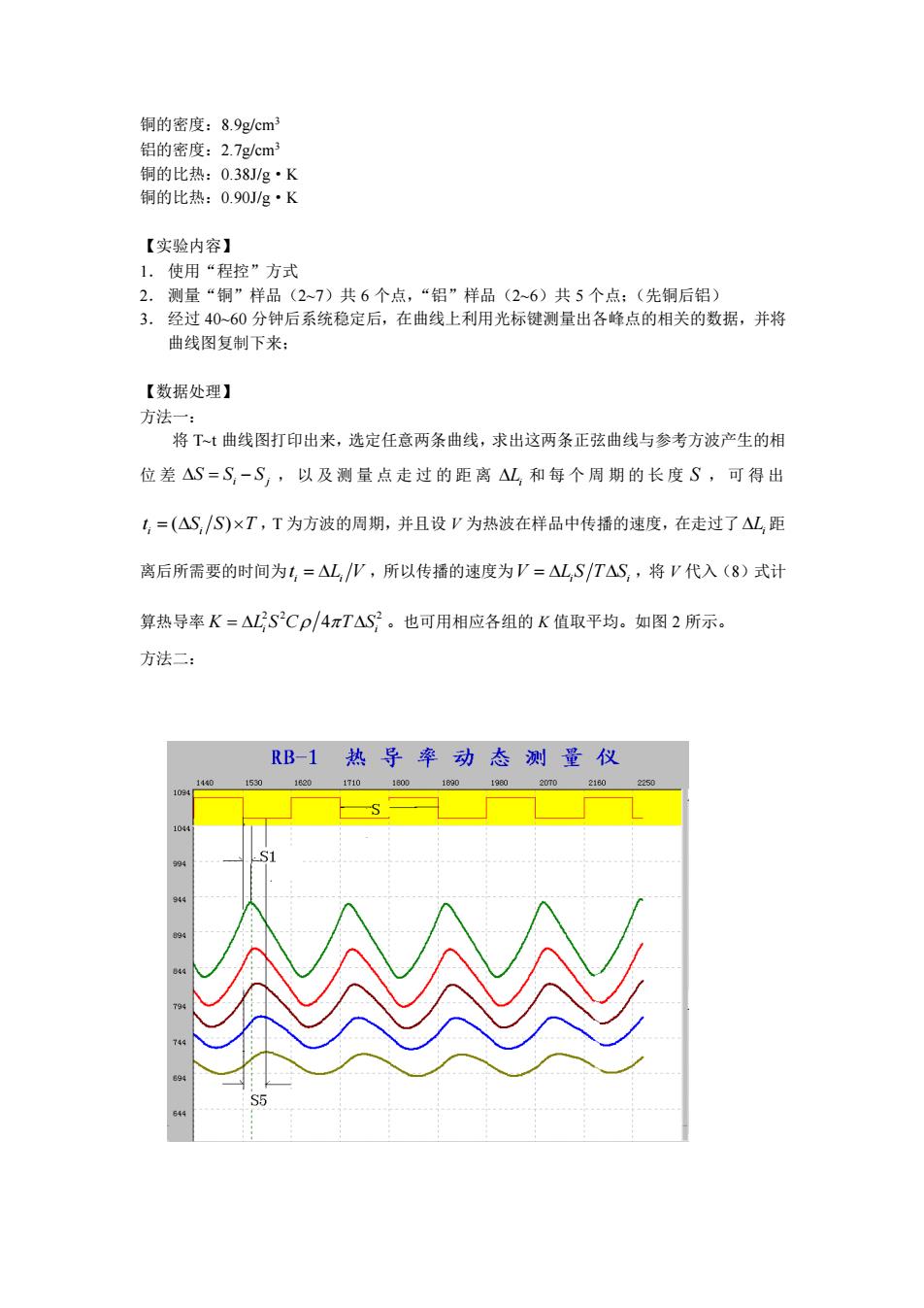
铜的密度:8.9g/cm3 铝的密度:2.7g/cm3 铜的比热:0.38J/g·K 铜的比热:0.90J/g·K 【实验内容】 1. 使用“程控”方式 2. 测量“铜”样品(2~7)共 6 个点,“铝”样品(2~6)共 5 个点;(先铜后铝) 3. 经过 40~60 分钟后系统稳定后,在曲线上利用光标键测量出各峰点的相关的数据,并将 曲线图复制下来; 【数据处理】 方法一: 将 T~t 曲线图打印出来,选定任意两条曲线,求出这两条正弦曲线与参考方波产生的相 位 差 i j = − S S S ,以及测量点走过的距离 Li 和每个周期的长度 S ,可得出 ( ) i i t S S T = ,T 为方波的周期,并且设 V 为热波在样品中传播的速度,在走过了 Li 距 离后所需要的时间为 i i t L V = ,所以传播的速度为 V L S T S = i i ,将 V 代入(8)式计 算热导率 2 2 2 4 K L S C T S = i i 。也可用相应各组的 K 值取平均。如图 2 所示。 方法二:

直接在显示屏上读取,求出任意各组的K值,通过(8)式可得:K=CpI仍一”厂 4π(t,-t) 【思考题】 1.如果想知道棒上某一时刻棒上的热波,即T~X曲线,将怎么做?画出它的大概形状。 2.用测出的数据计算热波波长: 3.为什么较后的测量点的T~t曲线会逐渐平坦而不呈现正弦波形?
直接在显示屏上读取,求出任意各组的 K 值,通过(8)式可得: 2 2 0 ( ) 4 ( ) i j i j C T n n l K t t − = − 【思考题】 1. 如果想知道棒上某一时刻棒上的热波,即 T~X 曲线,将怎么做?画出它的大概形状。 2. 用测出的数据计算热波波长; 3. 为什么较后的测量点的 T~t 曲线会逐渐平坦而不呈现正弦波形?