
光杠杆法测量金属的线胀系数 任何物体都具有“热胀冷缩”的特性,这个特性在工程设计、精密仪表设计、材料的焊接 和加工中都必须加以考虑。在一维情况下,固体受热后长度的增加称为线膨胀,我们用线膨胀 来表示固体的这种差别。 测定固体的线胀系数,实际上归结为测量在某一温度范围内的固体的微小伸长量。测量方 法有光杠杆法、螺旋测微法、干涉法等,本实验用光杠杆法,测量精确度极高。 【实验目的】 1.学会用光杠杆法测量固体长度的微小变化。 2.测量金属杆的线膨胀系数。 【实验原理】 固体加热时,体积将增大,这是一般物体所具有“热胀冷缩”的特性,固体受热后长度的 增长称为“线膨胀”,其长度L和温度之间的关系为 L=Lo(1+aT+BT+…) (1) 式中L为温度T=0℃时的长度。α、B…是和被测物质有关的常数,都是很小的数值。而B 以下各系数和ā相比甚小。所以在常温下可以忽略,则(1)式可写成: L=Lo(1+a T) (2) 式中ā就是通常所称的线胀系数,其物理意义为温度每升高一度时物体的伸长量与它在零度时 的长度比,单位是度分之一(℃) 如果在温度T和T2时,金属杆的长度分别为L和L2,则可写出: LI=Lo(1+a TD (3) L2=Lo (1+a T2) (4) 将式(3)代入式(4),化简后得: a = L21 (5) 4g-2) L 由于L2与L变化微小,L2/L≈1所以(5)式可近似写成 L2-L△L d (6) L(T3-T)L△1 测量线膨胀系数的主要问题是怎么测准温度变化引起长度的微小变化△L。 本实验采用光杠杆原理来测量长度的微小变化△L。 设D为镜面到标尺的距离,K为镜的单脚到双脚之距离。△X是温度由T。开始至T时望远 镜中标尺读数的增量。则: AL= K .△X (7) 2D 将式(7)代入式(6)得: K·△X a (8) 2DL (T,-T) 1
1 光杠杆法测量金属的线胀系数 任何物体都具有“热胀冷缩”的特性,这个特性在工程设计、精密仪表设计、材料的焊接 和加工中都必须加以考虑。在一维情况下,固体受热后长度的增加称为线膨胀,我们用线膨胀 来表示固体的这种差别。 测定固体的线胀系数,实际上归结为测量在某一温度范围内的固体的微小伸长量。测量方 法有光杠杆法、螺旋测微法、干涉法等,本实验用光杠杆法,测量精确度极高。 【实验目的】 1.学会用光杠杆法测量固体长度的微小变化。 2.测量金属杆的线膨胀系数。 【实验原理】 固体加热时,体积将增大,这是一般物体所具有“热胀冷缩”的特性,固体受热后长度的 增长称为“线膨胀”,其长度 L 和温度之间的关系为 L=L0(1+αT+βT 2 +……) (1) 式中 L0 为温度 T=0℃时的长度。α、β……是和被测物质有关的常数,都是很小的数值。而β 以下各系数和α相比甚小。所以在常温下可以忽略,则(1)式可写成: L=L0(1+αT) (2) 式中α就是通常所称的线胀系数,其物理意义为温度每升高一度时物体的伸长量与它在零度时 的长度比,单位是度分之一(℃—1) 如果在温度 T1 和 T2 时,金属杆的长度分别为 L1 和 L2,则可写出: L1=L0(1+αT1) (3) L2=L0(1+αT2) (4) 将式(3)代入式(4),化简后得: ( 1 ) 1 2 1 2 2 1 T L L L T L L − − = (5) 由于 L2 与 L1 变化微小,L2/ L1≈1 所以(5)式可近似写成 L T L L T T L L = − − = 1 2 1 1 2 1 ( ) (6) 测量线膨胀系数的主要问题是怎么测准温度变化引起长度的微小变化ΔL。 本实验采用光杠杆原理来测量长度的微小变化ΔL。 设 D 为镜面到标尺的距离,K 为镜的单脚到双脚之距离。ΔX 是温度由 T0 开始至 T1 时望远 镜中标尺读数的增量。则: X D K L = 2 (7) 将式(7)代入式(6)得: 2DL1(T2 T1 ) K X − = (8)

光杠杆原理示意图 本实验测定的金属杆为一般黄铜,它的线胀系数 as=1.89×105·℃-1 色 附图1501型超级恒温器 【实验仪器】: 1.501型超级恒温器 501型超级恒温器的外形如图1。它是金属圆筒形,筒盖板为黄铜制成,板上装有电动机 与水泵一套,接触温度计一支,液体进口嘴一只,发热器2组,冷凝管用进出水嘴2只,外筒 以钢板制成,内筒用黄铜板制,中垫以玻璃纤维作保温,电子继电器及供给电源部分,均装在 控制盒内。 温度能在0到100度之间调节,且能输出恒温的热水。 温度调节由接触温度计担任。将接触温度计选出恒温所需温度,开启加热开关,直到恒温 指示灯开始明灭状态表示温度已在恒温,此时可将加热开关关断,如标准温度计上所指的温度 不同于所需温度时,应再旋动接触温度计调整之。 接触温度计调温方法,旋转此温度计顶部之鼓形嵌以永久磁铁之胶木帽,利用磁场带动接 2
2 本实验测定的金属杆为一般黄铜,它的线胀系数 α标=1.89×10-5·℃—1 【实验仪器】: 1. 501 型超级恒温器 501 型超级恒温器的外形如图 1。它是金属圆筒形,筒盖板为黄铜制成,板上装有电动机 与水泵一套,接触温度计一支,液体进口嘴一只,发热器 2 组,冷凝管用进出水嘴 2 只,外筒 以钢板制成,内筒用黄铜板制,中垫以玻璃纤维作保温,电子继电器及供给电源部分,均装在 控制盒内。 温度能在 0 到 100 度之间调节,且能输出恒温的热水。 温度调节由接触温度计担任。将接触温度计选出恒温所需温度,开启加热开关,直到恒温 指示灯开始明灭状态表示温度已在恒温,此时可将加热开关关断,如标准温度计上所指的温度 不同于所需温度时,应再旋动接触温度计调整之。 接触温度计调温方法,旋转此温度计顶部之鼓形嵌以永久磁铁之胶木帽,利用磁场带动接 θ θ 2θ ΔL X 0 D K X 光杠杆原理示意图 附图 1 501 型超级恒温器
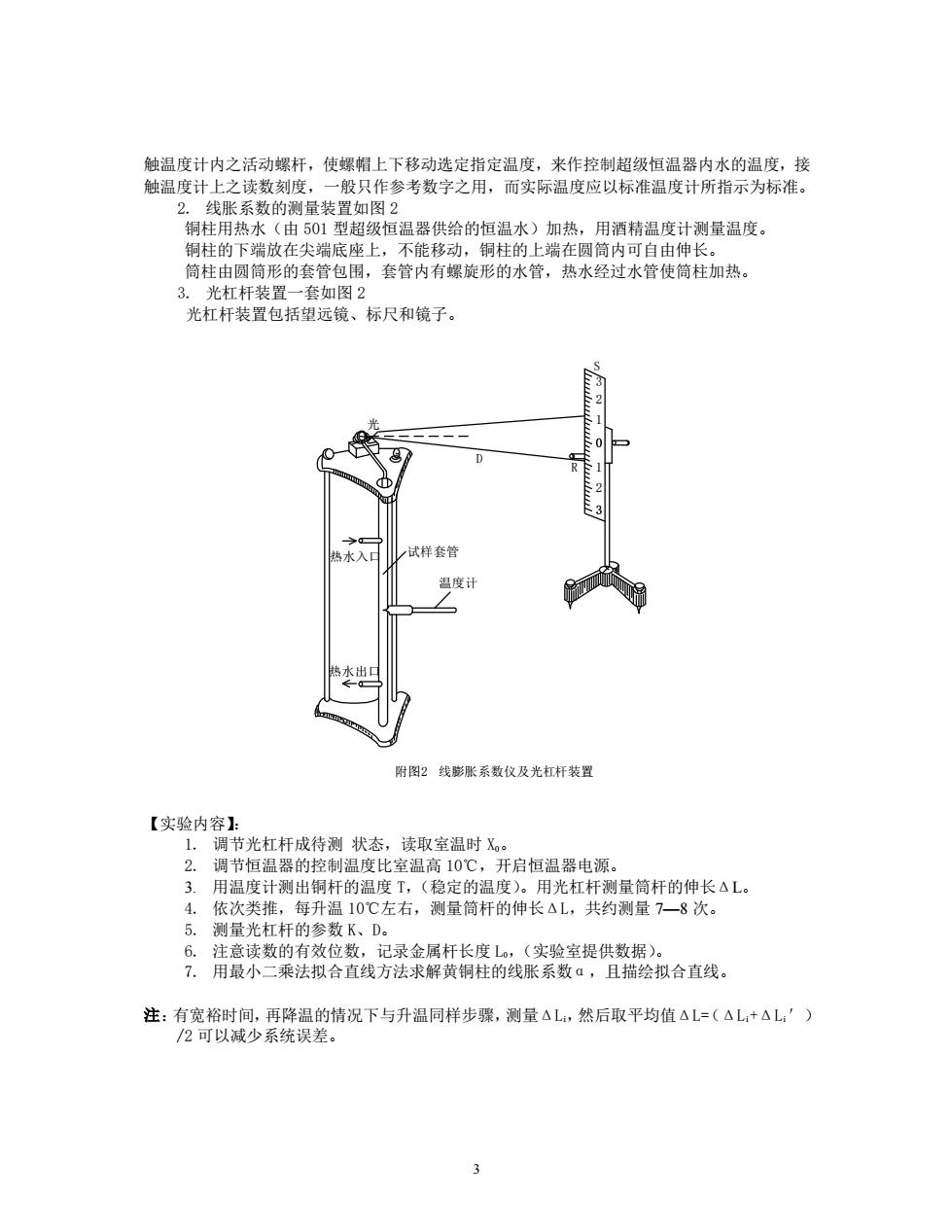
触温度计内之活动螺杆,使螺帽上下移动选定指定温度,来作控制超级恒温器内水的温度,接 触温度计上之读数刻度,一般只作参考数字之用,而实际温度应以标准温度计所指示为标准。 2.线胀系数的测量装置如图2 铜柱用热水(由501型超级恒温器供给的恒温水)加热,用酒精温度计测量温度。 铜柱的下端放在尖端底座上,不能移动,铜柱的上端在圆筒内可自由伸长。 筒柱由圆筒形的套管包围,套管内有螺旋形的水管,热水经过水管使筒柱加热。 3.光杠杆装置一套如图2 光杠杆装置包括望远镜、标尺和镜子。 热水入口 试样套管 温度计 热水出口 附图2线膨胀系数仪及光杠杆装置 【实验内容】: 1.调节光杠杆成待测状态,读取室温时X。 2.调节恒温器的控制温度比室温高10℃,开启恒温器电源。 3.用温度计测出铜杆的温度T,(稳定的温度)。用光杠杆测量筒杆的伸长△L。 4.依次类推,每升温10℃左右,测量筒杆的伸长△L,共约测量7一8次。 5.测量光杠杆的参数K、D。 6.注意读数的有效位数,记录金属杆长度L。,(实验室提供数据)。 7.用最小二乘法拟合直线方法求解黄铜柱的线胀系数α,且描绘拟合直线。 注:有宽裕时间,再降温的情况下与升温同样步骤,测量△L,然后取平均值△L=(△L+△L:') /2可以减少系统误差。 3
3 触温度计内之活动螺杆,使螺帽上下移动选定指定温度,来作控制超级恒温器内水的温度,接 触温度计上之读数刻度,一般只作参考数字之用,而实际温度应以标准温度计所指示为标准。 2. 线胀系数的测量装置如图 2 铜柱用热水(由 501 型超级恒温器供给的恒温水)加热,用酒精温度计测量温度。 铜柱的下端放在尖端底座上,不能移动,铜柱的上端在圆筒内可自由伸长。 筒柱由圆筒形的套管包围,套管内有螺旋形的水管,热水经过水管使筒柱加热。 3. 光杠杆装置一套如图 2 光杠杆装置包括望远镜、标尺和镜子。 【实验内容】: 1. 调节光杠杆成待测 状态,读取室温时 X0。 2. 调节恒温器的控制温度比室温高 10℃,开启恒温器电源。 3. 用温度计测出铜杆的温度 T,(稳定的温度)。用光杠杆测量筒杆的伸长ΔL。 4. 依次类推,每升温 10℃左右,测量筒杆的伸长ΔL,共约测量 7—8 次。 5. 测量光杠杆的参数 K、D。 6. 注意读数的有效位数,记录金属杆长度 L0,(实验室提供数据)。 7. 用最小二乘法拟合直线方法求解黄铜柱的线胀系数α,且描绘拟合直线。 注:有宽裕时间,再降温的情况下与升温同样步骤,测量ΔLi,然后取平均值ΔL=(ΔLi+ΔLi′) /2 可以减少系统误差。 3 2 1 0 1 2 3 D 试样套管 温度计 热水入口 热水出口 R 光 S 附图2 线膨胀系数仪及光杠杆装置

【预习题】 试分析哪一个量是影响本实验结果精度的主要因素? 【思考题】 1.两根材料相同、粗细长度不同的金属棒,在同样的温度变化范围内,它们的线膨胀系 数是否相同?膨胀量是否相同?为什么? 2.有一体积为V的各向同性物体,受热后其体积的相对增量跟温度的变化量成正比,即 △VN=B△T,其中B是比例系数,称为物体的体膨胀系数。试证明该物体的体膨胀系数B与 线膨胀系数α的关系。 4
4 【预习题】 试分析哪一个量是影响本实验结果精度的主要因素? 【思考题】 1. 两根材料相同、粗细长度不同的金属棒,在同样的温度变化范围内,它们的线膨胀系 数是否相同?膨胀量是否相同?为什么? 2. 有一体积为 V 的各向同性物体,受热后其体积的相对增量跟温度的变化量成正比,即 ΔV/V=βΔT,其中β是比例系数,称为物体的体膨胀系数。试证明该物体的体膨胀系数β与 线膨胀系数α的关系