
里德伯常数的测定 氢原子的光谱按波长(或波数)大小的排列次序上显示出简单的规律性,测量氢灯各光 谱线的波长值可以来了解原子的能级结构。本实验用分光计测量氢原子的光谱线波长,并通 过巴尔末公式推算里德伯常数。 原理 氢原子的光谱线在可见光区共有四条,分别用H。(红线)H。(蓝绿线)H,(青线) 和H。(紫线)记号来标志。他们的波数v(波长入的倒数)可以准确地用实验公式 v=R(221 (1) n 表示,式中n是大于2的整数,即3,4,5,…每一个数代表一条谱线,而R,是一个实验 常数,称为里德伯常数。式(1)就是著名的巴尔末公式。若利用分光计准确的测定上述四 条谱线的波长,并分别代入(1)式,即可由实验方法确定里德伯常数。此外,根据玻尔关 于原子构造的量子假设,里德伯常数与原子内部若干微观量和有关物理普适常数的关系是 e m Ru8c (2) MH 式中e为电子电荷,m为电子质量,Mn为氢原子核的质量,,”m= 1 M41836.5’c为光在真 空中的传播速度,6。为真空介电常数,h为普朗克常数。由此算出里德伯常数的理论值 Rg=1.09678×10'/m 光栅衍射 有大量等宽间隔的平行狭缝构成的光学元件成为光橱.设光栅的总缝数为N,缝宽为α, 缝间不透光部分为b,则缝距d=a+b,称为光栅常数.按夫琅和费光栅衍射理论,当一束 平行光垂直入射到光栅平面上时,通过不同的缝,光要发生干涉,但同时,每条缝又都要发 生衍射,且N条缝的N套衍射条纹通过透镜后将完全重合.如图1所示,当衍射角日满足 光栅方程dsin0=k2(k=0、±1、±2、…)时,任何两缝所发出的两束光都干涉相长,形 成细而亮的主极大明条纹. 1
1 里德伯常数的测定 氢原子的光谱按波长(或波数)大小的排列次序上显示出简单的规律性,测量氢灯各光 谱线的波长值可以来了解原子的能级结构。本实验用分光计测量氢原子的光谱线波长,并通 过巴尔末公式推算里德伯常数。 原理 氢原子的光谱线在可见光区共有四条,分别用 H (红线) H (蓝绿线) H (青线) 和 H (紫线)记号来标志。他们的波数 (波长 的倒数)可以准确地用实验公式 ) 1 2 1 ( 2 2 n = RH − (1) 表示,式中 n 是大于 2 的整数,即 3,4,5,…每一个数代表一条谱线,而 RH 是一个实验 常数,称为里德伯常数。式(1)就是著名的巴尔末公式。若利用分光计准确的测定上述四 条谱线的波长,并分别代入(1)式,即可由实验方法确定里德伯常数。此外,根据玻尔关 于原子构造的量子假设,里德伯常数与原子内部若干微观量和有关物理普适常数的关系是 (1 ) 8 2 3 0 4 H H M m m c h e R + = (2) 式中 e 为电子电荷,m 为电子质量, MH 为氢原子核的质量, 1836.5 1 = M H m ,c 为光在真 空中的传播速度, 0 为真空介电常数,h 为普朗克常数。由此算出里德伯常数的理论值 RH 1.09678 10 / m 7 = 光栅衍射 有大量等宽间隔的平行狭缝构成的光学元件成为光栅.设光栅的总缝数为 N,缝宽为 a, 缝间不透光部分为 b,则缝距 d = a + b,称为光栅常数.按夫琅和费光栅衍射理论,当一束 平行光垂直入射到光栅平面上时,通过不同的缝,光要发生干涉,但同时,每条缝又都要发 生衍射,且 N 条缝的 N 套衍射条纹通过透镜后将完全重合.如图 1 所示,当衍射角 满足 光栅方程 dsin = k(k = 0、1、 、 …)时,任何两缝所发出的两束光都干涉相长,形 成细而亮的主极大明条纹.
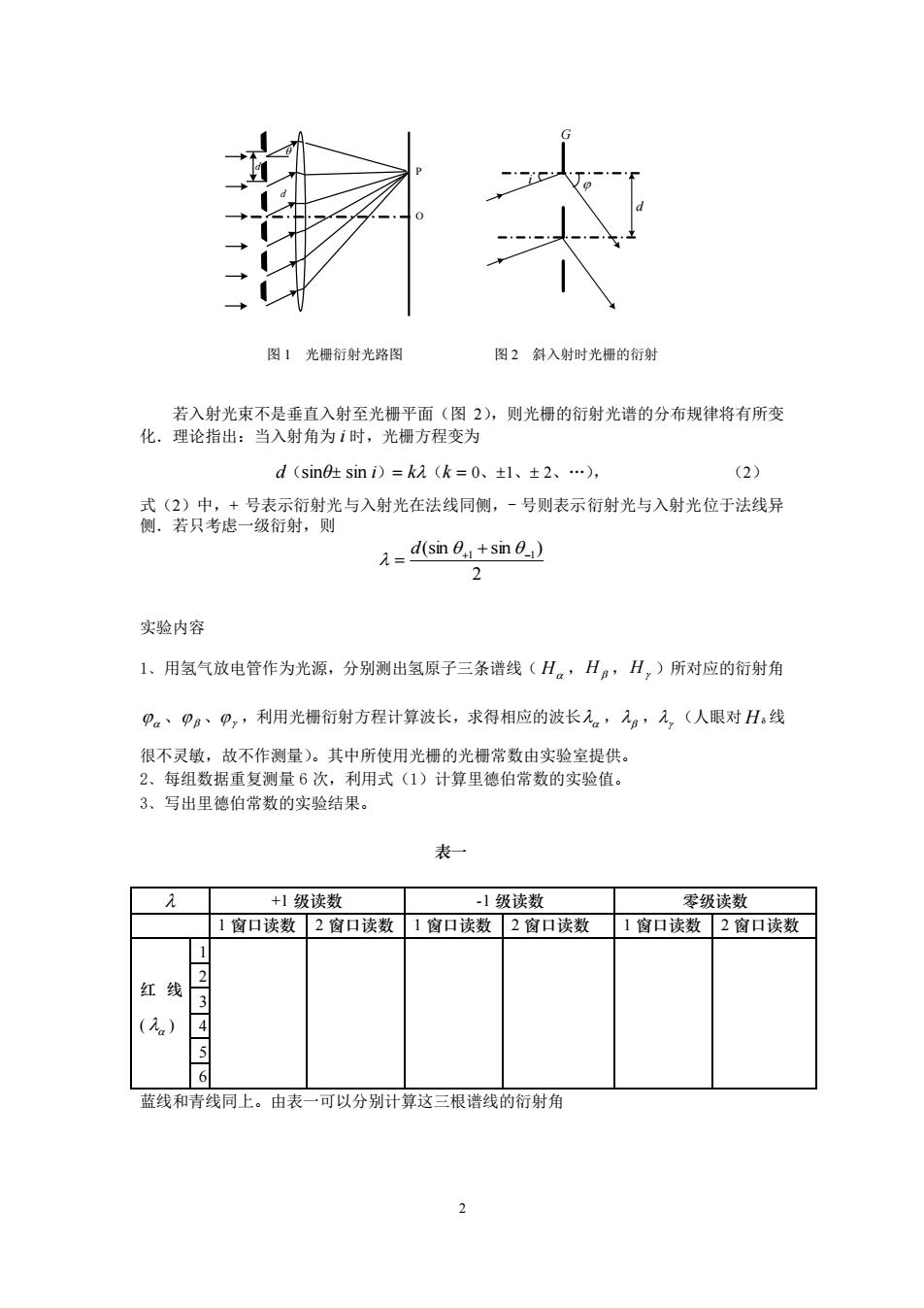
图1光栅衍射光路图 图2斜入射时光栅的衍射 若入射光束不是垂直入射至光栅平面(图2),则光栅的衍射光谱的分布规律将有所变 化.理论指出:当入射角为i时,光栅方程变为 d(sin0肚sini)=k2(k=0、±1、±2、…), (2) 式(2)中,+号表示衍射光与入射光在法线同侧,一号则表示衍射光与入射光位于法线异 侧.若只考虑一级衍射,则 d(sin +sin 2 实验内容 1、用氢气放电管作为光源,分别测出氢原子三条谱线(H。,H:,H,)所对应的衍射角 p。、pg、p,利用光栅衍射方程计算波长,求得相应的波长元a,g,入,(人眼对Hs线 很不灵敏,故不作测量)。其中所使用光栅的光栅常数由实验室提供。 2、每组数据重复测量6次,利用式(1)计算里德伯常数的实验值。 3、写出里德伯常数的实验结果。 表一 +1级读数 -1级读数 零级读数 1窗口读数2窗口读数1窗口读数2窗口读数 1窗口读数2窗口读数 1 红线 2 3 (a) 4 5 6 蓝线和青线同上。由表一可以分别计算这三根谱线的衍射角 2
2 d O d P G i d 图 1 光栅衍射光路图 图 2 斜入射时光栅的衍射 若入射光束不是垂直入射至光栅平面(图 2),则光栅的衍射光谱的分布规律将有所变 化.理论指出:当入射角为 i 时,光栅方程变为 d(sinθ sin i)= k(k = 0、1、 2、…), (2) 式(2)中,+ 号表示衍射光与入射光在法线同侧,- 号则表示衍射光与入射光位于法线异 侧.若只考虑一级衍射,则 2 (sin sin ) +1 + −1 = d 实验内容 1﹑用氢气放电管作为光源,分别测出氢原子三条谱线( H ,H ,H )所对应的衍射角 、 、 ,利用光栅衍射方程计算波长,求得相应的波长 , , (人眼对 H 线 很不灵敏,故不作测量)。其中所使用光栅的光栅常数由实验室提供。 2﹑每组数据重复测量 6 次,利用式(1)计算里德伯常数的实验值。 3﹑写出里德伯常数的实验结果。 表一 +1 级读数 -1 级读数 零级读数 1 窗口读数 2 窗口读数 1 窗口读数 2 窗口读数 1 窗口读数 2 窗口读数 红 线 ( ) 1 2 3 4 5 6 蓝线和青线同上。由表一可以分别计算这三根谱线的衍射角

波长及里德伯常数见表二。 表二 p±0。() ±o,(A) RH±o(m) a B R,的平均值及标准偏差为 RH±OR=( )x/m 思考题 1.氢原子在可见区、红外区、紫外区的所有谱线可统一用一个简单的公式表示: =RH( 11 式中n=l、2、3、…:=n+1、n+2…。根据什么原则来选定各氢光谱线的n的可能 值是正确值?nm又怎 线来判断所选定n的正确性及求得n。) 2.光谱中若出现不属于氢的谱线,应如何判断? 3
3 波长及里德伯常数见表二。 表二 (°) ( A ) ( ) −1 R m H RH RH 的平均值及标准偏差为 H ˆ ( /m ) R R = 思考题 1. 氢原子在可见区、红外区、紫外区的所有谱线可统一用一个简单的公式表示: 2 2 1 1 ( ) H oi R n n = − 式中 oi n =1﹑2﹑3﹑… ;n= oi n +1﹑ oi n +2…。根据什么原则来选定各氢光谱线的 n 的可能 值?又怎么来判别某个 n 值的可能值是正确值? oi n 又怎么求得呢?(提示:可作 2 1 n − 图 线来判断所选定 n 的正确性及求得 oi n 。) 2.光谱中若出现不属于氢的谱线,应如何判断?
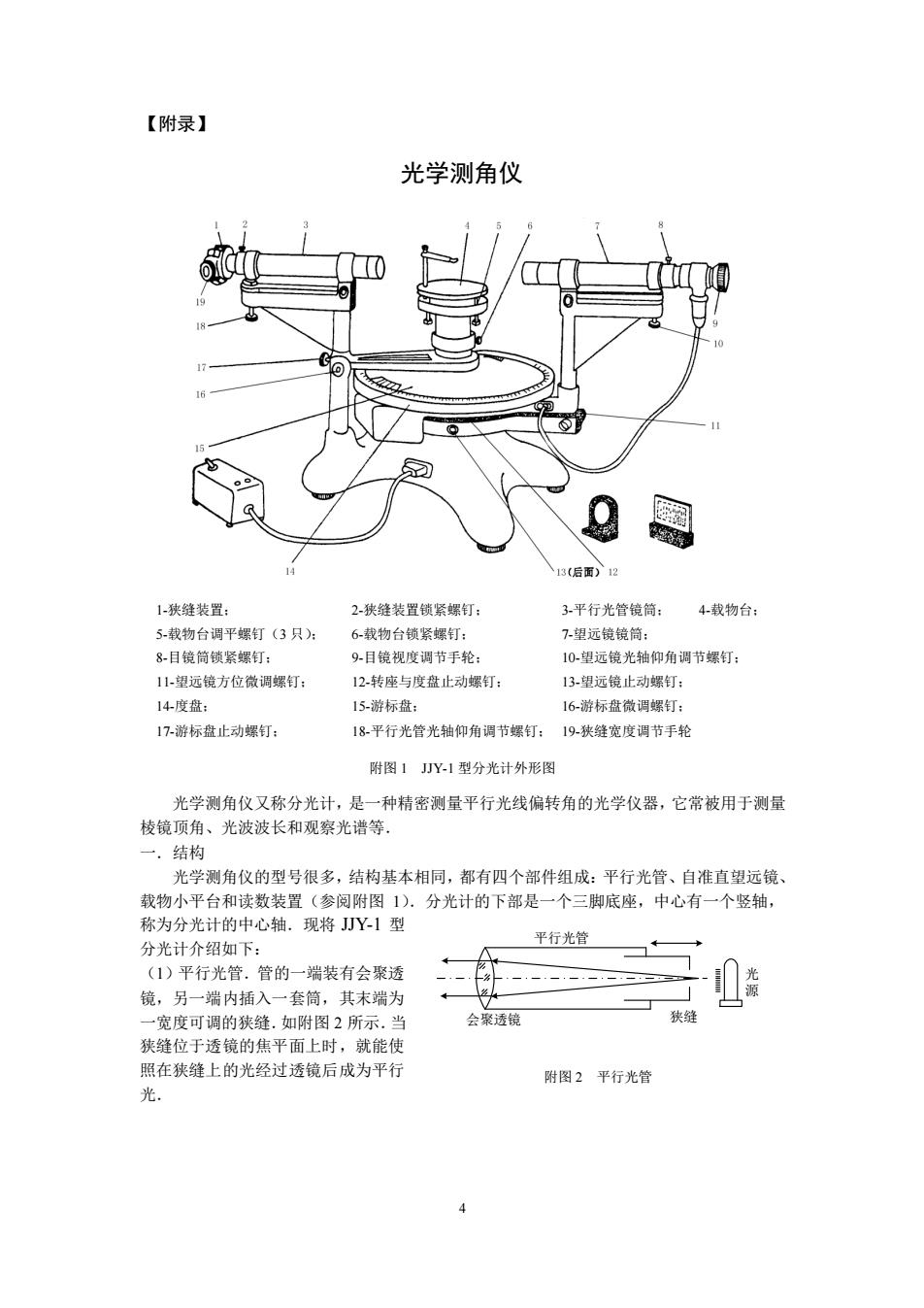
【附录】 光学测角仪 15 13(后面)12 1-狭缝装置: 2狭缝装置锁紧螺钉: 3平行光管镜筒: 4载物台: 5载物台调平螺钉(3只): 6载物台锁紧螺钉: 7-望远镜镜筒: 8-目镜筒锁紧螺钉: 9-目镜视度调节手轮: 10望远镜光轴仰角调节螺钉: 11望远镜方位微调螺钉: 12-转座与度盘止动螺钉: 13-望远镜止动螺钉: 14度盘: 15-游标盘: 16-游标盘微调螺钉: 17-游标盘止动螺钉: 18平行光管光轴仰角调节螺钉:19-狭缝宽度调节手轮 附图1JY-1型分光计外形图 光学测角仪又称分光计,是一种精密测量平行光线偏转角的光学仪器,它常被用于测量 棱镜顶角、光波波长和观察光谱等, 一.结构 光学测角仪的型号很多,结构基本相同,都有四个部件组成:平行光管、自准直望远镜、 载物小平台和读数装置(参阅附图1).分光计的下部是一个三脚底座,中心有一个竖轴, 称为分光计的中心轴.现将JJY-1型 平行光管 分光计介绍如下: (1)平行光管.管的一端装有会聚透 镜,另一端内插入一套筒,其末端为 一宽度可调的狭缝.如附图2所示.当 会聚透镜 狭缝 狭缝位于透镜的焦平面上时,就能使 照在狭缝上的光经过透镜后成为平行 附图2平行光管 光. 4
4 【附录】 光学测角仪 光学测角仪又称分光计,是一种精密测量平行光线偏转角的光学仪器,它常被用于测量 棱镜顶角、光波波长和观察光谱等. 一.结构 光学测角仪的型号很多,结构基本相同,都有四个部件组成:平行光管、自准直望远镜、 载物小平台和读数装置(参阅附图 1).分光计的下部是一个三脚底座,中心有一个竖轴, 称为分光计的中心轴.现将 JJY-1 型 分光计介绍如下: (1)平行光管.管的一端装有会聚透 镜,另一端内插入一套筒,其末端为 一宽度可调的狭缝.如附图 2 所示.当 狭缝位于透镜的焦平面上时,就能使 照在狭缝上的光经过透镜后成为平行 光. 光 源 会聚透镜 狭缝 平行光管 附图 2 平行光管 1-狭缝装置; 2-狭缝装置锁紧螺钉; 3-平行光管镜筒; 4-载物台; 5-载物台调平螺钉(3 只); 6-载物台锁紧螺钉; 7-望远镜镜筒; 8-目镜筒锁紧螺钉; 9-目镜视度调节手轮; 10-望远镜光轴仰角调节螺钉; 11-望远镜方位微调螺钉; 12-转座与度盘止动螺钉; 13-望远镜止动螺钉; 14-度盘; 15-游标盘; 16-游标盘微调螺钉; 17-游标盘止动螺钉; 18-平行光管光轴仰角调节螺钉; 19-狭缝宽度调节手轮 附图 1 JJY-1 型分光计外形图
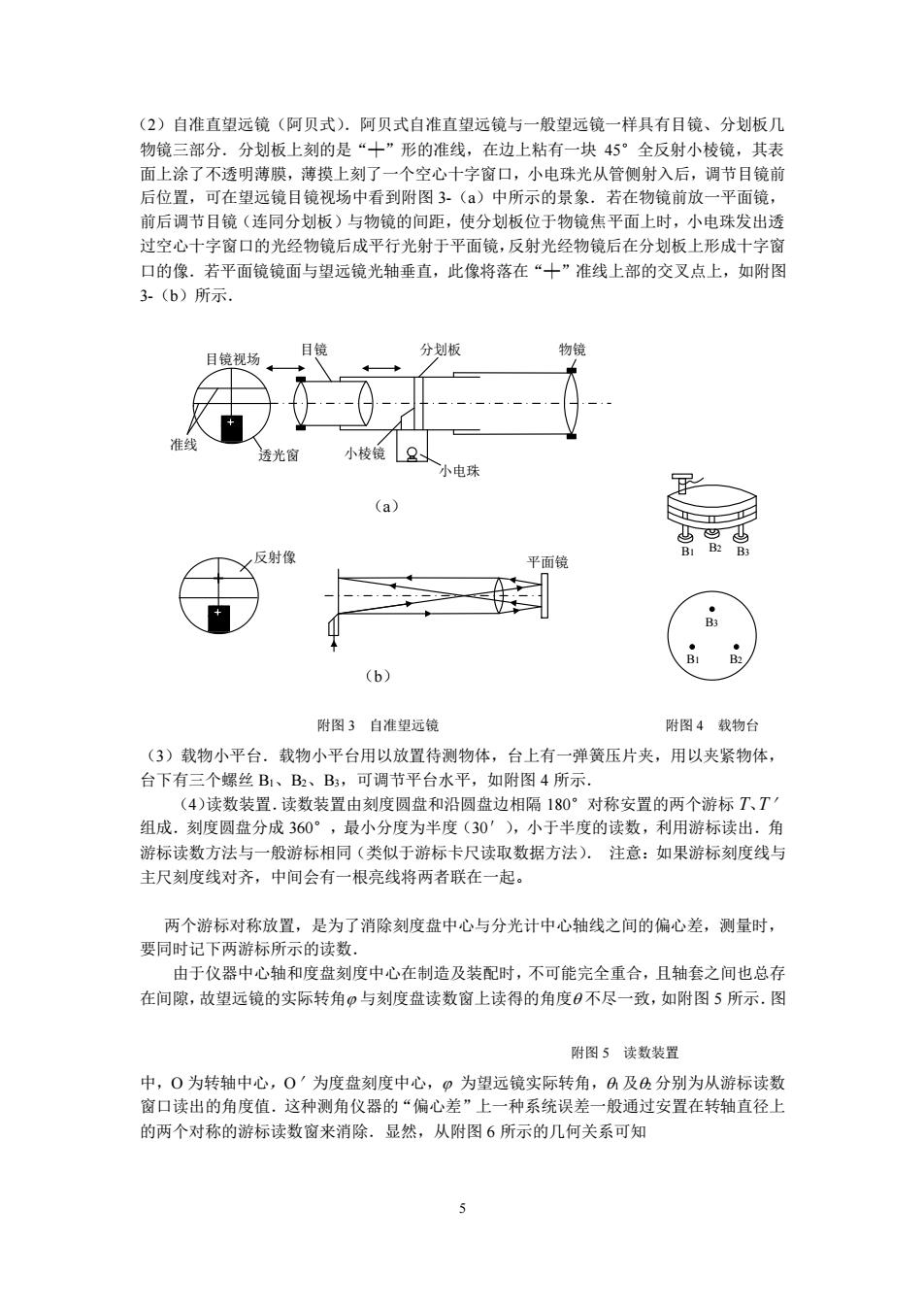
(2)自准直望远镜(阿贝式).阿贝式自准直望远镜与一般望远镜一样具有目镜、分划板几 物镜三部分.分划板上刻的是“十”形的准线,在边上粘有一块45°全反射小棱镜,其表 面上涂了不透明薄膜,薄摸上刻了一个空心十字窗口,小电珠光从管侧射入后,调节目镜前 后位置,可在望远镜目镜视场中看到附图3-()中所示的景象.若在物镜前放一平面镜, 前后调节目镜(连同分划板)与物镜的间距,使分划板位于物镜焦平面上时,小电珠发出透 过空心十字窗口的光经物镜后成平行光射于平面镜,反射光经物镜后在分划板上形成十字窗 口的像.若平面镜镜面与望远镜光轴垂直,此像将落在“十”准线上部的交叉点上,如附图 3-(b)所示. 目镜视场 目镜 分划板 物镜 准线 透光窗 小棱镜 小电珠 (a) 反射像 BI B2 B3 平面镜 B3 (b) 附图3自准望远镜 附图4载物台 (3)载物小平台.载物小平台用以放置待测物体,台上有一弹簧压片夹,用以夹紧物体, 台下有三个螺丝B1、B2、B3,可调节平台水平,如附图4所示. (4)读数装置.读数装置由刻度圆盘和沿圆盘边相隔180°对称安置的两个游标T、T‘ 组成.刻度圆盘分成360°,最小分度为半度(30'),小于半度的读数,利用游标读出.角 游标读数方法与一般游标相同(类似于游标卡尺读取数据方法).注意:如果游标刻度线与 主尺刻度线对齐,中间会有一根亮线将两者联在一起。 两个游标对称放置,是为了消除刻度盘中心与分光计中心轴线之间的偏心差,测量时, 要同时记下两游标所示的读数. 由于仪器中心轴和度盘刻度中心在制造及装配时,不可能完全重合,且轴套之间也总存 在间隙,故望远镜的实际转角0与刻度盘读数窗上读得的角度θ不尽一致,如附图5所示.图 附图5读数装置 中,0为转轴中心,0'为度盘刻度中心,0为望远镜实际转角,凸及凸分别为从游标读数 窗口读出的角度值.这种测角仪器的“偏心差”上一种系统误差一般通过安置在转轴直径上 的两个对称的游标读数窗来消除.显然,从附图6所示的几何关系可知 5
5 (2)自准直望远镜(阿贝式).阿贝式自准直望远镜与一般望远镜一样具有目镜、分划板几 物镜三部分.分划板上刻的是“╪”形的准线,在边上粘有一块 45°全反射小棱镜,其表 面上涂了不透明薄膜,薄摸上刻了一个空心十字窗口,小电珠光从管侧射入后,调节目镜前 后位置,可在望远镜目镜视场中看到附图 3-(a)中所示的景象.若在物镜前放一平面镜, 前后调节目镜(连同分划板)与物镜的间距,使分划板位于物镜焦平面上时,小电珠发出透 过空心十字窗口的光经物镜后成平行光射于平面镜,反射光经物镜后在分划板上形成十字窗 口的像.若平面镜镜面与望远镜光轴垂直,此像将落在“╪”准线上部的交叉点上,如附图 3-(b)所示. (3)载物小平台.载物小平台用以放置待测物体,台上有一弹簧压片夹,用以夹紧物体, 台下有三个螺丝 B1、B2、B3,可调节平台水平,如附图 4 所示. (4)读数装置.读数装置由刻度圆盘和沿圆盘边相隔 180°对称安置的两个游标 T、T′ 组成.刻度圆盘分成 360°,最小分度为半度(30′),小于半度的读数,利用游标读出.角 游标读数方法与一般游标相同(类似于游标卡尺读取数据方法). 注意:如果游标刻度线与 主尺刻度线对齐,中间会有一根亮线将两者联在一起。 两个游标对称放置,是为了消除刻度盘中心与分光计中心轴线之间的偏心差,测量时, 要同时记下两游标所示的读数. 由于仪器中心轴和度盘刻度中心在制造及装配时,不可能完全重合,且轴套之间也总存 在间隙,故望远镜的实际转角 与刻度盘读数窗上读得的角度 不尽一致,如附图 5 所示.图 中,O 为转轴中心,O′为度盘刻度中心, 为望远镜实际转角,1 及2 分别为从游标读数 窗口读出的角度值.这种测角仪器的“偏心差”上一种系统误差一般通过安置在转轴直径上 的两个对称的游标读数窗来消除.显然,从附图 6 所示的几何关系可知 目镜视场 目镜 分划板 物镜 小棱镜 小电珠 准线 透光窗 (a) 反射像 平面镜 (b) 附图 3 自准望远镜 B1 B2 B3 B1 B2 B3 附图 4 载物台 附图 5 读数装置

p+∠1=8+∠2, p叶∠2=凸+∠1, 两式相加得 20+(∠2+∠1)=8+&+(∠1+∠2) 故 2p=A+凸 p=g+8, 2 附图5偏心差的示意及消除 二.光学测角仪调整要求和方法 正式使用光学测角仪前,必须按下列程序进行调整: (1)望远镜和载物台粗调. 1、用眼晴从仪器侧面观察望远镜光轴、平行光管光轴平行,载物台面水平. 2、调节目镜,使得目镜视场中能清晰地看清“十”准线。 3、调节目镜(连同分划板)与物镜间距,使分划板位于物镜焦平面上,此时 视场中可同时看清“十”准线及“+”字反射像,(且使两者无视差)。 4、将双面镜放置在载物台上,其中一边对准一个底角螺丝,另外一边位于两 个螺丝之间。 5、转动载物台,双面镜两面反射的十字反射像均能看到。(不用管在何位置)。 (2)望远镜和载物台细调. 1、望远镜轴与中心轴是否垂直,可根据反射“+”字像是否位于“十”准线最 上面水平线上来判断。因为望远镜和载物台均可能不平,因此两者必须协同 调节。调节方法是“逐次逼近各半调节法”。 如附图6所示.由于调整时双面镜总是放在载物台上,因此只要转动载物台 使双面镜随同转动,反射“+”字像也将随着发生相应的移动.在双面镜旋 转180°前、后均能看到准线及“+”字反射像,但它们又相互错开的情况下, 即可先调节望远镜轴的仰角螺丝以消除错开距离的一半/2,而另一半则可 调节载物台位于双面镜两侧的螺丝来消除,使“+”字反射像落在“十”准 线的上交点上.反复进行调整直至载物台每转过180°,反射“+”字像都与 准线上部交点重合为止. 2、将载物台上双面镜转90度,只调节一直未动的,与双面镜对齐的螺丝,使 得反射“+”字像再次与准线上部交点重合.(其它螺丝包括望远镜仰角螺丝 都不要动)。此时即可认为望远镜光轴已垂直于中心轴了.固定望远镜倾斜 紧定螺丝,并以此作为以后调节其他部分的基准. (3)调整平行光管产生平行光。 1、首先从侧面和俯视两个方向用目测法把平行光管轴大致调节到与望远镜光轴 相一致: 2、从望远镜中进行观察狭缝像,松开平行光管上的狭缝锁紧螺钉,前后移动狭 缝,使得狭缝像清晰,此时狭缝位于透镜的焦平面上,产生平行光:调节平 6
6 +∠= 1+∠, +∠= 2+∠, 两式相加得 +(∠+∠)= 1+ 2+(∠+∠) 故 = 1+ 2 2 1 2 + = 二.光学测角仪调整要求和方法 正式使用光学测角仪前,必须按下列程序进行调整: (1) 望远镜和载物台粗调. 1、 用眼睛从仪器侧面观察望远镜光轴、平行光管光轴平行,载物台面水平. 2、 调节目镜,使得目镜视场中能清晰地看清“╪”准线。 3、 调节目镜(连同分划板)与物镜间距,使分划板位于物镜焦平面上,此时 视场中可同时看清“╪”准线及“+”字反射像,(且使两者无视差)。 4、 将双面镜放置在载物台上,其中一边对准一个底角螺丝,另外一边位于两 个螺丝之间。 5、 转动载物台,双面镜两面反射的十字反射像均能看到。(不用管在何位置)。 (2) 望远镜和载物台细调. 1、望远镜轴与中心轴是否垂直,可根据反射“+”字像是否位于“╪”准线最 上面水平线上来判断。因为望远镜和载物台均可能不平,因此两者必须协同 调节。调节方法是“逐次逼近各半调节法”。 如附图 6 所示.由于调整时双面镜总是放在载物台上,因此只要转动载物台 使双面镜随同转动,反射“+”字像也将随着发生相应的移动.在双面镜旋 转 180°前、后均能看到准线及“+”字反射像,但它们又相互错开的情况下, 即可先调节望远镜轴的仰角螺丝以消除错开距离的一半 h/2,而另一半则可 调节载物台位于双面镜两侧的螺丝来消除,使“+”字反射像落在“╪”准 线的上交点上.反复进行调整直至载物台每转过 180°,反射“+”字像都与 准线上部交点重合为止. 2、将载物台上双面镜转 90 度,只调节一直未动的,与双面镜对齐的螺丝,使 得反射“+”字像再次与准线上部交点重合.(其它螺丝包括望远镜仰角螺丝 都不要动)。此时即可认为望远镜光轴已垂直于中心轴了.固定望远镜倾斜 紧定螺丝,并以此作为以后调节其他部分的基准. (3)调整平行光管产生平行光。 1、首先从侧面和俯视两个方向用目测法把平行光管轴大致调节到与望远镜光轴 相一致: 2、从望远镜中进行观察狭缝像,松开平行光管上的狭缝锁紧螺钉,前后移动狭 缝,使得狭缝像清晰,此时狭缝位于透镜的焦平面上,产生平行光;调节平 T2 ′ T 1′ T2 T 1 1 2 O O′ θ1 θ2 1 2 附图 5 偏心差的示意及消除
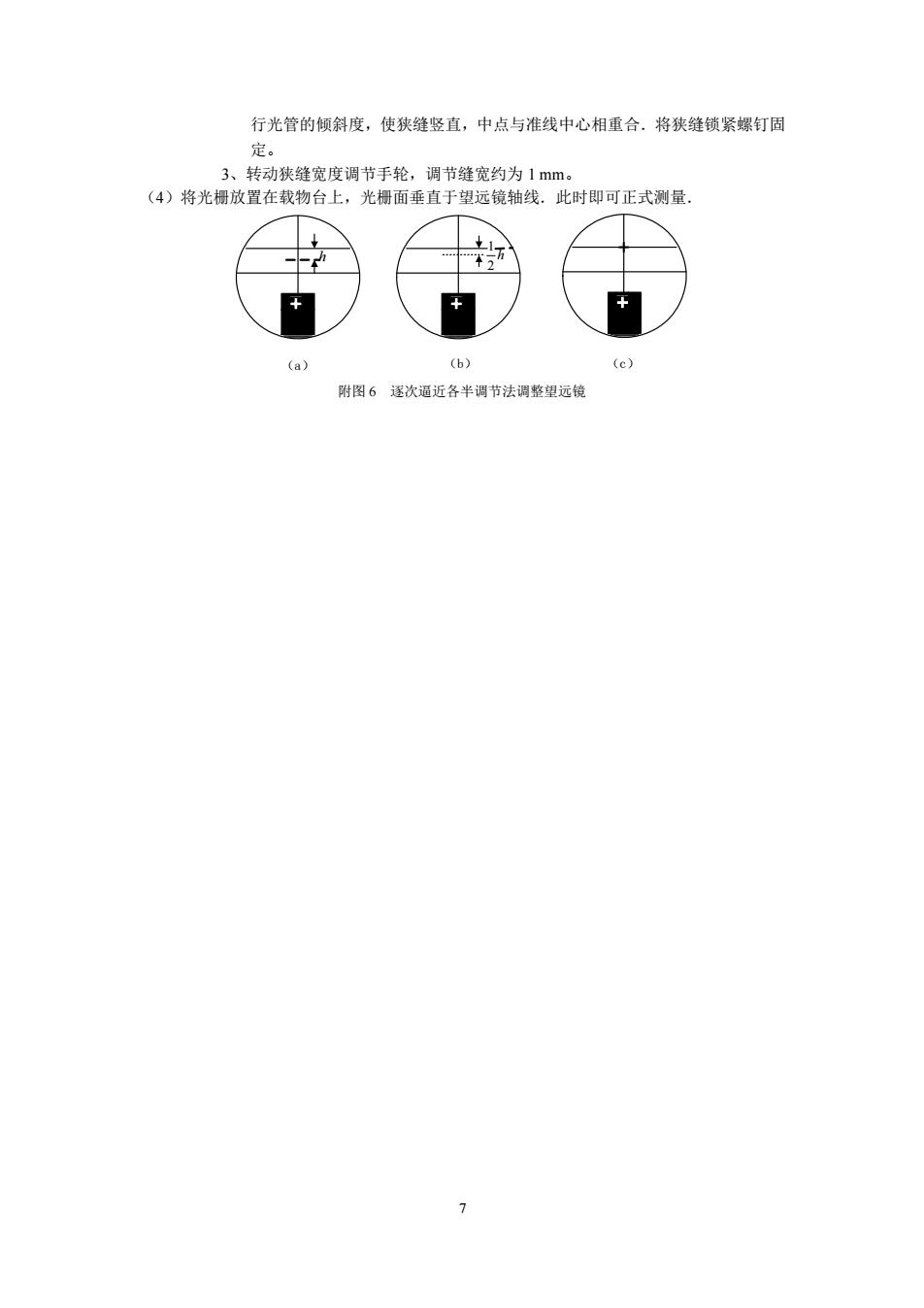
行光管的倾斜度,使狭缝竖直,中点与准线中心相重合,将狭缝锁紧螺钉固 定。 3、转动狭缝宽度调节手轮,调节缝宽约为1mm。 (4)将光柵放置在载物台上,光栅面垂直于望远镜轴线.此时即可正式测量. + (a) (b) (c) 附图6逐次逼近各半调节法调整望远镜 7
7 行光管的倾斜度,使狭缝竖直,中点与准线中心相重合.将狭缝锁紧螺钉固 定。 3、转动狭缝宽度调节手轮,调节缝宽约为 1 mm。 (4)将光栅放置在载物台上,光栅面垂直于望远镜轴线.此时即可正式测量. h (a) (b) (c) h 2 1 附图 6 逐次逼近各半调节法调整望远镜