
实验一PN结物理特性的测量 伏安特性是PN结的基本特性,测量PN结的扩散电流与PN结电压之间的关系,可以 验证它们遵守波尔兹曼分布,并进而求出波尔兹曼常数的值.PN结的扩散电流很小,为 106~I08A数量级,所以在测量PN结扩散电流的过程中,运用了弱电流测量技术,即用 运算放大器对电流进行电流-电压变换. 【实验目的】 1.学习利用运算放大器测量微小电流: 2.掌握PN结的伏安特性,学习曲线拟合方法,求出波尔兹曼常数. 【实验原理】 1.LF356运算放大器介绍 利用LF356运算放大器可以组成电流-电压 变换器,如图1所示.LF356运算放大器是一个 集成运算放大器,R为反馈电阻,若R→∞时, 输出电压U6与输入电压U,的比值叫做运算放大 器的开环增益K.运算放大器的输入阻抗”很 大,理想情况下r→·∞,可以认为反馈电流等 于信号源的输入电流I.Z为电流一电压变换器 的等效输入阻抗,因为反馈电流等于信号源的输 图1电流-电压变换电路 入电流1,输入电流I,可以写为 _U,-U。 I,=- (1) R 其中,U为运算放大器的输入电压,U。为运算放大器的输出电压,二者的关系为: Uo=-KoU; (2) 将(2)代入(1)得: 0,U=-00+ 1= (3) R 其中K运算放大器的开环电压放大倍数,一般为103~10°. 所以,如果测出U%,即可得到I,.我们选取反馈电阻Rr=1M2,用量程为200mV 的数字电压表,它的分辨率为0.01mV,则能测到的最小电流为 1,=0,01mY=1x10"A 1 MQ -1-
- 1 - 图 1 电流-电压变换电路 实验一 PN 结物理特性的测量 伏安特性是 PN 结的基本特性,测量 PN 结的扩散电流与 PN 结电压之间的关系,可以 验证它们遵守波尔兹曼分布,并进而求出波尔兹曼常数的值.PN 结的扩散电流很小,为 10-6~10-8 A 数量级,所以在测量 PN 结扩散电流的过程中,运用了弱电流测量技术,即用 运算放大器对电流进行电流-电压变换. 【实验目的】 1.学习利用运算放大器测量微小电流; 2.掌握 PN 结的伏安特性,学习曲线拟合方法,求出波尔兹曼常数. 【实验原理】 1.LF356 运算放大器介绍 利用LF356运算放大器可以组成电流-电压 变换器,如图 1 所示.LF356 运算放大器是一个 集成运算放大器,Rf为反馈电阻,若 Rf→ ∞时, 输出电压U0与输入电压Ui的比值叫做运算放大 器的开环增益 K0.运算放大器的输入阻抗 r 很 大,理想情况下 r → ∞,可以认为反馈电流等 于信号源的输入电流 Is.Zr为电流—电压变换器 的等效输入阻抗,因为反馈电流等于信号源的输 入电流 Is,输入电流 Is可以写为 f i s R U U I - 0 = (1) 其中,Ui为运算放大器的输入电压,U0为运算放大器的输出电压,二者的关系为: U0 = -K0Ui (2) 将(2)代入(1)得: f f f i s R U R K U R U U I 0 0 0 0 ) 1 = - (1+ » - - = (3) 其中 K0 运算放大器的开环电压放大倍数,一般为 105~106. 所以,如果测出 U0,即可得到 Is.我们选取反馈电阻 R f = 1 MW ,用量程为 200 mV 的数字电压表,它的分辨率为 0.01 mV,则能测到的最小电流为 1 10 A 1 MΩ 0.01 mV -11 I s = = ´

由此可见,电流-电压变换器具有很高的灵敏度, 2.PN结的伏安特性 从固体理论可知,理想PN结的正向电流-电压关系满足下式 (4) 其中,I是通过PN结的正向电流,。是反向饱和电流(与半导体的性质和掺杂有关),U 是加在PN结上的正向电压,T为绝对温度,ks为波尔兹曼常数,e为基本电荷量.常温下, e/kgT≈38,exp(eU/kgT)>l,(1)式可以近似写成 I=Iexpl (5) kaT 在常温下,PN结的正向电流随正向电压按e指数规律变化,电压很小时,电流很小, 需要用电流一电压变换器测量电流.如果测量得到PN结的伏安特性,即可验证上述规律.测 量得到温度T后,利用基本电荷值,可求得波尔兹曼常数k®.将(2)式两边取对数,得 lnl=lnl。+ el (6) kgT 分别以U和lnl为变量,作线性最小二乘法拟合,得到e/kT,可以得到ka.实验中 (见图3),U为U山,I=U2/R,(6)式变为 nL=hl,+nR,)+e吗 (7) kgT 用U1为横坐标,nU2为纵坐标拟合即可. 在实验中,如果利用二极管进行测量,往往得不到好的结果,其原因是:()存在耗 尽层电流,其值正比于exp(eU/2kgT):(b)存在表面电流,其值正比于exp(eU/mkgT), m>2. 为了不受上述影响,一般不用二极管,而是采用三极管接成共基极电路,集电极与基 极短接.复合电流主要在基极出现,集电极中主要是扩散电流,如果选择好的三极管,表 面电流也可以忽略,此时集电极电流与基极、发射极电压满足(2)式.本实验选择TP31 型硅三极管. 【实验仪器】 ±15V直流稳压电源,TIP31型硅三极管,LF356集成运算放大器,四位半数字万用 表,电阻,电容,电位器,导线,实验接线板等. TIP31型硅三极管,LF356集成运算放大器的管脚如图2所示. -2-
- 2 - 由此可见,电流-电压变换器具有很高的灵敏度. 2.PN 结的伏安特性 从固体理论可知,理想 PN 结的正向电流-电压关系满足下式 ú ú û ù ê ê ë é - ÷ ÷ ø ö ç ç è æ = exp 1 0 k T eU I I B (4) 其中,I 是通过 PN 结的正向电流,I0 是反向饱和电流(与半导体的性质和掺杂有关),U 是加在 PN 结上的正向电压,T 为绝对温度,kB为波尔兹曼常数,e 为基本电荷量.常温下, e / kBT ≈38,exp (eU / kBT ) >>1,(1)式可以近似写成 ÷ ÷ ø ö ç ç è æ = k T eU I I B 0 exp (5) 在常温下,PN 结的正向电流随正向电压按 e 指数规律变化,电压很小时,电流很小, 需要用电流-电压变换器测量电流.如果测量得到 PN结的伏安特性,即可验证上述规律.测 量得到温度 T 后,利用基本电荷值,可求得波尔兹曼常数 kB.将(2)式两边取对数,得 k T eU I I B ln = ln 0 + (6) 分别以 U 和 lnI 为变量,作线性最小二乘法拟合,得到 e / kBT,可以得到 kB.实验中 (见图 3),U 为 U1 ,I = U2 / R f ,(6)式变为 k T eU U I R B f 1 2 0 ln = (ln + ln ) + (7) 用 U1为横坐标,lnU2为纵坐标拟合即可. 在实验中,如果利用二极管进行测量,往往得不到好的结果,其原因是:(a)存在耗 尽层电流,其值正比于 exp(eU / 2kBT);(b)存在表面电流,其值正比于 exp(eU / mkBT), m > 2. 为了不受上述影响,一般不用二极管,而是采用三极管接成共基极电路,集电极与基 极短接.复合电流主要在基极出现,集电极中主要是扩散电流,如果选择好的三极管,表 面电流也可以忽略,此时集电极电流与基极、发射极电压满足(2)式.本实验选择 TIP31 型硅三极管. 【实验仪器】 ±15V 直流稳压电源,TIP31 型硅三极管,LF356 集成运算放大器,四位半数字万用 表,电阻,电容,电位器,导线,实验接线板等. TIP31 型硅三极管,LF356 集成运算放大器的管脚如图 2 所示.
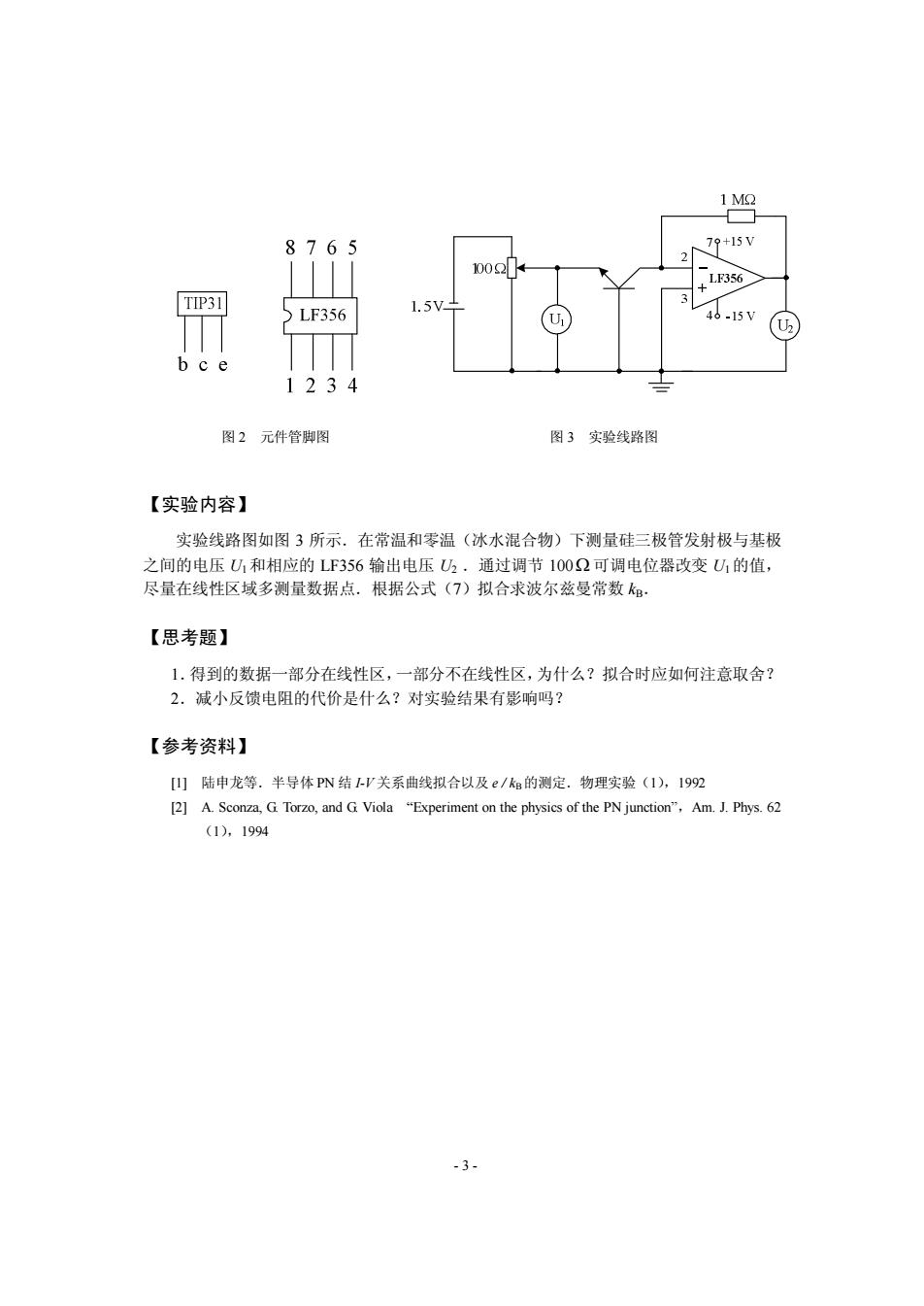
1M2 8765 79+15V 2 1002← LF356> TIP31 3 LF356 1.5V 4o-15V b c e 1234 图2元件管脚图 图3实验线路图 【实验内容】 实验线路图如图3所示.在常温和零温(冰水混合物)下测量硅三极管发射极与基极 之间的电压U1和相应的LF356输出电压U2.通过调节1002可调电位器改变U1的值, 尽量在线性区域多测量数据点.根据公式(7)拟合求波尔兹曼常数: 【思考题】 1.得到的数据一部分在线性区,一部分不在线性区,为什么?拟合时应如何注意取舍? 2.减小反馈电阻的代价是什么?对实验结果有影响吗? 【参考资料】 山陆申龙等.半导体PN结I-V关系曲线拟合以及e/k的测定.物理实验(1),192 [2]A.Sconza,G Torzo,and G Viola "Experiment on the physics of the PN junction",Am.J.Phys.62 (1),1994 -3-
- 3 - 图 3 实验线路图 【实验内容】 实验线路图如图 3 所示.在常温和零温(冰水混合物)下测量硅三极管发射极与基极 之间的电压 U1和相应的 LF356 输出电压 U2 .通过调节 100W 可调电位器改变 U1的值, 尽量在线性区域多测量数据点.根据公式(7)拟合求波尔兹曼常数 kB. 【思考题】 1.得到的数据一部分在线性区,一部分不在线性区,为什么?拟合时应如何注意取舍? 2.减小反馈电阻的代价是什么?对实验结果有影响吗? 【参考资料】 [1] 陆申龙等.半导体 PN 结 I-V 关系曲线拟合以及 e / kB的测定.物理实验(1),1992 [2] A. Sconza, G. Torzo, and G. Viola “Experiment on the physics of the PN junction”,Am. J. Phys. 62 (1),1994 图 2 元件管脚图