傅立叶综合器组合实验 引言 在数学上,任何一个周期性的波均可分解成一无穷数列的三角函数之和来表示,三角函 数是由正弦或余弦表示的谐波。利用该仪器(PASCO WA-9307A)可以证明和观察这种数学 模型,将一系列的正弦波相加,可以在示波器上观察其结果。 仪器介绍 1.傅立叶分析仪(如图1) HARMONICS 2nd 4th 6th 880H 3rd (1760Ht) 5th 2640H7h 9 (1320H) 2200Hz 3080H0 3980H 中 中 中· 白 包 中 中 中 @ 图1 本仪器提供10组谐振波,频率分别为440Hz(有2个)880HZ,1320HZ,1760HZ,2200HZ, 2640HZ,3080HZ,3520HZ,3960HZ,分别呈倍数递增,将傅立叶分析仪与示波器相连, 如图2。每一个谐波的输出均通过控制键,如图3来控制,其中基频波除谐波外,还有另外 两种附加的波形,分别是三角波和方波,通过两个按钮来选取,每一个波均可调节振幅和相 位的大小。 0 k OUTPUT (Individual Harmonics 1 of 10): Connect to input of oscilloscope to view waveform (channel 2). Speaker Jacks nnec speake 82 input impedance】 TRIGGER OUTPUT:Connect to external 10 k OUTPUT (Summing mg8eictpes ope has cope (or to Sync if your Amplifier)-Connect to input of no extemal trigge)) oscilloscope (channel 1) Ground Jacks:Connect one to the ground of the oscilloscope 图2 注意三点: (1)本仪器在使用之前,应将仪器各旋钮置于”0”状态,这个初始状态是指0一90
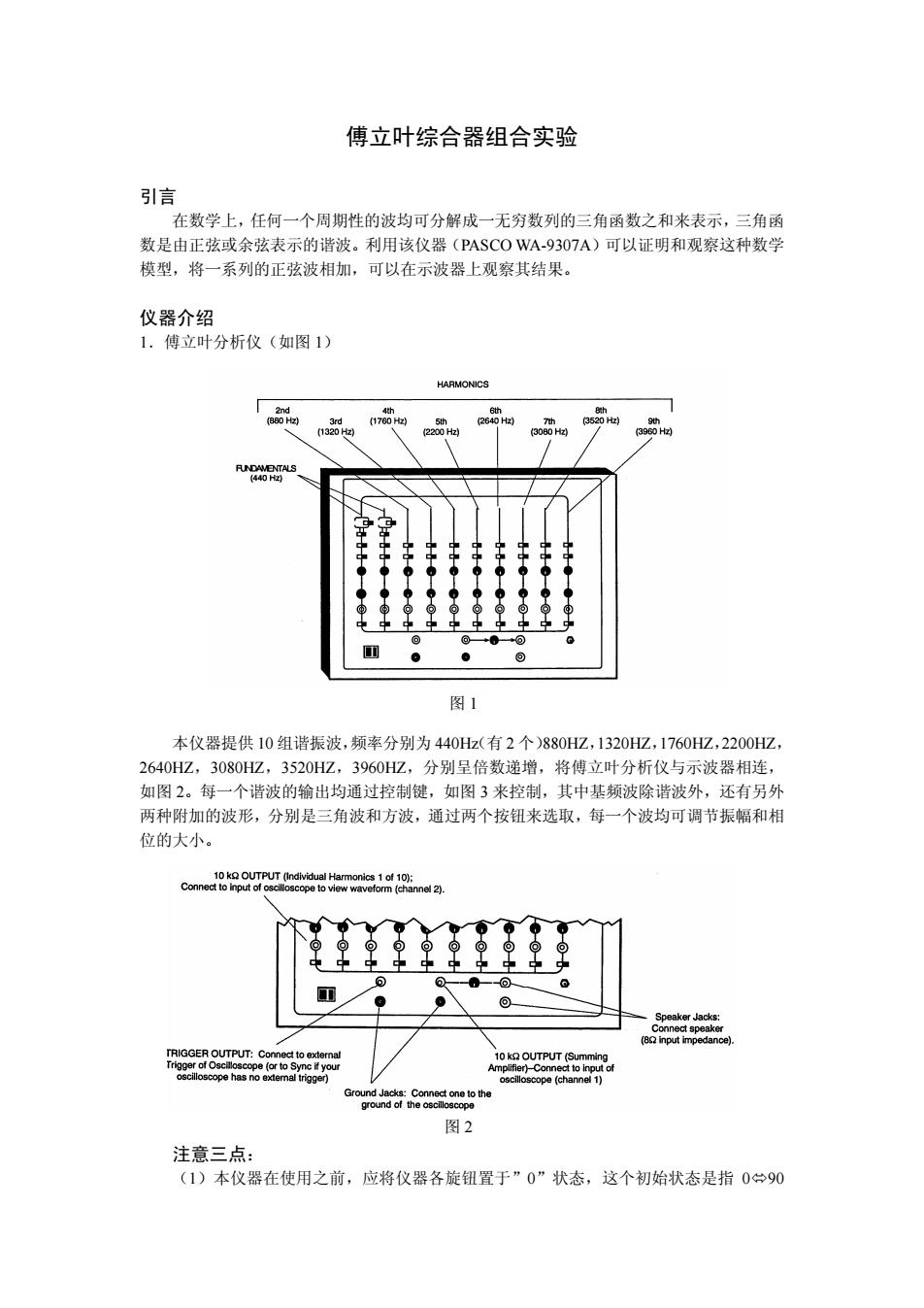
傅立叶综合器组合实验 引言 在数学上,任何一个周期性的波均可分解成一无穷数列的三角函数之和来表示,三角函 数是由正弦或余弦表示的谐波。利用该仪器(PASCO WA-9307A)可以证明和观察这种数学 模型,将一系列的正弦波相加,可以在示波器上观察其结果。 仪器介绍 1.傅立叶分析仪(如图 1) 图 1 本仪器提供 10 组谐振波,频率分别为 440Hz(有 2 个)880HZ,1320HZ,1760HZ,2200HZ, 2640HZ,3080HZ,3520HZ,3960HZ,分别呈倍数递增,将傅立叶分析仪与示波器相连, 如图 2。每一个谐波的输出均通过控制键,如图 3 来控制,其中基频波除谐波外,还有另外 两种附加的波形,分别是三角波和方波,通过两个按钮来选取,每一个波均可调节振幅和相 位的大小。 图 2 注意三点: (1)本仪器在使用之前,应将仪器各旋钮置于”0”状态,这个初始状态是指 0Ù90

及0180拨于0,将叠加合成器置于”OUT”,另外要随时按下复位键(RESET): Switch to seledt square of triangular waveform (fundamentals only) Switch to select sine wave or square/triangular wave option(fundamentals onty) 0180:Switch to adjust phase of waveform by exactly 180 90:Switch to adjust phase of waveform by exactly 90 VARIABLE PHASE:Turn to adust phase of wavefom(90 range) AMPLITUDE:Tum to adjst the amplitude of the waveform 10 ks2 Output:Connect to oscilloscope to view waveform SUMMING AMPLIFIER: IN-Switches harmonic into summed output. ■ OUT-Switches harmonic out of summed output. 图3 (2)将基频波接入叠加合成器上的"N”,利用示波器上的扫描,检查傅立叶分析仪的输 出端的信号确立扫描的初始相位(0点)调节水平轴,以便看到分析仪的输出的正 弦波或余弦波叠加合成器常会产生180的相移,故要经常用0一180的按钮来校正, 同时用RESET键来复位。使被形回复到初始状态。 2.示波器 示波器带有外触发的双迹示波器对于本实验是必需的,外触发是能提供给各个输入波形 一个可参考的固定相位的波,这样可以方便地比较单个波的相位,以及合成后的相位。双迹 是可以用其中之一来观察初始波形,另一个观察叠加合成后的波形
及 0Ù180 拨于 0,将叠加合成器置于”OUT”,另外要随时按下复位键(RESET); 图 3 (2) 将基频波接入叠加合成器上的"IN”,利用示波器上的扫描,检查傅立叶分析仪的输 出端的信号确立扫描的初始相位(0 点)调节水平轴,以便看到分析仪的输出的正 弦波或余弦波叠加合成器常会产生 180 的相移,故要经常用 0Ù180 的按钮来校正, 同时用 RESET 键来复位。使波形回复到初始状态。 2.示波器 示波器带有外触发的双迹示波器对于本实验是必需的,外触发是能提供给各个输入波形 一个可参考的固定相位的波,这样可以方便地比较单个波的相位,以及合成后的相位。双迹 是可以用其中之一来观察初始波形,另一个观察叠加合成后的波形

实验1同频率的正弦波的叠加 实验原理 当相同频率的谐波叠加时,仍然得到相同频率的谐振波而对于方波和三角波则不然。 实验内容 1.将示波器与傅立叶分析相接,如观察叠加合成波,应使示波器与此10K的输出端口相 连、显示波形置于外触发的输出状态: 2.将第一个基频信号接入叠加合成器,使之处于“N”位置,而将第二个基频信号及其 它谐波置于“OUT”状态。选择正弦波输出来操作。调节振幅旋钮于合适的大小,以 接近最大值(即1ⅴ大小的峰值较为适当)。调节示波器上的垂直增益,使正弦波的峰值 小于或等于显示信号的一半(通常0.5v/格较合适)。调节0一90及0一180键和可变 相位控制钮来显示正弦或余弦波。将第一个基频信号置于OUT,而第二个基频信号置 于“N”。调节控制钮使第二个信号产生的正弦波与第一个信号的大小及相位完全一致: 3.然后再将第一个调好的基频信号也输入叠加合成器中,二者合成的波是否仍是正弦波? 叠加合成的波的大小及相位与两个初始波的大小及相位有什么关系? 4. 改变其中一个波的大小,再看一看合成波的大小及相位的变化: 5.改变其中一个波被的相位。首先选用可变相位钮调节,然后用0一90,0一180来检查合 成波的大小及相位的变化: 6.什么条件下,可使合成波得到振幅为最大值及最小值? 7.将两个初级波换成三角及方波,再重复上述过程(此时应注意,调节相位钮对方波和三 角不起作用): 8.最后观察方波与正弦波的叠加、方波与三角波的叠加,以及三角形与正弦波的叠加的波 形,并作记录和分折
实验 1 同频率的正弦波的叠加 实验原理 当相同频率的谐波叠加时,仍然得到相同频率的谐振波而对于方波和三角波则不然。 实验内容 1. 将示波器与傅立叶分析相接,如观察叠加合成波,应使示波器与此 10K 的输出端口相 连、显示波形置于外触发的输出状态; 2. 将第一个基频信号接入叠加合成器,使之处于“IN”位置,而将第二个基频信号及其 它谐波置于“OUT”状态。选择正弦波输出来操作。调节振幅旋钮于合适的大小,以 接近最大值(即 1v 大小的峰值较为适当)。调节示波器上的垂直增益,使正弦波的峰值 小于或等于显示信号的一半(通常 0.5v/格较合适)。调节 0Ù90 及 0Ù180 键和可变 相位控制钮来显示正弦或余弦波。将第一个基频信号置于 OUT,而第二个基频信号置 于“IN”。调节控制钮使第二个信号产生的正弦波与第一个信号的大小及相位完全一致; 3. 然后再将第一个调好的基频信号也输入叠加合成器中,二者合成的波是否仍是正弦波? 叠加合成的波的大小及相位与两个初始波的大小及相位有什么关系? 4. 改变其中一个波的大小,再看一看合成波的大小及相位的变化; 5. 改变其中一个波的相位。首先选用可变相位钮调节,然后用 0Ù90,0Ù180 来检查合 成波的大小及相位的变化; 6. 什么条件下,可使合成波得到振幅为最大值及最小值? 7. 将两个初级波换成三角及方波,再重复上述过程(此时应注意,调节相位钮对方波和三 角不起作用); 8. 最后观察方波与正弦波的叠加、方波与三角波的叠加,以及三角形与正弦波的叠加的波 形,并作记录和分折

实验2不同频率的正弦波的叠加 实验原理 当振幅相同,但频率,2不同的正弦波叠加有如下关系 sin2at)+sin(2a'2t)=2cosπy1-v2t·sinπ(y1+v2)M 当,与2相差很大时,叠加波的观察是比较困难的,当y1与2很接近时,叠加波可以看 成是频率为当+之的正弦波,幅度的大小的变化(即包络波)随着频率为一之的波慢 2 慢调制。 实验内容 1.连接好傅立叶分析仪与示波器,选择第九个谐波作为叠加波的一个: 2.将第八个谐波接人叠加合成器中,使其它波断开,同时检查第七个及第八个谐波(用 0一180同时拨置观察相位的变化),描述叠加合成的结果。此时能看到节拍吗?如果能, 那么节拍的拍频是什么?调制波的频率是多大? 3. 改变其中一个波的振幅及相位再描述合成波的变化。 4.选择频率的不同组合方式,重复上述步骤,分析观察到的现象,如频率、节拍的变化。 5.从上述观察中,总结不同的频率的正弦波的叠加产生的结果,在什么情况下,可得到节 拍?
实验 2 不同频率的正弦波的叠加 实验原理 当振幅相同,但频率v1,v2不同的正弦波叠加有如下关系 ()( )tvtv ( ) ( )tvvtvv 1 2 21 21 π + π = cos22sin2sin π − ⋅sinπ + 当v1与v2相差很大时,叠加波的观察是比较困难的,当v1与v2很接近时,叠加波可以看 成是频率为 2 21 + vv 的正弦波,幅度的大小的变化(即包络波)随着频率为 2 21 − vv 的波慢 慢调制。 实验内容 1. 连接好傅立叶分析仪与示波器,选择第九个谐波作为叠加波的一个; 2. 将第八个谐波接人叠加合成器中,使其它波断开,同时检查第七个及第八个谐波(用 0Ùl80 同时拨置观察相位的变化),描述叠加合成的结果。此时能看到节拍吗?如果能, 那么节拍的拍频是什么?调制波的频率是多大? 3. 改变其中一个波的振幅及相位再描述合成波的变化。 4. 选择频率的不同组合方式,重复上述步骤,分析观察到的现象,如频率、节拍的变化。 5. 从上述观察中,总结不同的频率的正弦波的叠加产生的结果,在什么情况下,可得到节 拍?

实验3傅立叶分析 实验原理 约瑟夫·傅立叶发现任一周期性的函数可以表述成一无限正弦(或余弦)函数的级数之 和。在这个级数中,每一项的频率都是某一固定频率的倍数,利用傅立叶级数,任何周期运 动都可看成谐振动的叠加而成的,因此分析这类现象有了强有力的工具。本实验中,不同频 率的正弦波叠加合成为不同类型的波。 实验内容 1. 连续示波器与傅立叶分析仪,同上: 2.将傅立叶分析仪调”0”,将谐波的相位0°调好; 3.合成方波法: A将基频波接入叠加合成器中,调节振幅至尽可能大,井调节水平扫描使示波器看到清晰 的余弦函数。 B.关掉基频波,并接入第3个谐波调节它的大小至基频波的1/3并移相180使之看起来像 负的余弦波。 C.关掉第三个谐波,并接入第5个谐波调节它的大小至基频波的1/5,相位与基频波的相 同。 D.关掉第5个谐波,并接入第7个谐波调节它的大小至基频波的1/7并移相180使之是一 负的余弦波。 E.关掉第7个谐波,并接入第9个谐波调节它的大小至基频波的1/9,其相位不变。 F.将调节好的上述谐波都接入叠加合成器中(即都拨向“N”),观察每个谐波叠加后,合 成波的变化,最终得到一个方法,如要得到更好的方法,需叠加无穷级数的谐波。 4 其它波的合成,如下表格中,其振幅是用百分比表示,括号中的角度表示移相的大小, 合成方法与上述合成方法相似。 谐波分量 波形 1* 2 4 6 个 6 9 方波 100 0 33 20 0 14 0 11 (0) (180 (0 (180 (0) 三角波 100 0 11 0 4 0 0 1.2 (0) (0 (0 (0 (0% 锯齿波 100 50 33 25 20 17 12.5 11 (90° (270) (90 (270) (90) (270) (90) (270) (90 正弦波 100 33 8.3 4.8 3.3 2.1 1.3 1.2 0.9 (0 (180) (0 (180) (0) (180) (0) (180 (0) 抛物线 100 25 11 6.7 4 3 2 1.5 1.2 (0 (0 (0 (0 (0 (0 (0 (0) (0 *基本波形(440Hz)
实验 3 傅立叶分析 实验原理 约瑟夫·傅立叶发现任一周期性的函数可以表述成一无限正弦(或余弦)函数的级数之 和。在这个级数中,每一项的频率都是某一固定频率的倍数,利用傅立叶级数,任何周期运 动都可看成谐振动的叠加而成的,因此分析这类现象有了强有力的工具。本实验中,不同频 率的正弦波叠加合成为不同类型的波。 实验内容 1. 连续示波器与傅立叶分析仪,同上; 2. 将傅立叶分析仪调”0”,将谐波的相位 0º 调好; 3. 合成方波法: A.将基频波接入叠加合成器中,调节振幅至尽可能大,井调节水平扫描使示波器看到清晰 的余弦函数。 B.关掉基频波,并接入第 3 个谐波调节它的大小至基频波的 1/3 并移相 180 使之看起来像 负的余弦波。 C.关掉第三个谐波,并接入第 5 个谐波调节它的大小至基频波的 1/5,相位与基频波的相 同。 D.关掉第 5 个谐波,并接入第 7 个谐波调节它的大小至基频波的 1/7 并移相 180 使之是一 负的余弦波。 E.关掉第 7 个谐波,并接入第 9 个谐波调节它的大小至基频波的 1/9,其相位不变。 F. 将调节好的上述谐波都接入叠加合成器中(即都拨向“IN”),观察每个谐波叠加后,合 成波的变化,最终得到一个方法,如要得到更好的方法,需叠加无穷级数的谐波。 4 其它波的合成,如下表格中,其振幅是用百分比表示,括号中的角度表示移相的大小, 合成方法与上述合成方法相似。 谐波分量 波形 1* 2 3 4 5 6 7 8 9 方波 100 (0o ) 0 33 (180o ) 0 20 (0o ) 0 14 (180o ) 0 11 (0o ) 三角波 100 (0o ) 0 11 (0o ) 0 4 (0o ) 0 2 (0o ) 0 1.2 (0o ) 锯齿波 100 (90o ) 50 (270o ) 33 (90o ) 25 (270o ) 20 (90o ) 17 (270o ) 14 (90o ) 12.5 (270o ) 11 (90o ) 正弦波 100 (0o ) 33 (180o ) 8.3 (0o ) 4.8 (180o ) 3.3 (0o ) 2.1 (180o ) 1.3 (0o ) 1.2 (180o ) 0.9 (0o ) 抛物线 100 (0o ) 25 (0o ) 11 (0o ) 6.7 (0o ) 4 (0o ) 3 (0o ) 2 (0o ) 1.5 (0o ) 1.2 (0o ) * 基本波形(440Hz)

实验4吉布斯现象 实验原理 在傅立叶分布、谐波数列叠加合成时,会产生尖锐不连续的区间,好比方波的下降及上 升,这就是吉布斯现象,这种现象产生的不仅与谐波的叠加合成的数量有关,而且其变化的 宽度随合成的个数增加而变窄。 实验内容 重复实验3,分别一个个加上谐波,看看尖峰(或谷)的个数的变化及宽度的变化
实验 4 吉布斯现象 实验原理 在傅立叶分布、谐波数列叠加合成时,会产生尖锐不连续的区间,好比方波的下降及上 升,这就是吉布斯现象,这种现象产生的不仅与谐波的叠加合成的数量有关,而且其变化的 宽度随合成的个数增加而变窄。 实验内容 重复实验 3,分别一个个加上谐波,看看尖峰(或谷)的个数的变化及宽度的变化
实验5音乐 实验原理 有周期性变化的音乐就是一种复杂的周期波,音乐常用三个述语:音律,音量及音质来 表示音调,音带(Pitch):指音调变化的频率,高频产生高的音带。音量Loudness):指音 波的幅度,而音质(Quality)则是较复杂的现象,象口哨和钢琴能产生相同音带及音量的声音, 但这两音调完全不同,其原因是音乐音调是由某一相当幅度的基频组成的它确定音带,还有 较小幅度的较高频率的谐振,它决定音调的音质,这些较高的频率和相对的幅度我们在不同 乐器演奏同一音调的声音。 实验内容 1.将示波器与傅立叶分析相连,井将喇叭接好。 2.将第1基频波接入叠加合成器中调节波的大小,使在示波器看到合适的大小,并调节分析 仪的GAN按钮来改变音量。 3.接通方波并调节幅度,使之等于正弦波。接向三角波,让开关在这三种波中来回拨弄。 描述三种音调之间的Pitch、Loudness及Quality有什么不同,并分析听到的不同与示彼 器上看成的波形有何关系? 4.开关接向正弦波,比较基频率波与第2谐波的音调不同,通过幅度的变化及位相的变化, 看看有何影响。 5.接通更高的频率的谐波,改变幅度大小,分析示波器看到的波形变化与音乐的Pitch、 Loudness及Quality有什么关系? 6. 如下表格表示,小提琴,口哨及钢琴不同音调的谐波构成,据此合成不同的音调如何? 谐波分量 波形 1* 2 3 4 5 6 7 8 9 小提琴100 0 33 0 20 0 14 0 11 口哨 100 0 11 0 4 0 2 0 1.2 钢琴 100 50 33 25 20 17 14 12.5 11 *基本波形(440Hz) 实验6李萨如图 实验原理 将一谐波接人X轴,另一谐波接入Y轴只要两波的频率是成整数比,则可看到稳定的 李萨如图。 实验内容 1.将基频波接入示波器的X轴,同时将基频率接入示波器的Y轴,看李萨如图的变化? 2.将不同频率分别接入X、Y轴,调节幅度的大小,以及位相,看李萨如图如何变化?
实验 5 音乐 实验原理 有周期性变化的音乐就是一种复杂的周期波,音乐常用三个述语:音律,音量及音质来 表示音调,音带(Pitch):指音调变化的频率,高频产生高的音带。音量(Loudness):指音 波的幅度,而音质(Quality)则是较复杂的现象,象口哨和钢琴能产生相同音带及音量的声音, 但这两音调完全不同,其原因是音乐音调是由某一相当幅度的基频组成的它确定音带,还有 较小幅度的较高频率的谐振,它决定音调的音质,这些较高的频率和相对的幅度我们在不同 乐器演奏同一音调的声音。 实验内容 1. 将示波器与傅立叶分析相连,井将喇叭接好。 2. 将第 1 基频波接入叠加合成器中调节波的大小,使在示波器看到合适的大小,并调节分析 仪的 GAIN 按钮来改变音量。 3. 接通方波并调节幅度,使之等于正弦波。接向三角波,让开关在这三种波中来回拨弄。 描述三种音调之间的 Pitch、Loudness 及 Quality 有什么不同,并分析听到的不同与示彼 器上看成的波形有何关系? 4. 开关接向正弦波,比较基频率波与第 2 谐波的音调不同,通过幅度的变化及位相的变化, 看看有何影响。 5. 接通更高的频率的谐波,改变幅度大小,分析示波器看到的波形变化与音乐的 Pitch、 Loudness 及 Quality 有什么关系? 6. 如下表格表示,小提琴,口哨及钢琴不同音调的谐波构成,据此合成不同的音调如何? 谐波分量 波形 1* 2 3 4 5 6 7 8 9 小提琴 100 0 33 0 20 0 14 0 11 口哨 100 0 11 0 4 0 2 0 1.2 钢琴 100 50 33 25 20 17 14 12.5 11 * 基本波形(440Hz) 实验 6 李萨如图 实验原理 将一谐波接人 X 轴,另一谐波接入 Y 轴只要两波的频率是成整数比,则可看到稳定的 李萨如图。 实验内容 1.将基频波接入示波器的 X 轴,同时将基频率接入示波器的 Y 轴,看李萨如图的变化? 2.将不同频率分别接入 X、Y 轴,调节幅度的大小,以及位相,看李萨如图如何变化?